基于自适应模糊算法的四足机器人运动VMC方法

眭耀宇，杨忠，游雨龙，许昌亮，周国兴

1.南京航空航天大学 自动化学院, 江苏 南京 211106

2.南京航空航天大学 无人机研究院, 江苏 南京 211106

腿足式机器人能够在非结构式环境中具有较好的灵活性与适应性[1]。在足式机器人的领域中，双足机器人的稳定性欠佳，六足及以上又缺乏四足机器人的灵活性，因此，四足机器人已然成为新兴的研究热点[2]。四足机器人是MIMO的非线性动力学系统，迄今为止，四足机器人常用的控制方式有中枢神经控制、虚拟模型控制和零力矩点控制法3种。

基于零力矩点（zero moment point，ZMP）[3−4]的控制方式能够实现稳定的步行，在抗干扰方面也有优势，但是由于其需要实时考察其质心位置，并将关节轨迹通过逆运动学求解出，所需计算量较为巨大，甚至有些步态无法满足ZMP的要求；生物控制方法[5−6]，相比于广泛存在的基于模型和基于行为的控制方法，不需要进行复杂的数学计算和分析，方法相对简单，但是要想用于实际的工程中，需要结合生物运动资料或者优化算法来确定控制的参数。而且在复杂地形中，机器人会受到来自环境的较大扰动，野外的地形往往不平整[7]，因此很大程度上中枢模式发生器（central pattern generator，CPG）算法将不再适用。

虚拟模型控制（virtual model control，VMC）[8−9]方法综合考虑机器人躯体位置、速度及姿态的控制，通过参数可调，对位置与姿态进行综合跟踪，无需对逆运动学进行求解，控制效率高。麻省理工大学研制的Cheetah3[10]与Mini Cheetah采用虚拟模型控制与模型预测控制相结合的方式估计出足端触地的虚拟力[11]，并完成了跳跃[12]、后空翻等动作。张国腾等[13]在四足机器人上融合了虚拟模型控制，并得到了较好的控制效果。但是现有的虚拟模型控制并没有实现参数的跟随变化，因此引入模糊自适应参数，根据反馈误差对其控制参数进行自适应。

基于此，本文对四足机器人的运动控制开展研究，将自适应模糊控制算法和VMC算法同时运用到足端轨迹跟踪控制上，以实现四足机器人的控制参数在线优化，增强控制系统的稳定性和鲁棒性，同时，进行仿真实验，验证该控制方法的合理性。

1 四足机器人模型建立

本文所采用的四足机器人模型为全肘式，如图1所示。机器人有4条腿，图上方定义为机器人的前方，每条腿由3个关节组成，从上至下依次为：髋关节、大腿关节和小腿关节。

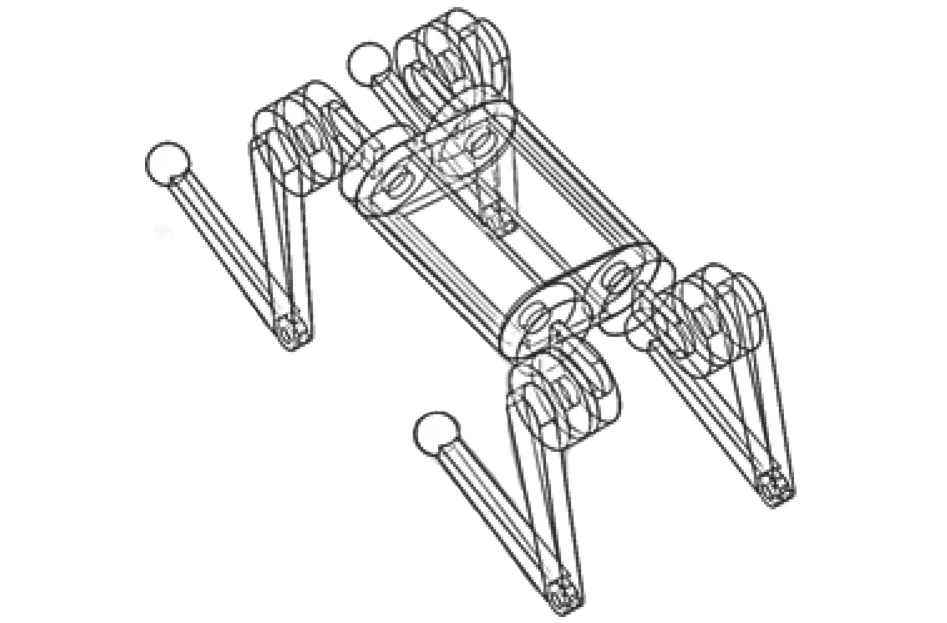
图1 四足机器人模型

采用D-H法建立四足机器人的运动学模型。由于四足机器人的四足对称，4条腿的坐标系建系都类似，因此只需给出四足机器人单腿简化的三维模型，保留了髋关节、大腿和小腿关节的自由度。如图2所示， θ1、 θ2、 θ3分别为髋关节、大腿和小腿关节的旋转角度。 θ1沿水平向下为正， θ2沿垂直向右为正， θ3沿小腿延长线向内为正，单腿坐标系的原点建立在髋关节的旋转中心上，x、y、z轴分别沿图2的箭头方向为正。

图2 单腿的运动学建模

图2中，L1、L2、L3分别为髋关节、大腿关节，小腿关节的长度，其数值在下文中给出。定义左前腿、右前腿、左后腿、右后腿为LF、RF、LR、RR。

根据图2单腿模型，可以求得四足机器人的正运动学方程为

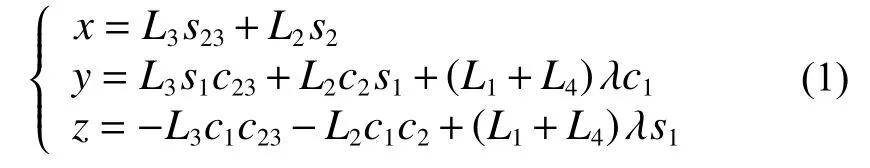
式中：x、y、Z为足端关于所对应的单腿髋关节坐标系的坐标，L1、L2、L3分别为髋关节、大腿关节、小腿关节的长 度，si= s in(→ı)，ci= c os(→ı)，siv¯= s in(i+j)，cij= c os(i+j)，λ为偏置参数，右前右后腿为1，左前左后腿为−1。

根据式（1）所述的四足机器人运动学方程，对x、y、z分 别求 θ1、 θ2、 θ3偏导，可得相应的雅克比矩阵：

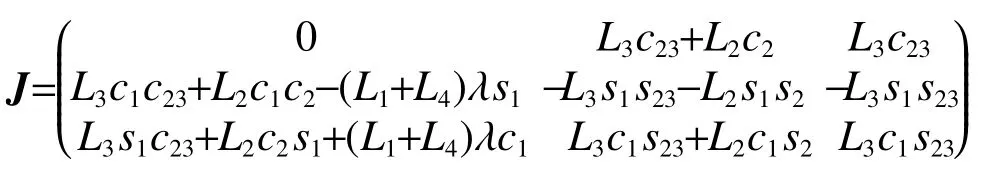
在腿部空间内，J为满秩，因此机器人在足端的3个方向上的输出力均是可控的。

2 VMC 虚拟力模型

2.1 VMC 控制原理

VMC所使用的控制方式，是通过假想的元件来连接内外部作用点，产生虚拟的作用力来驱使机器人的足端追踪期望轨迹。通过使用正向运动学求导得到机器人足端的雅克比矩阵，将足端的虚拟作用力映射到其关节力矩。其中，足端所给予的虚拟构件一般由弹簧与阻尼器组成，这样既保证其具有一定的伸展量，也保证能够更加稳定。

虚拟力的计算由式（2）给出：

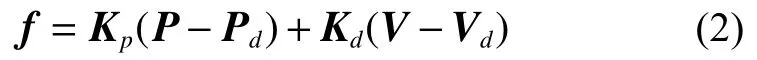
式中：f∈R3为所需的虚拟力，Kp、Kd∈R3×3分别为弹性系数矩阵与阻尼系数矩阵，P、V∈R3分别为足端的实际位置和速度，Pd、Vd∈R3分别为足端的期望位置和速度。当Kp=0时，可以控制机器人追踪期望的速度，而当同时启用Kp、Kd时，可以控制机器人追踪期望的轨迹。

关节力矩与虚拟力之间的关系可以用式（3）来呈现：

式中： τ ∈R3为各关节的力矩，F∈R3为式（3）得出的各关节的虚拟力。

2.2 摆动相控制

摆动的腿使用贝塞尔曲线[14]对足端的位置进行跟踪。贝塞尔曲线由线段与节点组成，节点是可拖动的支点。贝塞尔曲线通过起始点和终止点，并与起始点和终止点的折线相切，在对四足机器人路径规划过程中至少需要三阶贝塞尔曲线才能生成曲率连续的路径。贝塞尔曲线被广泛用于四足机器人的足端轨迹规划，其优点在于控制简单、描述能力强、易于生成平滑的曲线等。本文 采 取 的 轨 迹 为 三 次 贝 塞 尔 曲 线 ，P0、P1、P2、P3共4个点在平面或在三维空间中定义了三次方贝兹曲线，由于所使用的轨迹是对称的，所以在运用时有部分参数重叠。曲线的参数形式为

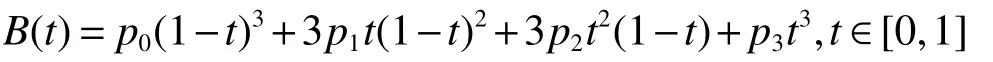
2.3 支撑相控制

在四足机器人运动的过程中，与地面接触的腿被称为支撑腿，支撑腿的关节力矩的计算公式为

3 基于自适应模糊的 VMC 控制器

3.1 控制器结构

在四足机器人运动过程中时，极易受到路面情况以及本身模型参数摄动影响。在跟踪的过程中，若VMC参数Kp、Kd固定，则控制器鲁棒性与抗扰性有限，容易造成力传递不平衡，从而使得控制效果（例如位置跟踪精度、响应速度等）下降。

针对上述问题，本文在虚拟模型控制的基础上，增加模糊控制的理论，设计一种自适应模糊虚拟模型控制器。该控制器能够根据实际位置与期望位置的误差及误差的变化率在线调节虚拟模型控制中的弹簧系数与阻尼系数，从而改善腿部跟踪期望轨迹的能力。自适应模糊控制器包括：模糊化、模糊推理和清晰化，对应的内容为输入隶属度函数、制定控制规则和逻辑判断。图3为自适应模糊VMC控制系统结构图。

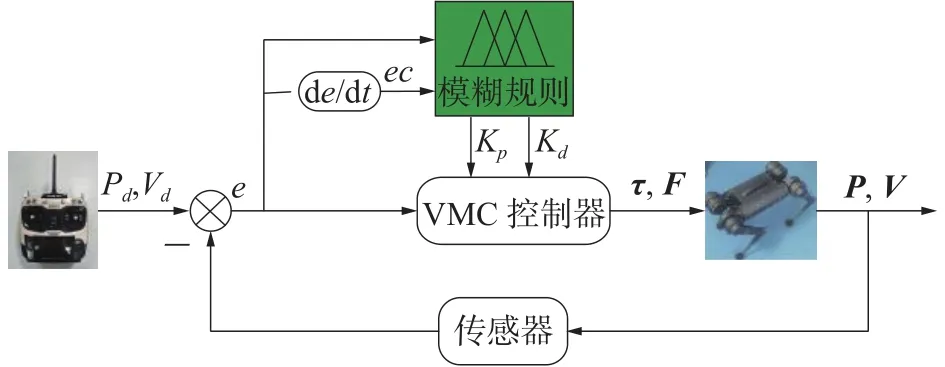
图3 自适应模糊 VMC 控制系统结构

此模糊控制器主要是需要完成变量的模糊化、模糊控制规则的制定以及清晰化3方面。

设Kp0、Kd0是虚拟模型控制中初始的弹簧系数与阻尼系数， ∆Kp、 ∆Kd是模糊控制器输出的2个参数，Kp、Kd是自适应模糊VMC控制的最后所得的参数。自适应模糊VMC控制器由式（5）给出：

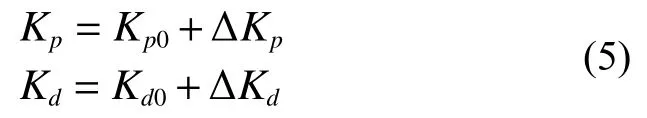
具体的逻辑为：取得实际的轨迹与期望的轨迹的差值e及其微分c，将其模糊化，再通过知识库与逻辑判断，得到模糊整定的 ∆Kp、 ∆Kd，最后通过式（5）计算得出Kp、Kd。

3.2 模糊化

建立Mamdani型二维模糊双输入双输出控制器。输入为控制变量偏差e以及其微分c，自适应虚拟模型控制器的输出量为控制器的调整值∆Kp、 ∆Kd。自适应虚拟模型控制的输入与输出的论域等级均为

输入量的模糊子集描述为

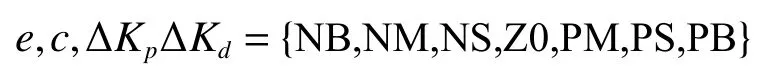
式中：NB、NM、NS、Z0、PM、PS、PB分别代表负大、负中、负小、零、正小、正中、正大。如图4、图5所示，选择隶属度函数为均匀分布的三角形函数。

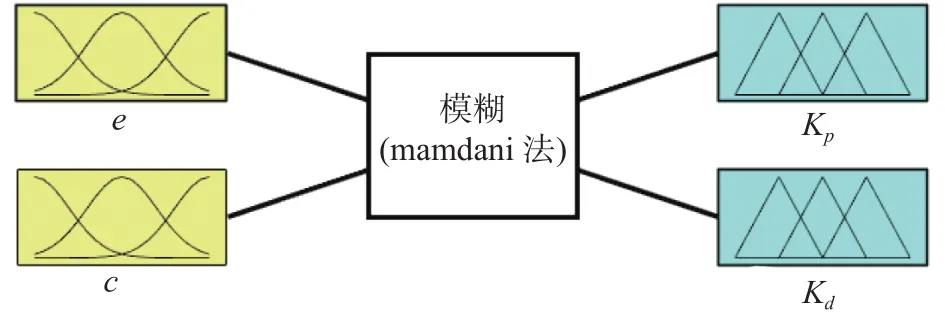
图4 模糊输入输出

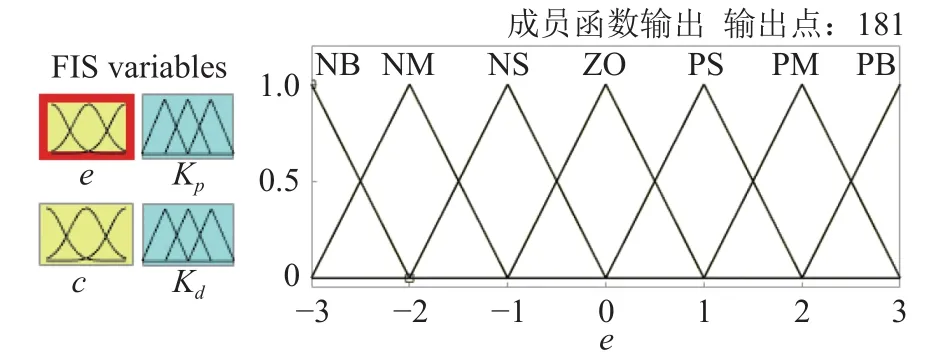
图5 隶属度函数

3.3 自适应模糊规则

自适应虚拟模型控制中的弹簧系数Kp与阻尼系数Kd，当弹簧系数过大时，系统的响应速度快，容易产生超调使系统不稳定；当弹簧系数小时，系统响应速度变慢，无法很好的跟踪轨迹，达到期望的效果。

综合各方面因素，建立2个参数的模糊规则如表1~2所示。

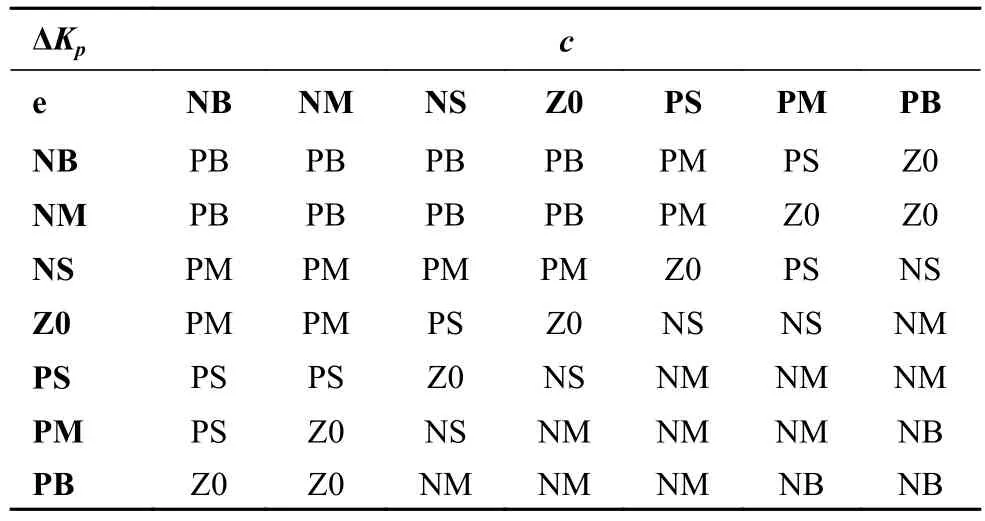
表1 Kp 规则

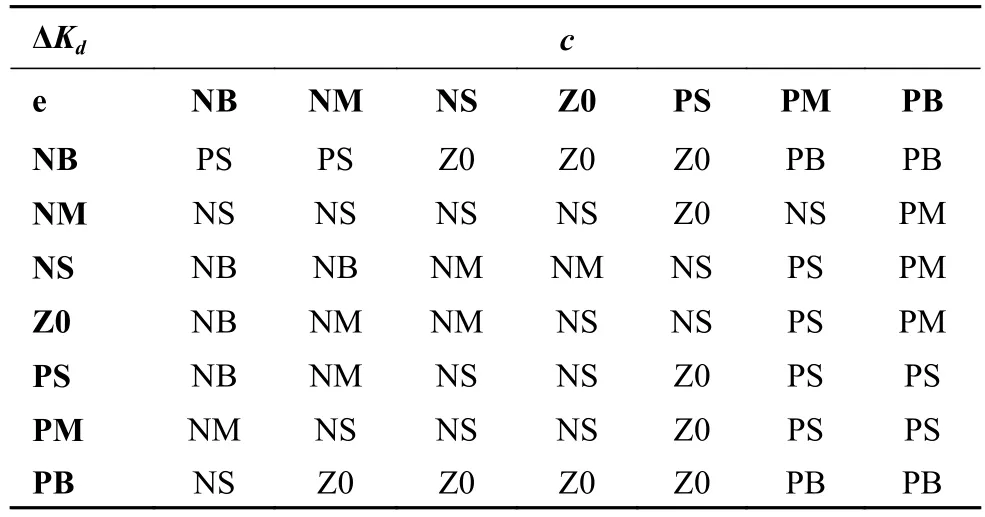
表2 Kd 规则

3.4 清晰化

采用Mamdani法进行了模糊推理，采用重心法进行解模糊的计算，计算公式如式（6）所示：

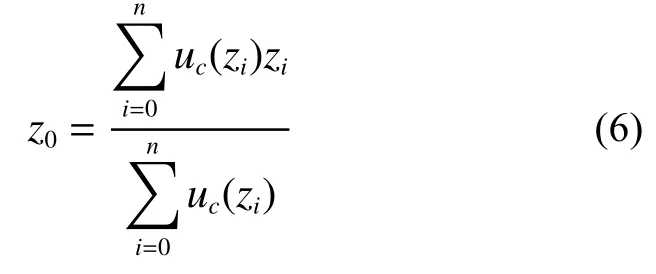
式中：z0为自适应模糊虚拟模型控制清晰化后输出的值，zi为模糊控制量论域中的值，utz(i)为zi的隶属度值。

模糊控制的 ∆Kp、 ∆Kd输出控制量曲面如图6~7所示。

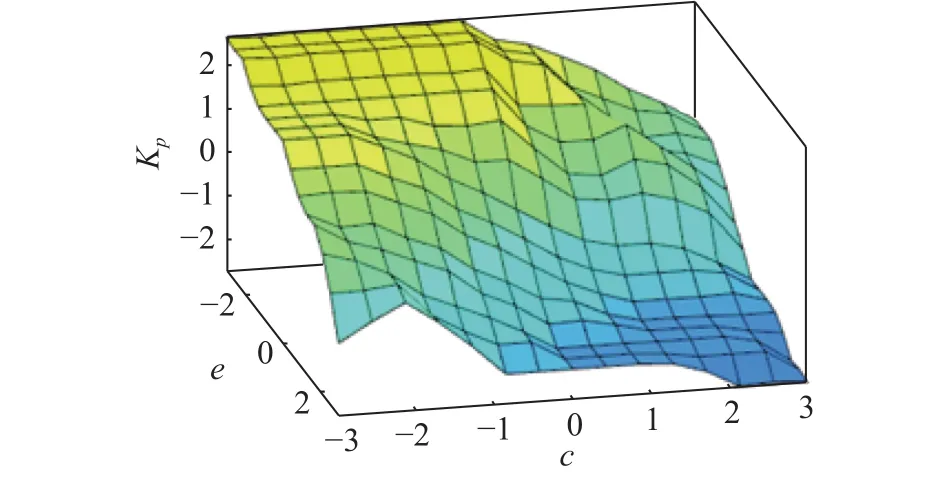
图6 Kp 曲面

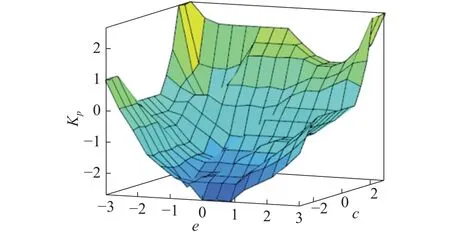
图7 Kd 曲面

4 仿真验证

为了验证自适应模糊VMC算法的准确性与稳定性，开展仿真实验，测试该算法在四足机器人tort步态下的性能。仿真所使用参数如表3所示。

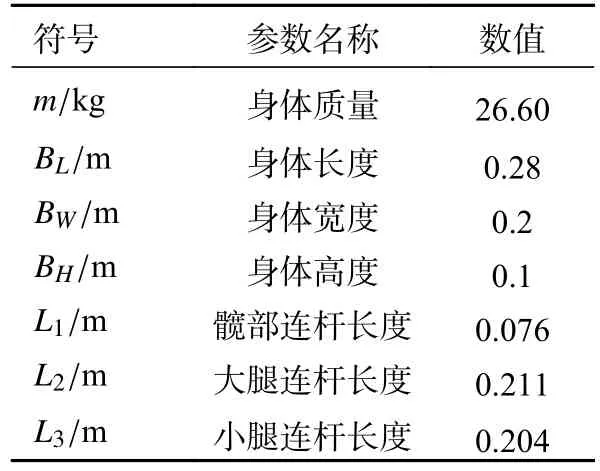
表3 仿真实验参数

建立对应的四足机器人模型，实验采用四足机器人典型的tort步态测试行走过程中控制器对于期望轨迹的跟踪能力。仿真过程如图8所示。

图8 仿真过程

对tort步态进行仿真实验，图9~图11为仿真实验过程中x、y、z实际与期望的轨迹曲线，在图9~图16中出现的t均代表仿真的单位时间步长。可以看出在x、y轴方向上曲线对于期望值有良好的跟踪能力，z轴虽然在跟踪过程中有短暂延时，但最终也能够稳定的跟踪上期望轨迹。

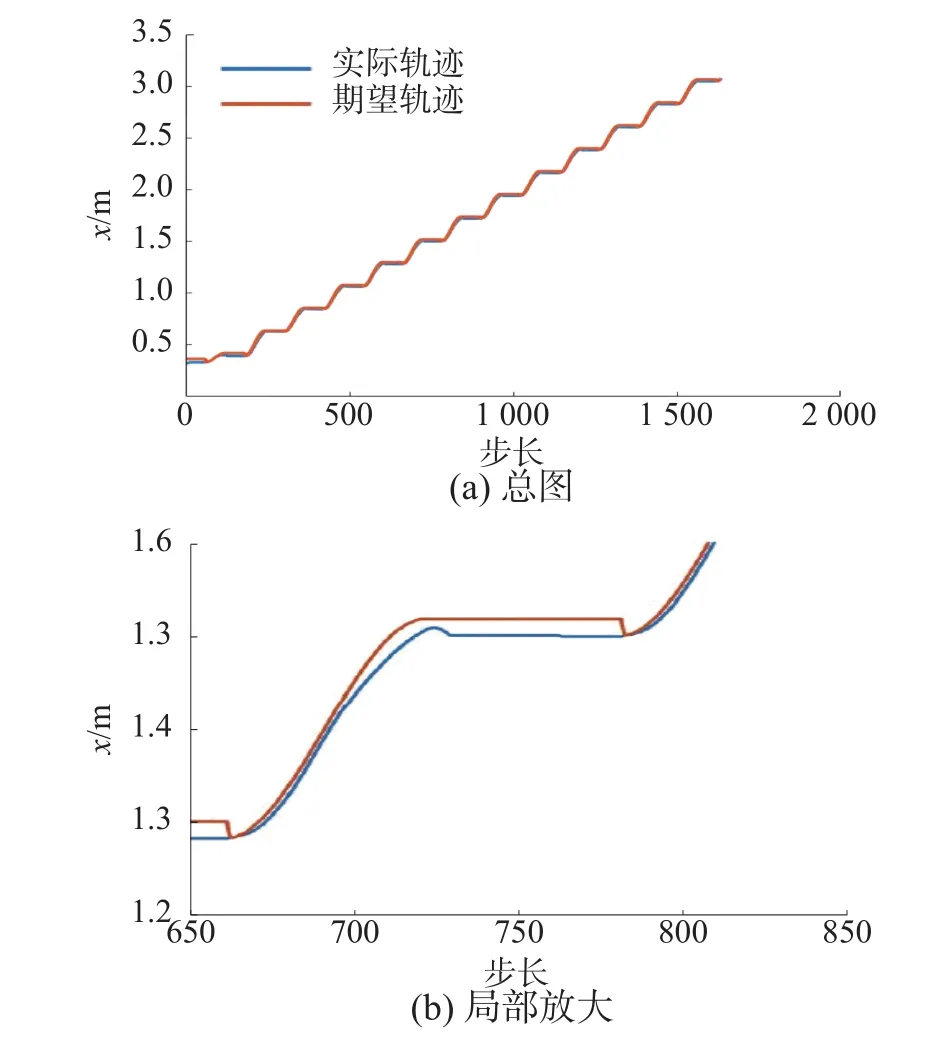
图9 x 轴跟踪曲线

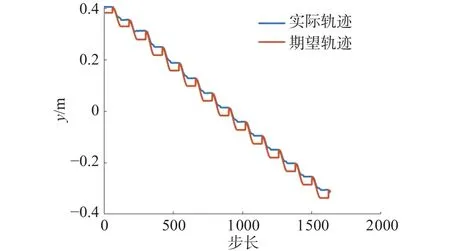
图10 y 轴跟踪曲线

图11 z轴跟踪曲线

图12所示，四足机器人运动过程中的质心实际轨迹与期望轨迹误差均保持在0.01m以内，运动平稳，控制效果良好。图13展示了运动过程中机体滚转角、俯仰角与偏航角的变化曲线图。在运动刚开始时，由于机器人有起身动作，姿态角有较大的波动，进入平稳行走状态后，姿态角保持稳定，波动较小。

图12 质心运动曲线

图13 姿态角变化曲线

图14和图15分别展示了在运动过程中Kp与Kd参数的变化曲线图。

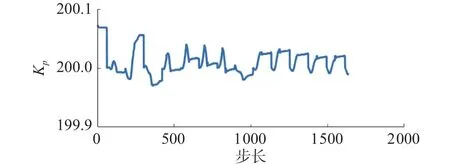
图14 K p变化曲线

图15 K d变化曲线

为进一步证明增加模糊算法对系统跟踪能力的提升，引入足端轨迹跟踪性能指标C。

式中：x、y、z为实际轨迹的三轴坐标，xd、yd、zd为期望轨迹的三轴坐标。

在每一个轨迹点进行C值的计算，最后得到关于C指标的曲线，与不采用模糊算法进行对比，如图16所示。

图16 C 曲线对比

C1为使用模糊算法优化过后的曲线，C2为未使用模糊算法优化的曲线。由图16分析可知，在任意时刻优化后C值均低于优化前。

5 结论

1）本文建立了四足机器人运动学与动力学模型，通过D-H法对机器人的四条单腿12个关节进行运动学建模，使用贝塞尔曲线作为摆动相轨迹，解决机器人的基本运动问题。

2）本文在四足机器人的动力学控制中采用虚拟模型控制，使机器人关节之间更加柔顺。针对传统的虚拟模型参数固定，不能根据运动过程调节的问题，在此基础上，引入模糊控制的算法，优化虚拟模型控制中的控制参数，以达到更好的跟踪效果。

3）通过仿真验证，从跟踪三轴期望轨迹，质心运动轨迹，足端跟踪性能指标等方面，证明了模糊算法的有效性，使四足机器人具有更好的跟踪期望轨迹的能力。

4）本文仅研究了单腿控制，在未来工作中，将把重点放在四腿联动控制上。