小尺度平面网衣流场特性数值研究
2022-03-25李鹏韩鑫悦秦洪德邓忠超
李鹏,韩鑫悦,秦洪德,邓忠超
1.哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2.哈尔滨工程大学 烟台研究 (生)院, 山东 烟台 264006
水产养殖为人类的日常生活提供食物和生物能源,据2018年联合国粮食及农业组织报告,2030年,海产品需求可能达到约1.8亿吨[1]。网箱养殖具有清污能力强、养殖产品质量高、对环境污染小等特点,网衣能限制海洋生物活动范围,保证网箱内外的水质交换,抗风浪破坏。而金属网衣具有耐腐蚀、抗风浪能力强、不易附着物等优点,应用逐渐广泛。研究金属网衣的阻力特性及其周围的流场特性关系着鱼群养殖的质量和网箱安全性。
在过去的几十年里,关于网衣的阻力特性及其周围的流场特性一直是热门课题,不同的学者进行了大量的研究。Løland[2]采用线性自由尾迹方程结合漩涡粘公式模拟了平面网周围的流场,研究了近场和远场尾流的运动特性,并与模型试验结果进行了比较。Tsukrov等[3]利用经验公式计算求得的网衣所受力的大小,利用等效网单元模型对网衣在波浪水流联合作用下的运动相应进行模拟。詹杰民等[4]采用物理实验和理论分析的方法,研究了网衣的水动力性能与雷诺数、攻角及网衣特征参数之间的关系。桂福坤[5]基于有效绕流面积系数假设理论,得出了平面网衣系统流速衰减的计算方法。Patursson[6]利用多孔介质模型来模拟平面网衣,研究分析平面网衣后的水流流速衰减情况。赵云鹏等[7−8]建立三维数值模型来模拟水流中平面网衣周围的流场,分析了不同攻角、不同高度和不同距离的两片网衣以及不同数量的平面网衣周围的流场特性。毕春伟等[9]运用集中质量法和多孔介质法数值模拟了流场和网衣之间的相互作用,然后计算分析了单片柔性网衣与不同间距的双片柔性网衣周围的流场特性。Liu等[10]基于有限元分析方法建立了动力有限元数值模型,对有周期性外力作用在网衣上的动力响应问题分析研究,研究发现雷诺数的大小和振动频率的高低都会对网衣的水动力系数产生影响。Hao等[11−13]提出了一种基于Morison型荷载模型转换的多孔阻力系数计算方法。
本文采用数值模拟方法,基于计算流体力学方法,利用STAR-CCM+软件,对不同雷诺数下、不同攻角、不同密实度以及不同网眼形状的平面网衣的阻力性能和网衣周围流场特性进行了研究分析。本文对明确平面网衣的流场特性具有一定的指导价值。
1 数值模型
1.1 控制方程和湍流方程
本文使用CFD方法进行数值模拟时,基于不可压缩粘性流体的运动,通过有限体积法求解流场的控制方程,不可压缩流的运动可以由雷诺平均Navier-Stokes方程系统描述,连续方程和动量方程可以表示为
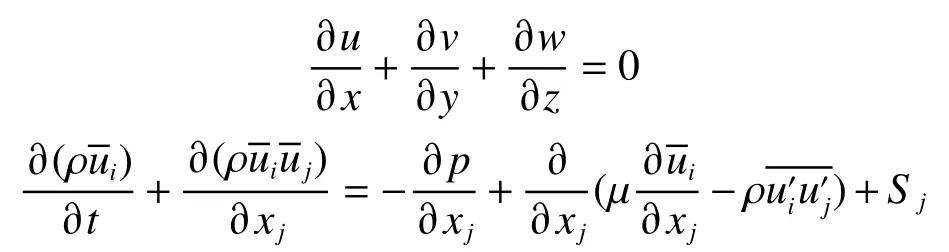
式中:u、v、w为速度U在3个方向上的分量,t为时间,p为流体受到的压力,μ为流体的动力粘性系数,ui为x、y、z方向的速度分量(i=1,2,3),u'为脉动速度。
在湍流运动包含着脉动应力项,该项使方程不封闭,因而必须对该项进行假设,即湍流模型。因为网衣对水的流动有着一定的阻拦作用,故网衣前后会存在不可忽略的压力梯度,Realizablek-ε模型能够对上述现象进行很好地模拟分析[14],所以本文选择 Realizablek-ε模型进行对湍流流动的模拟分析。
k方程:

ε方程:

式中:

k方程、ε方程中:Gk为由平均速度梯度产生的湍流动能,Gb为由浮力产生的湍流动能,YM为可压缩湍流中脉动扩散分布的整体耗散率,C2、C1ε和C3ε为常量,S为应变模量,σk和σε为k方程和ε方程的湍流Prandtl数,Sk和Sε为用户自定义的源项。Gb=0,YM=0,Sk=0,Sε=0。对于 Realizablek-ε模型,C1ε=1.44,C2=1.9,σk=1.0,σε=1.2。
1.2 相关参数
与本文中流体运动相关的无量纲系数为
雷诺数:
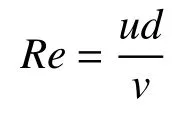
阻力系数:
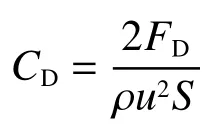
式中:u为流体的速度,d为网线的直径,S为投影面积,v为流体运动粘性系数,FD为物体阻力。
攻角 (angle of attack, AOA)α定义为流体正方向与网衣方向的夹角,如图1所示。

图1 攻角的定义
网眼密实度Sn定义为网线所覆盖的面积与平面网的总面积之比(Løland[2])。
对于方形网衣,参考文献[15]文章,其网眼密实度为

对于菱形网衣,参考文献[3]。如图2所示,在a×b矩形网衣有X×Y个菱形网格的情况下,对菱形网衣密实度定义为
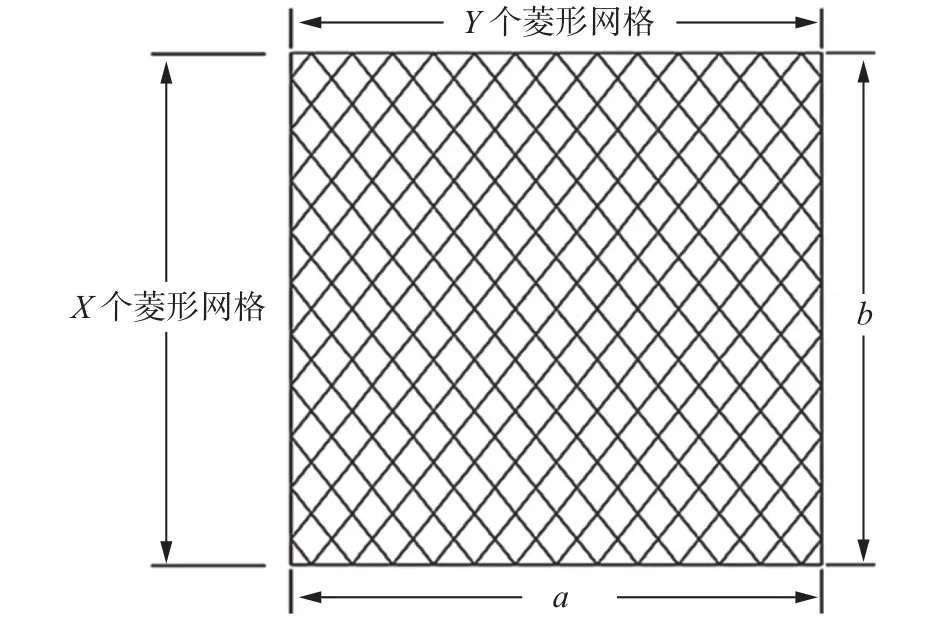
图2 菱形网眼网衣
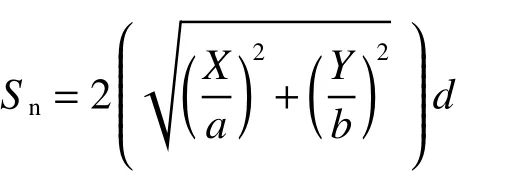
式中:a为菱形网衣长度,b为菱形网衣宽度,X为长度方向为菱形网格个数,Y为宽度方向上菱形网格个数,d为网衣网线直径。
目前没有对六边形网衣的密实度有确定的计算公式,故六边形网衣密实度Sn参考文献[2],为网线所覆盖的面积与平面网的总面积之比。
2 网格无关性验证
数值模拟使用的网衣为无结金属网,网线可简化为刚体,Tsukrov等[3]运用物理试验法研究分析纯流作用下不同材料网衣的阻力系数,本文选取其中的金属网进行数值模拟,考虑到后续计算的简便性,本文选取3×3小尺度网衣进行研究分析,直径dw为 0.001 35 m,网眼长度lw为 0.018 m,如图3所示。

图3 无结金属网衣
定义宽度方向为y轴方向,长度方向为x轴方向,为水流前进方向,垂直方向为z轴方向。设3×3网衣的总长度为l,流体进口距网衣中心4l,流体出口距网衣中心8l,左右上下各距网衣中心2l。流体域左侧为速度进口,右侧为压力出口,其余边界为对称平面,用以模拟无限流体域。网格采用切割体网格,对网衣和其壁面区域、网衣后尾流区域进行加密。图4为建立好的计算域和网格模型。采用4种不同尺寸的网格进行网格无关性分析,得到了不同数量网格网衣的阻力系数Cd。表1为网格无关性验证结果。
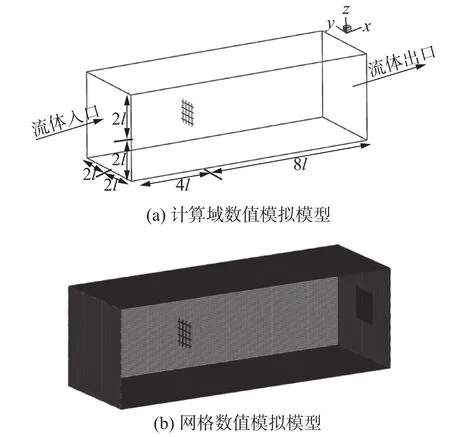
图4 计算域及网格

表1 网格无关性
当网格数量为127万和172万时,两者阻力系数相对误差为0.086%,说明已收敛,验证了网格无关性。考虑数值的准确性,网格数量采用127万。
3.1 雷诺数的影响
图5为α=90°时平面网衣在不同流速下的阻力系数,可以看出,随着雷诺数的增大,阻力系数逐渐减小。当速度从 0.1 m/s增至 0.5 m/s时,阻力系数平均降低了9.6%;当速度从1 m/s增至3 m/s时,阻力系数平均降低了3.7%,随着雷诺数的增加,平面网衣的阻力系数趋于平缓。
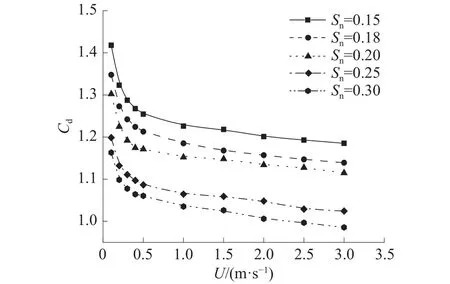
图5 不同流速 (雷诺数)下阻力系数
图6为α=90°时平面网衣在不同流速下的速度场分布。可以看出,流体流经网孔时流速增大,流过网衣后流速慢慢降低,但其尾流区域持续较长的时间。然而,对比不同雷诺数下速度分布的变化,可以发现雷诺数的变化并不影响尾流的宽度和区域。
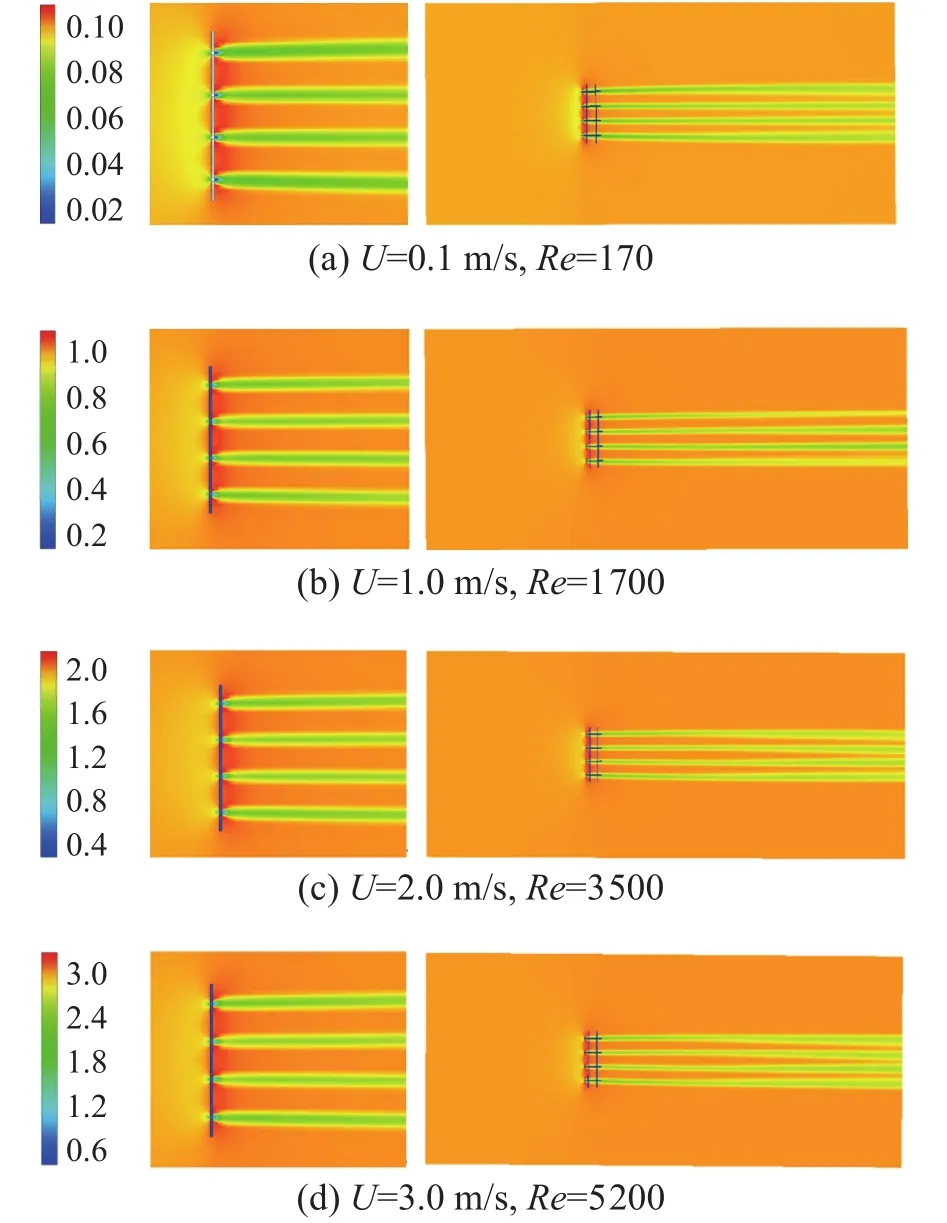
图6 不同雷诺数下网衣速度分布
为了更准确地描述速度的分布,绘制沿着网中心线的x方向流速衰减情况图,如图7所示。
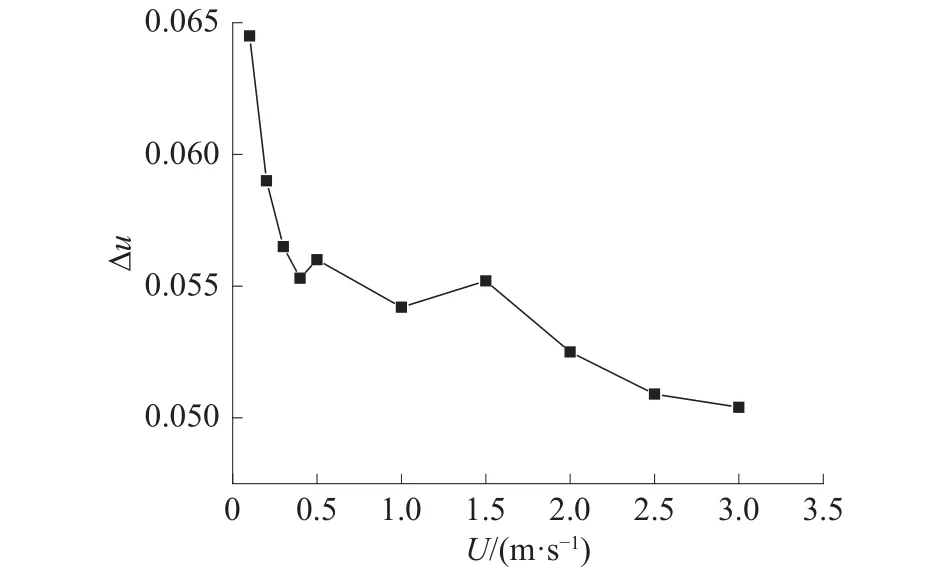
图7 不同雷诺数下速度衰减
其流速衰减幅度采用式(1)来计算:

式中:u0为速度入口处速度,u为网衣中心线上网孔处速度。
从图7可看出,不同雷诺数下速度衰减范围为5%~6.5%,可以近似认为雷诺数并不影响速度衰减。
3.2 AOA 的影响
图8为平面网衣在不同攻角下的阻力系数。可以看出,随攻角增大,阻力系数逐渐增大,当攻角在45°附近时,阻力系数增大相对明显。
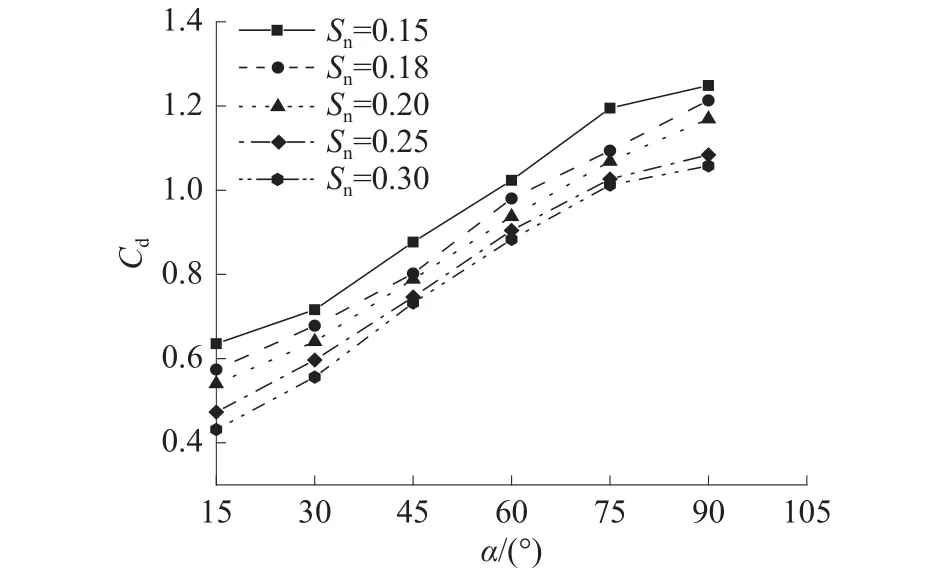
图8 不同攻角下阻力系数
图9为平面网衣在不同攻角下的速度分布。可以看出,随着攻角的增大,近场区域出现流速衰减范围越大,远场区域流速增大的范围也越大;网衣后尾流的宽度也逐渐增大,且流场越来越紊乱。
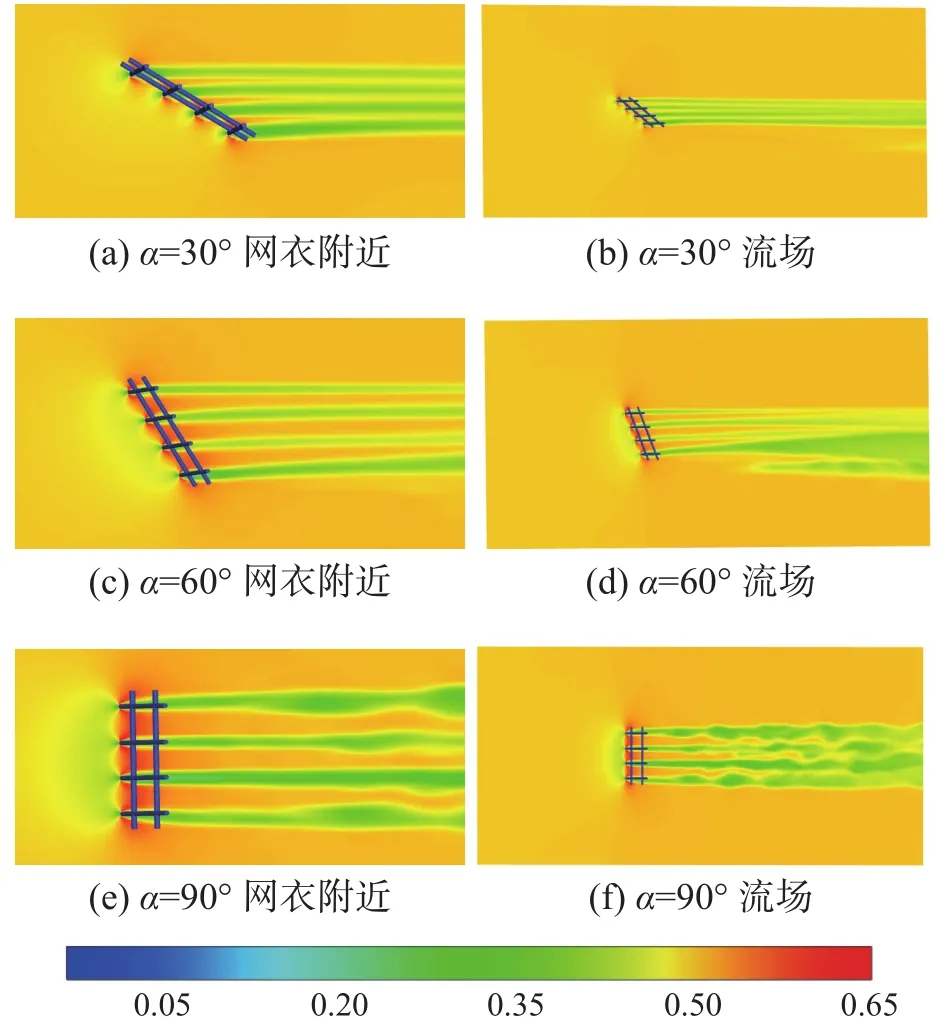
图9 不同攻角下网衣速度分布
为了更准确地描述速度的分布,绘制了沿着网中心线的x方向速度分布情况。图10为不同攻角下网衣中心轴线速度。
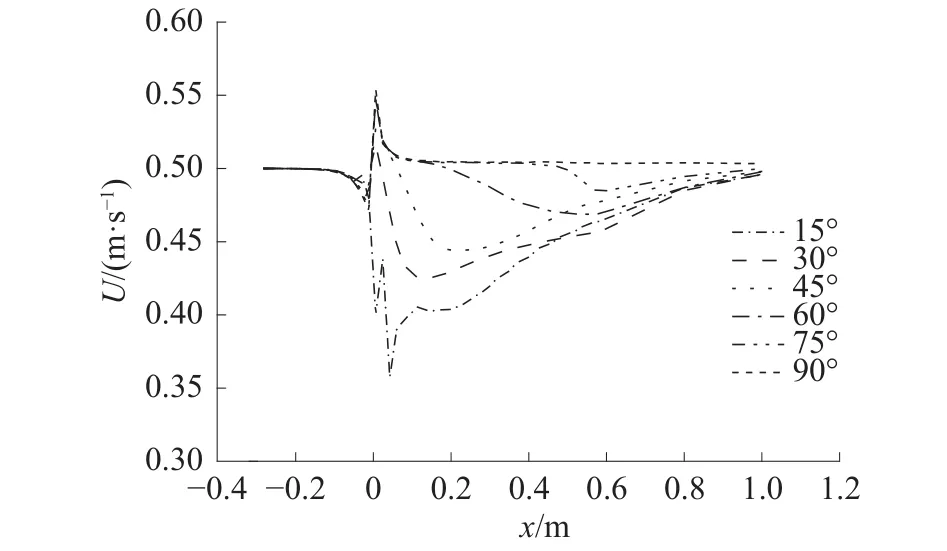
图10 不同攻角下网衣中心轴线速度
通过图10可以看出,当α≥30°时,水流流经网衣的过程中,速度先减小后增大,当攻角越大时,速度变化的幅值越小;水流流过网衣后,水流速度会恢复至0.5 m/s,攻角越小越快出现恢复的趋势。当α=15°时,水流流过网衣时,速度出现波动明显,呈现出先大幅减小,后小幅增大,而后大幅减小的趋势,最后趋于平缓。
3.3 Sn 的影响
图11为网衣在不同密实度下的阻力系数,随密实度的增大,阻力系数逐渐减小;当密实度由0.15增至0.2,阻力系数平均降低了10.1%,密实度由0.25增至0.3,阻力系数平均降低了4.2%,随着密实度的增加,阻力系数衰减的速率减缓。

图11 不同密实度下阻力系数
图12为网衣在不同密实度下的速度分布,可以看出,随着密实度的增大,近场和远场区域出现流速衰减的范围都越大,网衣后尾流的宽度逐渐增大,并且尾流越来越紊乱。流体流经网孔时,流速明显增大,而随着密实度的增大,其流速增大区域也越大。为了更准确地描述随密实度变化速度的分布,绘制沿着网中心线的x方向速度的分布情况。图13为不同攻角下网衣中心轴线速度。

图12 不同密实度下网衣速度分布
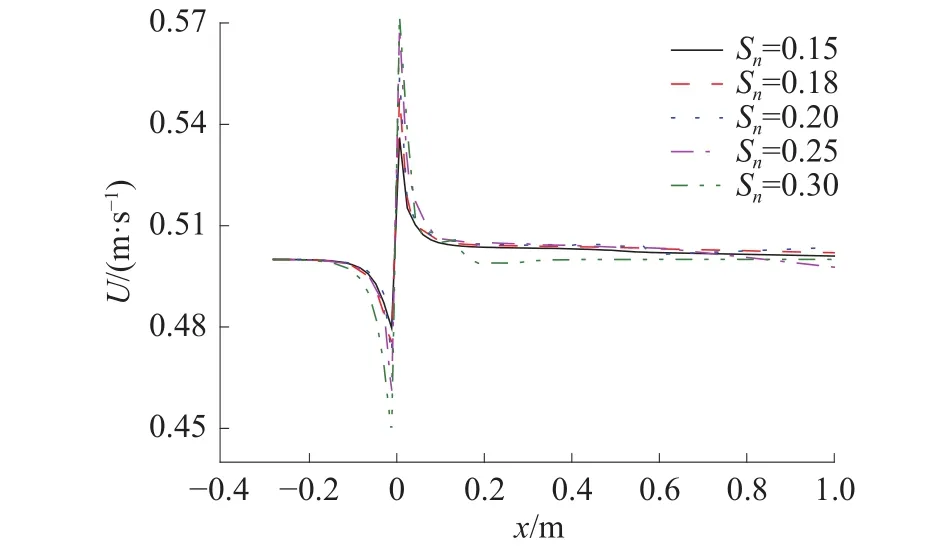
图13 不同攻角下网衣中心轴线速度
通过图13可以看出,在水流流经网衣的过程中,速度呈现先减小后增大的趋势。随着密实度的增大,速度变化的趋势也越大。即网眼密实度越大,网衣网线对轴线上的速度影响越明显。
为了更准确地描述速度的分布,绘制沿着网中心线的x方向流速衰减情况图,速度衰减幅度定义采用式(1)。
图14为不同密实度下速度衰减变化,可以看出,当密实度Sn<0.2时,速度衰减Δu小于6%,当密实度Sn=0.3时,其速度衰减Δu超过了10%,即密实度对速度衰减的影响较大。随着密实度的增大,速度衰减逐渐增大,速度衰减增大的速率基本不变。
3.4 网眼形状的影响
图15为平面网衣在不同密实度下的阻力变化,可以看出,当水流速度相同时,菱形网眼网衣所受的阻力最大,方形网网眼衣所受阻力最小。当水流速度较小时,网眼形状对网衣所受阻力的大小影响较小;随着水流速度的增大,不同网眼形状网衣所受的阻力相差越大。
图16为平面网衣在不同密实度下的速度分布情况,可以看出,水流流经网衣的过程中,近场区域流速都发生了衰减,网眼类型近场区域流速衰减程度影响不大。网眼类型对远场区域流速衰减现象影响较大,六边形网眼网衣后方流速衰减的幅值比较小,且流速越快恢复至0.5 m/s;菱形网眼网衣后方流速衰减幅值较大,且出现流速衰减的区域较大。
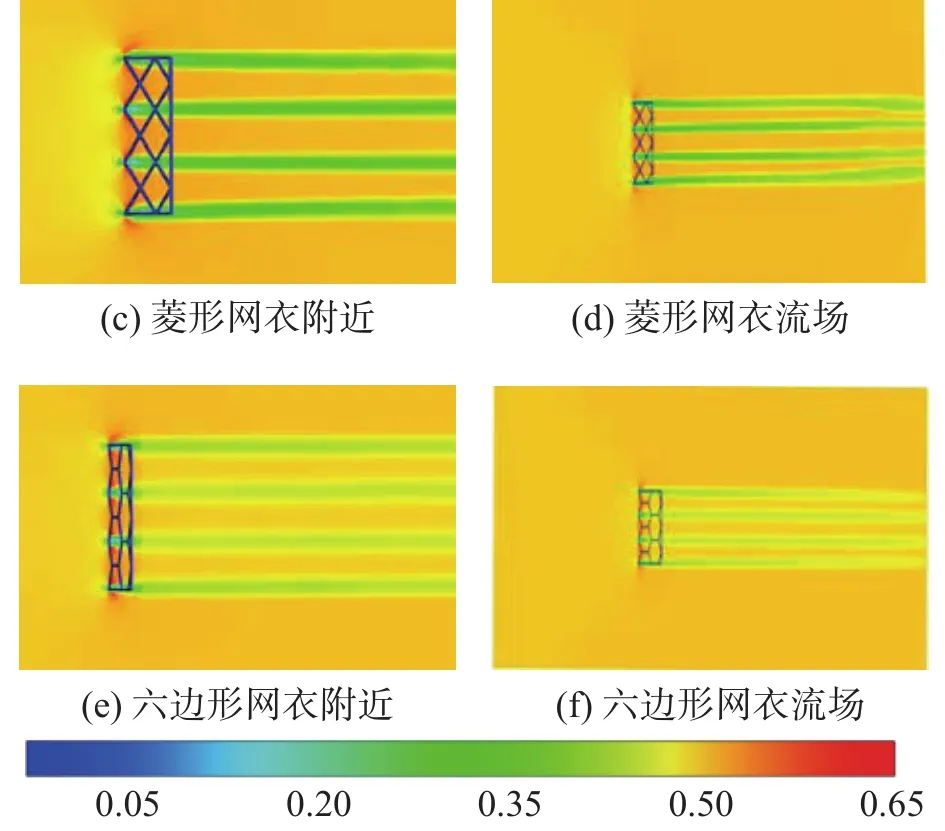
图16 不同网眼形状网衣速度分布
为了更准确地描述流场的状态,绘制了沿着网中心线的x方向速度分布情况,如图17所示。通过图17可以看出,在水流流经网衣的过程中,速度都呈现先减小后增大的趋势,且速度最后都会恢复至0.5 m/s。在水流流经网衣的最初阶段,水流速度会出现衰减,其中六边形网眼网衣较慢出现减小的趋势,且减小幅度为0.83%,方形网眼网衣流速衰减幅度为5.2%,即网眼形状对流速衰减影响较大;水流流经网衣时,水流速度会出现骤增,其中方形网眼网衣流速增大幅度为9.7%,六边形网眼网衣流速增幅为1.6%,网眼形状对网孔后流速增加的影响不可忽略;水流流经网衣的最后阶段,六边形网眼网衣的水流速度较快恢复到0.5 m/s。对水流流经网衣中心线速度进行对比分析可以发现,六边形网眼形状的网衣中心线速度变化最小。
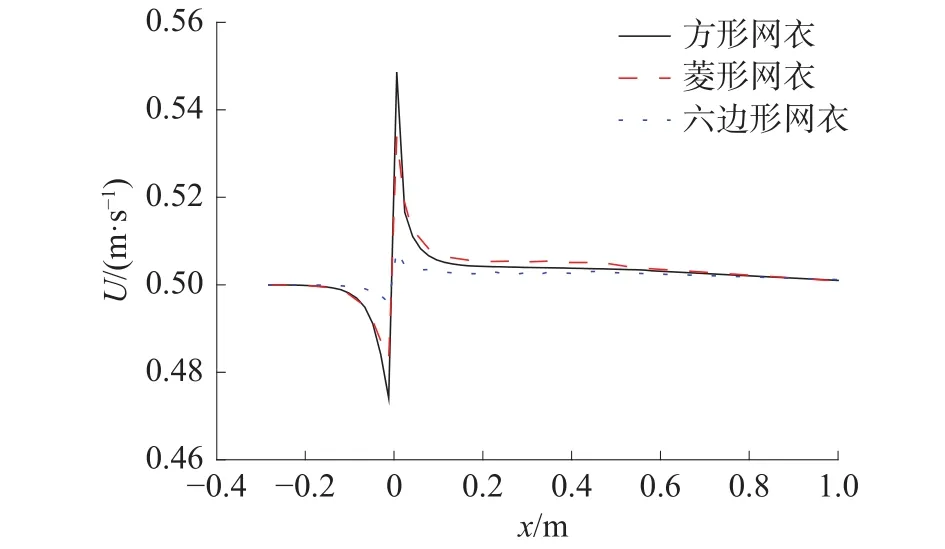
图17 不同网眼形状网衣中心轴线速度
4 结论
本文基于CFD数值方法,研究均匀流作用下小尺度无结网衣在不同雷诺数、攻角、密实度和网眼形状下的阻力性能和速度场分布。结论如下:
1)随着雷诺数的增大,网衣阻力系数逐渐减小,且减小速率逐渐降低,雷诺数对速度分布中网衣后尾流区域和流经网衣的速度衰减影响较小。
2)随着AOA的增大,阻力系数逐渐增大,网衣后尾流的区域越大且越紊乱;攻角较小时,流经网衣的水流速度的波动相对较明显。
3)随着密实度的增大,阻力系数逐渐减小阻力系数衰减的速率减缓,网衣后尾流的宽度越大,尾流越紊乱,网线对网衣轴线上的速度影响越明显。
4)当水流速度相同时,菱形网衣所受的阻力最大,方形网衣所受阻力最小;网眼类型对速度分布中网衣后尾流范围影响不大,六边形网眼形状的网衣中心线速度变化最小。
