船舶航向模型参考自适应和最优控制研究
2022-03-25包政凯朱齐丹杨司浩刘永超
包政凯,朱齐丹,杨司浩,刘永超
哈尔滨工程大学 智能科学与工程学院, 黑龙江 哈尔滨 150001
随着经济全球化的大力推进,世界海洋航运得到了蓬勃的发展,海洋资源的开发和保护逐渐引起了研究者的广泛关注[1]。与此同时,我国也提出海洋强国战略,对船舶和海上装备的节能、绿色、智能化提出了更高的要求。船舶作为海上主要的载运工具,在开发和利用海洋资源的过程中起着非常重要的作用[2]。船舶航向自适应控制是船舶运动控制领域中非常基础的研究问题。
船舶自动舵最早起源于1890 年Hopkins电动陀螺仪的研究成果[3]。1911年 Elmer Sperry首次提出了使用反馈控制和自动增益调整船舶转向机构,随后Nicholas Minorsky设计了一个位置反馈控制器,采用3项控制律,被称之为比例积分微分(proportion integration differentiation, PID) 控 制[4]。PID控制器具有设计简单、鲁棒性强的优点,但航向控制精度与操舵能耗难以满足当前自动舵的需求,且算法对船舶航速、装载与海况的适应能力较差,需要重复调参。为了解决以上问题,很多的船舶航向自适应控制算法被相继提出,主要分为自校正自适应和模型参考自适应两大类,Nguyen等[5]通过自适应舵对比研究发现模型参考自适应控制更适用于船舶转向控制过程,而自校正自适应控制更适用于航向保持过程。Velagic等[6]设计了模糊自适应航迹保持控制算法,在海流和海浪干扰环境下取得了较好的控制效果。刘志全等[7]设计了状态扩张观测器对船舶转向过程中的漂角进行估计和补偿,提高了航向跟踪精度。文献[8]针对航向非线性系统,提出了自适应鲁棒控制方法。对于含有参数不确定的船舶航向非线性模型,文献[9]结合自适应技术和逆推算法提出了航向自适应跟踪控制器。文献[10]针对带有海浪扰动的船舶模型,通过构造扰动观测器观测海浪扰动,基于反步法设计了航向保持控制策略。文献[11]集合模糊逻辑系统和最优控制算法,提出了船舶航向自适应模糊最优控制跟踪策略。以上研究成果未详细考虑实际应用过程中的角速度误差、打舵次数等性能指标需求,在应用中可能有一定局限性。
本文设计了微分跟踪模型参考自适应控制算法和自校正线性二次型高斯最优控制器(linear quadratic gaussian optimal controller,LQG)算法,实现船舶恒定角速度转向、保证航向保持精度的同时,降低打舵次数,使用海兰信自动舵半实物仿真平台,完成自适应舵ISO11674标准测试,所统计性能指标均满足标准要求,验证了所设计算法的有效性。
1 船舶航向微分跟踪模型
远洋航行的船舶多工作在航向保持模式下,该工况下船舶自动舵通过给定小舵角抵抗海洋环境干扰,使实际航向保持在期望航向误差带内,准确的航向模型是实现高精度航向控制的前提。
1.1 船舶航向模型
船舶操纵运动模型可以采用一阶线性Nomoto模型[12]:

式中:r为船体艏摇角速度;r˙为艏摇角加速度;ψ为船舶艏向角;δ为舵角;K、T为船舶回转能力和回转惯性参数,受到船舶载荷条件和航行速度的影响。船舶在快速转向过程中,航向模型具有非线性特性,考虑到ISO11674测试标准中,自适应舵测试预设转向角速度最高为40 (°)/min,是慢速转向过程,且自适应舵大部分时间工作在航向保持阶段,其非线性特性可以忽略,因此本文中使用线性模型。
1.2 微分跟踪器
微分跟踪器 (tracking differentiator,TD)可以将阶跃输入信号转化为二阶导数限幅下的连续最快跟踪信号,同时输出跟踪信号的一阶导数。当输入信号的二阶导数在TD限幅值以内时,TD可以快速跟踪输入信号,并估计出跟踪信号的一阶导数值。经典微分跟踪器具体形式为[13]

式中:u(k)为输入信号,m1(k)为跟踪信号输出,m2(k)为跟踪信号的微分输出,h为滤波因子,r为速度因子,T为跟踪步长,fst函数计算跟踪信号二阶导数,计算过程为

根据船舶恒定角速度转向的需求,对式(2)中的微分信号m2(k)添加饱和限幅,可得饱和微分跟踪器 (saturation tracking differentiator, STD)。

式中:sat为饱和限幅函数,vm为 微分信号m2(k)的限幅值。将STD应用到船舶航向控制中,如图1所示。

图1 船舶航向微分跟踪控制系统框图
图1中, ψs为 航向设定值, ψd和 ψ˙d分别为期望航向和期望角速度。选取系统状态为x1=ψ−ψd、x2=r−ψ˙d、x=(x1x2)T,考虑到航向保持和恒定角速度转向的需求,设 ψ¨d=0,则原系统状态空间方程式(1)可写为

2 船舶航向自适应控制器设计
船舶航行过程中,由于航速、装载的变化以及外界海况的影响,其航向模型存在不确定性。大部分船舶都装备了GPS,能够测量船舶速度信息,航速引起的参数变化可以采取经验公式的形式进行补偿。但是装载和海况等因素引起的船舶模型参数变化不容易补偿,因此需要在航向控制器设计过程中引入自适应机制克服船舶模型参数变化产生的不利影响。
船舶航向自适应控制可分为预设角速度转向控制和航向保持控制2部分。船舶航向保持过程中,检测到航向设定值发生改变后,控制器自动切换为预设角速度转向控制算法,直到航向和角速度进入误差带以内,再自动切换回航向保持控制。
为了实现船舶转向过程中的恒定角速度控制,将微分跟踪器引入了模型参考自适应控制,提出了微分跟踪模型参考自适应船舶转向控制器。
2.1 微分跟踪模型参考自适应控制器
对于式(3)状态空间模型,需要将跟踪误差x=(x1x2)T镇定到零,设计了微分跟踪模型参考自适应控制律为

将式(4)代入式(3)中,整理得:

取

则闭环系统的状态空间模型可以写成

选取参考模型

式中:

令e=xm−x, ∆A=Am−A, ∆B=Bm−B, 式(6)−式 (5)得:

选取李雅普诺夫函数:

式中:P为方程 −Q=PAm+的正定解,Q为正定矩阵, ΓA=diag{ γA1,γA2} ΓB=diag{ γB1,γB2},李雅普诺夫函数对时间求导可得:
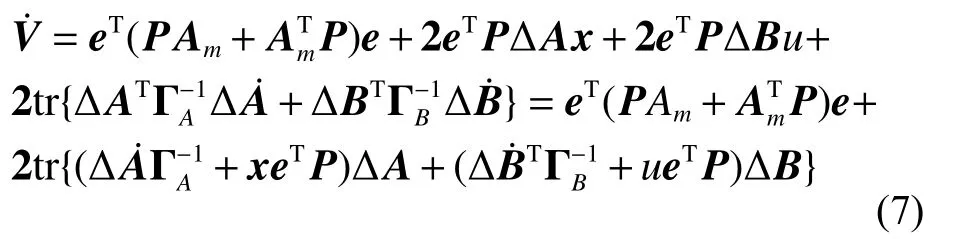
选取如下自适应律:

展开得
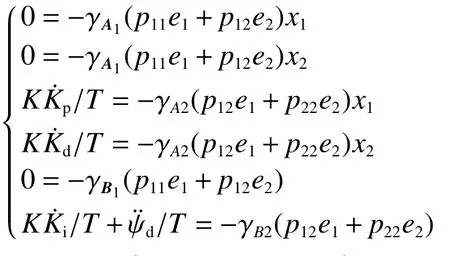
令 γA1= γB1=0, γp= γd= γA2T/K, γi=γB2T/K,=0,整理得自适应律:

以下证明控制律式(4)与自适应律式(9)的控制系统稳定性,将式(8)代入式(7)中有:


由于V有界,e、∆A、∆B均有界,又因为e、xm有界,x有界,u、Am分 别为有界输入和有界参考模型 参 数 , 故V¨ 有 界 , 从 而一 致 连 续 。 根 据Barbalat引 理 ,V˙|t→∞=−eTQe|t→∞=0,Q正 定 , 则e(t→∞)=0。
2.2 自适应 LQG 控制器
船舶航向保持控制状态下,船舶艏摇角速度几乎为零,且罗经角速度测量值中有较多噪声。线性二次型高斯最优控制器(linear quadratic gaussian,LQG)使用卡尔曼滤波器估计船舶艏摇角速度信号,结合最优控制律实现高精度航向控制。引入参数自适应机制可应对海洋环境干扰引起的参数不确定性。
2.2.1 参数自适应律
船舶航向模型(1)中的K、T参数采用满秩分解最小二乘法[14]进行估计。模型参数化形式为


满秩分解最小二乘法参数估计包括总迭代和主成分迭代两个组成部分,总迭代式为

主成分迭代式为
两部分关系为

式中:Vk1为满秩分解矩阵,可通过以下方式求取,设第k次测量数据 {hk,zk}对应的变换阵为Vk=[Vk1Vk2]

式中:hki为数据向量hk的 第i个分量,hs为死区阈值。
2.2.2 状态扩张卡尔曼滤波器
将式(1)整理为状态空间模型形式可得卡尔曼滤波器状态预测方程

式中:h为采样周期,wr和vr为干扰和测量噪声。令
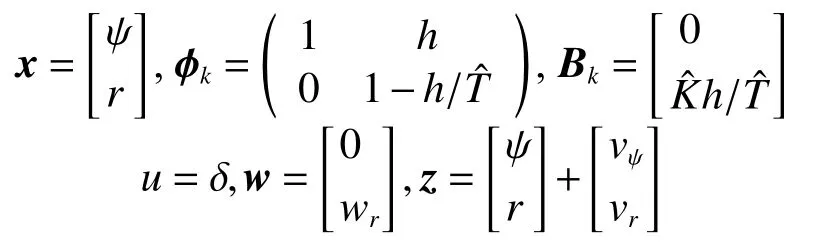
则状态预测方程可简写为

状态扩张卡尔曼滤波器的计算步骤如式(12),分别为状态预测、方差阵预测、计算增益矩阵、计算新息、状态更新、扩张状态跟新和方差阵更新。

式中:P为状态估计误差方差阵,Q为模型误差方差阵,R为测量噪声方差阵。
2.2.3 线性二次型最优控制律
最优控制律的目的是保持航向控制精度和节省能耗,选用二次型指标:

对应黎卡提方程为
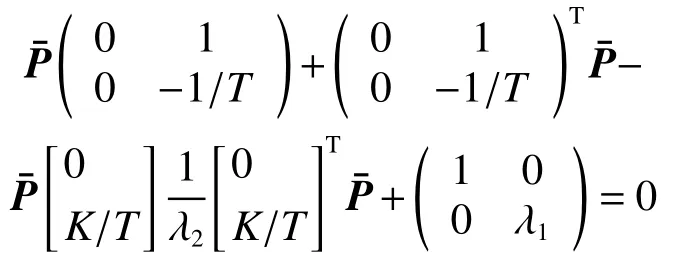
解得最优控制律为

3 半实物仿真平台测试实验
3.1 半实物仿真平台
本文采用的半实物仿真平台是北京海兰信数据科技股份有限公司提供舵机控制系统HLDSGCS 600,利用此系统完成控制算法有效性验证及性能测量。半实物仿真平台主要由船舶运动模拟器、算法模块、信号转换单元、操舵仪模块(主要包含操舵控制单元、舵角反馈单元、舵机模拟器等)4个部分组成。
船舶运动模拟器根据不同船型显示船舶的运动状态,模拟的船舶运动参数如表1。

表1 仿真船舶参数
图2是操舵仪模块,能够完成航向输入、船舶运动性能输出自动航向控制的用户界面,可以显示操舵模式、设定航向、当前航向、当前航向源、速度、转向率、操作响应等信息。同时,操作者还可以通过自动操作单元设置控制参数。

图2 操舵仪模块
图3为仿真平台的框架图,船舶运动模拟器产生标准NMEA语句;算法模块依据接收到的传感器信息、设定航向、船舶参数等信息,计算出舵令,发送舵令语句至信号转换单元;信号转换单元将舵令转换成CAN通信,发送至操舵仪模块;操舵控制单元执行舵令;舵角反馈单元采集舵机模拟器角度,发送舵角反馈值至船舶运动模拟器与算法模块。

图3 仿真平台框架图
3.2 实验测试结果与分析
实验测试主要分为基于线性二次型最优控制算法的航向保持测试、基于自适应算法的转向测试、转向性能对比测试3部分。航向保持测试主要考察打舵频率、打舵幅度、航向控制精度等方面;转向测试主要考察转向快速性、转向过程稳定性、转向超调及欠调等方面。为方便对比分析转向算法的优越性且线性二次型最优控制也具有转向的功能,将自适应LQG控制器与线性二次型最优控制都应用于航向转向测试中,验证自适应LQG控制器转向性能指标优越性。
3.2.1 航向保持测试
A船航向保持测试,航速20 kn,5级海况;B船航向保持测试,航速20 kn,5级海况;C船航向保持测试,航速10 kn,5级海况。仿真平台运行时间 540 s,A、B、C 船航向保持测试过程航向变化、角速度变化、舵角变化曲线如图4~6。

图4 航向保持测试航向变化曲线

图5 航向保持测试角速度变化曲线
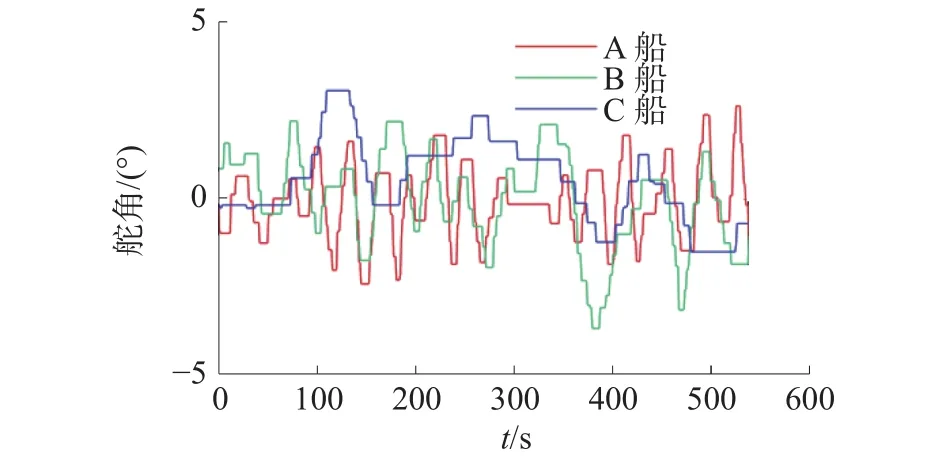
图6 航向保持测试舵角变化曲线
对上述实验进行性能统计可得表2:

表2 航向保持试验性能统计
表2中性能指标说明:1)打舵频率为每分钟的打舵次数,舵角指令每变化0.1°则记为打舵1次;2)打舵幅度为航向保持过程中最大的舵角幅度;3)航向控制精度为航向保持过程中绝对航向误差均值。实验结果表明本文设计的航向保持算法具有打舵次数少、控制精度高等优点,针对不同船型同样有优越的航向保持控制效果。
3.2.2 自适应转向测试
A船转向测试,航速20 kn,5级海况;B船转向测试,航速 20 kn,5级海况;C船转向测试,航速 10 kn,5 级海况。
A、B、C 船由 180°~210°的+30°转向测试过程航向变化、舵角变化曲线如图7~图9所示,仿真平台运行时间 380 s。

图7 +30°转向测试航向变化曲线

图8 +30°转向测试角速度变化曲线

图9 +30°转向测试舵角变化曲线
A、B、C 船由 210°~180°的−30°转向测试过程航向变化、舵角变化曲线如图10~图12所示,仿真平台运行时间 420 s。在 210°~180°转向中 A 船转向较快,在200 s数据采集停止。
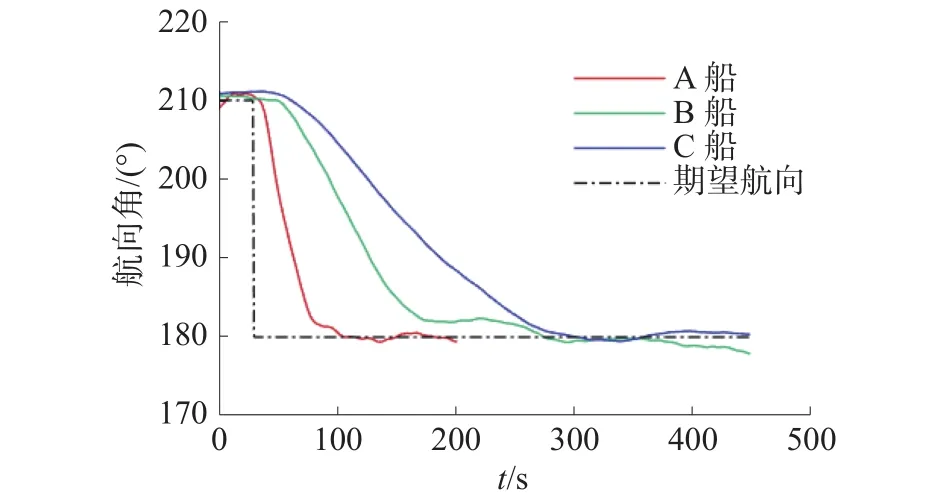
图10 −30°转向测试航向变化曲线

图11 −30°转向测试角速度变化曲线

图12 −30°转向测试舵角变化曲线
3.2.3 转向性能对比测试
A船转向测试,航速20 kn,5级海况,自适应LQG控制算法与线性二次型最优控制算法应用于航向转向测试中。由 180°~210°的+30°转向测试,转向测试过程航向变化、舵角变化曲线如图13~图15。对上述转向实验与转向对比实验进行性能统计可得表3。

表3 转向试验性能统计

图13 +30°转向对比测试航向变化曲线

图14 +30°转向对比测试角速度变化曲线

图15 +30°转向对比测试舵角变化曲线
转向实验性能指标说明:1)转向快速性:每次转向的调节时间;2)转向过程稳定性:为转向过程中是否会出现停滞回退等现象;3)转向超、欠调:每次转向实验时超欠调度数。
从性能指标统计结果可知采用自适应LQG控制算法的船舶的转向时间短、超调量小、转向稳定性高,针对不同船型、不同转向角度,在5级海风干扰下均能达到良好的控制精度,具有优越的自适应能力和鲁棒性。
4 结论
本文对比研究了微分跟踪模型参考自适应控制和自校正LQG自适应控制2种船舶航向控制算法。基于ISO11674自适应舵标准统计测试统计2种算法性能指标结果显示,所设计算法均达到自适应舵标准要求,且具有航向、转向角速度控制精度高和航向保持过程中打舵次数少的优点,算法具有较高实用价值。
针对自适应舵标准测试的需求,本文控制器设计仅考虑了船舶航向线性模型,未来可以考虑进一步应用到船舶航向非线性模型中。
