稀土金属钆在双辊薄带连铸过程中流动、传热和凝固行为的数学模拟
2022-03-25余建波任忠鸣
俞 晟 余建波 任忠鸣
(1.上海大学省部共建高品质特殊钢冶金与制备国家重点实验室,上海 200444;2.上海大学材料科学与工程学院,上海 200444)
钆是一种稀土金属,其4f轨道上存在几个未配对的电子,具有稀土元素中最高的磁矩,产生铁磁性[1-2]。室温下,钆发生二级反应铁磁-顺磁相变,具有较大的磁热效应,因此引起了广泛的关注和研究[3]。目前虽然对钆的性能和制备方法进行了大量的研究,但是如何快速生产单质钆仍然是一个值得探究的课题。
双辊薄带连铸技术是一种将连铸和轧制整合的前沿冶金技术,目前已应用于多种金属材料[4-6],为高效生产单质钆提供了一种思路。在双辊薄带连铸较高的铸轧速度下,实现钆液流场、温度场的合理分布以及凝固坯壳的稳定生长,将成为应用双辊薄带连铸生产单质钆的关键。
近年来,研究者对双辊薄带连铸过程中的流动和传热行为进行了一系列的数学模拟研究。潘丽萍等[7]通过建立二维双辊薄带连铸凝固区的数学模型来计算凝固终点的位置。董建宏等[8]通过三维数学模拟考察了布流器结构、开孔倾角等工艺参数对不锈钢熔池流场和温度场的影响。Xu等[9]利用三维焓-多孔介质混合凝固模型描述了多端口槽形布流系统双辊薄带连铸机内钢液的流动、传热和凝固的基本规律。Xu等[10]也采用二维数学模型对比了钢和铝在双辊薄带连铸过程中流动、传热和凝固过程的差异。徐益龙等[11]使用微元模型研究了结晶辊温度分布对双辊薄带连铸凝固过程的影响。
显然,材料的物理性质不同,在双辊薄带连铸过程中的流动、传热和凝固行为必然存在较大的差异。据此,本文针对自行设计的辊长50 mm、辊径100 mm和辊距2 mm的双辊薄带连铸机,以稀土金属钆为研究对象,建立三维流动和传热数学模型,探索不同浇注温度下钆液在双辊薄带连铸过程中的流动特征、传热规律和凝固行为,为应用双辊薄带连铸技术生产单质钆提供理论指导。
1 数学模型
1.1 模型描述
稀土金属钆的双辊薄带连铸过程示意图如图1所示,工艺参数如表1所示。钆液从直通型水口流入熔池,在两侧不断旋转的结晶辊持续冷却下形成一层凝固坯壳,随后被轧制成一定厚度的薄带并被连续拉出结晶辊区域。考虑到结晶辊以及钆液的流动沿中心对称面有较好的对称性,因此沿中心对称面建立1/4模型,如图2所示,从而减少网格数和计算时间。

图1 双辊薄带连铸过程示意图Fig.1 Schematic diagram of continuous casting of twin-roll strip

图2 几何模型和边界条件示意图Fig.2 Schematic diagram of the geometric model and boundary conditions

表1 模拟工艺参数Table 1 Simulated process parameters
此外,考虑到液态钆与钢液的性质存在一定差异,因此在本文研究中,结晶辊的转速小于钢液浇注所采用的常规转速,定为0.1 m/s。
模型全部采用六面体网格进行划分,网格最大尺寸为0.5 mm。模型包含237 980个网格。
1.2 基本假设
实际浇注过程中,铸坯的冷却涉及流动、传热、凝固等一系列复杂的冶金过程。为了能用数学模型描述这一过程,需要对模型进行简化。基本假设如下:
(1)熔池内钆液假设为均质、不可压缩的牛顿流体;
(2)浇注过程为稳态,过热度和结晶辊转速都保持恒定;
(3)忽略水口钆液冲击对液面波动的影响;
(4)固态相变潜热远小于凝固潜热,因此忽略固态相变潜热的影响;
(5)忽略铸坯的收缩以及结晶辊的热变形。
1.3 控制方程
双辊薄带连铸过程中,钆液的流动和传热遵循连续性方程、动量方程和能量方程。同时,使用标准k-ε模型来描述钆液的湍流行为。具体控制方程如下。

式中:μ是动力学黏度,Pa·s;σk和σε分别是k和ε的湍流普朗特数;Gk是平均速度梯度产生的湍流动能;C1ε和C2ε是常数;Sk和Sε是用户自定义源项。
能量方程:
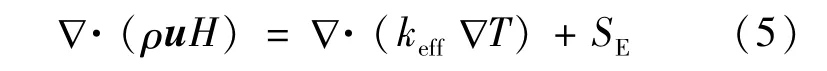
式中:H 是焓,J/kg;keff是有效导热系数,W/(m·K);SE是能量源项,本文为0。
模型采用焓—多孔介质法模拟钆液的凝固过程[12],糊状区被处理成一种多孔介质。材料的焓H为:

式中:href是参考焓,J/kg;Tref是参考温度,K;cp是比定压热容,J/(kg·K);fl是液相率;L 是潜热,J/kg。
液相率fl可以通过固相线和液相线温度决定:

糊状区内孔隙度降低造成的动量和湍流下降分别为:

式中:Amush是糊状区常数,通常在105~ 108[13],本文设置为108;up是拉坯速度,m/s;φ 代表需要被求解的湍流量。
1.4 边界条件
模型使用的边界条件如图2所示。对于顶部钆液的入口和底部薄带的出口都使用恒定的速度入口(velocity-inlet)边界条件。底部薄带的速度即为结晶辊的转速,根据质量守恒即可通过入口和出口的面积计算出入口钆液的流速。入口温度设为浇注温度。
铸坯与结晶辊接触面设置为无滑移(no slip)的移动壁面(moving wall)边界条件,使壁面绕结晶辊圆心旋转,从而模拟结晶辊转动的过程,旋转角速度为2 rad/s;该壁面的传热边界条件设为对流,对流传热系数为8 000 W/(m2·K)。
铸坯与侧封板接触面设置为固定壁面(stationary wall)边界条件,传热也设置为对流传热,对流传热系数为300 W/(m2·K)。
液面设置为绝热、零剪切的固定壁面。水口壁面设置为绝热、无滑移的固定壁面。模型的中心对称面采用对称(symmetry)边界条件。
1.5 材料属性
模型研究对象为单质钆,材料属性如表2所示。

表2 单质钆的材料属性Table 2 Material properties of elemental gadolinium
1.6 计算流程
本数学模型通过ANSYS Fluent计算流体力学软件进行求解。模型采用SIMPLEC算法进行压力-速度耦合。由于模型涉及结晶辊的快速旋转和铸坯的弧形拉坯过程,因此分两步计算来提高模型的收敛性。第一步,将钆液入口和出口的速度、辊壁的旋转速度以及拉坯速度都设置为零,计算0.25 s,使辊壁上生成稳定厚度的凝固坯壳。第二步,开启钆液入口和出口的速度、辊壁的旋转速度以及拉坯速度,开始计算拉坯过程,直至熔池内的流场、温度场和凝固坯壳都达到稳定状态。
2 模拟结果与讨论
2.1 熔池内的流动特征
图3为浇注温度分别为1 673、1 698和1 723 K时窄面对称面(左)和宽面对称面(右)上的流速和迹线分布。钆液从水口流入熔池,冲击到辊壁后流速迅速衰减至0.06 m/s以下,部分钆液形成回流区,而其余部分则向下流动。最大速度区域出现在辊壁附近的凝固坯壳上,这是坯壳随辊壁一起快速移动导致的。在宽面对称面上,回流区出现在上部水口主流股旁边,其余流股则向下流动,在碰撞到底部凝固前沿后向周围扩散;底部凝固区随辊壁向下运动,速度达到辊速0.1 m/s。在窄面对称面上,顶部液面下方主流股旁形成了两个回流区。这是因为主流股冲击辊壁后,向上回流的流股在冲击到液面后分成两个流股,分别往水口和辊壁方向流动,从而形成两个转向相反的回流区。在窄面下部也形成了一个窄的回流区,这是向下运动的流股冲击到凝固前沿导致的。

图3 浇注温度分别为1 673(a)、1 698(b)和1 723 K(c)时窄面对称面(左)和宽面对称面(右)上的流速和迹线分布Fig.3 Velocity and streamline distributions on the symmetry plane of narrow face (left)and wide face(right)at the pouring temperatures of 1 673(a),1 698(b)and 1 723 K(c)
3种不同浇注温度下的流动模式基本相同,但也存在一定的差异。首先,随着过热度的增大,凝固区缩小,底部速度为0.1 m/s区域的面积依次减小。其次,凝固区的缩小也导致钆液流动的空间增大,有利于流场的发展,导致主流股旁的回流区面积依次增大。此外,在浇注温度1 723 K下,宽面对称面上主流股下方靠近薄带出口区域的流动与1 673和1 698 K对应的流动有所不同。这是因为1 673和1 698 K两种浇注温度下薄带出口附近区域已完全凝固,阻碍了钆液的流动;而1 723 K浇注温度下主流股下方区域的钆液在薄带出口区域没有完全凝固,钆液仍可向下流动。
浇注温度分别为1 673、1 698和1 723 K时液面的流速分布如图4所示。流速整体呈现从左侧辊壁向右侧熔池中心区域逐渐降低的特征。辊壁附近区域,辊壁的快速运动和回流流股共同作用导致流速最大,达到了0.05 m/s以上。水口附近区域在回流流股的作用下形成了一个流速大于0.025 m/s的区域。窄面对称面中部区域,在两个反向流动的回流区作用下形成了一个小死区。在宽面对称面与侧封板相交的区域,由于离水口较远,难以受到回流流股的影响,因此形成了一个较大面积的死区。
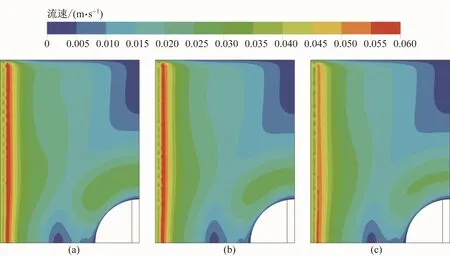
图4 浇注温度分别为1 673(a)、1 698(b)和1 723 K(c)时液面的流速分布Fig.4 Velocity distributions on the liquid level at the pouring temperatures of 1 673(a),1 698(b)and 1 723 K(c)
3种不同浇注温度下的流动模式完全相同,但浇注温度升高,凝固坯壳依次减薄,使流股更容易向下方流动,往液面回流的流股动能减小,造成液面流速依次减小。
2.2 熔池内的传热规律
图5为浇注温度分别为1 673、1 698和1 723 K时铸坯中心对称面和液面的温度分布。温度分布呈现从水口向四周以及沿拉坯方向逐渐降低的规律。在同一水平面上,水口下方区域的温度高于侧封板附近区域。受结晶辊强制冷却的影响,同时熔池通过侧封板向外界传递的热量很少,窄面对称面上的温度梯度远大于宽面对称面。

图5 浇注温度分别为1 673(a)、1 698(b)和1 723 K(c)时铸坯中心对称面和液面的温度分布Fig.5 Temperature distributions on the symmetry planes and the liquid level at the pouring temperatures of 1 673(a),1 698(b)and 1 723 K(c)
3种不同浇注温度下的温度分布规律完全相同,但浇注温度升高显著提高了熔池的整体温度,使凝固坯壳厚度减小。
浇注温度分别为1 673、1 698和1 723 K时铸坯与结晶辊和侧封板接触面以及出口处的温度分布如图6所示,呈现从内部往辊壁以及沿拉坯方向逐渐降低的规律。由于结晶辊的传热速率远高于侧封板,铸坯与结晶辊接触面的温度明显低于铸坯与侧封板接触面的。

图6 浇注温度分别为1 673(a)、1 698(b)和1 723 K(c)时铸坯与结晶辊和侧封板接触面以及出口处的温度分布Fig.6 Temperature distributions on the interface of strand and casting roll,the interface of strand and side dame,and the outlet at the pouring temperatures of 1 673(a),1 698(b)and 1 723 K(c)
3种不同浇注温度下的温度分布规律相似。浇注温度升高明显提高了铸坯的表面温度。此外,在铸坯与结晶辊接触面的右侧区域,浇注温度升高,高温区的面积依次增大,同时沿拉坯方向的温度梯度依次减小。这是因为随着浇注温度的升高,凝固坯壳减薄,水口高温流股对铸坯表面温度的影响直接体现在了铸坯表面上。
2.3 熔池内的凝固行为
图7为浇注温度分别为1 673、1 698和1 723 K时中心对称面处凝固坯壳沿拉坯方向的生长规律。首先,在距弯月面3~9 mm区域,坯壳厚度快速增加;然后,在水口主流股的直接冲击下,凝固坯壳沿拉坯方向先是有所减薄,随后较缓慢地稳定生长,直至在出口附近区域与另一侧辊壁上的坯壳啮合;最后,完全凝固的坯壳被结晶辊轧制成2 mm厚的薄带。
凝固终点的位置对于铸轧过程的顺利进行至关重要。如果凝固终点位置低于出口处,则凝固坯壳过薄,有引起漏液的风险;如果凝固终点位置高于出口处且距出口较远,则会产生表面裂纹、轧制力增大、结晶辊磨损增加等诸多问题。对比图7中3条曲线可以看出,浇注温度升高,凝固坯壳明显减薄。1 673和1 698 K对应的铸坯分别在距出口6.39和1.11 mm的位置就已经完全凝固;而1 723 K对应的铸坯在出口处仍未完全凝固,使薄带在出结晶辊区域时存在液芯,同时坯壳温度高,强度低,容易在拉应力的作用下断裂,发生漏液。此外,1 698 K对应的凝固终点非常接近出口位置,若浇注过程发生波动,则很可能在出口处难以完全凝固。因此,过高的浇注温度不利于铸轧过程的顺利进行,1 673 K对应的凝固坯壳厚度分布最为合理。

图7 浇注温度分别为1 673、1 698和1 723 K时中心对称面处凝固坯壳沿拉坯方向的生长规律Fig.7 Growth law of solidifying shell along the casting direction on the symmetry plane at the pouring temperatures of 1 673,1 698 and 1 723 K
图8为浇注温度分别为1 673、1 698和1 723 K时侧封板处凝固坯壳沿拉坯方向的生长规律。与中心对称面处不同,侧封板处受钆液流动的影响很小,因此凝固坯壳较为均匀、快速地生长,直至完全凝固,被轧制成2 mm厚的薄带。

图8 浇注温度分别为1 673、1 698和1 723 K时侧封板处凝固坯壳沿拉坯方向的生长规律Fig.8 Growth law of solidifying shell along the casting direction on the side dame at the pouring temperatures of 1 673,1 698 and 1 723 K
浇注温度升高,凝固坯壳明显减薄。1 673、1 698和1 723 K 3种浇注温度对应的凝固终点分别距出口8.26、5.41 和3.89 mm,铸坯均能在出口前完全凝固。
3 结论
(1)浇注温度从1 673 K升高至1 698 K再至1 723 K,凝固区面积减小,有利于流场的发展,从而增大了回流区面积,减小了液面流速。
(2)浇注温度升高,铸坯温度分布规律基本相同,但是显著提高了整体铸坯温度,同时水口高温流股显著提高了冲击位置附近区域的表面温度。
(3)浇注温度升高,凝固坯壳减薄,凝固终点位置下移。1 723 K对应的铸坯在中心对称面出口处未完全凝固,容易发生漏液;1 673 K对应的铸坯在中心对称面和侧封板处的凝固终点分别距出口6.39和8.26 mm,分布最为合理。
(4)稀土金属钆在结晶辊转速为0.1 m/s和浇注温度为1 673 K的条件下,可以获得较合理的凝固坯壳厚度分布。
