基于向量矩阵的Apriori 改进算法研究
2022-03-25裘慧奇
裘慧奇
(上海理工大学 信息化办公室,上海 200093)
人们的行为习惯对经济、社会、工作及生活等各方面的影响是学者们努力研究和探索的一个热点。与此同时,大数据伴随着物联网、云计算和人工智能技术的不断发展,在很多领域得到了应用和发展,为研究各行各业的用户画像提供了基础数据来源。如何利用大数据对用户行为进行分析,是数据挖掘技术在用户行为分析应用上的一个研究难点。关联分析是数据挖掘领域较为基础的数据处理方法,利用关联规则,从目标数据对象中挖掘出不同元素之间有意义、有价值的规则,从而发现目标数据集中的潜在数据模式和内在联系[1]。
近年来,信息技术在高校学生管理中的应用越来越广泛,学生的校园活动轨迹也被各类物联网设备和信息系统记录,如食堂消费、门禁进出、上课考勤、图书借阅及上网记录等,通过这些系统的数据记录,为基于数据挖掘技术的学生在校行为分析创造了条件。寻找关联规则是关联分析的核心,通过找出频繁项目集,并在频繁项目中找出隐含规则,是一种在大量数据中发掘某种潜在规律的数据分析方法,可以挖掘出数据之间有价值的关联关系。应用关联规则最经典的例子是啤酒尿布购物习惯挖掘[2]。利用高校学生的行为轨迹数据集,挖掘学生行为与学业水平之间的关系是高校在学生培养上利用大数据的一个经典应用场景。通过整合学生在校行为数据,运用关联规则方法进行数据挖掘,构建学生在校行为模型,从而实现对在校学生的行为预测,对学业水平进行预警,关注学生心理健康问题。本文结合在高校学生管理过程中的实际经验,在利用学生行为大数据分析时,对经典Apriori 算法进行了改进,在保持原有算法的有效性的基础上,改进算法大幅提升了关联规则挖掘的效率。
1 Apriori 算法及性质
Apriori 算法[3]是挖掘海量数据中的关联规则的一个经典算法,通过Apriori 算法,在事务集D中寻找满足所有最小支持度阈值的频繁项集;利用频繁项集生成所有满足最小置信度阈值的强关联规则,从而发现项目间的关联关系。
1.1 Apriori 算法的定理
定理1若一个项集不是频繁项集,则该项集的所有超集也不是频繁项集[4]。
定理2频繁项集的所有非空子集仍是频繁项集。
Apriori 算法利用定理1,通过连接产生候选项集。对候选项集进行剪枝产生频繁项集,采用逐层搜索的方法,由频繁k项集来构造候选k+1 项集,当没有新的候选项集产生时,生成最终频繁项集。算法虽然简洁,但需要进行大量的计算。主要存在如下2 方面问题:
a.生成的候选项集数过多,尤其是候选2-项集。如频繁1-项集的数目为n,则会产生个候选2-项集使内存占用很大;
b.扫描数据库的次数过多,每次更新支持度的时候都需要重新扫描数据库,需要很大的I/O 负载,在时间、空间上都需要付出很大的代价。
1.2 算法相关符号说明
I表示关联分析事务数据库的事务项,由事务数据库中的项组成。
T表示事务项I的事实组合。
Lk-1(i-1)集合表示由Ii组成的k-1-i项目集,i∈(1,k-1)。
sup(Cj) :sup(Ci)=Nj/ |D|表示为项目Cj的支持度,j∈[1,i]。其中,Ci为事务项的向量矩阵,Nj为Ij在T({Ij})中出现的次数,|D|为事务项集数。
1.3 Apriori 算法的性质
性质1对于频繁k-1 项集的集合Lk-1,如果频繁项集中的集合个数|Lk-1| <k,则算法结束。
性质2Lk-1中任意2 个频繁k-1 项集自连接后组成的频繁k项子集为频繁项集的必要条件:Lk-1中任一频繁集必须满足前i个项的数目至少为k-i个。
证明由Lk-1(i-1)集合生成Lk-项集的集合Ck时,包 含k-项 集X={Ii},i∈[1,k],且 当|Lk-1(i-1)|<k-i时,k-项目X不是频繁k-项目集。其中,|Lk-1(i-1)|表示k-1 频繁项集的集合Lk-1同时包含项I(i)的个数,i=1,2,···。
假设上述Ck中,X为频繁k-项集。根据排列组合可得,也就是可以合并构成一个k-1 频繁项集。由X生成的k-1 频繁项集个数为k-i,即|Lk-1(i-1)|=k-i,与假设矛盾,由此得出:Lk-1中任一频繁集必须满足前i个项的数目至少为k-i个。
利用以上性质,在自连接之前对Lk-1进行一次枝剪,减少自连接的频繁项集数,从而实现降低候选频繁集频度计算的时间复杂度,提高运行效率。
2 Apriori 改进算法设计
由于Apriori 算法需要大量计算,尤其是对海量数据进行关联分析时效率不高,研究者通过改变数据的原始存储方式和数据表达结构这两方面进行算法优化和改进。文献[5]提出的I_Apriori 算法通过映射数据结构存储事务数据库的方法达到减少扫描数据库、降低计算复杂度的目的。文献[6]提出的Bloom_Apriori 算法利用布隆函数过滤压缩k-项集,精简事务集和候选集以提升挖掘效率,节省计算资源。文献[7]提出的FP-growth 算法利用FP-tree 精简事务数据库及候选集来减少枝剪次数。上述文献的算法都存在不足之处:计算过程中存储了大量与频繁项集无关的元素,同时存在重复扫描矩阵列或事务项集的情况。
根据Aprior 算法的性质,本文提出了一种利用〈key,valuses〉键值转换事务项集的方法对Apriori 算法进行改进。利用〈key,valuses〉键值表示将事务数据库映射为一个向量矩阵,用行向量来表示每一个项在事实事务组合Ti中的出现情况,‘1’表示存在,‘0’表示不存在。通过动态地分配内存进行I/O 存储,根据向量操作规则,只需要进行向量“与”运算就可以快速产生频繁项集。Apriori 改进算法在连接生成新的候选集后,直接进行交集运算即可得到支持度,省去剪枝过程中的反复比较,从而优化计算复杂度。
Apriori 改进算法利用向量矩阵数据库,减少扫描数据库次数和存储空间,利用向量“与”操作实现对连接和枝剪步骤的优化,从而降低了候选频繁集频度计算的时间复杂度,提高了运行效率。Apriori 改进算法优化关联规则挖掘的步骤如下:
步骤1重构事务数据库为向量矩阵,并计算1-频繁项集集合L1以及1-频繁项集集合L1对应的〈key,valuses〉值。
扫描数据库一次,将事务项目数据库转化为项目事务数据库。记录每个1 项集出现的记录,统计项目数,根据最小支持度删除不满足的项集,转换为基于〈key,valuses〉的频繁项集GetMrItem,从而转换生成新的事务项集合;
扫描数据转换为向量矩阵项目集合C={C1,C2,···,C(i)},并计算各项目成员在所有事务中出现的次数,分别为N1,N2,···,N(i)。
步骤2计算满足最小支持度的k-项集,通过“与”运算,生成k项频繁项集。
采用Apriori 算法的连接,利用“与”运算求连接项目的记录交集,生成新的记录数据库。
计算各项目支持度并与预设最小支持度min_support 进行比较,所有支持度sup(Cj) 大于预设最小支持度的项集合便为频繁k-项集集合Lk-中各元素对应的事务集合T({Cj}),可构建得到频繁k-项集集合Lk-对应的项集。
步骤3重复步骤2,直到不再产生满足最小支持度的项集为止,生成满足条件的频繁项集。
整个计算过程避免重新扫描原始数据库,而且生成的频繁项目集越多,扫描的数据库就会越小,从而提高了运行效率。若T中含有n个项集,则会生成2n-1 个候选项集,通过Item-Tidlist列表方式可以生成1-频繁项集,删除所有事务T中不含1-频繁项集生成新的事务T′,T′中 含有n′个项集,且n′≤n,可得 2n′-1 明显小于 2n-1。从而减少了候选项集数量。
Apriori 改进算法流程伪代码:

3 Apriori 改进算法实例分析
已知事务数据库D,如表1 所示,包含5 个项数的6 个事务,需要计算最小支持度为3 的频繁项集。

表1 事务数据库DTab.1 Transaction database D
步骤1对Ti求每个事务项对应键值,合并所有T键值,得到下述事务项对应的键值:
〈A,2〉,〈B,2〉,〈C,5〉,〈D,4〉,〈E,5〉,根据最小支持数阈值,生成频繁1-项集的集合L1:{〈C,5〉,〈D,4〉,〈E,5〉}。同步转换事务数据库D为向量矩阵D′,如表2 所示。

表2 向量矩阵D′Tab.2 Vector matrix D′
步骤2转换后的向量矩阵由行向量A=(1,0,0,0,1,0),B=(1,1,0,0,0,0),C=(0,1,1,1,1,1),D=(1,0,1,0,1,1),E=(1,1,1,1,1,0)组成;对L1中所有候选项集中的行向量进行组合“与”操作。即=(0,0,1,0,1,1),D∧E=(1,0,1,0,1,0),C∧D∧E=(0,0,1,0,0,1),并计算支持度,结果如表3 所示。

表3 候选项集“与”操作Tab.3 Results of “and” operation between candidate item set
根据Apriori 算法的性质2,得到频繁项集L2为{{C,D},{D,E}}。根据Apriori 算法的性质1,L2中项集个数等于2,小于3,因此,不再求频繁3-项集,最大频繁项集为频繁2-项集,即频繁项集。
4 实验结果与分析
4.1 实验数据处理
为了利用高校学生行为数据集对本文算法进行算法的有效性和高效性验证,需对现有数据进行预处理。为了挖掘学生在校行为习惯与其学业成长之间的隐含关联关系,仅仅对散落在各个业务系统的数据进行归集还无法直接利用关联分析算法进行挖掘分析[8],需要进一步清洗、转换和整合生成数据挖掘分析的样本数据。为了达到Apriori算法对数据样本的要求,需要对归集上来的样本数据进行离散化处理。本文采用了一种自动调整宽度的数据离散化方法[9]。经实践证明,该方法比较符合高校对学生管理的大数据处理要求。
将数据项属性值域划分N个类别,每个类别分别对应一个连续数据区间,区间的宽度由该类别的数据占整个数据区间的比例确定。数据项属性值域的类别数量及占比采用经验值法[10]确定,根据实际工作经验确定不同数据项的属性值域划分,充分考虑数据项的内在特点和差异,具有较强的灵活性。
本文选取笔者所在高校一个年级学生(4 400人)一周年系内系统产生的统计数据共计6 054 622条记录为样本。包含4 个维度(图书馆进馆记录、无线上网记录、早餐就餐记录、学习成绩),以刷卡进图书馆的信息作为学生去图书馆的依据,以早上8:00 以前的一卡通消费流水作为学生早起的依据,以Wifi 上网日志作为学生上网行为的依据,以该年级学生一学年内选修的52 万门课程考试成绩作为评价学生学习成效的依据。对学生访问图书馆次数、上网次数、早餐次数参照数据离散化方法中的第一种方法分别离散为6,5,5 个区间;学习成绩以不及格课程数量作为离散区间进行预处理[11],最终离散为10 个区间。同时去除学生基本信息以保护学生隐私,形成以年级学生数为样本事务数的数据库BehavioTtrajectory DateSet。如表4 所示。
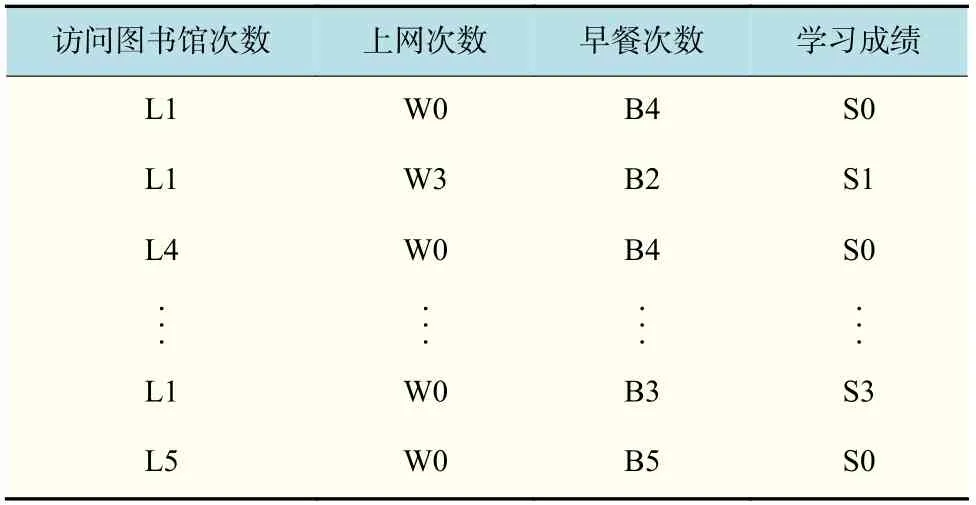
表4 样本事务数据库DTab.4 Database of sample transactions D
4.2 实验环境
以英特尔酷睿i5 2.9GHz 6 核CPU,DDR4 16G 内存,500GB SSD 硬盘配置的PC 为实验用硬件平台,部署Win10 操作系统,在Weka 开源平台设计实现。采用上述预处理数据集(学生在校行为数据集BehavioTtrajectory DateSet),共计6 054 622条记录来验证Apriori 改进算法的有效性[12]和高效性[13]。
4.3 结果与分析
为了验证Apriori 改进算法的有效性,对数据集BehavioTtrajectory DateSet 在相同最小支持度和置信度下分别用Apriori 改进算法和Apriori 算法进行关联规则分析,结果如表5 所示。

表5 相同最小支持度和置信度下频繁k-项集数Tab.5 Number of frequent k-item sets with the same minimum support and confidence
结果显示,在相同的支持度和置信度下,2 个算法计算获得的k-频繁项集数一致。因此,Apriori改进算法是有效可靠的,能够挖掘出准确的频繁项集。
对数据集BehavioTtrajectory DateSet 分别采用Apriori 改进算法、Apriori 算法、I_Apriori 算法、FP-growth 算法在不同最小支持度情况下的算法执行时间进行对比,结果如图1 所示。
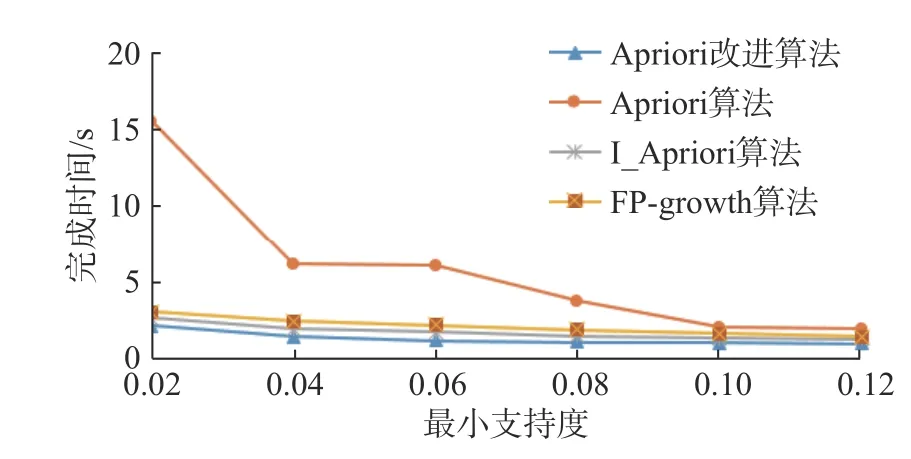
图1 BehavioTtrajectory DateSet 数据集实验结果对比Fig.1 Comparison of experimental results of Behavio-Ttrajectory DateSet
从图1 中可以看到,当最小支持度超过0.1 以后,Apriori 改进算法的效率基本与Apriori 算法一致。但是,当降低最小支持度时,会发现Apriori改进算法的效率明显高于Apriori 算法。这是因为Apriori 算法在产生频繁项集较多的情况下需要多次扫描数据库,导致I/O 负担过重,且存在大量无效的事务扫描,而Apriori 改进算法则通过扫描一次数据库即可获得频繁项集,在频繁项集较多时具有明显的性能优势,与本文改进算法的预期目标符合。
为了进一步验证Apriori 算法对潜在k-频繁项集数量的敏感性,将上述数据集进行分解,从中选择若干工科专业学生的行为数据进行关联分析,将数据集降为490 人,行为数据714 267 条为样本数据,项目数保持不变。对数据集Behavio-Ttrajectory-DateSet 分别采用Apriori 改进算法、Apriori 算法、I_Apriori 算法、FP-growth 算法在不同最小支持度情况下的算法执行时间进行对比,结果如图2 所示。

图2 BehavioTtrajectory-DateSet 数据集实验结果对比Fig.2 Comparison of experimental results of Behavio-Ttrajectory-DateSet
从图2 中可以看到,当数据集较小时,4 个算法对应最小支持度的敏感区间也相应地发生了变化,这是因为产生频繁k-项集的数量发生了变化。再次验证了影响算法性能主要是在计算大量频繁项集的阶段。
为了进一步验证改进算法的正确性,对同一数据集BehavioTtrajectory DateSet 在同一最小支持度和置信度的前提下,分别对Apriori 改进算法、Apriori 算法、I_Apriori 算法、FP-growth 算法比较生成频繁1-项集和频繁k-项集(k!=1)时的速度。在设定最小支持度为0.05、置信度为0.4 时,得到的频繁1-项目数为14 个,214-1 ≪226-1,实验证明,在样本数据中存在大量非频繁项时,本文算法性能体现出较大的优势。
从图3 中可以看到,4 个算法在生成1-频繁项集时所需时间基本相同,Apriori 改进算法所需时间略长,这是因为Apriori 改进算法在生成1-频繁项时,需要转秩事务项集数据库;但是,在后续k-频繁项集生成过程中,I_Apriori 算法、FP-growth算法较经典Apriori 算法性能有明显提升,其中,Apriori 改进算法性能优势更加明显。
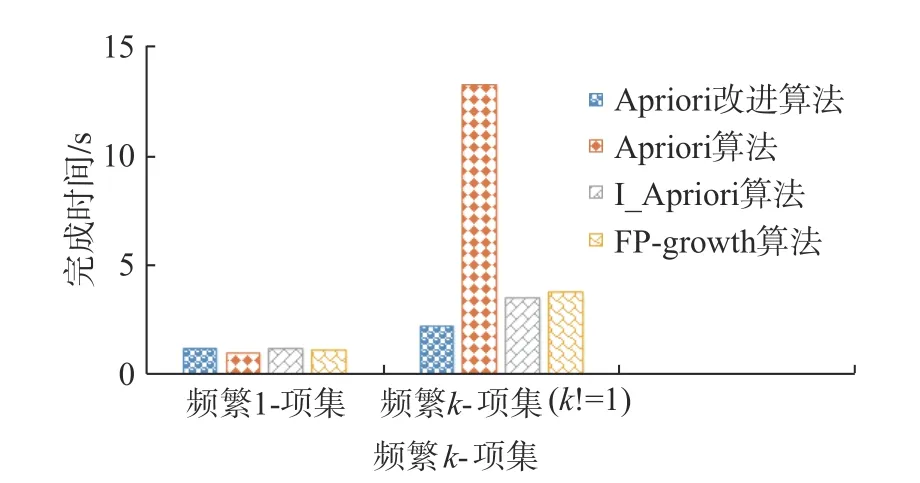
图3 生成频繁k-项集效率对比Fig.3 Efficiency comparison about generating frequent kitem set
4.4 算法应用分析
利用本文算法关联分析学生在校活动与学生成长的关系,为学校制定培养人才方案提供依据。以是否有早餐消费频次为判断学生是否有晚起习惯,以前往图书馆频次作为判断学生是否有自我约束能力[14],以上网频次来判断学生是否有网瘾,并根据以上维度来关联分析对学生成绩的影响。挖掘关联规则结果如表6 所示。

表6 在校活动与学生成长的关联规则Tab.6 Association rules between school activities with students' growth
通过调整最小支持度和最小可信度,在最小支持度为0.2、可信度大于60%的规则下产生强关联规则5 条,分析可得,有良好生活习惯、具有自我约束能力(定期去图书馆)的学生,学习成绩基本不挂科。
另外,分析有挂科情况的学生的行为习惯,将样本数据中无挂科学生的记录清除后进行关联分析,发现同样在最小支持度为0.2、可信度大于60%的规则下,习惯早起(有早餐消费习惯)的同学挂科数较少,且这类学生也会不定期去图书馆,对无线网络也不特别依赖。
5 结束语
Apriori 算法是经典的关联规则挖掘算法,但是,由于每次更新支持度时都需要重新扫描数据库,需要很大的I/O 负载,在时间、空间上都需要付出很大的代价。Apriori 改进算法通过转换事务项集的方法对Apriori 算法进行改进,在频繁项集求解过程中减少数据库的扫描次数,降低了I/O 消耗,利用向量“与”运算提高了运算效率。Apriori改进算法在连接生成新的候选集后,无需再进行枝剪即可直接取交集运算获取支持度,省去剪枝过程中反复比较,从而达到了性能优化的目的。同时,在验证Apriori 改进算法时,利用现实生活中的行为轨迹数据,通过数据预处理形成一个样本数据集,验证了Apriori 改进算法的有效性,又通过对比经典Apriori 算法及若干Apriori 优化算法验证了本算法的高效性。
