Landau 定理在高维复射影空间的推广

王 晗，刘晓俊

（上海理工大学 理学院，上海 200093）

1 问题的提出

设f:D(a,r)→C 全 纯，且对于所有z∈D(a,r)，f(z)≠0 且f(z)≠1。Landau 定理[1]断言:存在绝对常数A和B使得

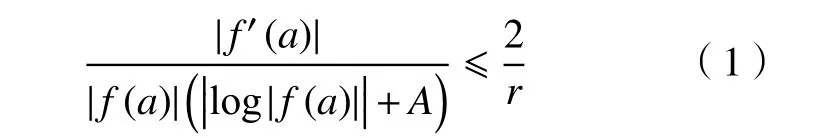
且

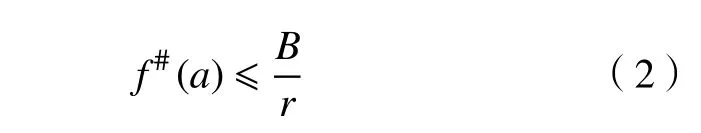
式（1）中常数A被称为Landau 常数。曾经有许多数学家致力于估计此常数A，1947 年Hayman[2]最早得出A的估计值，证得A≤5π。Jenkins[3-4]采用和Schottky 定理类似的方法在1955 和1956 年分别推出A≤7.77和A≤5.94。1960 年，Lai[5]对文献[3-4]中Jenkins 的方法稍加改进，得到=4.76···。在20 世纪70 年代末，首先由Lai[6]给出了A的精确估值：

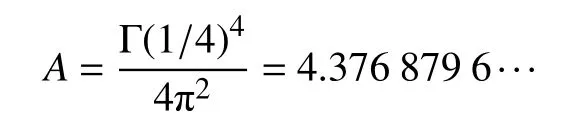
Hempel[7]和Jenkins[8]先后彼此独立地得到了相同的结果，他们所用的证明方法各有不同。尽管如此，Landau 定理的显示估计形式仍有改进的空间。

近年来，Cherry 等[9]建立了单位圆盘到高维复射影空间中全纯曲线的Landau 定理，得到定理1。

定理1设H0,···,H2n为 Pn上 2n+1个位于一般位置的超平面，设

受定理1 的启发，本文研究上述问题。若将条件改为：设f:Δ →Pn(C)为 全纯曲线，D1,D2,···,D2t+1为 Pn(C)上 的 2t+1个 位于t-次一般位置的超曲面，结合Zalcman 引理[10-11]得到类似的结果。

定理2设f:Δ →Pn(C)为 全纯曲线,D1,D2,···,D2t+1为 Pn(C)上 的 2t+1个 超曲面 且位于t－次一 般位置。若对于每一个j=1,2,···,2t+1,f(C)不 取Dj,则存在绝对常数M使得

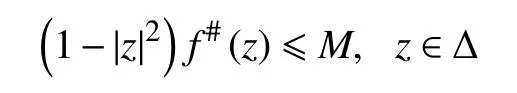
且

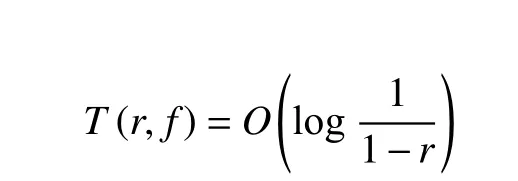
由此可得推论1。

推论 1设f:D(a,r)→Pn(C)为 全纯曲线，D1,D2,···,D2t+1为 Pn(C)上 的 2t+1个 超曲面且位于t－次一般位置。若对于每一个j=1,2,···,2t+1,f(C)不取Dj,则存在绝对常数M使得

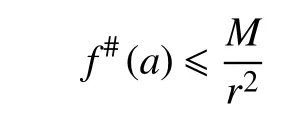
本文给出主要定理证明之前，先介绍一些符号。D(a,r)为 C 中的区域，表示以a为圆心、r为半径的圆盘。D(0,1)是单位圆盘，记作 Δ。其中，fn(z)⇒f(z)在D上 表示序列 {fn}按 照 Pn(C)上的富比尼-施图迪（Fubini-Study）度量在D上内闭一致收敛于f。对于定义在D内的全纯映射f(z)，f在 点z的球面导数记作。

2 定义及符号

特别地，M=Pn(C)时，即超曲面关于 Pn(C)处于t－次 一般位置也简称为处于t－次一般位置。关于Pn(C)处于n－次一般位置也简称为处于一般位置。

直观上说，超曲面D1,D2,···,Dq关于M处于t－次 一般位置是指，对任意的一点p∈M，至多存在这些超曲面中的t个在此点相交。

有两种方法将Nevanlinna 理论推广至全纯曲线上，分别是Cartan 利用对数导数引理的方法及Ahlfors 的负曲率方法。

设f:C →Pn(C)为全纯曲线，r＞0，定义f的Cartan-特征函数Tf(r)为

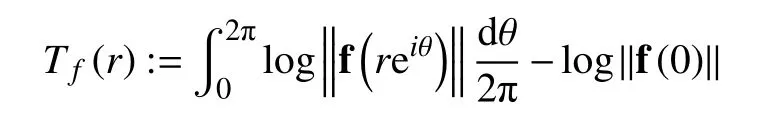
其中，f是f的一个既约表示。

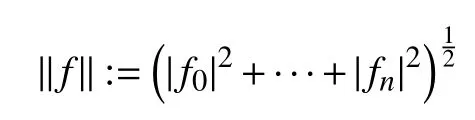
这个定义事实上与f的既约表示的选取无关。

定义f的Ahlfors-特征函数Tf(r)为

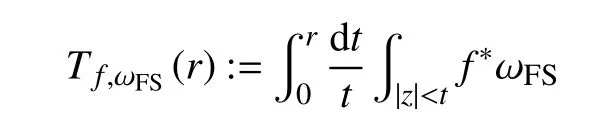
其 中，ωFS为 Pn(C)的Fubini-Study 度量的微分形式。这两种定义是统一的，事实上由全纯映射的Green-Jensen 公式，有

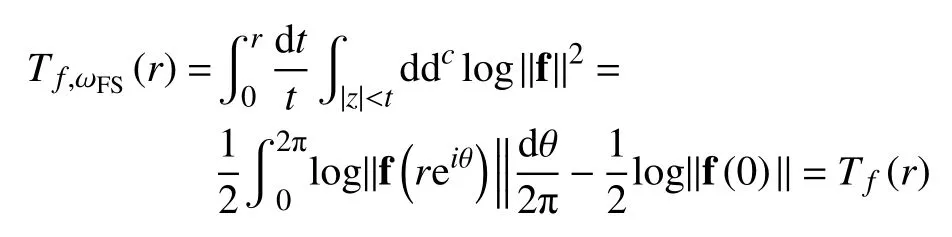
计算Fubini-Study 度量形式在全纯曲线下的拉回，则

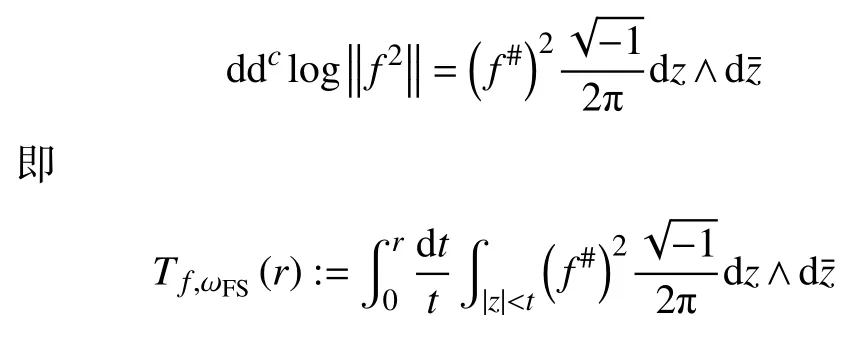
3 几个引理

众所周知，Zalcman 引理[13-14]为正规族理论中一个非常重要的引理，起着核心的作用。在给出主要定理的证明过程之前，需要如下关于从Ω ⊆C 到 Pn(C)的全纯映射的Zalcman 引理（引理1）。

引理1[13-14]设 F是一族从 C 上区域 Ω映到Pn(C)上 的全纯映射，F 在 Ω上不正规当且仅当存在子列 {fn}⊂F，点列 {zn}⊂Ω，且zn→z0∈Ω，正数列 { ρn}满 足 ρn＞0和 ρn→0，使得

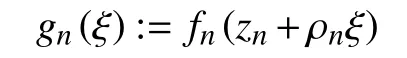
在 C的紧子集上一致收敛于从 C映 到 Pn(C)的非常值全纯映射g。

在主要定理的证明过程中，需要Picard 型定理（引理2）。

引理2[15]设f:C →Pn(C)为一条全纯曲线，其中，X是 Pn(C)中 的一个闭子集，D1,D2,···,D2t+1为 Pn(C)上 的 2t+1个超曲面，关于X处于t－次一般位置，若f(C)不 取Dj，或 者f(C)⊆Dj，j=1,2,···,2t+1，则f必为常映射。

4 定理的证明

4.1 定理2 的证明

证明倘若不然,则存在zn,|zn|∈Δ,使得

其中，g(ξ)是 C 映射到 Pn(C)上的非常数全纯曲线。

由于f(C)不 取Dj，j=1,2,···,2t+1，故由Hurwite定理可得g(C)不 取Dj，或g(C)⊂Dj，j=1,2,···,2t+1。由引理2 可知，g必为常映射，矛盾。定理2 得证。

存在M＞0，使得

结合式（3）和式（4），则

4.2 推论1 的证明