混合效应模型框架下反应时数据的分析： 原理和实践*

复旦大学外国语言文学博士后流动站/上海大学外国语学院 马 拯

上海交通大学外国语学院 贾锦萱 吴诗玉

提 要： 从分布形状、趋中度以及离散程度来看，反应时都具有区别于其他数据类型的非常鲜明的特点。因此，反应时数据的统计分析处理往往也有不同的技术要求和门槛。基于R语言的混合效应模型为反应时分布上的正偏斜、各数据点之间强关联以及异常值等问题提供了很好的解决方案。本文在回顾传统的反应时数据分析方法后，以一项具体的研究为实例介绍了使用“混合效应模型”来拟合反应时数据的基本原理、概念内涵以及如何拟合最佳模型等问题。

1. 介绍

反应时(Reaction Time, RT)，亦称作响应时间(response time)或反应潜伏期(response latency)，是以时间来计量(通常为毫秒)的一种简单或许也是应用最为广泛的对行为反应的测量，它一般指实验任务开始呈现到它完成的这段时间。最早在1868年，Donders做了一个具有开创意义的心理学实验，第一次使用反应时来测量人的行为反应，并提出一共存在三种长短不一的反应时，概括起来分别是(见Baayen & Milin, 2010： 13)： (1) 简单反应时。指经由被试对光、声音等刺激实验任务做出反应而获得的反应时间。(2) 辨识反应时。在收集这种反应时的时候，被试要同时面对两种实验刺激任务的挑战，一种是需要尽快做出反应的刺激任务，另一种则是需要忽略以免受其干扰的刺激任务。(3) 选择反应时。在收集这种反应时的时候，被试必须既快速又准确地从实验任务中所呈现的一系列可能的选项中做出一种选择，比如按键选择屏幕中出现的字母或单词。另外，也有的反应时是由这三种不同实验任务组合而成，亦可称作第四种反应时，比较典型的如区别反应时(discrimination reaction times)。在这种实验任务里，被试必须对同时呈现的两个实验刺激进行比较，然后按键做出选择，融合了(2)和(3)两种反应时的特点。

上述收集反应时的各种实验任务都基于一个共同的假设前提，即认知过程是需要时间的，通过观察和计算被试对不同的实验刺激任务做出反应或者在不同的条件下执行一项任务所需要的时间，可以认识大脑的工作原理等重要问题，并且对语言加工的认知过程或者机制进行推理(Jiang, 2012)。自Donders的开创性实验，尤其是20世纪50年代以来，反应时越来越来广泛地被实验心理学研究者所采用，并逐渐成为心理学和其他相关学科获取基于数据的人类认知制约模型的重要手段(Evans, 2019)。

在第二语言研究领域(包括二语或外语，以下简称二语)，无论是国际还是国内，研究者也都开始大量地使用反应时数据来研究第二语言的习得、理解和加工的心理认知过程，并取得了丰硕的成果。大量以反应时数据作为主要测量手段的研究论文发表于二语研究的各类期刊(见Jiang, 2012；吴诗玉等,2016)。值得简单介绍的是这一领域内研究者们在获取反应时数据时所使用的各种实验范式，因为它们集中体现了这一领域的最新发展概况以及这个领域学者们的创造性。最常见的有以下几种： (1) 词汇判断任务(Lexical Decision Task, LDT)。在这种任务里，被试看到屏幕上呈现一串字符串(既可以是英语的字母也可是汉语的汉字等组成)，需要既快速又准确地判断它是否是一个单词，电脑自动记录判断的时间，这种反应时主要综合了上述第一和第三种反应时的特点。(2) 单词或者图片命名任务(A Word or Picture Naming Task)。在这种任务里，被试必须大声朗读所看到的一个单词并尽可能快地同时为其命名，它综合了上述第一和第二种反应时的特点。(3) 自定步速阅读任务(Self-paced Reading Task)。在这种任务里，被试需要在电脑屏幕上阅读由实验者划分成的按一小节一小节(segment)方式呈现的文字(既可能是一个一个的词或者短语，也可能是一个一个的从句)，电脑自动记录每一小节的阅读时间。这种简单反应时反应了被试阅读时复杂的理解和加工过程。(4) 句子-图片匹配任务(Sentence-picture Naming Task)。在这种任务里，一般要求被试既快又准确地判断句子是否准确地描述了图片的内容。其他一些常见的任务还包括翻译判断任务(Translation Recognition Task)(见吴诗玉等,2017)以及跨通道启动实验(Cross-model Priming Experiments)(见吴诗玉等，2014)，等等。

反应时数据比较显著地受到实验任务特点的影响。比如，反应时的长度与实验任务的刺激强度成反比，即实验刺激强度越强，反应时越短；刺激越弱，则反应时越长(Luce, 1986)。除此以外，反应时还显著地受到被试特征的影响，典型的特征如被试的年龄、性别以及用手习惯。一般来说，更年轻的比更年长的被试反应更快。最后，实验的进程也会影响反应时，比如在实验刚开始的时候，被试的反应可能逐渐加快，但是随着实验持续时间的增长，被试变得更疲劳，反应也慢了下来。

从统计分析看，反应时数据在分布形状、趋中度以及离散程度方面都反映出区别于其他类型数据的鲜明特点。因此，反应时数据的统计分析往往也有别于其他数据类型的技术要求和门槛。本文将在梳理和总结已有文献的基础上，对反应时数据的特点进行分析总结，并在混合效应模型的框架下探讨反应时数据处理方法的原理和实践，包括数据转换、异常值处理等。

2. 反应时数据的特征分析

数据的特征很大程度上决定着对它们进行统计分析时具体应该采用什么方法，本文从三个方面对反应时数据的主要特征进行介绍，包括： (1) 反应时的分布；(2) 反应时各数据点之间的关系；(3) 反应时数据的异常值。

1) 反应时的分布

一般来说，我们在对一组数据进行描述的时候，会同时考察它们的形状、趋中度和离散度(Gravetter & Wallnau, 2017)。尽管在分布上，通过上述各种不同的实验任务和实验范式所获得的反应时会存在一些差别，但在大部分情况下，反应时数据的分布特点就如图1所示。

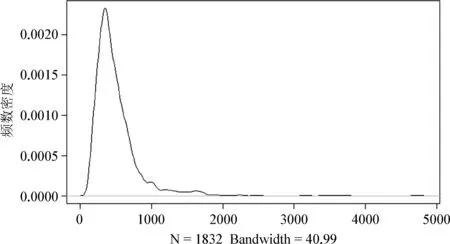
图1. 反应时数据的分布图(横轴表示反应时)

图1是我们通过自定步速阅读任务(见下文)收集到的40名中国大学生在阅读句子时所获取的句子内某一个片段所用时间的频数密度(density)分布图。可以看出，在分布上反应时明显地呈正偏斜(positively skewed)，即向右拖着一条长长的尾巴，并不符合正态分布的特点。除所有被试的整体反应时的分布呈正偏斜以外，每一名被试个体的阅读时间也具有相似的分布特点，图2呈现的是每一名被试阅读时间的分布(被试号分别为3、4、6、10、12、33、36、56、62)。

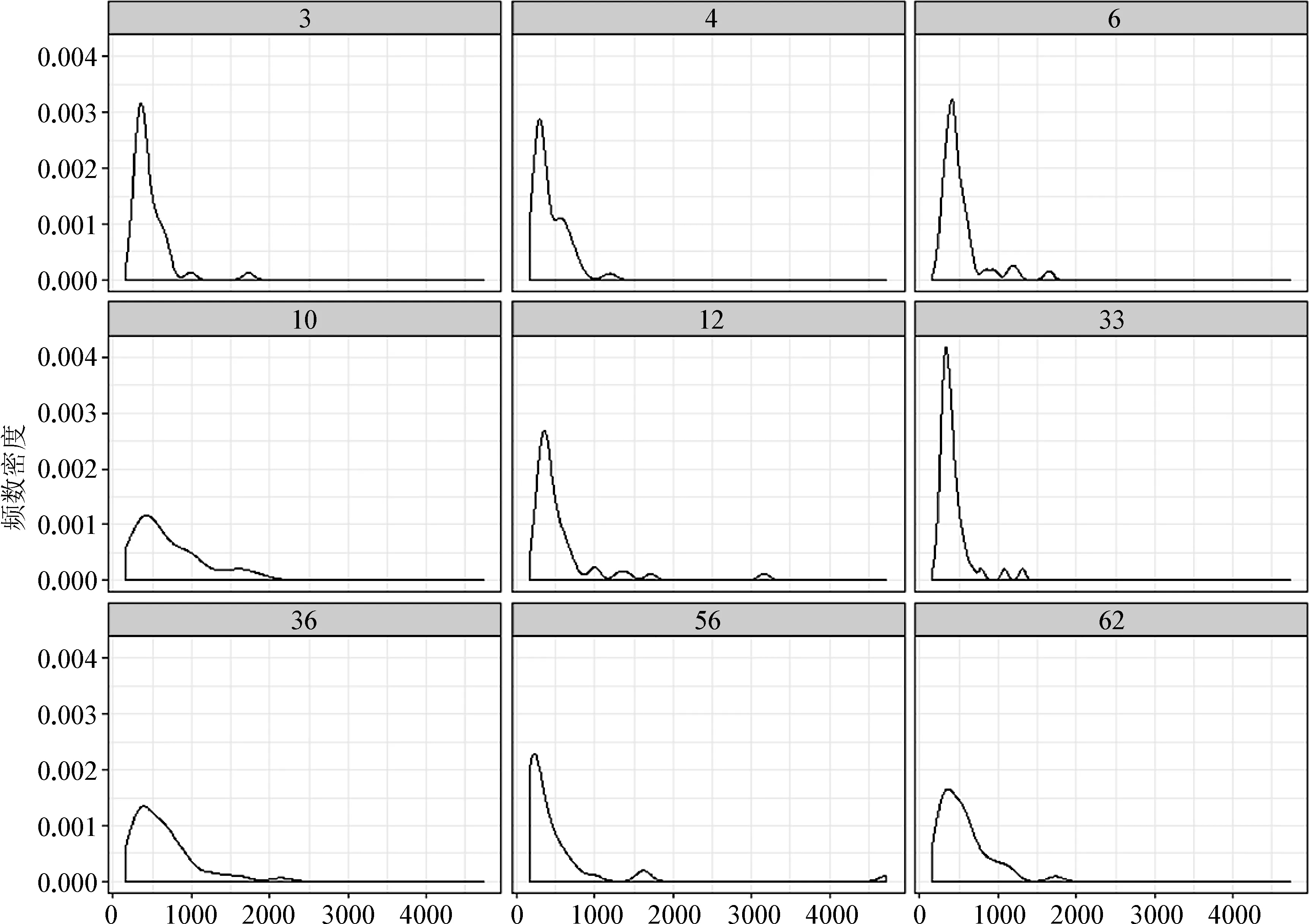
图2. 每名被试反应时分布图(横轴表示反应时)

从图2可以看出，每一名被试个体的阅读反应时间也体现出较为共同的特征，即呈正偏斜形态。我们在从样本的统计量对总体的参数进行推断时都是基于某种概率分布(如z分布、分布或分布等)，因此我们在拟合反应时数据的统计模型时常常会对它进行某种转换，从而让数据更符合某种概率分布的特点，对正偏斜的数据比较常用的转换方式是做对数转换(见Field, 2012; Winter, 2019；吴诗玉,2019)。比如，图3是对图1所示数据做对数转换后的分布形态，可以看出此时的反应时数据明显更接近于正态分布(如寺庙里悬挂着的一面大钟)。

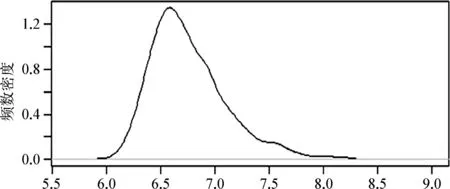
图3. 对数转换过后的反应时数据分布(横轴代表对数转换后反应时)

2) 反应时各数据点之间的关系

从实验设计上看，几乎所有的反应时实验任务都是重复测量被试内设计，即同一名被试参与了多个实验条件下多个测试项的测试，同时同一个测试项也应用在多个实验条件下对多名被试进行测试。先前的研究发现(de Vaan, 2007)，通过这种方法所获得的反应时数据具有一个非常明显的特征，也就是逐个反应时之间存在高度关联的关系(trial-by-trial dependencies)，亦称作自相关(autocorrelation)，即前后的反应时数据点相互关联。

反应时的这个特点跟我们大家所熟悉的一般数据，比如学生的考试成绩等有很大区别。一般的数据中各个数据点之间彼此独立或关联不大，比如学生A的考试成绩跟学生B的成绩并不会存在很强的关联。数据点之间彼此独立，是使用普通线性模型(generalized linear model)进行数据分析的基本前提(见Field, 2012; Gries, 2013; Winter 2019)。但是，通过重量测量被试内设计所收集的数据，比如同一名学生连续多次考试的成绩之间往往就会存在比较强的关联关系。在统计分析的时候，一般是通过进行球形假设(The Assumption of Sphericity) 来检验数据点之间是否相互关联。简单说来，球形假设是指实验的不同水平之间差异的方差必须大致相同，即如果把每个实验水平拿出来，然后计算每两个水平之间(即两两之间)的分数之差，这些差必须有大致相同的方差。可用以下等式简单表示：

Variance≈Variance≈Variance

对重复测量所获取的数据进行统计分析，一旦统计分组达到了三组或以上，就要考虑球形假设是否满足。不过问题是，虽然学术界已经有一些对球形假设不满足时的校正方法，比如Greenhouse—Geisser校正和Huynh-Feldt 校正，但是实际上到底该如何解决球形假设不满足时的校正问题却仍然存在很大的争议。这个问题给统计分析实际上带来了很大的困惑(见Speelman, 2018；吴诗玉,2019)。而如果无视球形假设是否满足，仍然对数据进行一般线性模型的拟合，就很容易犯统计学上的I类错误(Type I error)，即假阳性，本来不显著的结果却认为显著了。

3) 反应时的异常值

研究者收集反应时数据是希望通过它来反应被试的心理过程，但有的时候一些别的无关因素却可能导致反应时无法反应被试的心理过程，比如不小心按错键就可能导致出现非常短的反应时(低于250毫秒)。另外，被试也可能因注意力分散了或者疲劳、缺乏兴趣等而导致反应时特别长(见Jiang, 2012)。这些特别短或特别长的时间就称作为异常值(outliers)，在进行统计分析时必须先对它们进行筛选、鉴别和排除。

从统计模型的角度看，异常值一般包括三类： 离群点、强影响点和高杠杆值点(参见Kabacoff, 2015)。它们既有可能相同，也可能不一样。一般来说，离群点残差值很大，说明模型对它们的预测有很大的偏差，残差值如果是正数，说明模型低估了观测值，如果是负数则说明高估了。强影响点是指对模型的回归系数具有很强的影响力的点，若把这些点移除模型就可能发生很大改变，高杠杆值点是由许多异常的自变量值组合起来且与因变量没有关系的点。Baayen(2008)给过一个形象的比喻，他说就像一群羊，所有的羊都往北走，唯独有一头羊往西走，本来可以说羊群往北走，现在只能说羊群往西北方向走。唯独的往西走的那头羊就应该视为离群点，作为异常值对待。

学术界在处理异常值时比较常见的是把大于平均数2.5或3个标准差的数据去除，或直接把高于某个值比如2000毫秒的数据去除。这么做的根据是，在一个符合正态分布的一组数据中，大于平均数2.5或3个标准差的数据是“非常不可能”的(very unlikely)(概率极低，小于0.01)。但争议在于，如果反应时分布上总是偏斜的，那么这种“暴力、侵犯式”的数据删除就很容易导致数据损失，是数据科学家无法接受的事情(Baayen & Milin, 2010; Hsiao & Nation, 2018)。我们认为使用混合效应模型能有效地解决反应时的上述三个典型特征所带来的问题，下文着重介绍。

3. 混合效应模型

1) 历史传承

传统上，在分析反应时数据时一般是先计算两个平均数，再进行方差分析。第一个平均数以被试为随机因素，即1，计算每名被试在每个实验条件下所获得的反应时的平均数。比如，被试在4个实验条件下一共对48个刺激材料进行反应(见下文)，每名被试在每个条件下共对12个刺激材料进行反应，因此每名被试共可求得4个平均数。第二个平均数以刺激材料为随机因素，即2，计算每个测试项在每个实验条件下经过多名被试的测试所获得反应时的平均数。比如，48个刺激材料，在4个实验条件下，共40名被试参与了测试，这样每个测试项在每个实验条件共有 10名被试进行了反应，因此每个测试项共可求得4个平均数。在获得这些平均数后，再进行重复测量的方差分析，只有当1和2都显著的时候，才能判断一个自变量具有显著的效应(参见Clark, 1973; Forster & Dickinson, 1976)。

但是这一传统做法在今天开始变得有争议。首先，在一组呈正态分布的数据中，平均数的确具有代表性，但是鉴于反应时总是呈偏斜分布而且各数据点之间存在很强的关联，因此用平均数作为一组数据的代表忽视了被试或测试项个体差异。而实际上，在做行为实验时，个体差异是很常见的。如图4所示，有的被试总体表现比较平稳，比如A7和A8，但有的被试却存在很多变异，比如A10和A12。其次，只有当1和2都显著才能判断某个自变量的影响是否显著，可是在实际分析中，却常常碰到只有1显著或者只有2显著这种很“尴尬的情形”。第三，由于反应时数据点之间存在很强的关联性，除进行球形假设检验以外，解决方案之一就是把考察区域(如关键区)之前的区域的反应时以及材料的呈现顺序作为协变量进入统计模型，但是这给传统的重复测量的方差分析带来很大的操作难题，尤其是在使用SPSS软件进行分析的时候(参见Bayeen, 2008)。

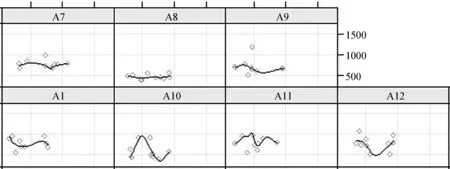
图4. 被试在完成测试时的个体变化

从2008年开始，解决上述问题的方法已经有了很大的变化，标志性的变化是Baayen等(2008)在国际著名的语言及认知期刊(JML)上发表的题为 “Mixed-effects Modelling with Crossed and Random Effects for Subjects and Items”的文章以及同年Baayen在剑桥大学出版的专著，它们专门介绍和论及了混合效应模型的内在机制以及具体的应用问题。自此，混合效应模型就开始在语言科学学术圈，包括应用语言学、心理语言学、社会语言学以及语料库语言学等广泛应用起来(见Bates., 2015;吴诗玉,2019)。

2) 概念内涵及操作

(1) 概念内涵

所有的统计程序根本上看都是相同的，可以概括为下面这个简单的等式：

outcome=(model)+error

它的意思是，我们观察到的所有数据都可以通过使用收集到的数据拟合的模型(即等式中的model)加上误差来进行预测(见Field, 2012： 41)。而这里所指的模型就是指基于数据而拟合的一个线性回归模型，也可以用下面这个等式表达：

Y=b+bXbX…+bX

在这个等式里，Y是指因变量，而X1, X2…等则表示自变量，b称作为截距(Intercept)，表示在X都等于0时的Y值。而b， b…等称为斜率(slope)或回归系数，它们表明了当X变化的时候，Y变化的程度，表征的就是实验中自变量对因变量的影响。斜率和截距是决定线性模型最重要的两个参数，统计分析根本上就是要对斜率和截距进行估计。

有了这些简单的知识以后，就可以解释何为混合效应模型，也称作为线性混合模型(Linear Mixed-effects Models, LMEM)，简称为混合模型(Mixed Models)。所谓混合模型就是指在一个模型里同时包含了固定效应因素(fixed-effects)和随机效应因素(random-effects)的模型。固定效应因素就是指在一个实验中水平是固定的并且可以在别的实验重复、复制的因素；而随机效应因素则是指通过总体抽样出来的，别的实验一般不能重复和复制的因素。一般比较常见的固定效应因素就是实验的操控变量(即实验干预)，而随机因素一般指实验的被试或者测试材料(Winter, 2019)。下面以一个具体实例来展示如何使用混合效应模型来解决上述反应时数据分析时会碰到的问题。

(2) 实际操作

先对即将应用的数据进行介绍。这是一个我们采用自定步速阅读收集的40名中国大学生在阅读48句如(1)所示的句子对(sentence pairs)时所获取的反应时数据。在实验时，句子按一个小片段一个小片段的方式呈现，每个句子对(如1a)中第一句话为语境句，交待指代物的数量(one vs. two)，第二句称作为目标句，其主语要么是一个光杆名词(那头奶牛)，要么是一个带有修饰语的名词(那头棕色的奶牛)(bare vs. modified)。考察的关键区是目标句主语的阅读时间(即目标句开头的小片段： 那头(棕色)牛)，目的是检验语境句中指代物的数量是否会显著影响目标句中关键区的阅读。一共获得1920(40*48)个反应时数据。由于自定步速阅读是学术界广泛采用的获取反应时数据的方法，因此，该实验的数据具有代表性(Marsden., 2018; Wu & Ma, 2020; 吴诗玉,2020)。

(1a) 农场上 /有/一头奶牛。

那头奶牛/躺在/田间。

(1b) 农场上 /有/两头奶牛。

那头奶牛/躺在/田间。

(1c) 农场上 /有/一头奶牛。

那头棕色的奶牛/躺在/田间。

(1d) 农场上 /有/两头奶牛。

那头棕色的奶牛/躺在/田间。

从设计上看，本实验一共有两个自变量： (1) 指代物的数量，简写为CONTXT，它有两个水平(one vs. two)；(2) 指称表达，简写为EXPR，也有两个水平(bare vs modified)。从混合效应模型的结构看，这两个自变量是固定效应因素，而实验中的被试和所阅读的句子则是随机因素。如果采用传统的方差分析，应该分别以被试和实验材料为随机因素，分别计算1和2，只有当它们都显著的时候，才能判断主效应或交互效应的存在。但是，正如上面所说，这种传统的方法会碰到三个很棘手的问题，即： (1) 反应时的分布呈正偏斜的特点；(2) 反应时各数据点之间高度关联；(3) 反应时异常值的处理。下面介绍如何使用R语言以及混合效应模型来解决这些问题。

首先，对于第一个分布呈正偏斜的问题，可以对反应时进行对数转换，如log(Y)。其次，关于各数据点之间高度关联的问题，就本实验来说，混合效应模型采用的是往模型里添加引起数据点之间关联的两个协变量来解决。第一个协变量是被试在阅读时材料的呈现顺序(表示为TRIAL)，一般来说，在自定步速阅读这种任务里，被试的阅读会深受所读材料的顺序影响。在实验刚开始，被试还没有适应或不熟练，阅读会比较慢，但是随着逐渐适应并变得熟练，会自然变快，但最后又可能因疲劳而变慢，因此只有把材料呈现顺序的影响进行控制，才能更准确地评估自变量对因变量的影响。第二个协变量是关键区之前的阅读时间，在本实验中，被试在阅读关键区之前已经阅读了三个区域(见(1))，这三个区域的阅读时间肯定会对被试当前的阅读时间造成影响，因此也必须对它们进行控制。但问题是之前一共有三个区域，这三个区域的阅读时间本身也可能存在高度关联，因此如果把它们都作为协变量进入模型，肯定会带来模型拟合的另外一个问题，即多重共线的问题。因此不是把这三个区域的反应时都同时放入模型，常规的做法是先对它们进行主成成分分析(Principal Component Analysis, CPA)，把获得的主成成份放入模型(参见Baayen, 2008)。使用lme4包中的lmer函数，一开始拟合一个最大模型，如下：

model1 <- lmer(log(RT)～ scale(TRIAL)+PC1+CONTXT*EXPR+

(1+CONTXT*EXPR|SUBJ)+(1+CONTXT|Items),

data=myData)

模型命名为model1，因变量为log(RT)，即经过对数转换后的反应时。scale(TRIAL)+PC1+CONTXT*EXPR 是模型的固定效应结构，其中TRIAL如上文所示表示阅读材料呈现的顺序，但是为了让结果容易解读并避免模型出现多重共线问题，把它进行标准化处理(即scale(TRIAL))，PC1表示的是对关键区之前的三个区域的反应时进行主成成份分析后所获得的第一个主成成份(总共只有三个区域，一般一个主成成份已经足够)，SUBJ表示被试，CONTXT*EXPR是两个固定因素的交互项。(1+CONTXT*EXPR|SUBJ)+(1+CONTXT|Items)是模型的随机效应结构，其中SUBJ表示实验的被试，Items是指阅读材料，使用的数据命名为myData。在拟合这个模型时，遵循了Barr等(2013)提出的“保持最大化”原则(keep it maximal)，即既考察被试(SUBJ)和阅读区域(Items)的随机截距，也考察它们的随机斜率。

除了通过加入协变量TRIAL和PC1来解决数据点之间的关联性以外，随机效应结构(即(1+CONTXT*EXPR|SUBJ)+(1+CONTXT|Items))通过捕捉各个被试之间以及各个实验材料之间的个体差异和变异也一定程度上控制了数据点之间的关联的影响。上文讲过，回归模型最重要的两个参数就是截距和斜率。但是为了同时模拟各种变异的来源，混合模型不是简单的对许多被试(或阅读材料)只拟合一条回归线，而是同时拟合每一名被试和每一个测试项(材料)的多条回归线。这些不同的回归线里都有特定被试或者特定测试项(材料)的随机截距(random intercepts)和/或随机斜率(见Gries, 2013： 333-334)，通过随机截距和随机斜率，混合模型真实地描述了每名被试和每个测试项在实验时所经历的各种变化(见Winter, 2018： 163)。

关于第三个问题，即反应时异常值的问题。混合效应模型分析数据一般包括三个步骤，即构建模型、对模型进行诊断和解读模型，混合模型正是通过模型诊断的方法来去除异常值，研究者把这个方法称作“最小先验删除法”(minimal apriori data trimming)(参见Wu & Ma, 2020)。它的思路是先把“根本不可能出现的”反应时去除，在此基础上拟合一个混合模型，然后进行模型诊断，把残差绝对值大于平均数2.5个标准差的数据去掉。“根本不可能出现的”反应时包括被试对理解问题回答错误的数据以及小于250毫秒的数据，因为一般认为，即使被试不受实验干预的影响做出反应至少也需要250—300毫秒以上。

在我们的实验中，初步拟合的上述“最大”模型出现了“不能收敛”(failed to converge)的问题，因此削减模型的随机效应结构，并尝试使用不同的优化器(optimizer)。根据“奥卡姆剃刀”原则(Ocam’s razor)，在两个模型具有相同解释力的基础上，选择更加简单的模型。经过操作后，获得以下“最佳模型”：

Model.eml <- lmer(log(RT)～ poly(scale(TRIAL),2)+PC1+CONTXT*EXPR+

(1 |SUBJ)+(1+CONTXT|Items),

data=myData,

control=lmerControl(optimizer=“bobyqa”,

optCtrl=list(maxfun=2e5))

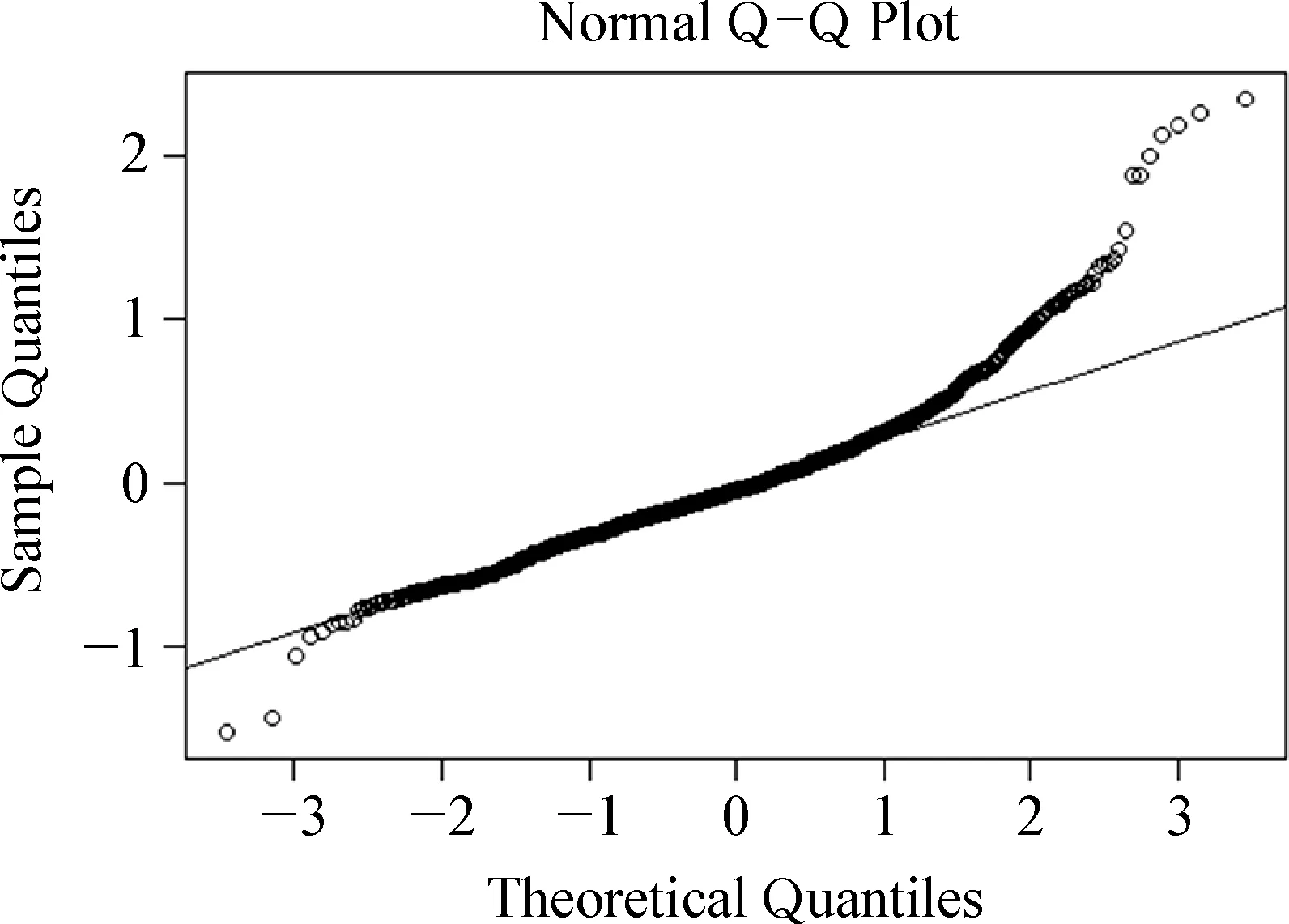
图5. 残差Q-Q分布图

与最初的“最大”模型相比，这个模型的随机效应结构简化了很多，查看模型残差的Q-Q分布图，获得图5。

一般来说，拟合得很好的模型的残差值应该呈正态分布，表现在大部分的点都应该与那根呈45度角的直线大致重叠。但是从图5可以看出，模型严重受到了异常值的影响，两端翘尾。因此去除残差绝对值大于平均数2.5个标准差的值，获得新的数据集，命名为newData：

newData <- filter (myData, abs(scale(residuals(Model.eml))<=2.5)

在newData的基础上，重新拟合模型，并获得最终模型如下：

Final.model <- lmer(log(RT)～ poly(scale(TRIAL),2)+PC1+CONTXT*EXPR+

(1 |SUBJ)+(1+CONTXT|Items),

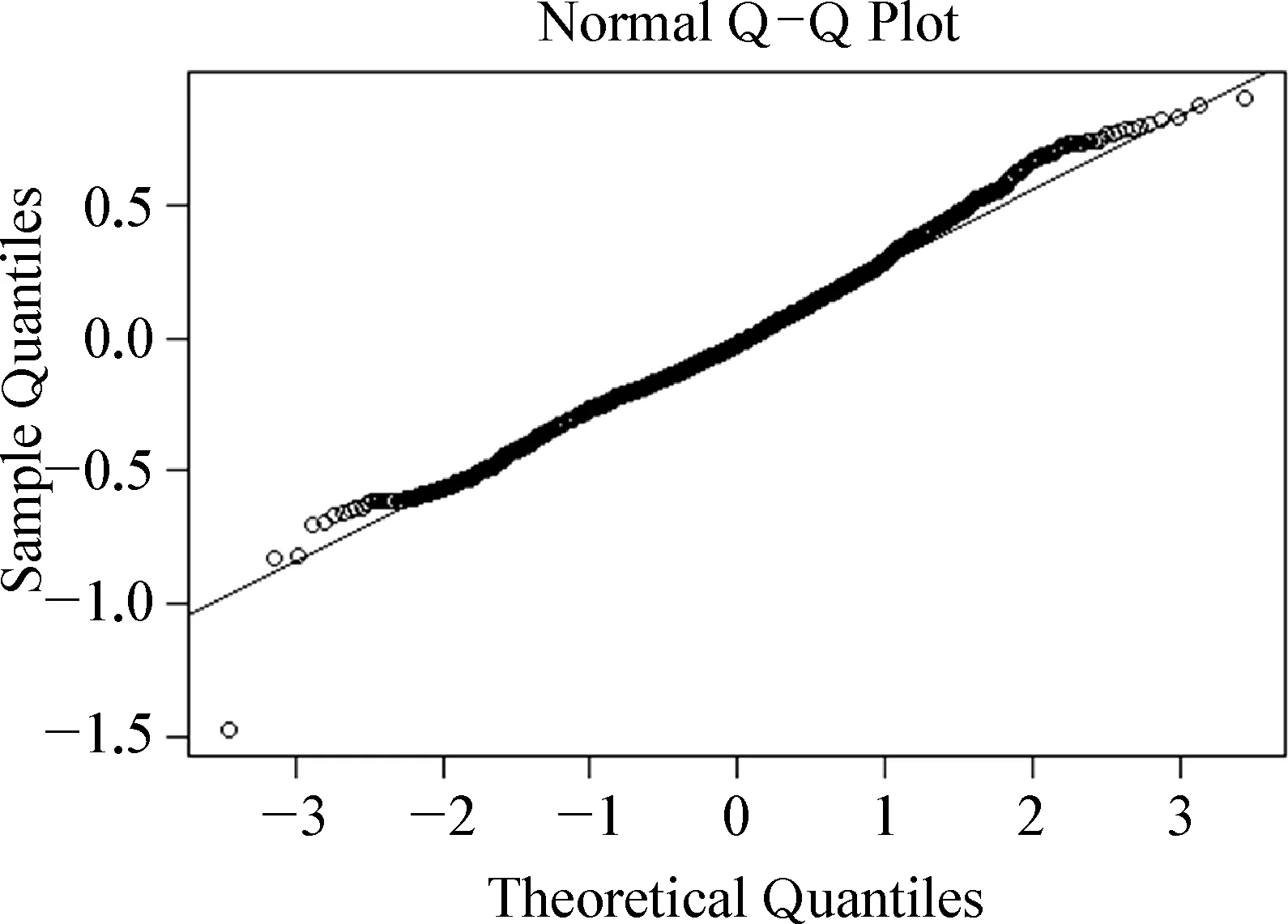
图6. 重新拟合后模型的残差Q-Q分布图

data=newData, REML=FALSE,

control=lmerControl(optimizer=“bobyqa”,

optCtrl=list(maxfun=2e5))

重新查看这个模型的残差Q-Q分布图6：

从图中可以看出，模型的拟合优度显著改善，在消除异常值对模型的影响后，残差值的分布达到几近完美的正态分布。表1展示了模型固定效应的结果。

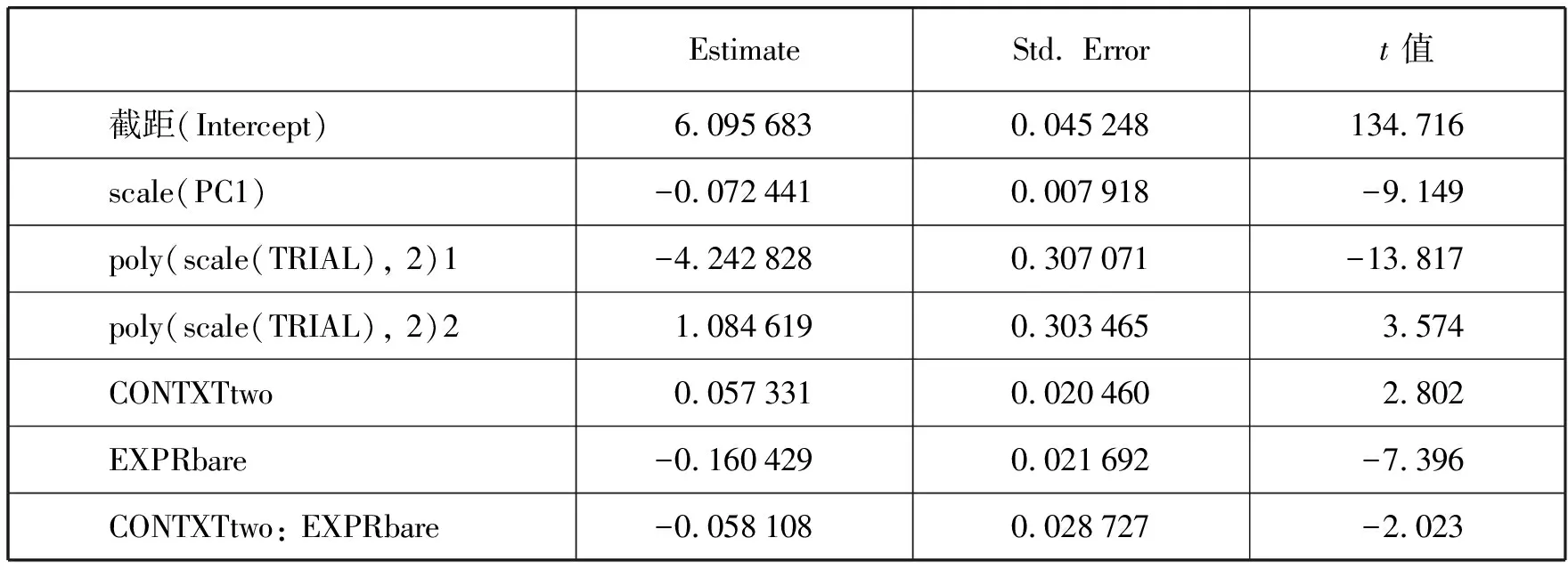
表1. 混合效应模型的回归系数(Estimate)、标准误(Std.Error)以及t值

一般认为，回归系数对应值的绝对值如果大于2就表示显著(Baayen, 2008)。表1的结果最值得注意的是，两个用来控制数据点之间关联性的协变量(即TRIAL和PC1)拥有最大的值，这个结果与先前一些研究的发现相一致(见Baayen2010)，充分说明对反应时数据进行分析时，对这些协变量的影响进行控制是非常有必要的，这既满足了模型所要求的数据点之间必须彼此独立的假设，也显著地提升了模型拟合的效果，让实验干预(即自变量的影响)的效果变得更加明显。此外，从上表还可以看出，两个自变量，即指代物的数量(CONTXT)和指称表达(EXPR)都有主效应，而且更重要的是两者还有显著的交互效应(β=-0.058,=0.03,=-2.023)，说明语境中指代物数量的影响还要取决于指称表达的类型。表2展示了混合模型随机效应结构的结果。

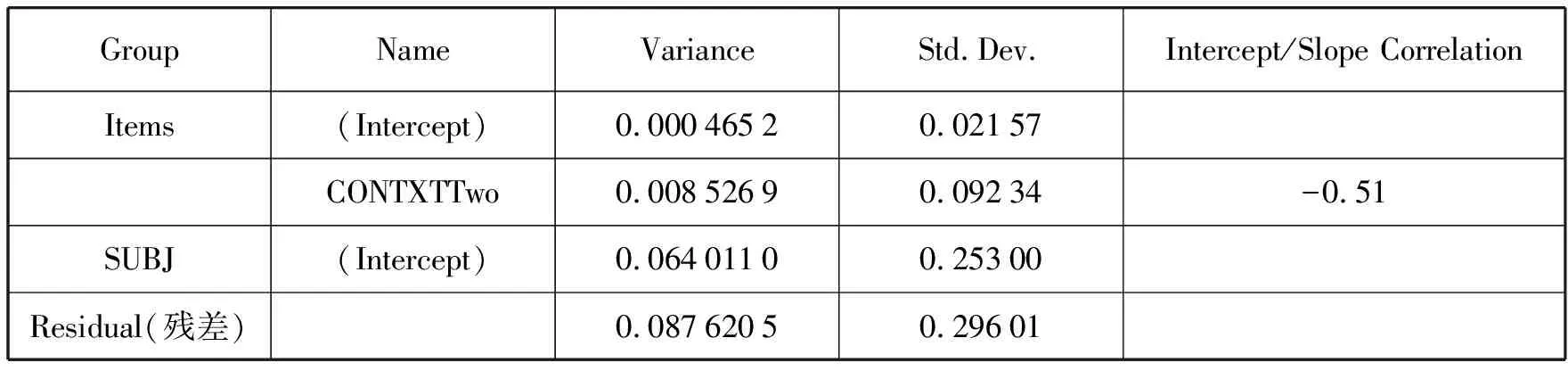
表2. 混合效应模型随机效应结构的统计摘要

从表2可以看出，一共有两个随机因素，即被试(SUBJ)和对应的阅读区域(Items)，表2分别呈现了这两个随机因素的方差(Variance)及标准差(Std.Dev)，从表中可以看出被试的标准差(0.25)要远远大于阅读材料的标准差(0.02)。这个结果符合心理语言实验的大部分情况，即被试是一个比实验材料更难控制的因素。此外，由于模型既考察了阅读材料的随机截距(Intercept)也考察了随机斜率(Slope)，因此表2还呈现了它们的相关性，在这个模型里相关系数为-0.51，表明如果阅读材料的截距比较大，材料的斜率就会比较小，说明如果一开始阅读材料被读得比较快，到后面速度可能会降下来，相反，如果一开始读得比较慢，到后面就可能会快起来。

4. 结语

反应时数据具有非常鲜明的特点，在对它进行统计分析时，要充分考虑它的分布、数据点之间的关联性以及异常值的问题。我们认为使用R以及混合模型可以比较好地解决这些问题。语言科学研究中的许多数据，包括心理语言实验所获得的重复测量的数据、语料库研究中的频数计数数据以及社会语言学以及类型学研究中的大量关联数据，都适合使用混合效应模型来分析。如果使用R来拟合模型的话，则还可以同时享用R强大的统计和数据可视化能力。倡导使用混合效应模型来拟合反应时数据，是提倡在验证研究假设、回答研究问题、分析多变量之间的关系时尝试接受并使用已经被语言科学界所普遍接受和推崇的科学方法。