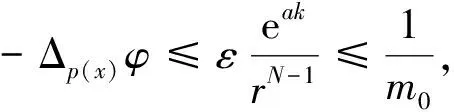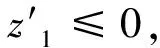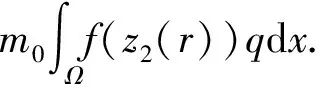基于上下解方法的p(x)-Kirchhoff型方程正解的存在性
2022-03-24容梅,缪清
容 梅, 缪 清
(云南民族大学 数学与计算机科学学院, 云南 昆明 650500)
0 引言
近年来,学者们采取多种方法对Kirchhoff型方程进行研究.如:Fan X L[1]对Dirichlet问题做出讨论,对于非变分问题,通过利用s+映射理论说明p(x)-Laplacian方程至少有一个解,并且利用山路引理证明变分问题有一系列解; Massar M等人[2和Cheng B T等人[3利用三临界定理解决了带有非局部的不同边界的多解问题; Fan X L[1]和Wang W H[4]利用山路引理和变分方法等来证明方程在定义域内有一系列的解.还有文献在处理非局部问题时,则是通过上下解方法得到Kirchhoff型方程或方程组至少存在一个正解[5-11].
上下解方法除了可以处理上述Kirchhoff型问题,还可以解决其他类型方程解的存在问题. 上下解方法不但能给出解的性质,而且对于非齐次项f,允许其有更为复杂的增长条件[12-13].
本文在前面文章的基础上,利用上下解方法研究了p(x)-Kirchhoff型方程

(1)
的正解存在性.其中Ω是N(N≥1)中具有光滑边界的有界区域,,),Mi(i=1,2)是连续函数并且满足条件:
(M0)Mi:[0,+∞)→[m0,+∞)连续单调递增函数,m0>1.
算子-Δp(x)(u)=-div(|u|p(x)-2u)称为p(x)-Laplacian算子,当p(x)=p(p为常数)时,该算子为p-Laplacian算子.方程(1)中的p(x)-Laplacian算子相比较p-Laplacian算子更为复杂:p-Laplacian算子满足(p-1)-齐次性,而p(x)-Laplacian算子是非齐次的.
本文研究的问题带有非局部项,使得方程不再是一个逐点的恒等式,这一类问题常被称为Kirchhoff型问题或者非局部问题,数学模型来自Kirchhoff方程
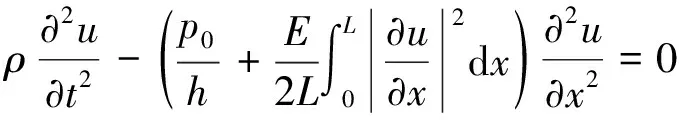
(2)
此类问题在实际应用中不断增多,研究较多的模型之一是电流变液的运动模型,其特点是在外部电磁波的影响下能够急剧改变机械性能[14].同时变指数增长条件的问题也出现在电流变流体的运动、非牛顿流体的流变学以及利用正压过滤等数学建模中[15-16].
定理1 若p(x)∈C1(N)满足(H1),Ω满足(H2),f和g∈C1满足(H3)、(H4),Mi(t)满足(M0),则方程(1)至少存在一个正解.
(H1)p(x)是径向对称,即p(x)=p(|x|),且sup|p(x)|<∞;
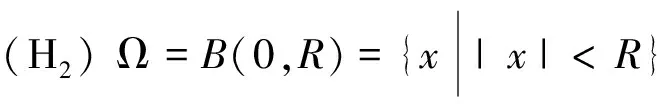
(H3)f,g:[0,+∞)→,且f,g为单调递增函数,满足

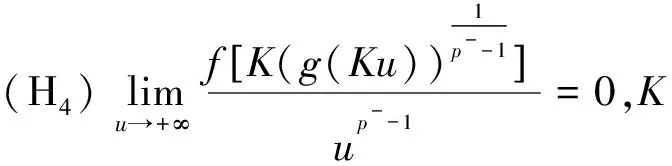
1 预备知识
定义
和W1,p(x)(Ω)空间
W1,p(x)(Ω)={u∈Lp(x)(Ω):Dαu∈Lp(x)(Ω),|α|≤1},
W1,p(x)(Ω)空间中的范数满足
‖u‖=|u|p(x)+|u|p(x),∀u∈W1,p(x).


(3)
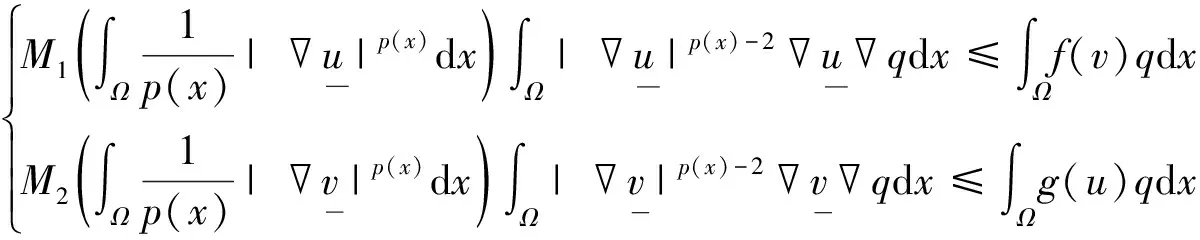
(4)


(5)
下面,将给出比较原则.
定理2[10]u,v∈W1,p(x)(Ω),并且满足(M0),若有下列不等式成立
其中(u-v)+=max{u-v,0},则u≤v(u,v∈Ω).
证明见文[11].
2 定理1的证明
接下来,将构造出下解(φ1,φ2)和上解(z1,z2),φ1≤z1,φ2≤z2,说明(φ1,φ2),(z1,z2)分别满足定义2中的不等式组,其中∀q∈W01,p(x)(Ω),q≥0,则方程(1)有一个正解.
步骤1 构造方程(1)的一个下解.
定义
则
通过计算可知φ≥0,由于φ′≤0,所以φ(r)是单调递减函数.而φ∈C1([0,R]),所以φ(x)=φ(|x|).
令r=|x|,根据
得到
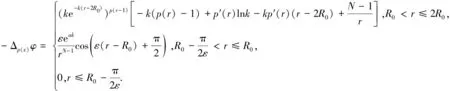
接下来,将在这三个区间中分别讨论M1Δp(x)φ与f(φ)的大小关系
首先,讨论当r∈(R0,2R0]的情况.因为φ(x)≥0,f是单调递增函数,所以f(φ(x))≥f(0).当k足够大时,-Δp(x)φ≤-ka 所以 由(M0)知M1≥m0,所以 -M1Δp(x)φ≤-m0Δp(x)φ 所以 -M1Δp(x)φ≤-m0Δp(x)φ≤1≤f(eak-1)≤f(φ),则-M1Δp(x)φ≤f(φ(x)). -m0Δp(x)φ=0≤1≤f(φ). 因此可得,当φ(x)∈C1(Ω)时,总有-M1Δp(x)φ≤f(φ(x)). 类似地,可以证明-M2Δp(x)φ≤g(φ(x)),所以(φ1,φ2)=(φ,φ)是方程(1)的一个下解. 步骤2 说明(z1,z2)是方程(1)的一个上解. 设z1为方程 的径向对称解,即z1=z1(r)=z1(|x|),且z1满足 所以 讨论 说明(z1,z2)是方程(1)的一个上解. 因为Mi≥m0>1,所以 由(H4)知 则当μ充分大时有 类似可得 可得 所以 由以上证明可知(z1,z2)是方程(1)的一个上解.由于μ充分大,且根据φ的定义可知φ1≤z1,φ2≤z2,所以方程(1)有一个正解.