蛛网图的邻和可区别染色
2022-03-24强会英谭钧铭
刘 欢, 强会英, 谭钧铭
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
图的染色问题是图论中最古老的问题之一,在现实生活中有着广泛应用.2013年,Flandrin等人首次提出图的邻和可区别染色的概念,并给出了一些特殊图的邻和可区别边色数[1].随后,Pilsniak等人给出了邻和可区别全染色的定义[2],得到了完全图、圈、二部图等图的邻和可区别全色数.蛛网图是一个重要的网络拓扑结构,对于网络权的分配和通信网络的设计有重要的指导作用[3].2014年,张东翰研究了蛛网图的邻强边染色,得到了其邻强边色数[4].2018年,李永艳讨论了蛛网图的邻点可区别V-全染色,得到其邻点可区别V-全色数[5].
受上述研究启发,本文讨论了蛛网图的邻和可区别边染色与全染色问题,得到了蛛网图的邻和可区别边色数和全色数.文中涉及的图均是有限、无向的简单图,记号V(G)、E(G)、Δ(G)、GΔ分别表示图G的顶点集、边集、最大度和全体最大度顶点在图G中的导出子图.符号{x1,x2,…,xn}→{a1,a2,…,an}表示用颜色序列a1,a2,…,an去染元素序列x1,x2,…,xn,其他未加说明的术语C5、[k]、C(x)、S(u),见相关文献[6-8].
1 预备知识
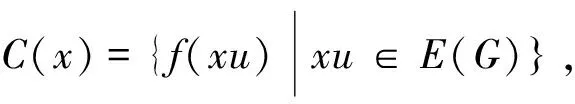
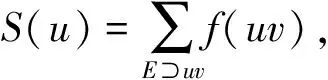
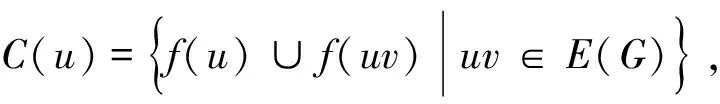
猜想1[2]若图G是阶至少为3的简单连通图,且G≠C5,则ndi∑(G)≤Δ(G)+2.

定义4[3]蛛形图Sk的头点为v0,从v0出发有k(k≥3)条路,除v0外,每条路有k个点,共有n(n=k2+1)个点,删去v0后,这k条路分别记为pi=vi1vi2…vik(1≤i≤k),eij表示pi中连接vi(j-1)和vij(1≤i≤k,2≤j≤k)的边,连接v0和vi1的边记为ei1(1≤i≤k).
定义5[4]设有蛛形图Sk,在Sk中添加边v1jv2j,v2jv3j,v3jv4j,v4jv5j,…,v(k-1)jvkj,vkjv1j(1≤j≤k-1)而得到的图称为蛛网图,记为wk.
引理1[8]对于简单图G,ndi∑(G)≥χ'a(G)≥Δ(G).若图G有相邻最大度点,则ndi∑(G)≥Δ(G)+1.

2 主要结论

证明1) 当k=3时,因为GΔ≠Ø,根据引理1知,ndi∑(G)≥Δ(G)+1=5.下面,给出图W3的一个5-邻和可区别边染色
{v0v11,v0v21,v0v31}→{1,3,5};{v11v21,v21v31,v31v11}→{4,2,3};
{v11v12,v21v22,v31v32}→{2,5,1};{v12v22,v22v32,v32v12}→{3,4,5};
{v12v13,v22v23,v32v33}→{4,1,2}.
按上述染法各点色集合与色数和,如表1所示.

表1 图W3各点色集合C(vij)和色数和s(vij)的情况
C(v11)表示与v11点相连的各边色集合,s(v11)表示v11点的色数和.(下表同)
从表1易见f是图W3的5-邻和可区别边染色.
2) 当k=4时,因为GΔ≠Ø,根据引理1知,ndi∑(G)≥Δ(G)+1=5.下面,给出图W4的一个5-邻和可区别边染色f:
f(v0vi1)=i,(1≤i≤4);f(vi1vi+1,1)=(i+2)(mod 4),(1≤i≤4);f(vi1vi2)=5,(1≤i≤4);
其余边按如下序列染法
{v12v22,v22v32,v32v42,v42v12}→{4,3,2,3};
{v12v13,v22v23,v23v33,v42v43}→{2,1,4,1};
{v13v23,v23v33,v33v43,v43v13}→{3,2,5,4};
{v13v14,v23v24,v33v34,v43v44}→{1,5,1,3}.
按上述染法有C(v0)={1,2,3,4},s(v0)=10.其余各点情况,如表2所示.

表2 图W4各点色集合C(vij)和色数和s(vij)的情况
由表2易得f是图W4的5-邻和可区别边染色.
3) 当k≥5时,因为GΔ=Ø,根据引理1知,ndi∑(G)≥Δ(G)=k.下面给出图Wk的一个k-邻和可区别边染色f,分成以下两种情况讨论:
情况1 当k≡1(mod 2)时,
①i≡1(mod 2),令f(v0vi1)=i,(1≤i≤k),
②i≡0(mod 2),令f(v0vi1)=i,(1≤i≤k),
当k≡1(mod 2)时,C(v0)={1,2,3,4,…,k};C(vik)={i-2};
C(vij)={(i+2(j-1))(modk),(i+2(j-1)+4)(modk),
(i+2(j-1)+2)(modk),(i+2(j-1)+3)(modk)},1≤i≤k, 1≤j≤k-1.
得到
情况2 当k≡0(mod 2)时,
①i≡1(mod 2),
②i≡0(mod 2),
f(vijv(i+1)j)=f(vi(j+1)vi(j+2)),(1≤i≤k-1,1≤j≤k-2);
f(vkjv1j)=f(vk(j+1)vk(j+2)),(1≤j≤k-2);
f(vi(k-1)v(i+1)(k-1))=f(v0vi1),(1≤i≤k-1);f(vk(k-1)v1(k-1))=f(v0vk1).
当k≡0(mod 2)时,
C(v0)={1,2,3,4,…,k};
C(vij)={(i+2(j-1)+1)(modk),(i+2(j-1)+5)(modk),(i+2(j-1)+3)(modk),
得到
s(vik)=i-1,(1≤i≤k).
综上所述,此定理成立.经验证,蛛网图的邻和可区别边染色符合猜想1.
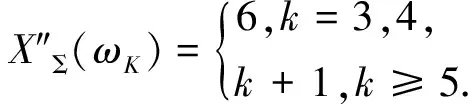
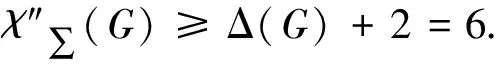
f(vijvi(j+1))=(i+j+2)(mod 6),(1≤i≤3, 0≤j≤3 );
{v11v21,v21v31,v31v11}→{6,2,1};
{v12v22,v22v32,v32v12}→{1,3,2};
f(v0)=1;f(vij)=i+j,(1≤i≤3, 1≤j≤3 ).
按上述染法各点色集合与色数和,如表3所示.

表3 图W3各点色集合C(vij)和色数和c(vij)的情况
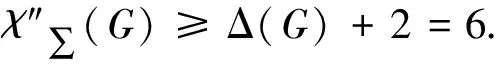
f(vijvi(j+1))=(i+j+2)(mod 6),(1≤i≤4,0≤j≤4);
f(vijv(i+1)j)=i+j-1,(1≤i≤3,1≤j≤3);
f(vkjv1j)=1+j,(1≤j≤3).f(v0)=1;
f(vij)=(i+j)(mod 6),(2≤i≤4, 1≤j≤4 );
{v11,v12,v13,v14}→{6,1,2,5}.
此时,C(v0)={1,3,4,5,6},c(v0)=21.其余各点情况如下表所示.
由表4可,f是图W4的6-邻和可区别全染色.

表4 图W4各点色集合C(vij)和色数和c(vij)的情况
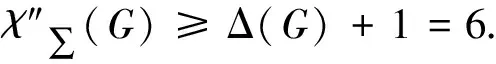
f(v0)=6;f(vij)=(i+2j-1)(mod 6),(1≤i≤4,1≤j≤5);{v24,v45}→{6,4};
{v51,v52,v53,v54,v55}→{3,2,4,6,1}.f(v0vi1)=i,(1≤i≤5);
其余边按如下序列染法,
{v11v21,v21v31,v31v41,v41v51,v51v11}→{5,6,1,2,4};
{v12v22,v22v32,v32v42,v42v52,v52v12}→{1,2,3,4,3};
{v11v12,v21v22,v31v32,v41v42,v51v52}→{6,4,5,6,1};
{v13v23,v23v33,v33v43,v43v53,v53v13}→{3,4,6,1,2};
{v12v13,v22v23,v32v33,v42v43,v52v53}→{5,6,1,5,6};
{v13v14,v23v24,v33v34,v43v44,v53v54}→{1,5,3,2,5};
{v14v15,v24v25,v34v35,v44v45,v54v55}→{5,1,5,1,2};
{v14v24,v24v34,v34v44,v44v54,v54v14}→{4,2,6,4,3}.
按上述染法有C(v0)={1,2,3,4,5,6},c(v0)=21.其余各点情况,如表5和表6所示.

表5 图W5各点C(vij)的情况
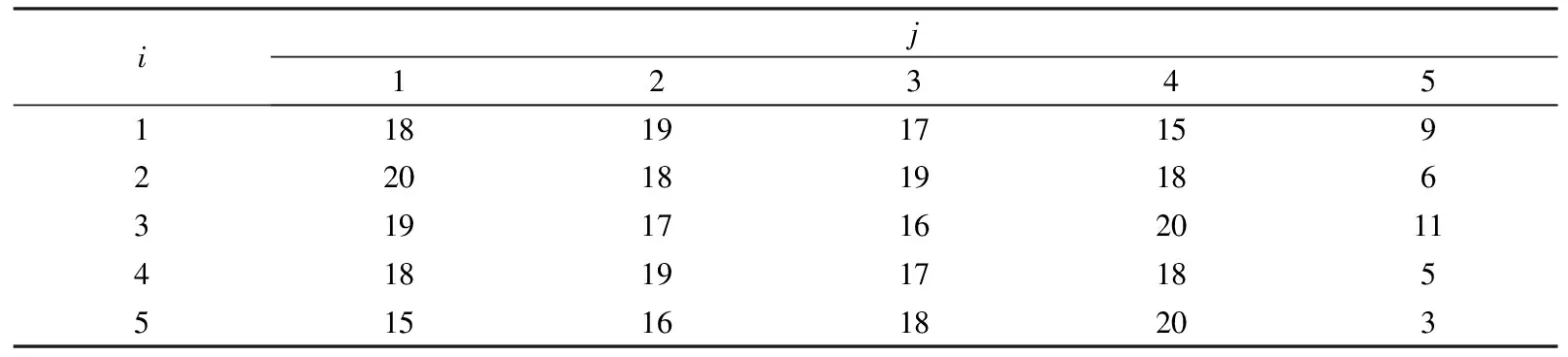
表6 图W5各点c(vij)的情况
由表6易见,f是图W5的6-邻和可区别全染色.

对于图G中的邻和可区别边染色,规律同定理1.对于图G的点染色
f(v0)=k+1;f(vij)=(f(vi(j-1)vij)+1)(modk),(1≤i≤k, 1≤j≤k).
按上述染法得色集合及色数和,如下所示.
① 当k≡0(mod 2)时,C(v0)={1,2,3,…,k,k+1};
C(vij)={(i+2(j-1)+1)(modk),(i+2(j-1)+5)(modk),(i+2(j-1)+3)(modk),
C(vik)={i-1,i},(1≤i≤k).
得到
② 当k≡1(mod 2)时,C(v0)={1,2,3,…,k,k+1};C(vij)={(i+2(j-1))(modk),
(i+2(j-1)+4)(modk),(i+2(j-1)+2)(modk),(i+2(j-1)+3)(modk),
(i+2(j-1)+1)(modk)},(1≤i≤k,1≤j≤k-1);C(vik)={i-2,i-1}.
得到
综上所述,f是图Wk的一个k+1-邻和可区别全染色.经验证,蛛网图的邻和可区别全染色符合猜想2.由此可见,蛛网图的邻和可区别染色满足图的邻和可区别边染色和全染色猜想.
