基于SCA-LSSVM的电涡流传感器温度补偿方法研究*

李玉军王琛琛焦尚彬张 青.王 庆

(1.西安理工大学自动化与信息工程学院，陕西 西安 710048；2.陕西省复杂系统控制与智能信息处理重点实验室，陕西 西安 710048；3.西安理工大学晶体生成设备及系统集成国家地方联合工程研究中心，陕西 西安 710048)

电涡流传感器被广泛应用于电力、石油、化工、冶金等行业和一些科研单位，其可长期可靠工作、灵敏度高、抗干扰能力强、非接触测量、响应速度度快、不受油水等介质的影响，并在大型旋转机械的轴位移、轴振动、轴转速等参数进行长期实时监测中被广泛应用[1]。但在实际应用中发现，电涡流传感器的输出易受到外界环境温度影响，产生温度漂移现象，从而直接影响传感器的稳定性和系统的检测精度。因此，需建立温度补偿模型对电涡流传感器进行校正，减少环境温度对传感器输出精度的影响[2－3]。

传感器温度补偿的方式有软件补偿和硬件补偿两种方式。硬件补偿需要设计复杂的硬件电路来减少误差，消除温度漂移现象，但是一旦环境温度发生变化，硬件电路的参数不能及时的完成补偿校正，导致传感器输出精度得不到保障。目前采用比较多的方式是软件补偿[4]，相对于硬件补偿方式来说，软件补偿手段比较简单，且实现起来比较容易。软件补偿往往采用信息融合技术来减少干扰量对传感器测量精度的影响，软件补偿的手段有很多，比如支持向量机、神经网络等等，而神经网络模型的输出差异性比较明显，每次输出预测不一致且容易陷入局部最优，最终神经网络预测的精度和收敛性是否良好和初始权值的选取有很大关系，导致很难建立最佳的网络模型[5－6]。

针对神经网络模型的弊端，考虑到支持向量机(SVM)在用于回归估计时有较好的泛化能力，对于非线性样本数据回归效果较优，可以有效解决电涡流传感器输出准确度较低这一问题，因此非常适用于电涡流传感器的温度补偿[7]。此外，针对支持向量机在建模过程中惩罚因子和核函数参数选取比较困难这一问题，可以通过智能优化算法在有效迭代范围内进行全局搜索，因此来获得更佳的参数[8]。同时，为了提高非线性信号的处理准确度和精度，往往采用最小二乘支持向量机作为建模方法，在传感器温度补偿方面有着良好的应用[4，9－13]，且在文献中通过实验验证了采用PSO算法优化LSSVM进行传感器温度补偿效果优于已有的温度补偿方法[10－12]。

针对电涡流传感器的温度漂移问题，在传感器不同标定位移下，通过改变环境温度，采集了多组传感器输出电压值。建立了最小二乘支持向量机传感器回归模型，通过正余弦优化算法和粒子群优化算法分别对最小二乘支持向量机的参数进行优化，得出最佳的传感器回归模型优化选取参数。通过实验发现，SCA-LSSVM在算法优化效率和模型预测精度上均优于PSO-LSSVM，可以作为传感器温度补偿模型用于实际工程之中。

1 正余弦(SCA)优化算法简介

澳大利亚学者Mirjalili在2016年提出了正弦余弦算法(SCA)，它是一种新时代下的智能优化算法，已经逐渐被国内外大部分学者研究和优化[13－15]。和以前很多智能优化算法不同，以往的智能优化算法往往采用仿生的思想，而SCA优化算法则利用了数学函数思想。正余弦优化算法采用了创新思路，以正余弦函数波动性、周期性特征为出发点进行构思，通过创建多个随机候选解构建正余弦数学模型来求解优化问题。正余弦算法不仅本身比较简单且容易实现，而且其参数很少且具有很快的收敛速度[14－15]。

正余弦算法总体思路比较简单，先随机初始化种群X，种群X由m1，m2，m3，…，m N个个体组成，对于具体个体来说，它有包含了n1，n2，n3，…，n N个维度，再用适应度函数选出当前所有个体中最好的个体，记为gbest，最后在迭代的过程中不断更新个体位置，具体如式(1)所示:

式中:d表示当前迭代次数，其中a为一个常数，通常设置为2，D表示最大迭代次数。在正余弦优化算法迭代寻优时r1，r2，r3，r4这几个参数具有不同的作用。下一次迭代的时候个体位置的具体方向由r1决定，它在正余弦优算法的开发以及探索阶段起到了平衡作用，其中开发和算法的局部开发能力对应，探 索和算法的全局寻优能力对应。式(1)中，若r1sin(r2)或者r1cos(r2)的值在(－∞，－1)∪(1，＋∞)之间时，此时正余弦算法在全局探索阶段，若r1sin(r2)或者r1cos(r2)的值在(－1，1)之间时，此时正余弦算法正在局部开发；下一次迭代的时候个体位置移动距离由r2决定；下一次迭代的最优个体确定由随机权重r3决定；由于r4∈[0，1]，它可以保证正余弦优化算法以相同概率的形式在正余弦部分迭代并且更新个体位置。

2 温度补偿建模与实验分析

2.1 SCA-LSSVM温度补偿模型

电涡流传感器静态标定后的输入输出关系为U S＝f(S)，当加入环境温度影响参数T之后，输入输出函数关系为:U S＝f(S，T)，为了实现温度补偿采用逆模型思想，即确定温度补偿模型为涡流传感器输出位移S关于电涡流传感器输出电压U S和环境温度传感器输出电压U T的二元函数如式(3)所示:

式中:U S1，U S2，U S3，…，U Sn为电涡流传感器输出电压值，U T1，U T2，U T3，…，U Tn为温度传感器输出电压值，S1，S2，S3，…，S n为电涡流传感器标定位移量。

建立最小二乘支持向量机(LS-SVM)传感器回归模型，用正余弦优化算法(SCA)对LS-SVM模型中的参数进行寻优，将实验标定得到的实验数据输入到模型中，最终得到经过温度补偿后的计算结果，模型框图如图1所示。

图1 温度补偿模型框图

由图1可以看出，涡流传感器输出电压U和环境温度T为温度补偿模型的输入，位移S为模型输出，SCA-LSSVM和PSO-LSSVM通过对训练样本学习，会建立电涡流传感器输出电压U s、环境温度传感器输出电压U T和标定位移S之间的逼近函数关系，通过模型补偿后使得模型计算结果S和标定位移S之间的误差达到最小，则传感器输出位移更加接近标定位移，从而达到补偿效果。

2.2 温度补偿实验及实验分析

温度补偿实验装置选择上海一恒圣科仪器公司生产的型号为DZF－6050的真空恒温箱。将电涡流传感器与被测铝板及温度传感器DS18B20固定在标定台上并且整体置于恒温箱中，温度传感器DS18B20检测涡流传感器周围环境温度，DS18B20测量温度范围为－55℃～＋125℃，完全满足测量要求。电涡流传感器和DS18B20在23℃～60℃温度变化范围内采集了22组随温度变化的样本数据，每组数据是在标定位移值不变的情况下，随着恒温箱温度增高，记录此时的温度传感器实时温度以及电涡流传感器的输出电压值，待一组数据测试完之后，增大位移量，开始下一组实验，位移变化范围为2.5 mm～13 mm之间，整个实验一直循环进行下去。最终将23℃～60℃下的涡流传感器输出电压值和温度传感器实时温度存储下来，并且通过串口实时读取样本数据到上位机，共记录了7 522个样本数据，部分实验数据如表1所示。

表1 温度补偿部分实验数据

由表1数据可以看出，在同一标定位移条件下，涡流传感器的输出电压也会随着温度的升高而升高。由此可见环境温度对于涡流传感器的输出的影响巨大。为了直观的看出传感器受温度影响产生温度漂移的现象，待温度补偿实验完成之后，将同一标定位移下，不同温度对应的传感器输出电压值进行分析。

如图2所示，横坐标为不同标定位移下的温度值，纵坐标为不同温度下电涡流传感器输出电压值，可以发现电压输出一直增大，且具有严重的非线性漂移。

图2 温度漂移仿真结果图

由表1实验数据可得:在满量程条件下，涡流传感器的最大输出电压值UFS＝2.535 V，当温度的变化范围为ΔT＝37℃(由23℃至60℃)，满量程输出值由2.535 V下降到2.473 V，输出变化范围ΔU＝0.062 V。

由此可得到模型校正前电涡流传感器的温度灵敏度系数如式(4)所示:

2.3 温度补偿模型结果分析

本文采用正余弦优化算法对最小二乘支持向量机的惩罚因子c、核函数参数δ进行优化，提高最小二乘支持向量机的收敛速度，最小二乘支持向量机的适应度函数由均方误差进行表征，均方误差如式(5)所示:

式中:S j为第j个样本标定值，S′j为第j个样本预测值，n为样本总数。

LS-SVM算法中的惩罚因子c和核函数参数σ往往需要合理选择，σ的选择范围在0～20之间，c的选择范围一般在0～100 000之间，算法执行过程如下:

Step 1 将温度补偿实验测得的7 522组数据间隔取一半样本，即3 761组样本作为训练样本输入，标定位移作为训练样本输出，对样本数据归一化，测试样本选择全部数据。

Step 2 对正余弦算法的参数进行初始化，将群体数目N设为10，对种群X i，j进行随机初始化，i取值范围1～10，对应种群中十个个体，j取值1－2，分别对应待优化的惩罚因子c和核函数参数σ；最大迭代次数为100；

Step 3 将初始化得到的十组待优化的参数组合(c，σ)，即种群X i，j代入校正模型进行计算，通过适应度函数式(5)，可以得到十组适应度函数值，从而可以得到当前最优参数组合gbest。

Step 4 将式(2)中的α设为2，通过当前迭代次数、最大迭代次数和α求出r1，通过rand函数随机产生r2，r3，r4。根据式(1)计算得到下一代参数组合(c，σ)，即新一代种群X i，j。

Step 5 进行算法终止条件检查，如果未能找到最优解则重复Step 3～4，否则输出最优解。

算法优化过程如图3所示。

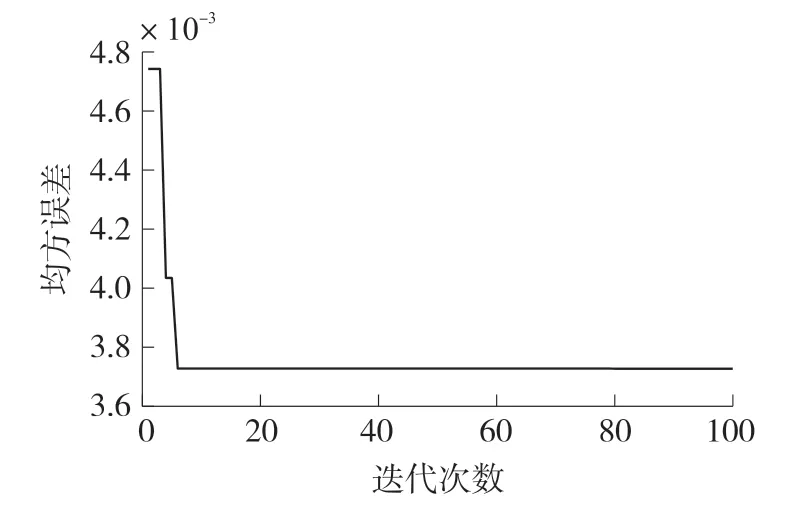
图3 SCA-LSSVM算法优化过程

图3中，横轴为迭代次数，纵轴为模型预测结果均方误差。在100次优化迭代次数下，SCA-LMSVM算法在10代左右已经收敛，模型计算结果均方误差为9.97×10－4。模型输出结果如图4所示。

图4 SCA-LSSVM算法预测结果

图4中，X轴样本编号，Y轴位移值。SCALSSVM温度补偿后计算结果和标定值之间的误差较小，两条曲线融合度较好。得到惩罚因子c为21 711.81，核函数参数σ为0.033 6。

采用PSO算法对LS-SVM模型参数寻优，LSSVM算法的核函数同样选择映射关系为非线性的高斯核函数。根据PSO-LSSVM算法可以得到优化过程如图5所示。

图5中，X轴为迭代次数，Y轴为模型预测结果均方误差。由图中可以看出在40代左右算法收敛即达到全局最优解，模型计算结果均方误差为4.39×10－3。

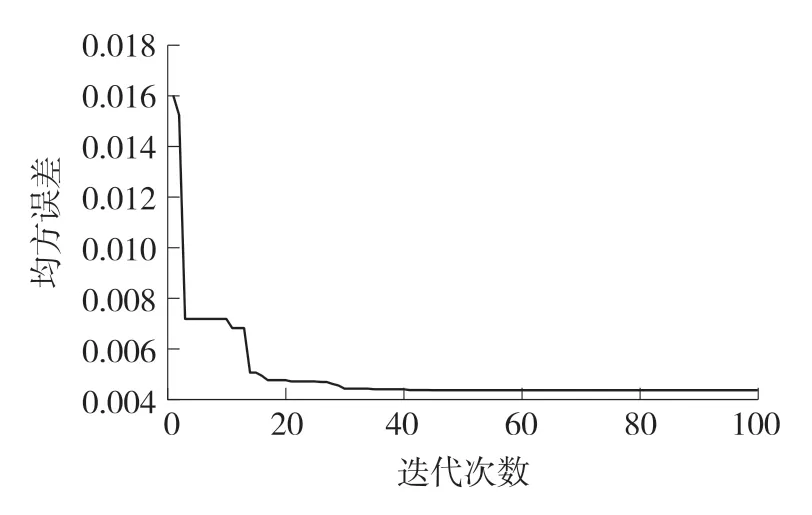
图5 PSO-LSSVM算法优化过程

PSO-LSSVM模型计算结果如图6所示。图6中，X轴为样本编号，Y轴为位移值。PSO-LSSVM算法优化得到惩罚因子c为2 713.71，核函数参数σ为0.031 8。

图6 PSO-LSSVM算法预测结果

将优化得到的参数(c，σ)代入回归模型可以得到参数优化之后的系统模型参数。根据系统模型参数可以得到实测模型，将其移植到单片机中即可用于实际测量。

3 模型校正效果对比分析

根据式(4)可以得出电涡流传感器温度补偿前的温度灵敏度系数为6.61×10－4/℃。由表2测试样本数据看出，经过PSO优化的最小二乘支持向量机涡流传感器回归模型预测结果在温度的变化范围为ΔT＝37℃内(由23℃至60℃)，满量程位移ΔS＝13 mm，模型计算值最大偏差量｜ΔS′m｜＝｜13.006 4－12.969 7｜＝0.036 7 mm，得到PSO-LSSVM模型优化校正后电涡流传感器的温度灵敏度系数如式(6)所示:

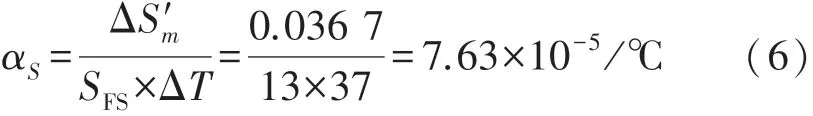
根据表2的数据，经过SCA优化的最小二乘支持向量机涡流传感器回归模型预测结果在温度的变化范围为ΔT＝37℃内(23℃至60℃)，满量程位移ΔS＝13 mm，｜ΔS′m｜＝｜13.003 4－12.999 2｜＝0.004 2 mm，从而可以得到SCA-LSSVM模型优化校正后涡流传感器的温度灵敏度系数如式(7)所示:

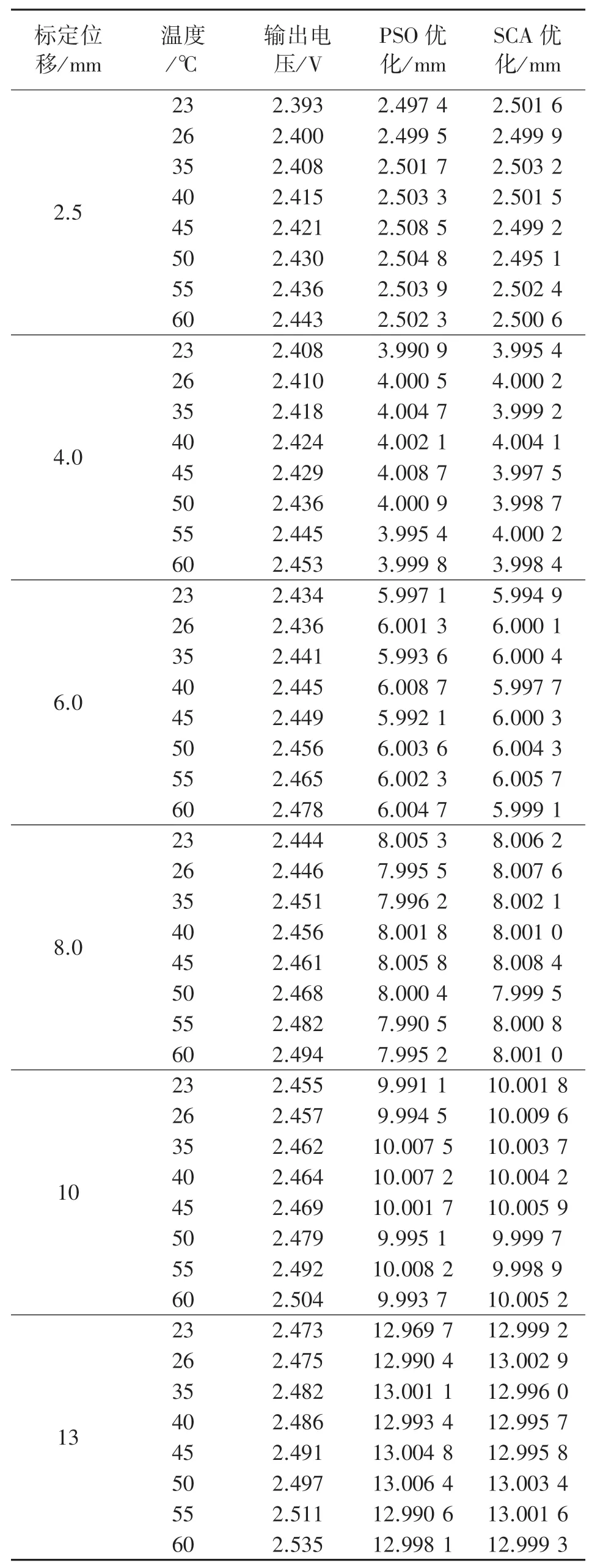
表2 电涡流传感器温度补偿后部分数据

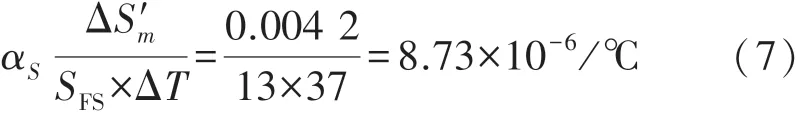
SCA和PSO算法优化后的传感器温度补偿参数评估结果如表3所示。

表3 算法优化后参数评估结果对比

从表3可以看出，经过PSO优化后的最小二乘支持向量机涡流传感器回归模型的温度灵敏度系数为7.63×10－5/℃，比补偿前提高了一个数量级，说明经过粒子群优化后的最小二乘支持向量机传感器回归模型的温度稳定性提高了不少。而经过正余弦优化后的模型在各项评价参数方面都比粒子群有很大提升，温度灵敏度系数为8.73×10－6/℃。比补偿前提高了两个数量级。综上，说明了正余弦优化后的传感器回归模型温度稳定性大大提高，传感器工作时受温度影响较大的弊端得到了很好的抑制，有效降低了温度漂移现象，提高了传感器测量精度。

4 结论

本文针对电涡流传感器受环境温度影响产生温度漂移这一实际问题，通过对最小二乘支持向量机传感器回归模型的惩罚因子和核函数参数进行优化选取，提出了正余弦算法优化最小二乘支持向量机的温度补偿模型，并且和PSO-LSSVM进行对比。结果表明，SCA优化后模型计算结果均方误差为9.97×10－4，算法优化耗时578 s，模型校正后的传感器的温度灵敏度系数为8.73×10－6/℃。PSO优化后模型计算结果均方误差为4.39×10－3，算法优化耗时782 s，模型校正后的传感器温度灵敏度系数为7.63×10－5/℃。实验结果表明，经过SCA优化后的传感器回归模型温度灵敏度系数比补偿前降低两个数量级，PSO优化后仅降低了一个数量级。此外，SCA算法优化时间比PSO减少很多，且预测准确度比PSO提升了一个数量级。综上，SCA算法优化效率和精度方面优于PSO算法，将优化得到的模型参数代入LS-SVM可以得到实测模型，将其移植到单片机中即可用于实际测量，从而提高了传感器的稳定性，对于电涡流传感器实际应用具有非常重要的意义。