基于ABAQUS的角接触球轴承动力学仿真分析

2022-03-24陈明东冯育龙麻爱松

机械与电子 2022年3期

陈明东，许涛,2，冯育龙，吕欢，麻爱松

(1.西安工程大学机电工程学院，陕西西安 710600；2.西安市现代智能纺织装备重点实验室，陕西西安 710600)

0 引言

轴承作为平模枪钻核心部件，其性能将直接影响平模枪钻回转精度和使用寿命。轴承在高转速、周期性交变的载荷作用下，将产生大量摩擦热，使轴承温度升高，随温度升高轴承位移也将发生变化，严重时将引起轴承过早失效，设备发生故障。因此，分析轴承不同转速下温升和位移是控制轴承动态性能、提高设备使用寿命的关键。

现阶段，热网络法和有限元法是角接触球轴承数值仿真中常见的分析方法[1]。热网络法将研究对象划分为多个单元节点，根据Harris理论以及Kirchhoff理论建立传热模型，迭代求解轴承转速和接触载荷等参数，得到轴承各部件温度和位移[2]。李振峰等[3]用热网络法建立轴承稳态温度计算模型，求解不同转速、载荷和润滑油温度下轴承温度及整体生热量；Zheng等[4-5]通过建立新型多节点热网络模型，分析高速角接触球轴承负载、径向和轴向传热；Yan等[6]基于热结构相互作用建立轴承瞬态热网络模型，比较整体方法和局部方法计算轴承产热。有限元法是将有限元模型离散为单元组合体，单元之间通过节点连接起来，通过对每一个单元求近似解从而得到整个求解域上场函数的近似值[7]。Wang等[8]建立轴承和主轴系统瞬态热分析有限元模型，并将其与边界条件相结合，实时估算轴承的热特性；Ye等[9]通过建立高速角接触球轴承有限元模型进行热分析，并根据轴承径向热膨胀对几何参数进行优化，对轴承特性和疲劳寿命进行分析；Ma等[10]综合考虑边界条件等影响因素，建立高速主轴系统热特性分析有限元模型，求解出主轴热位移。

热网络法求解精度受节点数量限制，且轴承在高速运行状态下工况极其复杂，热产生和热传导受多种因素影响，难以获得轴承内部温度分布。尽管许多学者对经验公式中的系数进行修正，但使温度计算结论趋近于实验结果依旧十分困难。有限元法已经广泛应用于轴承非线性数值分析，当前学者未充分综合考虑轴摩擦产热过程和非线性边界条件等方面融合影响过程，使得仿真结果与实际情况差异较大。

针对上述问题，本文以平模枪钻角接触球轴承为研究对象，基于Palmgren摩擦生热理论，在ABAQUS中建立角接触球轴承完全热力耦合有限元模型，对轴承稳态温度场和轴向位移场做分析与计算，得到转速对轴承稳态温度场及位移的影响规律。

1 球轴承发热量计算

轴承发热主要产生于轴承滚珠与润滑剂间局部差动滑动而引起的摩擦、轴承在外部载荷作用下产生的摩擦以及轴承滚珠自旋引起的滑动摩擦。根据Palmgren和Harris经验公式，轴承产生的热量与摩擦力矩有关。

轴承滚珠与润滑剂间黏性摩擦力矩Mv计算式为

(1)

f0为与轴承类型及润滑方式相关的系数，对于脂润滑角接触球轴承f0=2；v为润滑剂粘度；n为角接触球轴承转速；dm为角接触球轴承节圆直径。

轴承在外部载荷作用下产生的摩擦力矩Ml计算式为

Ml=f1Fβdm

(2)

轴承滚珠自旋摩擦力矩Ms计算式为

(3)

μ为滚珠与内、外圈滚道间摩擦系数；F为滚珠与内、外圈滚道法向接触载荷；a为滚珠与内、外圈滚道接触椭圆长半轴；Σλ为滚珠与内、外圈滚道接触椭圆第二类完全积分。

由于轴承在转动过程中，不同位置滚珠与内、外圈滚道接触状态不同，导致受力不同，第j个滚珠与内、外圈滚道之间摩擦力矩Mij、Mej为：

(4)

(5)

Z为滚珠个数；Db为滚珠直径；de为轴承外圈滚道直径；di为轴承内圈滚道直径。

在角接触球轴承高速运转过程中，由于存在接触角，所以在轴承转动过程中，自旋运动始终存在。根据外滚道控制理论，与外圈滚道之间为纯滚动，自旋摩擦力矩可忽略。故第j个滚珠与内、外圈滚道接触产生的热量Hij、Hej为：

Hij=ωbMij+ωsiMsi

(6)

Hej=ωbMej

(7)

(8)

γ′=Db/dm；β为滚珠旋转轴在径向平面上投影与旋转轴在垂直平面内夹角；αs为轴承滚珠与内圈接触角。故该轴承在内、外圈滚道摩擦所产生的热量Hi、He为：

(9)

(10)

假设对于该轴承，轴承总发热量为内、外圈接触发热之和[11]，轴承内产生的热量主要通过热传导和热对流的方式传递。滚珠与轴承外圈滚道摩擦产生的热量He及滚珠与轴承内圈滚道产生的热量Hi传递如图1所示。

图1 热量传递

轴承中主要存在与润滑剂之间强制对流和与空气之间对流，根据Harris滚动轴承对流换热系数计算模型[12]，轴承与润滑剂间换热系数hl计算式为

(11)

kl为润滑剂的导热系数；Re为雷诺数；Pr为润滑剂的普朗特数。

轴承外表面与空气之间的对流换热系数hair为

(12)

T为轴承部件温度；Tair为环境温度；kair为空气导热系数；D为轴承外径。轴承座位置相对固定，轴承与其对流形式为自然对流，主轴以一定速度转动，轴承与其对流形式为强迫对流。

2 角接触球轴承有限元模型

2.1 有限元模型的建立

本文以某平模枪钻前轴承7906C角接触球轴承为例，利用ABAQUS建立轴承有限元模型对轴承运转过程的温度场和位移进行仿真分析。角接触球轴承7906C由内、外圈、滚珠和保持架4部分组成，结构参数如表1所示。

表1 角接触球轴承7906C的结构参数

在有限元仿真过程中，为提高求解效率，简化计算，方便网格划分，对模型采取以下简化设定。

a.轴承保持架主要功能为保持各滚珠之间相对位置，保证轴承正常运行，在有限元分析中，保持架不受外力作用。为简化模型，提高仿真效率，在有限元模型中使用MPC link连接轴承各滚珠，实现保持架在实际运转过程中的作用。

b.内、外圈上过渡圆角及倒角等特征主要作用为减小应力集中及方便安装，此类结构对有限元分析精度影响不大。为方便网格划分，提高网格质量，删去此类特征。

c.轴承滚动体与内、外圈之间的摩擦符合库伦定律，且摩擦系数、热膨胀系数等参数不随温度和应力的变化而变化。

d.忽略轴承中轴向游隙、径向游隙以及油膜的影响。

e.在划分轴承网格时，所有部件划分为六面体结构化网格，使其具有较高的计算精度和效率，并将轴承各部件的单元类型设定为Explicit，Coupled Temperature-Displacement。

根据以上条件建立的角接触球轴承有限元模型中共有73 272个线性六面体单元，92 164个节点。

角接触球轴承7906C中内外圈、滚珠的材料为GCr15轴承钢，其力学、热力学性能参数如表2所示。

表2 角接触球轴承7906C的材料参数

由于ABAQUS中未统一单位，为保证有限元模型中各物理量单位的一致性，在仿真前需要确定单位量纲，本文选用国际单位制中mm-t-s-K单位制。

2.2 边界条件及载荷设定

角接触球轴承动力学仿真分析为高度非线性问题，为使仿真结果更精确，需对模型边界条件和载荷采取以下设定。

a.轴承运转过程中，滚珠与内、外圈滚道相互接触，接触类型为面-面接触，将轴承内、外圈滚道定义为接触主面，滚珠表面为从面。

b.设置接触属性时将轴承切向摩擦定义为罚函数，摩擦系数为0.03；法向摩擦定义为硬接触，默认其约束执行方法[13]。假定摩擦副的机械能全部转化为热能，且均匀传入各接触面。

c.将轴承各部件和环境温度初始温度设置为20 ℃。

d.对轴承外圈施加ENCASTRE约束，并沿轴向方向加载350 N的载荷；轴承内圈释放其绕轴旋转方向自由度，固定其他方向自由度。由于轴承内圈为实体，无法直接施加转速，故在轴线上选取1点创建RP点与轴承内圈进行耦合，在该点上施加不同的转速，使得轴承内圈转动。

完成以上设定后提交分析作业，利用ABAQUS显式求解器Dynamic，Temp-disp，Explicit计算分析轴承温度场与位移变化。

3 仿真分析

本文所选取的平模枪钻最高转速可达15 000 r/min，在实际工况中，平模枪钻常用工作转速区间为5 000～12 000 r/min，故针对该区域转速对轴承工作状态进行仿真分析。

对角接触球轴承施加350 N轴向力，并对内圈加载10 000 r/min转速，得到轴承整体及各部件温度云图如图2～图5所示。由于分析步时间小于轴承整体达到热平衡时所需时长，仅在滚珠与内外圈接触区域存在热扩散现象。

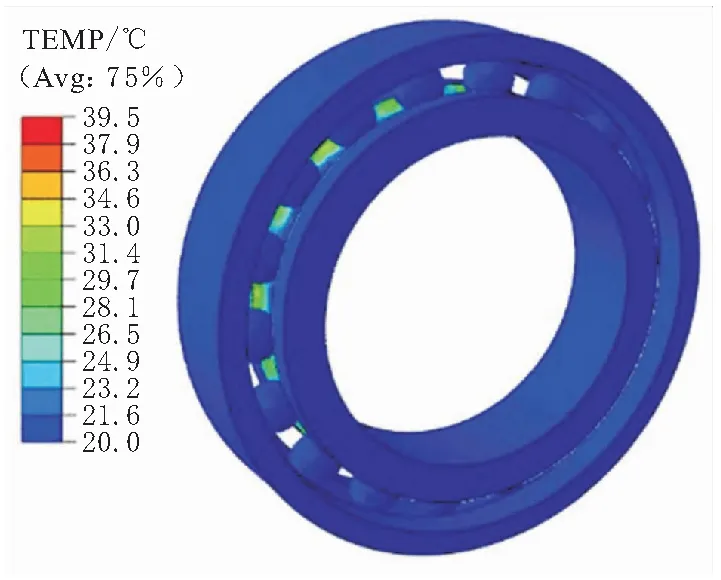
图2 轴承整体温度云图

图3 滚珠温度云图

图4 内圈温度云图

图5 外圈温度云图

由图2～图5可知，轴承内圈温度变化最大，温度最大值为39.5 ℃，其次为滚珠和外圈，且距离接触区域越远的部位，温度变化越小。为验证接触区域是否达到热平衡，将轴承接触区域初始温度场数值设置为39.5 ℃并增加分析步长再次提交作业进行仿真分析，仿真结果中，轴承各部件温升缓慢，达到稳态时，温度最大值为41.1 ℃，如图6所示。