基于改进MCMC的疫情人群管控模型
2022-03-23郑辰彦王露露胡益传
郑辰彦,王露露,胡益传
(华东交通大学 经济管理学院,南昌 330013)
近年来重大突发疫情在全球范围内频发,如2003年的“非典”(SARS)、2009年的美国大流感(H1N1)、2015年的中东呼吸综合征(MERS)、2018—2019年的埃博拉(Ebola)和当前全球蔓延的新冠肺炎(NCP),这些传染性极强、致死率极高的疫情频发说明人类与病毒的斗争将是长久的、持续的。2019年发生的新冠肺炎疫情因传播速度快、传播规律复杂、潜伏期长等特征迅速席卷全球,这必然给人民生命财产安全带来巨大的损失,各国政府管理部门面临艰难的挑战。世界各国由于社会文化、政府体制、政府能力各不相同,导致各国政府处理疫情的措施也不一样,取得的效果也不一样。中国在疫情暴发后,很快地控制了疫情的发展,从当前的效果来看,应该说是世界上疫情控制得最好的国家。美国和印度是采用市场管理的办法,现在看来是处理得最差的国家。韩国等结合其国情,采取了人群管制的措施,对感染者人群进行了隔离治疗,也取得了较好的成绩。此次新冠肺炎,是人类首次遇到的传染性强、致死率高的传染病。与其他传染病不同,新冠肺炎的传播规律复杂,除了存在易感者、潜伏者、感染者和康复者,甚至还存在大量的疑似患者,这些疑似者中就有一定的感染者,导致部分疑似者存在着传染性。另外,潜伏者也存在传染性。对于快速传播的高致病性传染病来说,信息获取的滞后所造成的后果是不可掌握的。因此,在不同的疫情管控策略下,找到符合新冠肺炎传播规律的传染病模型来预测疫情的发展趋势,进而能够及时发现、追踪和预测传染病的传播规律,为实行有效的公共卫生干预措施提供数据支撑。这在没有治疗的特效药与接种疫苗的情况下,具有十分重要的理论意义与现实指导意义。与本文相关的研究主要集中于传染病模型的建立、传染病模型的参数估计和传染病临界阈值的推导。
在传染病模型方面,Chen等研究了具有感染年龄和饱和发病率的SIR流行模型[1]。Cai等研究了具有比率依赖的传染病模型的全局动力学和相应的SIRS随机微分方程[2]。Wu等在2019-nCOV的疫情背景下建立了SEIR传播动力学模型[3]。每种疫情的发生发展总有一些特殊的情景,便有学者将经典SEIR模型根据实际情况进行改进,Liu等提出了一种具有年龄依赖性潜伏期和复发性疾病的SEIR流行模型[4]。Alonso-Quesada等研究了一类SEIR流行病模型的离散化与控制问题[5]。赵英英等考虑标准发生率和信息干预因素,建立了SIRS传染病模型[6]。王改霞等构建了 SIQRS型传播模型来分析无病平衡点的局部稳定性以及接种最优策略[7]。梅珊等考虑个人行为、交通信息和地理信息因素建立了空气传播动力学模型[8]。李勇建等建立了Petri网传染病传播模型[9]。
在传染病模型的参数估计方面,George等以模型拟合值和实际传染病数据之间的随机误差平方和最小化原则,估计出传染病模型的相关参数[10]。Aranda等建立了寨卡病毒感染者进化的数学模型,使用哥伦比亚2016年寨卡流行的真实数据对传播动力学模型进行参数估计[11]。Li等提出了一种基于遗传算法的参数估计方法来估计埃博拉病毒模型的参数[12]。Korolev通过几种非线性SUR估计出流行病学模型的参数[13]。Kim等建立了SEIQR传染病模型预测韩国疫情发展,通过最小二乘法估计模型的参数[14]。李倩等基于新型冠状病毒疫情背景,建立了SEIR型疫情传播动力学模型,使用了最小二乘法对模型参数进行了估计[15]。崔景安等通过实时疫情数据对模型参数进行估计[16]。郭尊光等建立了SEIR反应扩散传染病模型,并用最小二乘优化方法对模型中的传染率参数进行估计[17]。
基本再生数是传染病领域的一个重要阈值参数,用来衡量传染病的传播能力和发展趋势。一般在传染病发展初期,基本再生数是一个常数,随着管控措施的实施,基本再生数动态变化,这时候称之为有效再生数。在传染病的临界阈值方面,Lim等针对特定肠道病毒类型,依据疫情暴发的最初生长阶段累积报告的病例数,来估计基本再生数的具体数值[18]。Kucharski等通过统计随机模拟的方法预测病例数,根据病例数落入区间的比例来估计基本再生数[19]。Zhao等首先估计代际间隔,然后通过泊松先验的对数似然估计来估计指数增长率,最后通过推导公式得到疫情的基本再生数[20]。Jung等使用马尔可夫链蒙特卡罗方法拟合指数增长模型,然后通过拟合的参数计算基本再生数[21]。Sanche等通过估计指数增长率,结合潜伏期和时间间隔来估计基本再生数[22]。Tang等使用疫情数据拟合代际时间间隔的Gamma分布,并将数据代入到更新方程来估计基本再生数[23]。武文韬等通过有效接触率和感染期,对广东省新冠肺炎疫情的基本再生数进行了估计[24]。李盈科等通过群体的生育率以及矩量生成函数推导出基本再生数[25]。谢家荣等构建了滚动SEIR传播动力学模型,通过新增感染人数和累计感染人数表达式推导出传染病的基本再生数[26]。
梳理上述文献发现,现有主流文献中的传染病传播动力传播模型中均没有考虑疑似者的存在,还假设潜伏者没有传染性。现实中由于技术的短缺,存在大量无法确诊的疑似者,这些疑似者中有一部分人具有传染性。同时,潜伏者也有传染性。本文同时考虑了这些具体的因素而建立新的传染病传播动力学模型。因本模型考虑的问题更符合现实,使用本模型与传统经典模型相比,在同样的情况下对疫情发展的预测会更准确一些。其次,在现有经典文献中,主要从潜伏期、感染期以及指数增长率这些因素和定义角度来计算传染病的基本再生数,这些方法适用于比较简单的传染病模型。现有文献几乎没有学者从无病平衡点的局部稳定性的角度,采用基本再生矩阵推导更复杂情况下的传染病基本再生数的表达式。因基本再生矩阵更适合复杂情况下的传染病传播模型,得到的基本再生数表达式也更能描述传染病的传播能力。最后,现有文献主要是从最小二乘法、智能算法等方法来估计传染病模型的参数,使用马尔可夫链蒙特卡罗方法对传染病模型参数进行估计的学者较少。马尔可夫链蒙特卡罗可以通过随机变量的先验分布,结合数据,得到最接近真实数据的参数后验分布,但马尔可夫链蒙特卡罗算法在执行过程中,无法监测其收敛性程度,因此,有必要设计一个统计指标对马氏链的收敛性进行判别。故本文在这些方面做了一些探索性的工作。本文具体研究思路是,在人群管制模式下,以潜伏者和部分疑似者均具有传染性为前提假设,构建了传染病传播动力学模型,并使用基本再生矩阵理论推导出疫情的有效再生数。同时设计改进的马尔可夫链蒙特卡罗算法估计模型的参数,并进行马氏链收敛诊断,然后进行了仿真模拟,最后分析初始易感者数量和有效接触率对疫情趋势和有效再生数的影响。综上,本文与上述经典文献相比,有以下3点创新:①根据新冠病毒的传播特性,将潜伏者和部分疑似者均具有传染性这两个特征纳入传染病模型中,将SEIR模型拓展为SEDIQR模型,弥补了以前经典文献中模型的不足;②考虑新因素的前提下,使用基本再生矩阵理论推导疫情的有效再生数表达式,这种方法更能揭示疫情发展的内在规律和影响疫情发展的关键因素;③将改进的马尔可夫链蒙特卡罗方法和Geweke方法相结合,这样更能得到符合真实数据的参数后验分布,进而对参数进行估算,弥补了马尔可夫链蒙特卡罗方法收敛性无法判别的缺点。
1 传染病动力学模型
1.1 模型描述
根据人群管制下疫情的现实传播规律,将人群分为易感者、潜伏者、疑似者、隔离者、感染者、康复者6个类别。假设潜伏者在传染期内有传染性,并考虑疑似者的情况,认为部分疑似者也有传染性。假设潜伏者和部分疑似者的传染性与感染者的一样强,首先感染者、疑似者和潜伏者以相同传染性的易感者,将易感者转化为成潜伏者,然后潜伏者以一定的比例成为未确诊的疑似者和确诊的感染者。由于采取了防控措施对疑似者和感染者进行部分隔离,因此,疑似者和感染者中分别有一部分人群进入到隔离者类别中,且隔离者没有传染性。随着对疑似者和感染者的隔离治疗,最终隔离者将会以一定的比例成为康复者和死亡者。人群管制下传染病传播动力学模型示意图如图1所示。

S、E、D、I、Q、R分别表示易感者、潜伏者、疑似者、感染者、隔离者和康复者人数图1 疫情的传播特征
1.2 模型建立
设N为某区域内的总人数,S(t)、E(t)、D(t)、I(t)、Q(t)、R(t)分别为t时刻(天)的易感者、潜伏者、疑似者、感染者、隔离者和康复者人数,β(t)表示随时间变化的疫情有效接触率,它是关于时间t的分段函数,α为疑似者中未确诊感染者所占的比例,ϑ为潜伏者转为疑似者的比例,σ为潜伏者转为感染者的比例,θ表示疑似者转为隔离者的转移率,η表示感染者转为隔离者的转移率,γ表示隔离者的退出率,δ表示疫情的平均死亡率。不考虑出生率、死亡率和人口迁移对疫情传播的影响。那么人群管制下传染病传播动力学模型:

(1)

(2)

(3)

(4)
(5)
(6)
首先定义疫情的有效接触率函数,假设t=τ1之前,疫情的有效接触率为一个常数,即β(t)=β0,在t=τ1之后到t=τ2之前,假设有效接触率快速增加,为β(t)=β1,在t=τ2之后,政府意识到疫情的严重性,如果不加以控制,疫情就会蔓延,因此,对部分疑似者和感染者进行隔离,此时人们之间的接触减少,有效接触率开始下降。假设有效接触率以速率κ进行指数式减少,那么整个疫期内的有效接触率可以用如下的分段函数来表示,即
(7)
1.3 传染病的有效再生数
在人群管制模式下,基本再生数是动态变化的,这时可以用有效再生数来对疫情的传播潜力进行衡量。
结合人群管制下的传染病传播动力学模型以及动态有效接触率函数,可以通过基本再生矩阵的方法求得人群管制条件下的有效再生数。
设x=(x1,x2,…,xn)t为每个人群类别在t时刻的个体数量,且有xi≥0,i=1,2,…,n,无病平衡点为Xs={x≥0|xi=0,i=1,2,…,m},m表示有感染个体的人群类别数量。Fi(x)为人群类别i中新感染个体的比率,Vi+(x)表示以各种方式转换到人群类别i的转换率,Vi-(x)表示从人群类别i转移到其他类别的转换率,Vi(x)=Vi-(x)-Vi+(x)为转移比率。那么传染病传播动力学模型可以表示为
(8)
如果X0为模型式(8)的无病平衡解,那么对于导数dF(X0)和dV(X0),有[27]
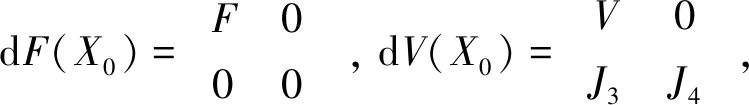
有效再生数可以通过传染病的无病平衡点推导得出,即通过求解下一代矩阵的最大特征值就可以得到有效再生数的表达式。
R(t)=ρ(FV-1)
(9)
由式(1)~式(6)可知,存在感染者的人群类别有4个,分别为E、D、I和Q,因此m=4,那么F、V均为四阶矩阵,对于疫情的无病平衡点有E=D=I=Q=0,设人群管制下疫情的无病平衡点为x0,则x0=(S0,0,0,0,0),为了推导的方便,这里假设模型中的有效接触率为β,那么有
同样计算有
那么FV-1的特征值为
(10)
因此FV-1的谱半径为
(11)
将有效接触率β表示成式(7)所示的依时间变化的形式,以反映不断变化的公共卫生干预措施,那么人群管制下的疫情有效再生数可以表示为
(12)
2 传染病模型参数估计
假设人群管制下潜伏者的传染性与感染者的传染性相同,潜伏者转为感染者的比例σ、感染者转为隔离的转移率η和疫情的平均死亡率δ是已知的(见文献[14]),在上述参数已知的情况下,合理地估计剩余参数β0、β1、k、α、ϑ、θ和γ是对传染病进行预测分析的前提基础。
2.1 Geweke收敛诊断
将马尔可夫链分成若干段,在马氏链前一部分和后一部分渐进独立的假设条件下,Geweke构造的检验统计量近似服从正态分布,比较序列前一部分和后一部分均值的差异,然后构造Geweke检验统计量,如果检验统计量的值介于-2到2之间,认为马氏链是收敛的。Geweke检验统计量为
(13)
式中:E(xs)和V(xs)表示序列开始部分的均值和方差;E(xe)和V(xe)表示序列结尾部分的均值和方差。通过Python的pymc3包的arviz.geweke函数得到收敛诊断结果,如图2所示。
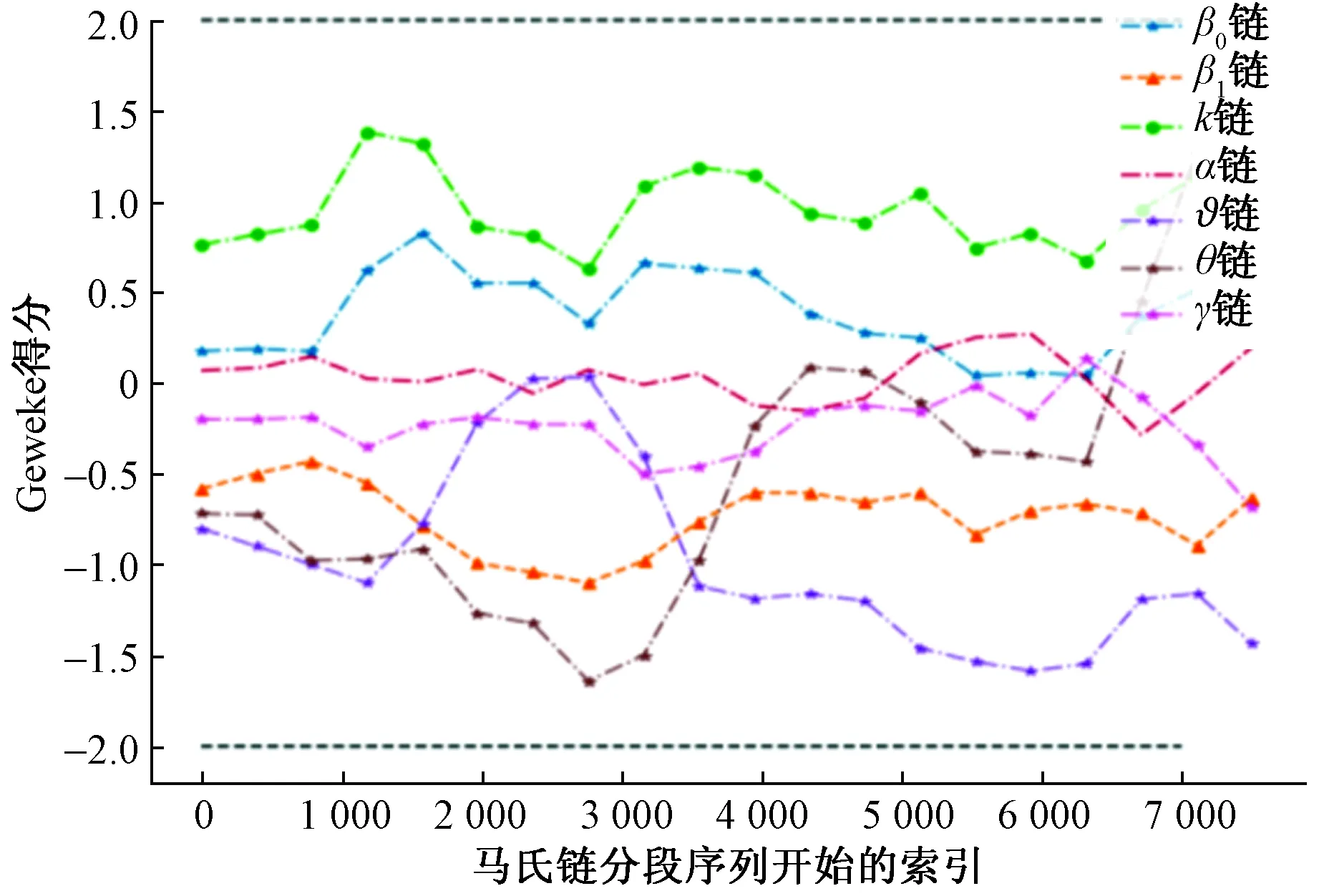
图2 传染病模型参数马氏链的Geweke得分
由图2可知,对于人群管制下传染病传播动力学模型中的被估参数,其马氏链的20个序列段的Geweke得分均在-2到2之间波动,且每个序列的Geweke得分绝对值差异也比较小,说明序列的开始部分和结尾部分参数的均值差异较小,也即各参数的马氏链达到平稳状态,马尔可夫链蒙特卡罗算法达到收敛。
2.2 传染病模型参数估计结果
马尔可夫链蒙特卡罗(MCMC)是一种将马尔可夫链和蒙特卡罗方法相结合的一种无监督机器学习算法,是以马尔可夫链为概率模型的蒙特卡罗方法,马尔可夫链蒙特卡罗方法构造一条马尔可夫链,使其平稳分布为目标分布,进而得到平稳分布的样本,然后依据样本进行蒙特卡罗模拟,从而对随机变量的估计量进行近似数值计算。本小节采用Metropolis-Hastings采样(简称M-H采样)。M-H采样是在MCMC采样的基础上进行了改进,从而解决了MCMC采样可能存在接受概率较低的问题。在对接受概率进行改进之后,就可以采用M-H算法对所需样本进行采样,采样算法如下:
1)首先构造一条马尔可夫链,使平稳分布为目标分布p(x),设置收敛步数为n1,迭代步数为n2。
2)从简单的概率分布函数中获得初始样本值x0。
3)从t=0到t=n2-1进行迭代:
第1步,从条件概率分布(建议分布)Q(x|xt)中获得样本值x*。
第2步,从均匀分布U(0,1)获得一个随机样本值u。

第4步,如果不满足第3步,就拒绝xt+1=x*,则xt+1=xt。
因此样本集合(xn1+1,xn1+2,…,xn2)即为所需样本集。
参数β0、β1、k、α、ϑ、θ和γ的先验分布采用正态分布,建议分布选用多元正态分布,通过Python软件执行M-H算法过程,算法迭代了90 000次,经过了75 000次的燃烧期。程序在Python的jupyter notebook上运行了60 min之后得到结果。各参数的迭代轨迹如图3所示,各参数的结果见表1。
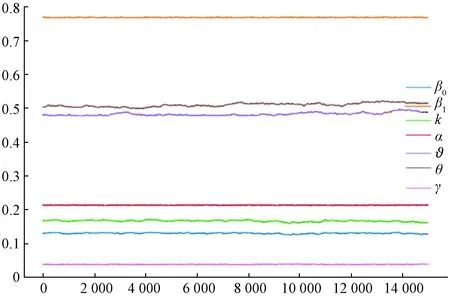
图3 人群管制下传染病模型参数的马氏链轨迹
由Geweke收敛诊断结果和各参数的马氏链轨迹图都可以看出,在经过75 000次的燃烧期之后,各参数的马氏链均达到平稳状态,可以使用平稳分布的样本估算参数的后验均值。由表1可知,β0、β1、k、α、ϑ、θ和γ的后验均值分别为β0=0.129 1,β1=0.767 4,k=0.165 5,α=0.212 3,ϑ=0.481 6,θ=0.508 9,γ=0.037 0。β0、β1、k、α、ϑ、θ和γ的95%HDI分别为[0.126,0.132]、[0.766,0.768]、[0.161,0.169]、[0.211,0.213]、[0.477,0.492]、[0.5,0.519]、[0.036,0.038]。HDI称为最高密度区间,用于估计贝叶斯统计的可信区间,为最小宽度的贝叶斯可信区间(BCI),一般可以表示统计的不确定性。

表1 模型参数估计结果
3 实证分析
以人群控制典型韩国的数据为例。在疫情开始第18天(2020年2月9号,τ1=18)举行礼拜仪式,第31名感染者参与到这次仪式中,导致大规模感染,感染者迅速增加,到第27天(2020年2月18号,τ2=27),第31名感染者确诊,在这之后政府开始采取防控措施应对疫情。
选用2020年1月22日—4月30日的韩国的累计病例数、累计治愈人数、累计死亡人数数据进行实证分析。数据来源于今日头条公布的疫情数据,根据公布的数据画出韩国累计病例数、累计治愈人数、累计死亡人数、现有确诊人数随传播时长的变化趋势如图4所示,新增确诊人数如图5所示。
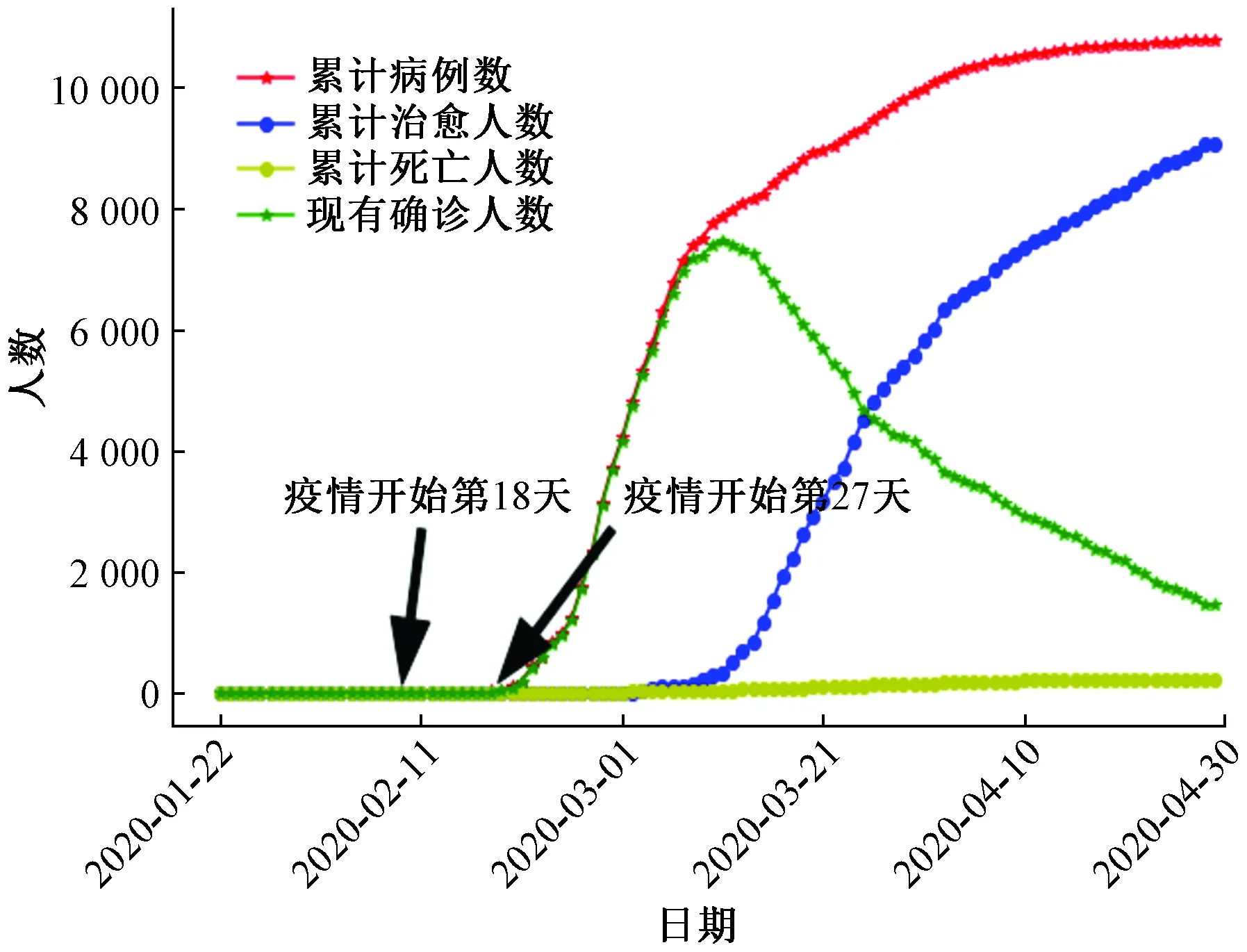
图4 累计病例、现有确诊、累计治愈和累计死亡人数
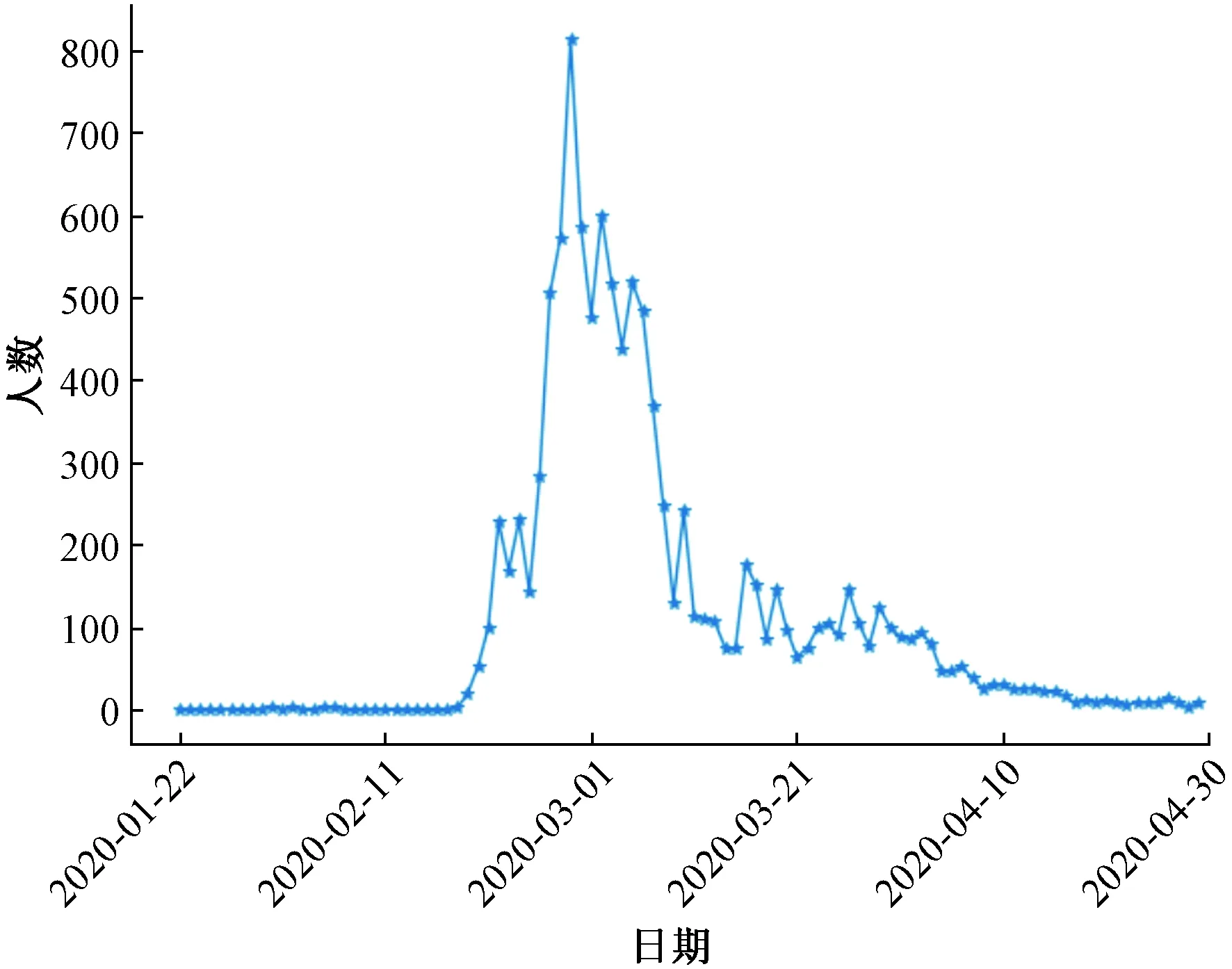
图5 新增确诊人数
由图4可知,韩国在疫情开始第27天(2月18日)之后,累计病例数和现有确诊人数开始迅速增加,在疫情持续大约50天,在3月13日现有确诊人数达到峰值,大约为7 400人左右,之后现有确诊人数开始下降,在4月10日之后,累计确诊病例超过10 000人,之后基本保持平稳。在疫情开始3月1日之后开始有治愈患者出院,随后治愈患者增加的幅度先增加后减小,原因是医院患者先增加后逐渐减小。死亡者的变化幅度不是很大,基本维持在一条水平直线状态,可见韩国政府的防控措施取得了很大的效果。
由图5可知,在疫情开始一个月之前,新增确诊人数整体变化不大,在一个月之后,新增人数迅速增加,在3月1日左右,新增人数达到峰值,约为810人,之后新增人数整体开始出现下滑,在4月10日之后,新增人数总体上保持平稳的状态。
将模型计算结果与实际值进行拟合,得到模型预测的住院患者与现有确诊人数的拟合图,如图6所示,并得到模型预测的感染者人数和康复者人数变化趋势,如图7所示。

图6 确诊人数模型值与实际值拟合结果
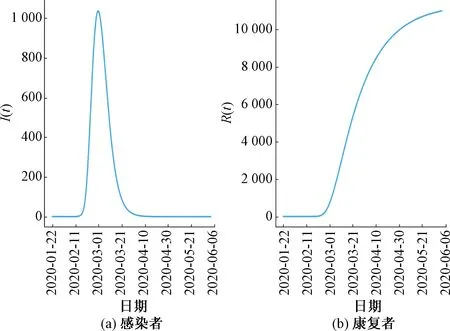
图7 模型预测的感染者和康复者
由图6可知,韩国预计在3月下旬,现有确诊人数达到峰值,约为7 000人左右,韩国约在3月1日左右疫情开始出现拐点,在6月初,随着大量的住院患者被治愈,韩国的现有确诊人数逐渐减小,接近于0。模型得出的现有确诊人数的预测曲线与实际情况基本一致。由此说明,使用人群管制下的传染病传播动力学模型来预测韩国疫情,具有比较好的预测效果,从而验证了所建立的模型的有效性。
由图7(a)可知,韩国的感染者在2月中旬之前并没有明显的变化,在2月中旬之后,感染者迅速增加,在3月1日左右,感染者人数到达峰值,超过1 000人,之后开始下降,大约在4月10日,感染者人数减少到0。由图7(b)可知,在2月下旬之前,还未有患者被治愈,在2月下旬之后逐渐有康复者出现,并且康复者增加的速率先增大后减小,6月初,康复者人数超过10 000人,之后进入平稳阶段。
将估计的参数和已知参数代入到人群管制下的有效再生数和有效接触率表达式中,可以得到R(t)和β(t)随时间t的变化趋势,如图8所示。

图8 疫情有效再生数和有效接触率的变化趋势
由图8(a)可知,在疫情开始20 d之前,人群管制下的有效再生数是一个恒定不变的常数。在20 d之后到27 d左右,有效再生数也是一个恒定不变的常数,但比其疫情开始20 d之前的有效再生数高。在第1阶段有效再生数接近于1,在第2阶段有效再生数迅速增加,将近于6。此时政府应该保持高度重视,如果不采取措施加以应对,疫情有大范围爆发的风险。从此之后,政府开始意识到疫情的严重性,采取了疫情防控措施,有效再生数开始下降。在疫情开始大约37 d左右,有效再生数降到1水平以下。说明政府的防控策略有了比较明显的效果,疫情有逐渐缓解最后达到消亡的趋势。
由图8(b)在疫情开始20 d之前,人群管制下的动态有效接触率是一个常数。在疫情开始20 d到大约37 d左右,动态有效接触率有所上升,但也是一个常数,之后动态有效接触率开始下降。
比较图8(a)和图8(b)以发现,人群管制下疫情的有效再生数和动态有效接触率有着密切的联系,并且两者之间的变化趋势是一致的,而有效再生数能够反映疫情的传播能力。因此,如何控制减小动态有效接触率从而减小疫情的有效再生数,降低疫情的传播能力和传染风险,是政府管理部门和医疗专家值得思考的问题。
4 疫情的管控力度分析
4.1 管控力度对疫情发展趋势的影响
传染病的传播方式主要为接触传染,一般是感染者接触易感者进行传染的。因此,只有阻断人与人之间的传播,实施一系列公共卫生干预措施,才能真正有效地控制和遏制新冠病毒的爆发。初始易感者是指在某个疫情开始的节点,在一个传染病系统中所存在的易感者数量,其数量的多少对于疫情的发展具有重要的影响。接触数是衡量接触程度的重要指标,能够从侧面反映传播风险的大小,减小这两个指标的值对于减小传播率、降低传播风险进而降低疫情的蔓延势头具有重要的意义。在传播概率不变的情况下,接触数与有效接触率成正比。不同的初始易感者数量S0和有效接触率β1对于确诊人数和感染者发展趋势的影响程度如图9和图10所示。易感者的管控力度对疫情峰值和峰值时间的影响见表2,有效接触率的管控力度对疫情峰值和峰值时间的影响见表3。

图9 不同系数的S0对韩国现有确诊人数和感染者的影响

图10 不同系数的β1对韩国现有确诊人数和感染者的影响

表2 易感者的管控力度对疫情峰值和峰值时间的影响

表3 有效接触率的管控力度对疫情峰值和峰值时间的影响
1)由图9(a)和表2可知,若将初始易感者数量扩大为原有初始易感者数量的1.1倍时,现有确诊人数在前期增加的幅度最大,且峰值最高,超过了25 000人。在疫情开始约51 d到达峰值,峰值时间是最晚的,且现有确诊人数达到峰值后下降的速率也最快。若将初始易感者的数量缩小为原有初始易感者数量的0.7倍时,其现有确诊人数的峰值是最小的,只有100多人。在疫情的第48天到达峰值,峰值时间是最早的。且疫情前期现有确诊人数的增加幅度最慢,到达峰值后下降的速率也最慢。由此可以发现这样的规律,随着对易感者管控力度的加强,确诊人数峰值时间是越来越早的,峰值人数是越来越小的。前期确诊人数增加的幅度越来越小,到达峰值后人数下降的幅度也越来越小。从图9的曲线形状来看,初始易感者数量对于确诊人数的影响是非常敏感的,较小的变动对于其人数的变化是非常大的。
由图9(b)和表2可知,若将初始易感者数量扩大为原有初始易感者数量的1.1倍时,感染者的人数在峰值之前的增长幅度最快,峰值也最高,将近2 000人。在疫情第40天到达峰值,并且在到达峰值之后的感染者下降速率也最快。若将初始易感者数量缩小为原来的0.7倍时,感染者在峰值之前和峰值之后的增长和下降速率都是最慢的,且在疫情第37天到达峰值。并且随着对易感者管控力度的加强,感染者峰值时间越来越早,峰值人数也越来越小。初始易感者的数量对于感染者的影响也是非常敏感的。
2)由图10(a)和表3可知,若将有效接触率扩大为初始有效接触率的1.1倍时,现有确诊人数在前期增加的幅度最大,且峰值最高,多于20 000人,峰值时间也是最晚的。且确诊人数达到峰值后下降的速率也最快,但疫情结束的时间晚于其他接触数下的现有确诊人数曲线。若将有效接触率数量缩小为原来的0.7倍时,其确诊人数的峰值是最小的,约为300人左右,峰值时间是最早的。且疫情前期确诊人数的增加幅度最慢,到达峰值后下降的速率也最慢。由此也可以发现这样的规律,随着对有效接触率管控力度的加强,现有确诊人数峰值时间是越来越早的,峰值人数是越来越小的,前期现有确诊人数增加的幅度越来越小,到达峰值后人数下降的幅度也越来越小。
由图10(b)和表3可知,若将有效接触率扩大为原来的1.1倍时,感染者的人数在峰值之前和峰值之后的增长和下降速率都是最快的,且峰值最高,将近3 000人,在疫情开始约51 d达到峰值。若将有效接触率缩小为原来的0.7倍时,感染者的人数在峰值之前和峰值之后的增长和下降速率都是最慢的,且峰值最小,不到100人,约在疫情开始37 d到达峰值。因此,随着对有效接触率管控力度的加强,感染者的峰值越来越小,峰值达到时间越来越早。
3)结合图9和图10,表2和表3可以发现,当对初始易感者和有效接触率实施相同的管控力度时,不影响现有确诊人数和感染者的峰值时间,但是对峰值大小却有比较明显的影响。当初始易感者数量和有效接触率呈现同幅度下降时,初始易感者数量对于缓解疫情发展具有更大的作用。
4.2 管控力度对有效再生数的影响
有效再生数是衡量疫情传播能力的重要阈值参数,有效再生数大于1说明疫情有进一步蔓延的趋势,有效再生数小于1说明疫情有所缓解直到消亡。从人群管制下有效再生数的表达式可以看出,初始易感者数量和有效接触率对有效再生数有很大的影响。不同的初始易感者数量和有效接触率对有效再生数的影响程度如图11和图12所示。

图11 不同系数的S0对有效再生数的影响
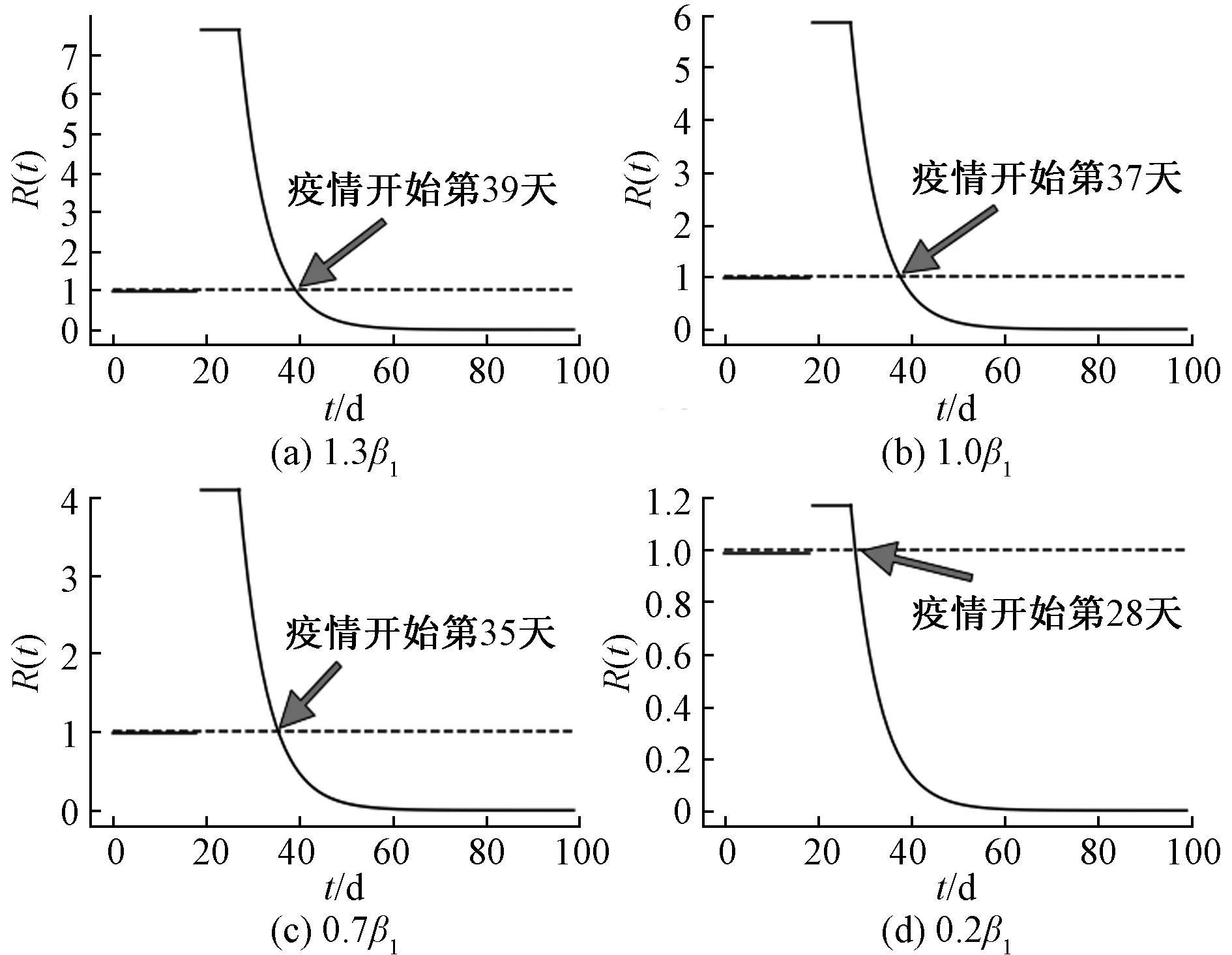
图12 不同系数的β1对有效再生数的影响
1)由图11可知,若将初始易感者的数量扩大为原有初始易感者数量的1.3倍时,在疫情开始到第18天,有效再生数是不到2的常数。在疫情开始第18天到27天,有效再生数继续增加,说明在此时疫情开始蔓延,之后由于政府采取了疫情防控措施,有效再生数开始以指数形式下降,疫情蔓延的速度有所下降。在疫情开始第39天之后,有效再生数处于1水平以下,说明此时疫情开始有所缓解并逐渐消亡。若将初始易感者的数量缩小为原有初始易感者数量的0.2倍时,在疫情开始到18天,有效再生数小于1,此时说明疫情并没有流行开来。在疫情开始第18天到27天,有效再生数有所上升,并超过了1,之后开始下降,在疫情开始28天之后,有效再生数小于1。由此可以发现,随着初始易感者数量占原来初始易感者数量比例的减少,有效再生数变化趋势并未改变,但在[0,τ1]和[τ1,τ2]这两个时间段的有效再生数随之下降,有效再生数下降为1所需的时间也越来越短。
2)由图12可知,若将接触数扩大为原有接触数的1.3倍时,在疫情开始到第18天,有效再生数保持在1左右。在疫情开始第18天到第27天,有效再生数超过7,之后有效再生数开始下降。在疫情开始第39天之后,有效再生数下降到1以下。若将接触数缩小为原有接触数的0.2倍时,在疫情开始到第18天,有效再生数接近于1,在疫情开始第18天到第27天,有效再生数接近于1.2,此时疫情开始蔓延。在疫情开始第28天之后,有效再生数处于1以下。由图形趋势可以发现,随着有效接触率占原来有效接触率比例的减少,在[0,τ1]和[τ1,τ2]时间段的有效再生数保持不变。但在τ2之后有效再生数开始下降,并且有效再生数下降到1时所需的时间也越来越短。
3)比较图11和图12可知,对初始易感者数量和有效接触率实行同样的管控力度时,不会影响τ1时间之后有效再生数的变化,也不会影响有效再生数降为1所需的时间,但对[0,τ1]时间段的有效再生数影响却不同。
5 结论
本文综合考虑人群隔离、潜伏者和部分疑似者均具有传染性的因素,构建了人群管制模式的传染病传播动力学模型,以此来预测疫情的发展趋势和不同的管控力度对疫情发展和有效再生数的影响程度。通过有效再生数的推导、模型参数估计和实证分析得到以下几点结论:
1)结合人群管制的特点,加入隔离者、考虑潜伏者和部分疑似者均具有传染性这3个具体因素而建立的传染病动力学模型,能够很好地描述人群管制下疫情的传播规律,所建立的模型是有效且合理的。因建立的模型更符合人群管制模式下的疫情传播,得到的预测结果相对于文献[14]对韩国的疫情预测会更准确一些。
2)基本再生矩阵理论依据无病平衡点的局部稳定性,能够很好地推导出人群管制下的有效再生数表达式,得出的有效再生数变化曲线也反映了人群管制下的疫情传播能力,说明相对于文献[21-23,25]使用指数增长率、感染期和潜伏期来计算基本再生数,基本再生矩阵更能够科学合理地推导出传染病的临界阈值。
3)马尔可夫链蒙特卡罗方法是将马尔可夫链与蒙特卡罗相结合的一种无监督机器学习算法,是在贝叶斯理论框架下通过计算机进行动态模拟的蒙特卡罗方法,主要应用于求概率模型中未知参数的后验分布,从后验分布中采样以构造最接近真实数据的概率分布的一种方法。马尔可夫链蒙特卡罗方法相对于最小二乘等优化方法,能够有效地寻找到真实的参数后验,其不失为一种理解性高,逻辑性强的参数估计方法。
4)从管控力度对疫情发展影响的分析结果可知,减小初始易感者数量和有效接触率均能够降低疫情现有确诊人数和感染者的峰值,且能够缩短到达峰值所需的时间。有效接触率和初始易感者数量都是现有确诊人数和感染者人数变化的重要敏感参数,两者相辅相成。减少初始易感者的数量从另一方面也可以减少有效接触率,减少有效接触率也可以通过减少初始易感者的数量来实现,它们对疫情的发展都有重要的影响。当初始易感者数量和有效接触率呈现同幅度下降时,初始易感者数量对于缓解疫情发展具有更大的作用。从管控力度对疫情有效再生数的影响结果可知,减小初始易感者数量和有效接触率均能够缩短有效再生数降为1所需的时间,说明减小初始易感者数量和有效接触率能够有效地缓解疫情的蔓延。从各国现实疫情管控效果来看,东方比西方管控得要好。原因就在于东方国家(韩国是个典型)比西方国家(美国是个典型)更重视对疫情初期对有效接触率和初始易感者数量的控制。从某种角度来说,美国在拥有全世界最强大的医疗设施条件下,对疫情管控的效果却成为最差的国家之一,与其初期不按科学原则管控疫情有关。他们为其他国家管控类似的疫情提供了反面教材,这也是世界各国应该汲取教训的地方。本研究为今后在世界范围内控制类似疫情提供了理论和事实依据。
本文在人群管制条件下,将潜伏者和部分疑似者均具有传染性这一特点考虑进模型,比其他的学者考虑问题更全面,更接近客观现实,因此,预测的效果与现实结果相比较,拟合的效果更好。但没有考虑新冠疫情中一些无症状感染者的情况,所以预测结果与现实还有一定的出入。另外,假设潜伏者和部分疑似者传染率与感染者的传染率相同,这一假设并没有现实的数据支撑,将在后期进一步对此展开研究,并将新的研究完善到模型中去。
