Photon subtraction-based continuousvariable measurement-device-independent quantum key distribution with discrete modulation over a fiber-to-water channel
2022-03-23ChaoYuYinLiJianzhiDingYunMaoandYingGuo
Chao Yu, Yin Li, Jianzhi Ding, Yun Mao,* and Ying Guo,3,*
1 School of Computer Science and Engineering, Central South University, Changsha 410083, China
2 School of Automation, Central South University, Changsha 410075, China
3 School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876,China
Abstract We propose a discrete-modulated continuous-variable measurement-device-independent quantum key distribution protocol over a fiber-to-water channel.Different from optical fibers,the underwater channel has more severe optical attenuation because of optical absorption and scattering,which reduces the maximum communication distance.To enhance the performance of the protocol, the photon subtraction operation is implemented at the modulator side.We carry out a performance simulation in two different kinds of seawater channel, and the result shows that the scheme with photon subtraction has a longer secure communication distance under certain conditions.
Keywords: measurement-device-independent, discrete modulation, fiber-to-water channel,continuous variable, quantum key distribution
1.Introduction
Quantum key distribution (QKD) [1, 2] is one of the most important applications and rapidly developing technologies of quantum encryption.Whilst it is distinct from classic communication,the safety of QKD is built on the physical properties of photons and it can achieve unconditional security [3–5].Generally, there are two types of QKD, discrete-variable QKD(DVQKD) and continuous-variable QKD (CVQKD) [6, 7].Thanks to its simplicity in experiments and higher performance over short distances,CVQKD has become a research hotspot in recent years.In the Gaussian-modulated CVQKD (GMCVQKD),the information follows Gaussian distribution so that it is more susceptible to noise than binary data, which limits the maximum communication distance[8,9].To solve this problem,discrete-modulated CVQKD(DM-CVQKD)was proposed[10].In the DM-CVQKD, secret key data is binary, and it is modulated on two orthogonal components of the optical field [11],which shows better robustness to noise and better performance at long distances compared with GM-CVQKD.
In the one-way CVQKD scheme,there is an assumption that the hardware of QKD such as the detector is ideal, and most studies rely on this assumption.However,such a perfect device is difficult to achieve in reality,and this has led to numerous attacks on vulnerabilities caused by device imperfections,which include LO fluctuation attacks, wavelength attacks, detector saturation attack[12–14],etc.To solve the security loopholes caused by the imperfection of the measurement device,the continuous variable measurement-device-independent (MDI) quantum key distribution (CV-MDI-QKD) has been proposed [15–18].In the CVMDI-QKD protocol, there are three parties involved in the key distribution including the legitimate communication parties Alice,Bob and an additional untrusted third party, Charlie.Unlike traditional one-way QKD with only one sender, there are two signal senders,Alice and Bob in CV-MDI-QKD.In this protocol,Alice and Bob both send signals to Charlie,and Charlie performs Bell-State Measurement on the quantum signals that passed through the quantum channels [19].Bob manipulates his quantum state according to the measurement result of Charlie,and then Alice and Bob receive a string of correlated data.
However, what is unfortunate is that the CV-MDI-QKD protocol has a shorter secure transmission distance compared with the traditional one-way CVQKD protocol [20].Photon subtraction (PS) is one of the non Gaussian operations that have been proven to enhance the entanglement degree of quantum state and thereby improve the security distance[20–23].This operation can be implemented with prior art and it has been applied in the experiment [24].In order to extend the maximum communication distance, we apply the PS operation after signal modulation at Alice’s side.
In the existing research,optical fiber is the primary channel of a CVQKD scheme.Nevertheless, underwater CVQKD has been widely concerned in recent years for its extensive application prospect, especially in the military field [25].However,due to the attenuation and absorption of light, the maximum safe distance of quantum signal transmission in seawater is much shorter than that in optical fiber.Fortunately,underwater CVQKD still has important application scenarios.We consider that in some cases, a CV-MDI-QKD scheme may work in different channels.Optical fibers have much less impact on quantum signals than atmospheres.However, for one-way CVQKD,it is difficult to inject the quantum signal in the optical fiber directly into water,so we chose to use the MDI scheme to make Charlie a mediator to connect fiber and water channels.In this paper, we analyze the different channel medium of Alice and Bob to Charlie in a CV-MDI-QKD scheme.We also assessed the factors of seawater that affect the maximum distance and applied the PS operation to enhance the performance of the underwater CVQKD scheme.
This paper is structured as follows: In section 2, we discuss the CV-MDI-QKD scheme with PS.In section 3, we analyze the influence factors of seawater channel.In section 4, we show the performance of the proposed scheme with simulation.Finally,we draw the conclusion in section 5.
2.DM CV-MDI-QKD with photon subtraction
In this section,we first introduce the discrete modulation CVMID-QKD protocol, including the prepare-and-measurement(PM)scheme and the entanglement-based(EB)scheme which is equivalent to the PM version in security.Afterwards we interpret the PS operation and its application in the discrete modulation CV-MDI-QKD.
2.1.Discrete modulation CV-MDI-QKD
The PM scheme of the discrete modulation CV-MDI-QKD is illustrated in figure 1.In the PM scheme, Alice and Bob prepare two coherent states A and B independently and send them to an untrusted third party named Charlie.Then Charlie measures the two states and the results are C and D.Afterwards, Charlie makes public the results and Bob manipulates his coherent state according to the published results to make it associated with Alice.Finally, Alice and Bob perform the post-processing steps to get the security key.The EB of our scheme is shown in figure 2.Here, we suppose that the channel between Alice and Charlie is called CAC, and is called CBCbetween Bob and Charlie.The length of channel CACand CBCis represented by LACand LBCrespectively,and the transmittance of CACand CBCis TAand TBrespectively.To simplify the proof of security, we concentrate on the EB scheme and describe its process in detail.
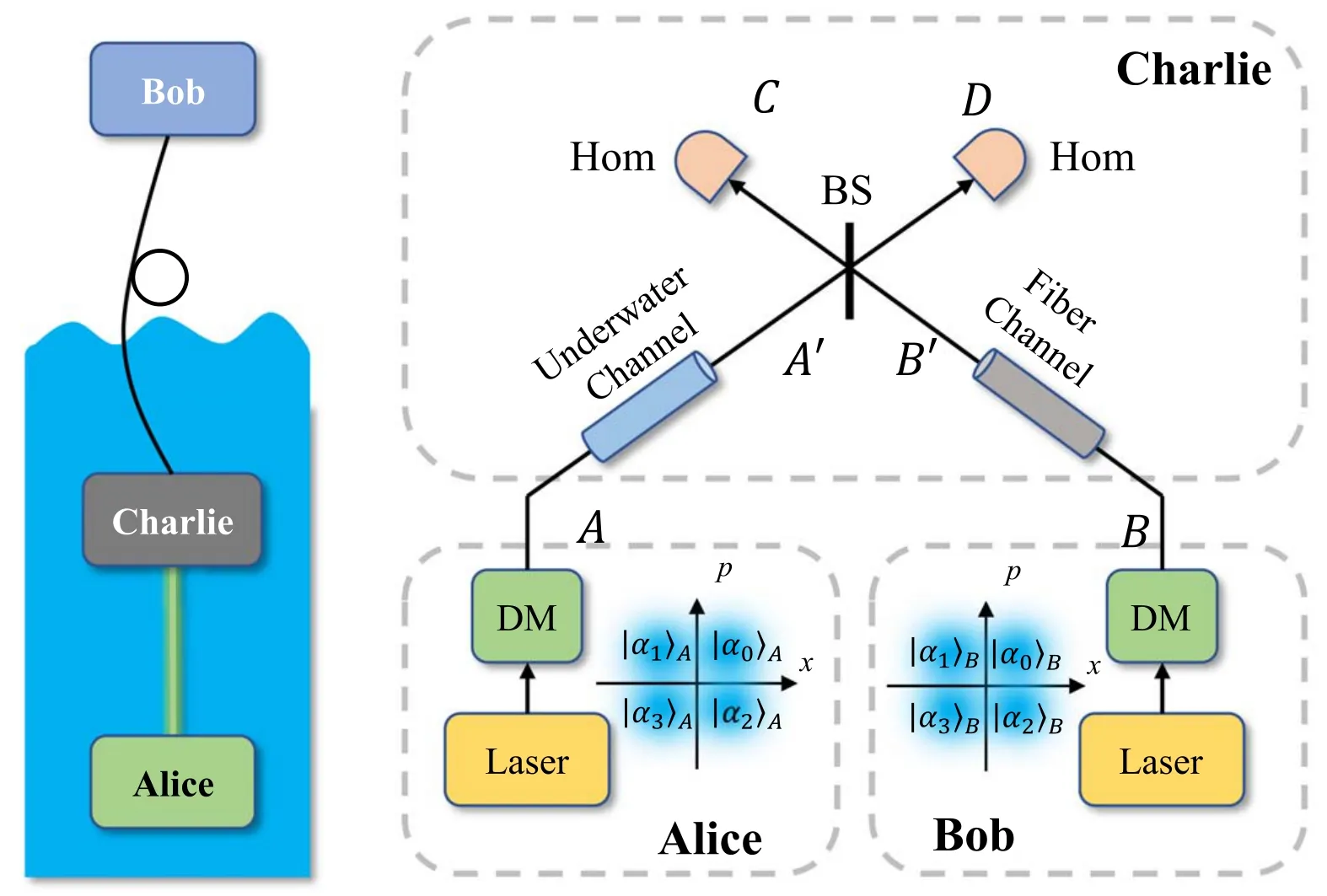
Figure 1.The PM scheme of discrete modulation CV-MDI-QKD.DM is the discrete modulation; Hom is the homodyne detection; BS is beamsplitter.
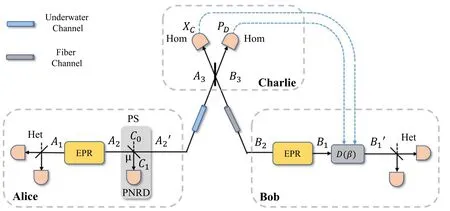
Figure 2.The EB scheme of PS-based discrete modulation CV-MDI-QKD.PNRD is the photon number resolving detector; D(β) is the displacement operation; Het is the heterodyne detection; Hom is the homodyne detection.
whereρB1represents the density matrix of mode B1and β=g(XC+iPD)where g is the gain of the displacement operation [26].After the displacement operation, mode A1andB1′ are entangled, and the secret key data of Alice and Bob are interrelated.
(vi) Alice and Bob perform the post-processing steps to share the secret key, which include data reconciliation,parameter estimation and privacy amplification.
After the above steps, Alice and Bob complete a key distribution process.However, due to the characteristics of the MDI protocol, the security transmission distance of key distribution is generally shorter than that of a one-way CVQKD protocol [27, 28].So in the following section, we use PS to increase the security transmission distance.
2.2.PS-based discrete modulation CV-MDI-QKD




Figure 3.The light intensity distribution after transmitting in (a) pure sea water and (b) clean ocean water.The transmission distance is 2 meters and the power of source is 10 mW.

where

and the detailed calculation is shown in [31].The asymptotical secret key rate of PS-based scheme against collective attacks is expressed as
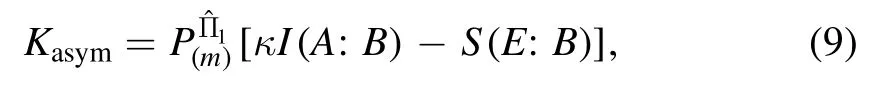

where χA=1/TA-1+εAand χB=1/TB-1+εB.To minimize the excess noise εth, we set the value of g to

and then εthcan be expressed as
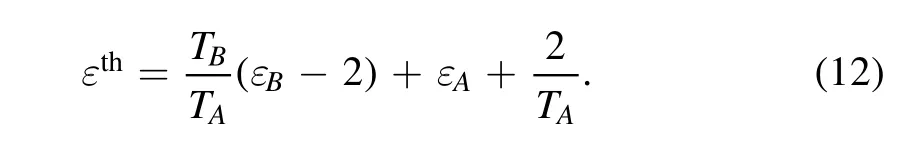
Details for the calculation of the secret key rate can be found in appendix A.After the PS operation,modeinstead of A2will be sent to Charlie through the quantum channel, and the follow-up progress is the same as the original discrete modulation CV-MDI-QKD.
3.Underwater channel
In the most studies on QKD, researchers analyze the CVQKD system in the fiber quantum channel.To explore the performance of our protocol, we first need to analyze the underwater channel.
Now we examine the influence of the seawater channel on the transmitted signal pulses.Due to the presence of water molecules, dissolved and suspended impurities (such as dissolved organic matter and chlorophyll molecules)in seawater[33],the transmission of light in the seawater channels is very difficult, resulting in the transmission distance being several orders of magnitude lower than the former.At the same time,the characteristics of seawater channels are also influenced by temperature and salinity.In figure 3, we show the light intensity distribution after transmitting in seawater [34–36],where the transmission distance is 2 meters and the power of the source is 10 mW.We have determined that after passing through the seawater channel, the light intensity is weakened and relatively serious scattering occurs.Since the transmission distance is short, we suppose that the channel is in the identical composition of seawater and hence it becomes a linear channel [25, 37–39].Therefore, the transmittance ofseawater channel can be expressed as

Table 1.Attenuation coefficient of seawater at 520 nm wavelength.

whereD is the depth,λ is the wavelength of light and c is the total attenuation coefficient.There are two main factors that affect the light transmission in seawater: absorption and scattering.Absorption refers to the energy loss of light caused by the interaction between photons and particles in seawater,which leads to the reduction of light intensity.Scattering means the change of movement direction of photons when they interact with other particles.Consequently, the total attenuation coefficient can be written as [38]:
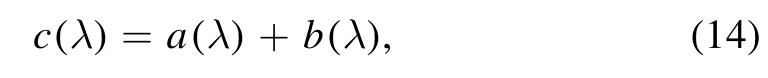
where a(λ) denotes the absorption coefficient and b(λ)denotes the scattering coefficient.The influence of temperature, salinity and chlorophyll concentration on the attenuation coefficient is shown in appendix A.
However, in practical terms, the model becomes more complex and even difficult to estimate, considering the effect of solutes, suspended solids, background light and others on the attenuation coefficient.Fortunately, some researchers have come up with valid parameters through underwater experiments, and we can use these data directly, which also makes our results more practical.Because the attenuation of light at different wavelengths is various, we choose the least attenuated blue-green light (520 nm) for communication purposes.The attenuation coefficient and corresponding sea water types are shown in table 1 [40].
4.Performance analysis
In this section, we discuss the performance of the proposed scheme in the asymptotic cases.Generally, four-state and eight-state modulation protocols are most often used in discrete modulation CVQKD.To simplify the analysis, for the PS operation we only consider its implementation in the fourstate modulation scheme in the following.
The modulation variance VMhas a significant impact on performance.In figure 4, we show the relation between VMand the secret key rate.The solid lines represent the eightstate protocol and the dash lines represent the four-state protocol.The black, red and blue lines represent LAC=0 m,LAC=10 m and LAC=20 m in figure 4(a) and LAC=0 m,LAC=5 m and LAC=10 m in figure 4(b) respectively.In order to make the security analysis method in Gauss-modulated CVQKD still applicable, the variance needs to be set in a small range (Vm≤0.5) [10].At the same time, to facilitate the comparison with the original discrete modulation CVMDI-QKD scheme,we set the constant variance with it in the following simulation.
The asymptotic secret key rate as a function of LACin different seawater channel is illustrated in figure 5.Compared with the original discrete modulation CV-MDI-QKD scheme,the one-photon subtracted (1-PS) scheme has higher secret key rate in the long distance when LBC=0 m,10 m and 20 m,although its performance is lower when the communication distance is short due to the low success rate of PS.Besides,the success rate of PS operation decreases with the rise of subtracted photon number m [21], resulting in that the secret key rate of m-PS (m >1) scheme always lower than onephoton subtraction scheme.Therefore, we only discuss the one-photon subtraction scheme in the following.
According to [41], the impact of underwater turbulence on CVQKD system can be reflected in the transmittance.When the communication distance is long, in other words,when T is low,the PS-based scheme has a higher performance than the original scheme.That is, even in the presence of underwater turbulence, our PS-based CV-MDI-QKD scheme is still helpful for performance.However, we find from figure 6 that although the PS-based scheme has a longer secure transmission distance when the LBCwas short, the performance of PS-based scheme would be lower than the original four-state scheme when LBCis greater than a certain value.The reason for this phenomenon may be that the total channel noise increases with the increase of LBC, and the variance of the quantum state may decrease after PS.
5.Conclusion
We have suggested a method to enhance the performance of a fiber-to-water discrete modulation CV-MDI-QKD scheme by utilizing a PS operation and simulating it in two different fiber-to-water channels,and the PS operation was described in detail.We assessed the factors that affect the underwater light transmission and used the optimal parameters in the simulation.The influence of modulation variance is also considered,and for comparison we chose the same variance, which is VM=0.5, in the original and proposed protocol.The simulation results show that the proposed scheme has a longer transmission distance when LBCis short, but lower performance than the original protocol in the long LBCcase.The transmission distance of the underwater channel is several orders of magnitude shorter than that of the optical fiber channel.However,it is still of great value in the construction of underwater communication networks.
Appendix A.Calculation of asymptotic secret key rate
In this section,we discuss the properties of the quantum states transmitted in the PS-based discrete modulation CV-MDIQKD scheme and the calculation method of the secret key rate in the asymptotic scenario.We suppose that Alice employs heterodyne detection while Bob employs heterodyne detection, and the postprocessing uses reverse reconciliation.The EPR state |ψ〉 prepared by Alice and Bob in the traditional DM-CVQKD can be written as
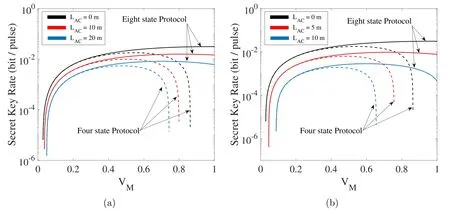
Figure 4.The secret key rate as a function of modulation variance VM in (a) pure sea water and (b) clean ocean water.The solid lines represent the eight-state protocol and the dash lines represent the four-state protocol.The parameters are as follows: εA=εB=0.001 and LBC=0 m.

Figure 5.The secret key rate as a function of LAC in(a)pure sea water and(b)clean ocean water.The solid lines represent the PS-based fourstate CV-MDI-QKD protocol,the dash lines represent eight-state CV-MDI-QKD protocol and the dot lines represent the original four-state protocol.The color of lines black, red and blue represents LBC=0 m, LBC=10 m and LBC=20 m respectively.

where d=4 for four-state protocol and d=8 for eight-state protocol.Here,
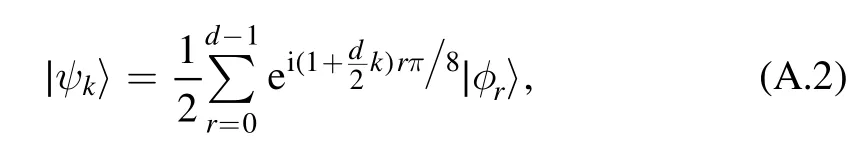
and
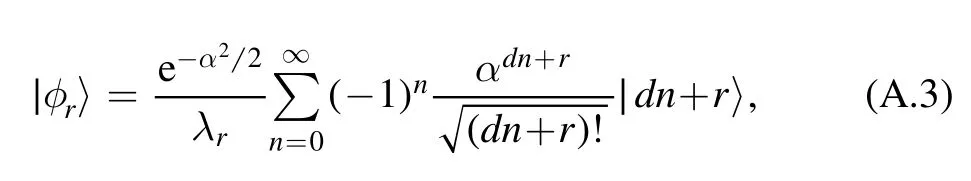
where r=0, 1, …, d-1.For four-state protocol, λris given as
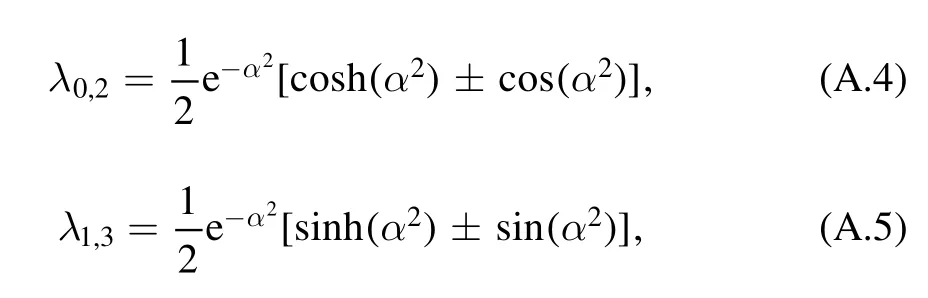
and for eight-state protocol, λris given as
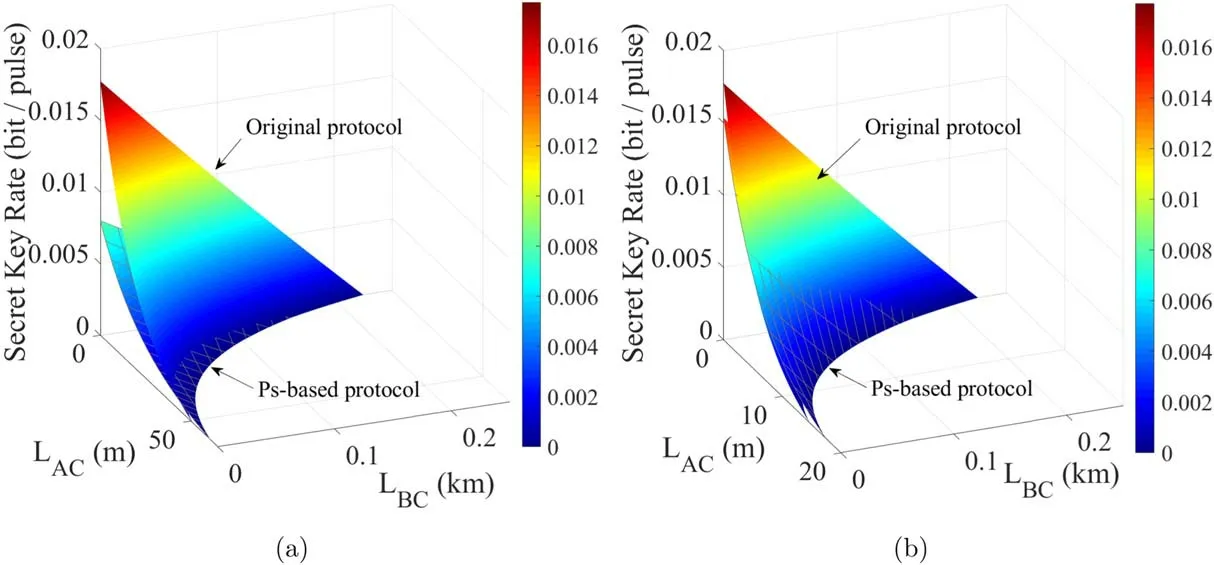
Figure 6.The secret key rate as a function of LAC and LBC in (a) pure sea water and (b) clean ocean water.The respectively.The smooth surfaces and the grid surfaces represent the original four-state CV-MDI-QKD and the corresponding PS-based scheme respectively.
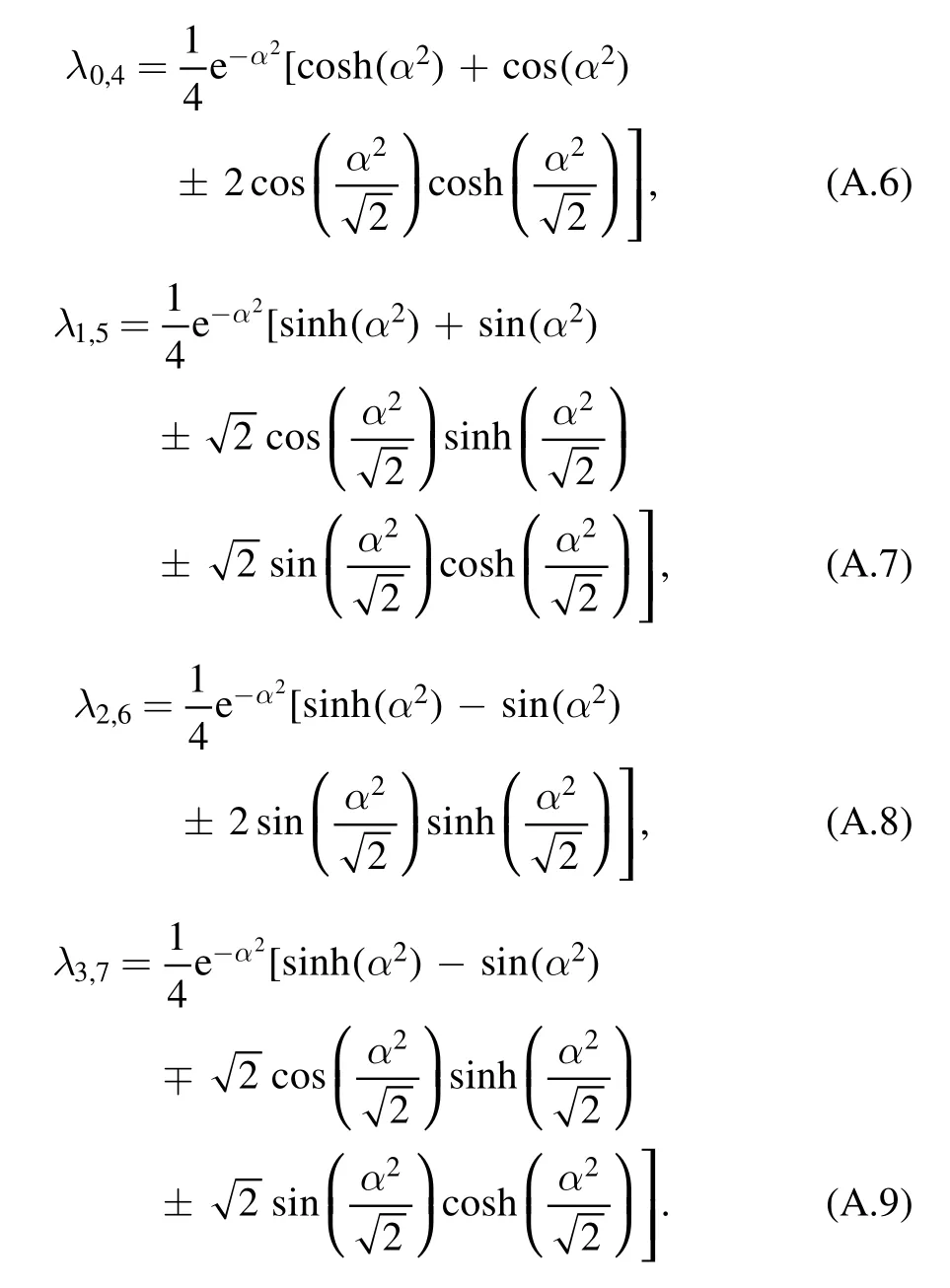
After the transmission of quantum channel and the detection of Charlie,the co-variance matrix of statecan be represented as
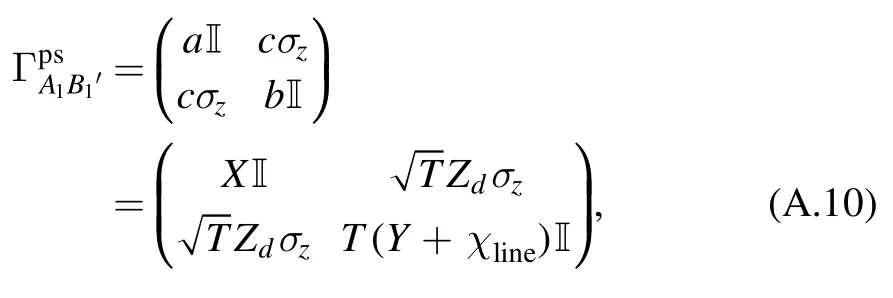
where X,Y and Zdare given in equation(6)–(8).The Shannon mutual information between Bob and Alice is calculated by
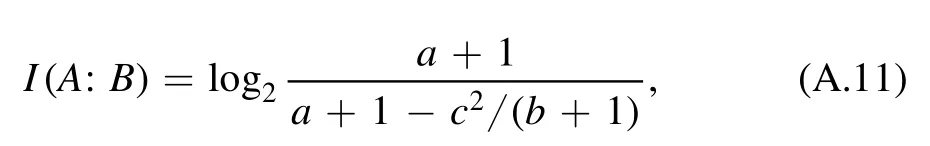
and the Holevo bound S(E:B) is

whereG(x) = (x+ 1) log2(x+ 1) -xlog2x,which denotes the Von Neumann entropy.Here, γ1,2,3are the symplectic eigenvalues derived from covariance matrix and they are calculated by

where A=a2+b2-2c2and B=ab-c2.Then, we can calculate the secret key rate by equation (9).
Appendix B.Description of partial influencing factors of seawater channel
In this section we describe the effects of temperature,salinity and chlorophyll concentration on the marine channel.Assuming that the current channel is pure seawater, considering the influence of temperature and salinity, the absorption coefficient can be calculated as [42]:
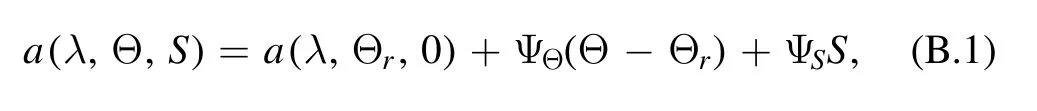
where Θ is the temperature,Θris a reference temperature,S is salinity and ΨΘ,ΨSis the linear temperature slope and salinity slope respectively (See [42] for detailed calculation).According to [43], the scattering coefficient can be further expressed as

Here, bd(λ, Θ, S) and bc(λ, Θ, S) can be calculated by

where k is the Boltzmann constant,NAis the Avogadro number,ρ is the density, n is the refractive index in vacuum, βΘis the isothermal compressibility, δ is the depolarization ratio of the solution,and awand Mware the activity and molecular weight of water in the solution respectively, which are detailed in [43].
The effect of chlorophyll on attenuation coefficient can be expressed as [37]:

where aw(λ)is the absorption coefficient of pure water, ac(λ)is a nondimensional, statistically derived chlorophyll-specific absorption coefficient.
杂志排行
Communications in Theoretical Physics的其它文章
- Thermal currents obtained and mutually switched by a modified Haldane model in graphene
- Effect of layer sliding on the interfacial electronic properties of intercalated silicene/indium selenide van der Waals heterostructure
- Nonequilibrium effects of reactive flow based on gas kinetic theory*
- Preferential attachment network model with aging and initial attractiveness
- A classical density functional approach to depletion interaction of Lennard-Jones binary mixtures
- A residual-based message passing algorithm for constraint satisfaction problems
