压电式马达变量控制系统的研究

李峙毅，林晓焕，陈勇洁，吕广雷，罗 岩

(西安工程大学机电工程学院，陕西 西安 710048)

0 引言

随着石油、煤炭等传统不可再生能源的日渐匮乏，全球性的能源危机已成为当前世界各国密切关注的焦点。以水能、电能和太阳能为代表的洁净可再生能源成为了解决能源问题的关键。但是，风能的间歇性以及太阳能的周期性会导致输电的不稳定性。水能连续、稳定的优点由此凸显[1]。我国作为自然水资源储备丰富的国家，储藏着巨大的能量。无论是低能流密度海域的波浪能还是水流的势能，均具有功率密度大、对生态环境破坏小的特点[2]。对发电装置的开发建设具有多层次的能源建设意义，既是对水资源的综合利用，又能较好地促进江河湖海的综合治理，具有重大的现实意义与长远价值[3-4]。

海水覆盖了地球中表面的71%，其中蕴涵的可利用能量大大超过目前全球能源需求总和[5]。水能的利用主要依靠流体机械将水的势能或动能转换为可供电力设备使用的电能。能源利用率主要由水的势能以及流体的流场情况决定。我国在水电技术上的自主研发能力仍有所欠缺，难以与发达国家相抗衡。自主研发力量的不足影响了我国水电行业的发展。

目前，我国水流发电装置主要存在以下不足。

①由于水流速度的无序变化，能量的捕捉和转换不可控，使得发电机无法在水速不稳定的区域稳定、持续发电。

②中小型水流发电设备中主要采用变速恒频技术。该技术会产生大量的谐波，对电网影响较大，影响发电的稳定性。

③现有装置整体安装于水下，安装、测试、维修难度较高，提高了发电成本。如何利用不稳定动力源实现恒频发电是发电技术的一大难题[6]。

针对现有技术的不足，利用马达恒速控制水流发电的方式，将水轮机转换而来的液压能转变为马达输出的稳定机械能，可保证发电机恒频、高质量发电。同时，采用压电阀代替传统两位三通阀控制变量马达排量，改善了传统三通阀控制周期长、响应速度慢、发热效率低等问题。这可以极大地提高系统的响应频率与控制精度，使变量马达的输出转速波动范围更小，从而提升系统在各种环境下的适应性；马达输出转速稳定在1 500 r/min左右，更好地实现了发电机的稳定发电。

1 压电式马达变量控制系统原理

液压稳频控制系统原理如图1所示。

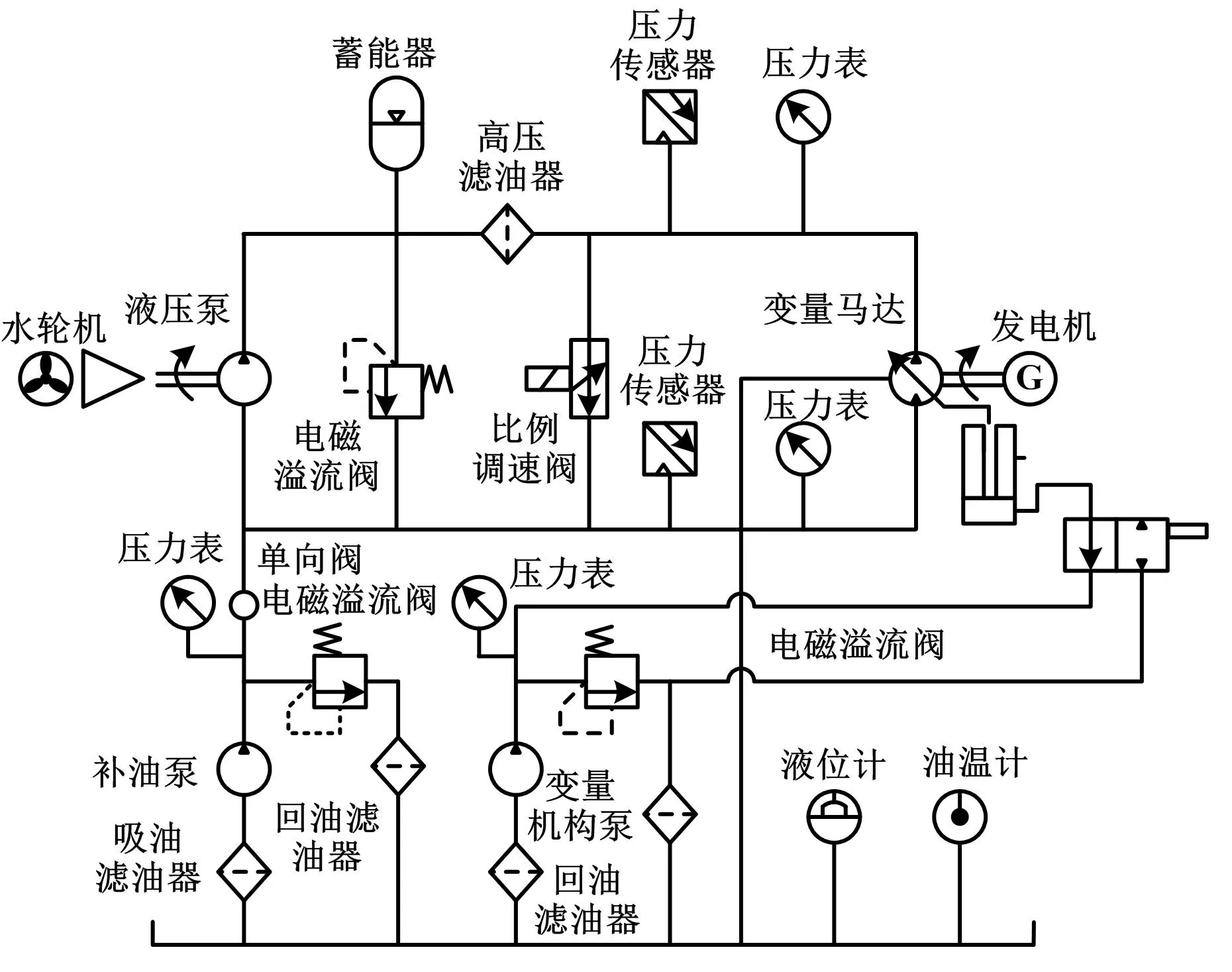
图1 液压稳频控制系统原理图Fig.1 Schematic diagram of hydraulic frequency stabilization control system

核心控制元件包括水轮机、液压泵、变量马达、比例调速阀等[7]。水轮机从水流中获取能量，经液压泵实现水流能-机械能-液压能的转换。此时的能量仍然是非稳定动力。在主路中，首先经马达变排量机构进行粗调，再经比例调速阀进行旁路调节以稳定马达转速，向发电机输出稳定动力。

压电式马达变量控制系统原理如图2所示。

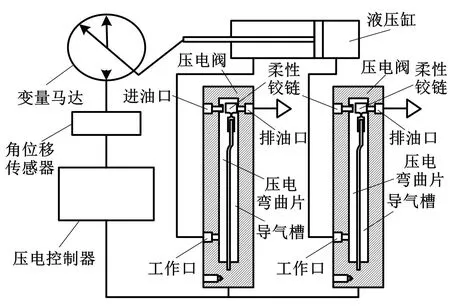
图2 压电式马达变量控制系统原理图Fig.2 Schematic diagram of piezoelectric motor variable control system

系统由两个压电阀、液压缸、变量马达、角位移传感器以及压电控制器组成。变量马达的斜盘由液压缸活塞杆控制。液压缸的两腔分别连有一个压电阀。压电阀内部对称放置呈悬臂状的压电弯曲片。压电弯曲片运动形式如图3所示。

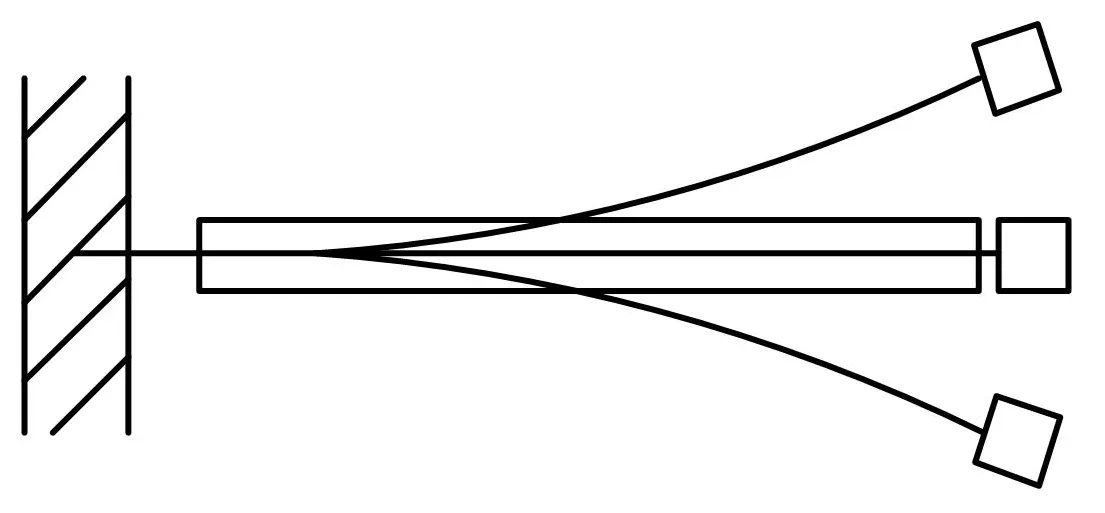
图3 压电弯曲片运动形式Fig.3 Piezoelectric bending plate motion form

系统控制原理如下。当需要调整变量马达排量时，压电控制器产生的交变电压传递至压电弯曲片。由于两个压电弯曲片对称放置，相同的电压使其端部产生相反的弯曲位移，使得两个压电阀可以分别打开进油口与排油口。此时，液压缸一腔进油而另一腔油液经与其相连的压电阀排油口排出，从而改变活塞杆位移调整变量马达斜盘角度。最后，经角位移传感器监测调整反馈至压电控制器调整输出电压，形成局部闭环控制系统。

在选择压电弯曲片型号时，通常需要考虑整体机构的机电转换特性与驱动特性，用数理方法计算压电弯曲片自由端的挠度、转角刚度等自由量。挠度的大小(即自由端位移量)是衡量压电弯曲片驱动特性的重要参数[8-9]。考虑到整个系统的布局组成，压电阀不宜占据过多空间。这要求压电弯曲片在满足挠度要求的前提下具备充足的输出力。基于此，本文采用PZT-5H种类下PZT-3-1.5型号叠层式压电弯曲片。PZT-3-1.5型压电弯曲片性能参数如下：尺寸为(68×20×1)mm3；驱动电压为0～±150 V；单向最大输出位移为1.5×(1±20%)mm；最大输出力为30×(1±20%)N；压电常数d31为-275×10-12m/V；弹性模量Ep为56×109N/m2;阻尼系数c为0.168。

2 压电式马达变量控制系统建模

变量马达型号为AV6-28。变量马达控制机构采用压电阀控制液压缸活塞杆位置的控制方法，通过阀体内压电弯曲片的弯曲运动控制进油口的启闭，进而驱动液压缸将需要改变的位移传送到变量马达的缸体上，以实现对变量马达排量的控制。整个系统可看作由压电阀控制系统与变量马达控制系统整合而成。因此，以下分别对两个系统进行分析。

根据马达变排量机构的特性，且由于马达的斜盘为一个大惯量部件，可将马达的变排量控制系统简化为一个一阶系统。变量马达油液泄漏时，变量马达的流量连续方程可取为：

(1)

式中：q为变量马达流量连续方程；Cm为变量马达的内泄漏系数；p1为液压高压管路压力；pt为液压低压管路压力；Cem为马达外泄漏系数；Dm为马达排量；wn为马达转速；V0为马达一个腔的容积；βe为流体弹性模量。

对式(1)两边进行拉式变换，可得：

(2)

式中：Cm1为马达总泄漏系数；Dm0为马达稳态排量；wm0为马达稳态转速。

变量马达的负载力矩平衡方程为：

(3)

式中：Jt为马达与马达轴负载的总惯量；B为流体黏性阻尼系数；T为外负载力矩。

对式(3)两边进行拉式变换，可得：

Dm0p1=JtsΩm+BΩm+T

(4)

由式(2)、式(4)可推出变量马达传递函数：

(5)

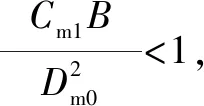
(6)

(7)

式中：wh为变量马达固有频率；ζh为变量马达阻尼比。

变量马达转速对其排量的传递函数为：

(8)

压电阀采用叠层式压电弯曲片驱动，片状压电陶瓷驱动器主要应用于对空间体积、位移以及受力性质有特殊要求的场合。早在1997年，国外学者Goldfarb和Celanovic便提出了同时包括动态特性与迟滞效应的压电迟滞模型。该模型也是目前较为常用的压电陶瓷机电模型[10]。将其与压电弯曲片弹簧-阻尼等效模型相结合，可建立如图4所示的悬臂式压电弯曲片简化动力学模型。

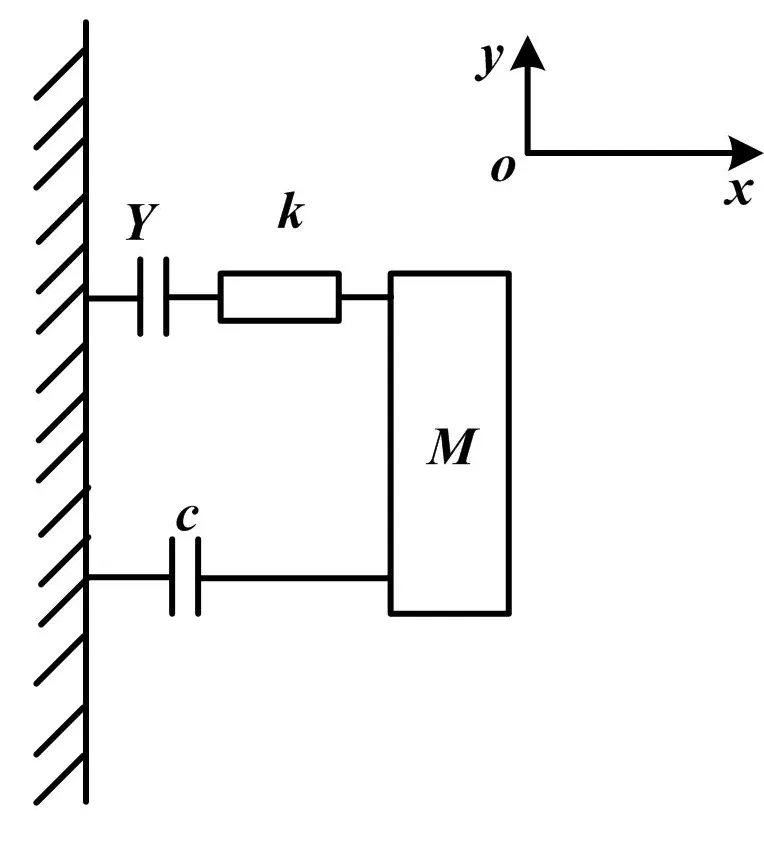
图4 悬臂式压电弯曲片简化动力学模型Fig.4 Simplified dynamic model of cantilever piezoelectric bending plate

图4中：M为质量块等效质量；k为压电弯曲片刚度；c为压电弯曲片阻尼比；Y为压电弯曲片自由端静挠度值；x为质量块受冲击的移动坐标。

压电弯曲片的刚度k由其自身结构以及自由端外力F所引起的自由端静挠度变化值决定[11]，为：

(9)

式中：L为压电弯曲片长度；w为压电弯曲片宽度；d为压电弯曲片厚度；Ep为压电弯曲片弹性模量。

根据动力学模型，可建立压电弯曲片的动力学方程：

(10)

(11)

由于系统精度与稳态误差成反比，在变量马达稳频系统中，存在的稳态误差是由输入信号与负载力矩引起的。而压电弯曲片作为压电阀的驱动元件，可执行1 nm量级的分辨率和1 000 Hz量级的宽带结题运动，并可提供数瓦级机械效率[12]。因此，在分析稳态误差对系统的影响时，只需考虑负载力矩以及控制电压对排量的影响即可。结合式(8)，此时变量马达稳频控制系统传递函数为：

(12)

式中：K为变排量系统增益；t为时间常数；U为变量马达机构的控制电压。

此时，压电式马达变量控制系统传递函数为：

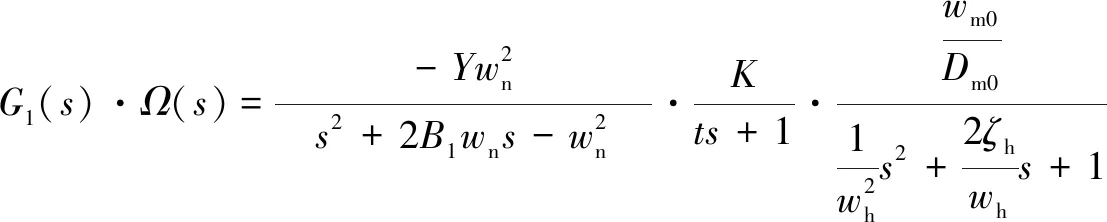
(13)

3 压电式马达变量控制系统分析

为了对比压电式控制系统与传统三通阀控制系统的性能差异：首先，仅针对所选马达的技术参数进行仿真分析代表传统三通阀控制系统；然后，加入压电阀的技术参数构成完整的压电式马达变量控制系统；最后，进行仿真分析。

通过查阅技术参数表可知：AV6-28型变量马达转动惯量Jm=1.7×10-3kg·m2;稳态排量Dm0=20 ml/r;负载的转动惯量为Jt=2.75×10-3kg·m2;马达一个腔的容积V0=84 ml;系统中的流体通常为液压油;流体弹性模量βe=6.987×108N/m3;ζh的取值范围为0.1～0.2。此处取0.2。将以上数据代入式(7)，可得wh=110 rad/s。通过Matlab软件，绘制如图5所示的传统系统的仿真伯德图。

图5 传统系统的仿真伯德图Fig.5 Bode diagram for traditional system simulation

从图5可以看出，传统的变量马达控制系统传递函数的阻尼系数小，系统震荡幅度较大，平稳性能较差。

压电弯曲片在交变电压的驱动于阀体内产生高频振动。为保证其振动状态的恒定，临界阻尼系数成为判断振动状态是否恒定的重要参数。

PZT-3-1.5型压电弯曲片由10层0.1 mm压电弯曲片烧结而成，临界阻尼系数为0.24。结合阻尼系数，可得阻尼比B1=0.7。根据式(9)与系统阻尼比计算式，可得k=3 N/mm、m=0.005 3 kg，并取压电弯曲片自由端静挠度值Y=1.5 mm。为了验证新系统的平稳性，将以上参数加入压电阀仿真，利用Matlab对系统模型进行仿真分析，得到如图6所示的压电式马达变量控制系统仿真伯德。

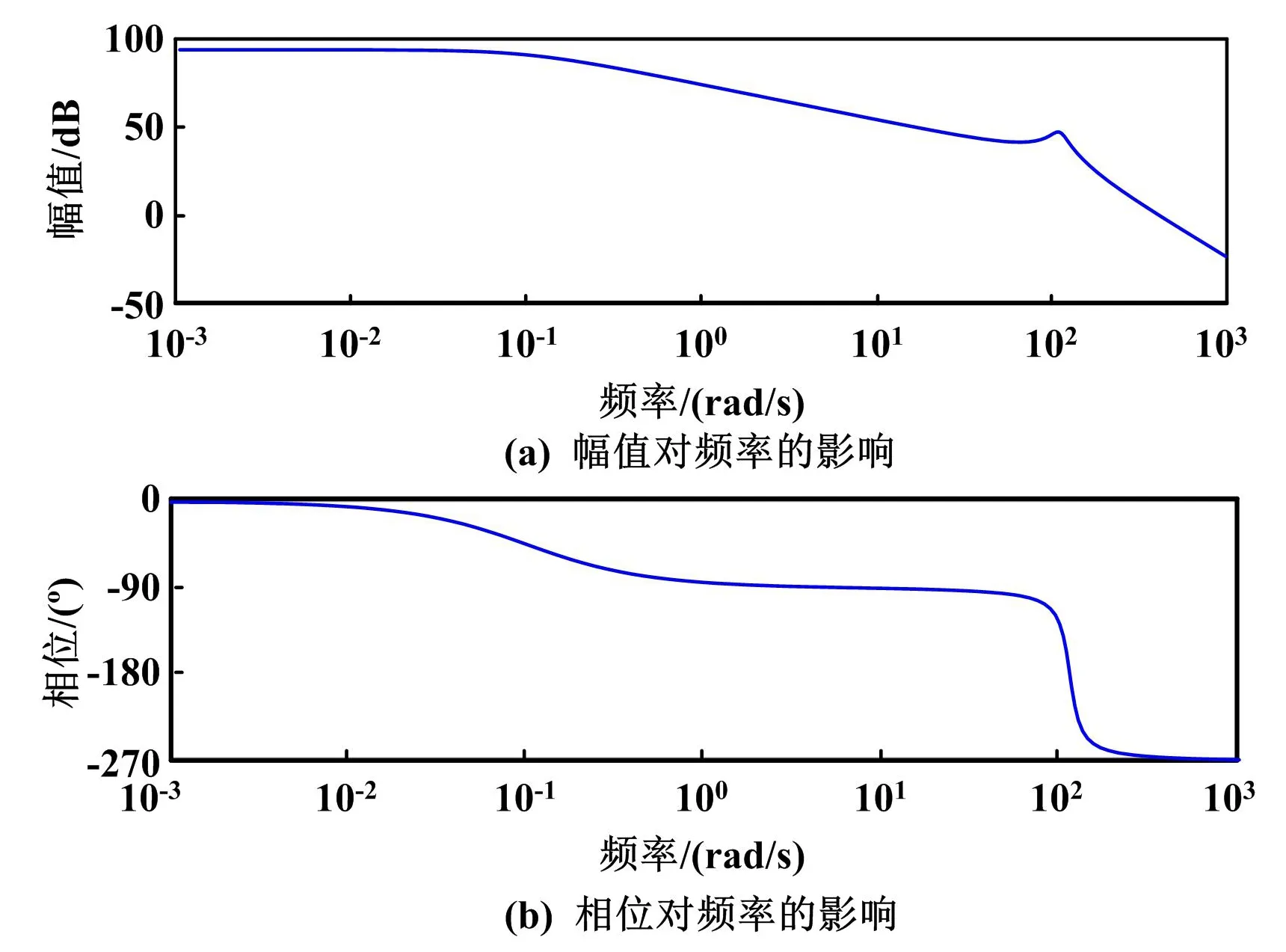
图6 压电式马达变量控制系统仿真伯德图Fig.6 Bode diagram for piezoelectric variable motor control system simulation

从图6可以看出，采用两种控制系统共同控制的变量系统超调量小，平稳性趋于缓和。因此，系统具有稳定的动态性能，相较于传统控制方式有更好的动态性能。压电元件具有更加优异的性能优势，在满足控制要求的情况下采用压电驱动要优于励磁线圈驱动。唯一需要注意的是阻尼比对于压电控制元件的影响。对于同样满足技术要求的不同压电控制元件，不同的阻尼比会使系统的超调量及调整时间发生相应的变化。

4 结论

本文基于现有水流发电装置的不足，提出采用压电阀控制变量马达排量的新型控制系统，进而减小变量马达转速波动范围。首先，对传统变量马达控制系统进行建模仿真得到传统控制系统的伯德图，随后将压电阀控制参数加入系统中得到压电式马达变量控制系统的伯德图。通过对比发现，在自然水流液压稳频发电系统中，虽然存在动力源不稳定且变化的无序性，但是从仿真结果来看，压电阀控制变量马达的系统能够很快地达到稳态，且超调量小。因此，系统表现出更好的适应性，适用于各种动力不确定的水流发电系统。本文也印证了将压电技术引入水流发电领域的正确性。