一种面向多物联代理在线应用的弹性资源调度算法
2022-03-23缪巍巍王传君李世豪张明轩
缪巍巍,王传君,曾 锃,李世豪,张 震,张明轩
(国网江苏省电力公司信息通信分公司, 南京 210024)
如今,新兴的计算密集型应用往往需要超过单一设备所能提供的计算资源,因此许多已有的系统[1-4]将计算密集型应用卸载到云端或者附近的高性能计算服务器来加快处理速度。比如,MCDNN[1]将基于深度神经网络的视频处理任务卸载到云端,Odessa[2]选择附近的高性能计算服务器作为额外的计算资源去从实时视频中识别对象,LEO[3]利用芯片数字信号处理器、GPU并协同云服务器来运行推断算法。尽管这些工作加快了处理速度并降低了时延,但在一些网络通信资源匮乏的场景中,云服务器和高性能计算服务器带来的丰富资源却不是总能轻易获得的。在电力物联网[5-6]场景下,不同的边缘物联代理产生类型和结构均不同的数据,运行不同的应用,并且组成应用的任务之间可能存在依赖关系,如何将这些任务调度到合适的物联管理平台[7-9]的数据处理模块来处理成为一个颇具挑战性的问题。
本文试图设计一个面向多边缘物联代理在线应用的调度框架。该框架无需通信基础设施的辅助,且数据处理应用是由多个存在依赖关系的任务构成的。在一个应用请求在边缘物联代理上被提出前,物联管理平台的数据处理模块上可能已有不少不同种类的计算密集型应用在占用计算资源、消耗能量,留给应用处理的资源是随着时间不断改变的,如何与其他已有应用更好地计算资源是值得考虑的。而在边缘物联代理能量有限的情况下,负载均衡的引入能使得整个系统中的能量得到更充分地利用,在这里,负载均衡定义为单个应用的处理给每个物联代理带来能量消耗占剩余能量比重的均衡程度。
在这样的情形下,在线对应用进行调度决策显然能够更好地适应复杂的资源环境。针对与已有应用共享资源的问题,在应用处理请求到来时,物联管理平台的数据处理模块可自定义应用允许占用计算资源的比重。此外,由于物联管理平台的数据处理模块可能在地域上是分布的,2个数据处理模块之间的数据传输速度较慢,连接可能也不稳定,因此多个应用同时在物联管理平台的某个数据处理模块上处理时容易因为争抢传输连接而彼此影响。这里采取一个保守的策略:在单个应用的调度决策中假设一个物联管理平台数据处理模块上同一时间至多只能存在2条连接,一条用于发送数据,一条用于接收数据;这样能减少多应用因争抢传输连接对彼此的影响,使得更多的应用顺利处理,增强了应用处理用时的可预测性,也更贴近客观实际。为解决问题提出了一个两阶段的启发式算法:每当一个应用处理请求在一个物联代理上被提出,首先以优化处理用时为目标进行一次初始调度,然后以实现负载均衡为目标进行多轮的调整调度。最后,进行了大量的仿真实验,充分验证了所设计算法能够在较短的时间内达到接近最优的表现。
1 相关工作
由存在依赖关系的任务构成的应用(将任务视作定点,依赖关系视作有向边,从而构成有向无环图,因此本文简称为DAG式应用)在多个处理器上的调度,已有不少研究[10-12]。比如,SUNDAR等[10]研究了单个DAG式应用在一个一般的云计算系统上的卸载调度。这个云计算系统包含一个远程云服务器和一个异构的本地处理器网络。文中描述了一个在不违背应用处理时限要求下的最小化能量开销的优化问题,并提出了一个启发式算法ITAGS来获得一个有效的决策。ITAGS首先为应用的每个任务分配了一个任务处理时限,然后基于这个任务处理时限对每个任务的调度进行优化。ITAGS并不适合本文的场景,因为文献[10]作了2个隐含假设,一个是应用任务分配到设备上后,独占设备所有计算资源,这在真实场景中并不现实;另一个是在应用处理过程中,设备之间能以给定的速度稳定地通信。尽管文献[10]研究的只是单个DAG式应用的调度,但在实际处理中,设备之间的通信速度必然不可能非常稳定。而当应用处理系统中有多个应用同时在进行处理时,无线传输资源的有限会导致应用之间因为争抢传输连接而相互影响,传输速度更加难以预测。
F-MStorm[13]是一个基于反馈的在线分布式移动流处理系统。与当前主流的移动流处理系统MStorm[14]采用静态的配置和调度不同,它根据流处理过程中来自各个移动设备的反馈,在配置层面动态调整每个移动设备上的处理器数目,在调度层面动态调整任务分配方案,在执行层面动态调整上游任务对下游任务的结果数据分配。从而系统可以快速适应变化的环境,始终保持高效的表现。虽然文献[13]的应用场景和本文非常相似,但它关注的是流处理,和本文的DAG式应用处理不同。
文献[15]关注的是DAG式应用在边缘集群上的调度,并以优化应用处理时长和能量开销为目标提出了2种基于任务复制的启发式算法。文献[15]假设处理器是同构的,且未将负载均衡考虑在内。
与文献[15]类似,LIU等[16]同样研究DAG式应用在边缘服务器上的调度,并针对优化应用处理时长这个目标,提出了一种具有性能保证的近似算法。但是文献[16]中的应用必须部署到有对应处理功能的边缘服务器上。除此以外,由于它没有将能量考虑进系统,因此相应地也没有考虑负载均衡。
2 问题描述
2.1 应用模型
在应用模型中,每个电力物联网应用有一个软性的完成时刻限制Tmax,也就是说应用并非要严格在Tmax前完成,但超过这个时刻完成会受到惩罚,比如在电力调度应用中,希望调度尽可能快地完成,但并没有一个严格的时间限制,因此使用惩罚函数的形式是比较合理的。定义惩罚函数:
F(T)=max{0,T-Tmax}
(1)
式中:T是应用实际完成的时刻。一个应用中的任务之间的依赖关系可以用一个有向无环图来刻画,其中每个结点Xi表示一个任务i,它的计算量用Wi来表示,每条有向边(Xi,Xj)表示任务Xi需要传输结果给任务Xj,数据规模为di,j,因此Xj的计算依赖于Xi的计算结果。
图1(a)展示了一个应用的任务图。在一个给定的任务图中,称没有父亲结点的任务为入口任务(即图中的X1),没有孩子结点的任务为出口任务(即图中的X5和X6)。为方便起见,对于一个给定的DAG任务图,首先对其标准化。
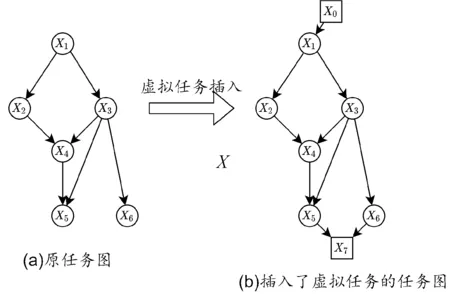
图1 任务图和标准化
插入2个计算量为0(即W=0)的虚拟任务。一个任务插在开头代表应用请求的提出,由它引出有向边指向原DAG任务图中所有的入口任务,并且有向边上需要传输的数据规模为0。另一个任务则插在结尾用来汇总所有的结果数据,由原DAG图中所有的出口任务引出有向边指向它,有向边上传输的数据就是需要汇总的结果数据。显然,这2个任务实际分别成了新任务图唯一的入口任务和出口任务,在调度中,应用可能规定了入口任务和出口任务必须分配到的模块。用nentry来表示入口任务的编号,用nexit来表示出口任务的编号。显然这样的处理不失一般性,因为它并没有改变应用原有的结构。图1(b)展示了对图1(a)中的任务图进行标准化的结果,X0和X7是被插入的2个虚拟任务。
假设一个应用的任务总数为M(M≥3),其中包含2个虚拟任务。任务编号为0,1,2,…,(M-1)。
2.2 资源模型
考虑一个物联管理平台有多个数据处理模块构成,这些模块可能有不同的处理速度,每个模块在同一时间只能处理一个任务,与此同时,其他分配到这个模块上的任务在处理队列中等待。
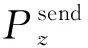
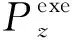
2.3 计算模型
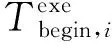
(2)
用d(i)来表示任务Xi所在数据处理模块的编号,
d(i)∈{0,1,2,…,(N-1)}
(3)
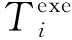
(4)
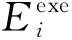
(5)
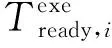
(6)
显然,入口任务Xnentry准备好计算的时刻就是应用处理请求被提出的时刻,也就是:
(7)
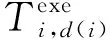
(8)
(9)
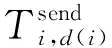
(10)
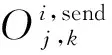
(11)
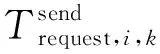
(12)
(13)
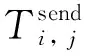
(14)
其中,
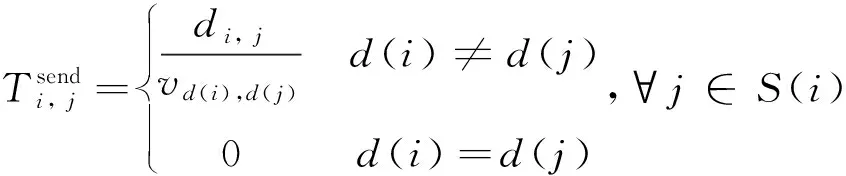
(15)
此外,任务Xi向它的直接后继任务传输结果数据总的开始和完成时间与它具体向其中每个直接后继任务传输结果数据的开始和完成时间有如下关系:
(16)
(17)
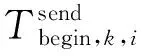
(18)
(19)
式(18)是显然的,式(19)表明如果Xi的另一个直接前驱Xl在Xk之前请求向Xi传输结果数据,那么Xk就必须等到Xl完成这次传输后才能有机会开始传输。
不难算出在应用处理在数据处理模块z上的能量消耗Ez:计算消耗的能量,发送数据消耗的能量,和接收数据消耗的能量。用T(z)表示分配在模块z上的任务编号组成的集合,那么,
(20)
应用处理带给模块z的能量消耗Ez占剩余能量的比例为
(21)
并且
ηz≤1
(22)
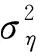
(23)
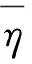
(24)
最后,应用的完成时刻
(25)
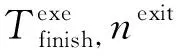
2.4 问题描述
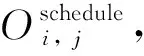
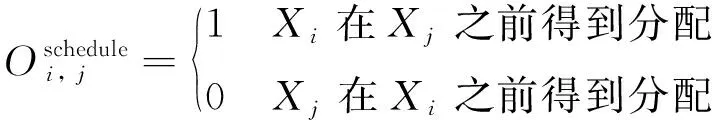
(26)
基于这个定义,为了保证应用的顺利处理,如果有2个任务被分配到了同一个模块上,并且它们之间存在依赖关系,那么被依赖方应当在依赖方之前得到调度,即,
(27)
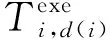
(28)
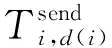
(29)
也就是说,模块d(i)必须等到本应用所有在任务Xi之前就分配到它上面的任务完成结果数据的传输时,才能开始传输任务Xi的结果数据。
至此,可以总结该问题:在电力物联网场景下,由多个物联代理生成存在依赖关系的任务构成一个DAG式应用;每当一个应用处理请求被提出,我们要根据请求的完成时刻软性限制、每个模块允许用来处理该应用的CPU资源占比,每个模块的剩余能量、发送/处理速度、功率等信息,以及应用的结构和其他相关信息,在线确定如下未知量:
1) 任务调度顺序:
2) 任务分配决策:
d(i),i∈{0,1,2,…,(M-1)}
其中,入口任务和出口任务必须被分配在给定的模块上,也就是
d(nentry)=zsubmit
(30)
d(nexit)=zsubmit
(31)
3) 任务向直接后继任务发送结果数据的顺序:
∀j,k∈S(i),j≠k
来最小化目标变量
式中:α和β是比例因子,用来调整“满足完成时刻限制”和“负载均衡”对优化目标的重要性。通过合理的设置比例因子,能够实现两者的权衡。
总的来说,这个问题可以被描述成一个整数规划问题:
通过灵活地设置比例因子α和β的值,对这个问题的解决方案可以在各种情况下发挥作用。例如,当应用是时延敏感型或无能量约束情况下,可以将α/β调得较大,以强调目标变量中“满足规定完成时刻限制”的重要性。
3 算法设计
从问题描述中,不难发现,要在线确定2个顺序:任务调度顺序和任务向直接后继发送结果数据的顺序,以及一个分配:任务分配,来优化一个包含“任务完成时刻”和“负载均衡”2个要素的目标函数。如果要以穷举所有情形的方式来搜索最优解,仅仅任务分配就是O(NM)级别的,这在应用包含任务数多、模块数多的情况下,是难以接受的。因此,提出一种两阶段启发式算法:当一个应用处理请求被提出,首先以优化处理用时为目标进行一次初始调度,然后以实现负载均衡为目标进行多轮调整调度。
3.1 初始调度阶段
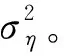
3.1.1决定任务调度顺序和任务发送结果数据的顺序
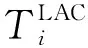
(32)
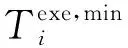
(33)
TLAS显然能反映一个任务的紧急程度,在算法中,使用任务的TLAS作为任务调度的优先级度量,TLAS越小,优先级越高。
具体计算每个任务TLAC和TLAS的方法如下:假设任务Xi所有直接后继任务的TLAC和TLAS全部已经计算完成。在任务Xi向它的直接后继任务传输结果数据时,直接后继任务的TLAS是直接后继任务最晚允许开始计算的时刻,反映了直接后继任务对于来自Xi的结果数据的渴求程度。特别是考虑到实际情况中,来自一个任务的结果数据往往规模相似,与一个模块建立的连接速度往往大小相当,传输时间对决定传输顺序的影响并不是很大。因此根据直接后继任务的TLAS的大小来确定传输顺序可能是一种比较快捷而稳妥的选择,将任务Xi的直接后继任务根据TLAS从小到大排序,这个顺序就是算法决定的任务Xi向直接后继任务传输结果数据的顺序。
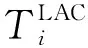
(34)
将这|S(i)|个二元组按照传输顺序(也就是TLAS从小到大的顺序)排列,得到如下序列:
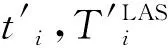
(35)
(36)

按照上面给出的方法算出所有任务的TLAS,从小到大排列,对应的任务顺序就是算法给出的任务调度顺序。根据上面对于TLAS的计算方法,可以看出,这样的一个排序是任务关于依赖关系的一个拓扑排序,也就是说,如果按照这个顺序调度任务,每个任务必然在它的直接后继任务之前得到调度。
3.1.2任务分配
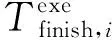
算法1初始调度阶段算法
输入:应用任务图G,模块相关信息,应用请求提出的时刻Tsubmit和模块zsubmit。
输出:任务分配方案。
a) 计算G中任务的逆拓扑排序S
b) 按S依次计算G中每个任务的TLAS
c) ForG中的每个任务
d) 按直接后继任务的升序传输结果数据
e) 优先级队列PQ←所有任务根据TLAS的升序排序结果
f) 从PQ中按序取出每个任务Xi,依次进行g)~j)的操作
g)If是入口或出口任务 Then
h)d(i)←zsubmit
i) Else
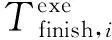
3.2 调整调度阶段
在这一阶段,任务被重新分配来实现负载均衡,但是并不改变任务的调度顺序和任务向直接后继任务传输结果数据的顺序。调整调度阶段分若干轮,在每一轮按照下述方式来调整。
根据当前的分配策略计算出应用带给每个模块能量消耗占模块剩余能量的比重η,按照η值由大到小的顺序,逐个考虑模块上的当前分配任务的重新分配。重新分配k个模块上的任务,对这些任务逐个尝试重新分配到其他模块上来减小目标变量的取值,具体而言,重新分配到使得目标变量取值降低最多的模块上,如果重新分配无法降低目标变量取值,就放弃这次尝试。这里不考虑入口任务和出口任务的重新分配。假设分配在η值前k大的模块上的任务总共有s个,那么一轮共尝试约s(N-1)次重新分配。不断重复每一轮的调整调度,直到连续若干轮目标值的优化幅度都很小。k值的选取和模块数N有关,较大的N应当对应较大的k。选取k=[N/3],这样每一轮调整的尝试次数比较合理,既不会太多,并且在一定轮数内就能达到不错的优化效果。
算法2调整调度阶段算法
输入:算法1得到任务分配方案,预先设定的k值。
输出:调整完的任务分配方案。
a)O←所有模块根据η的降序排序结果
b) 对O中的前k个模块,依次进行c)~e)的操作
c) For 模块上的每个任务Xi
d) IfXi不是入口或出口任务Then
e)d(i)←使得目标值降低最多的模块
f) 重复步骤b)~e),直到连续若干轮优化幅度都很小
3.3 算法分析
穷举算法虽然可以得到理论上的最优调度决策,但是在应用包含任务数和模块数较大的情况下对应的高昂开销是无法接受的。这个两阶段的启发式算法能够在多项式时间内获取一个较好的调度决策,可行性高。下面简要分析一下这个启发式算法的时间复杂度:
在初始调度阶段,首先要计算每一个任务的TLAS,其中涉及对直接后继任务根据TLAS进行排序,时间复杂度是O(MlogM),总共有M个任务,因此总的时间复杂度是O(M2logM)。然后要对所有任务根据TLAS进行排序,时间复杂度是O(MlogM)。这时,分配每一个任务的时间复杂度是O(MN),总的时间复杂度是O(M2N)。综合来看,初始调度阶段的时间复杂度是O(M2(logM+N))。
在调整调度阶段,对于每一轮调整,首先要对所有模块根据η值进行排序,时间复杂度是O(NlogN),然后考虑重新分配任务,次数是O(MN),每一次重新分配需要计算一次目标值,时间复杂度是O(M2+N),因此每一轮调整调度的时间复杂度是O(M3N+MN2)。将以上分析结合起来,这个启发式算法的时间复杂度是O(M3N+MN2)。
4 实验
通过大量的仿真实验来评估所提算法的性能。使用随机生成的任务图和实际的参数值来作为实验数据,在一台搭载了i9-9880H CPU、16GB内存的笔记本上进行仿真。其中任务图的随机性体现在:结构随机,每个子任务计算量随机,子任务间传输结果数据规模随机。表1中列出了数据处理模块的参数,表2中列出了随机任务图的参数。

表1 数据处理模块参数

表2 随机任务图参数
首先通过在一个随机生成的任务图以及其他给定的参数上测试穷举算法的表现,来展示通过调整比例因子α和β的比值,本文提出的优化目标,能够在对“满足规定完成时刻限制”和“负载均衡”重要性的不同期望下,均给出合理的调度结果。然后,通过调整比例因子α和β的比值、模块情况、任务图规模,分别计算穷举算法、不包含调整调度阶段的启发式算法和完整版本的启发式算法对应的优化目标值,来展示在不同的情况下,启发式算法的各个阶段均发挥了期望的作用,在优化目标变量上均能给出接近穷举算法的表现。
仿真参数根据调查和经验设定,可能与实际情况有一些偏差,但对目标验证的影响程度并不是很大。比如在数据处理模块参数(表1)中,尽管电池容量设定得非常小,但是由于考察的是耗能量占剩余能量比重的负载均衡,这样的设定不但不会影响结果的准确程度,反而使得结果更为直观。
4.1 优化目标的合理性
随机生成一个任务数M=12的任务图,并设置模块数N=4。假设应用处理请求在t=0.2 s时刻被提出,其入口和出口任务需要在模块0上完成,此时每个设备的剩余能量占比和允许应用使用的CPU资源占比见表3。

表3 应用处理请求提出时的一些额外参数(N=4)
首先设置一个比较宽松的完成时刻限制Tmax=3.5s,并让α=1,β从1变化到100。仿真结果表明,穷举算法得到的调度方案对应的完成时刻、各个模块上的应用处理耗能量占剩余能量比重、负载均衡因子如表4所示。
由此可以发现,在完成时刻限制比较宽松的情况下,通过优化本文提出的目标,几乎总能得到一个在应用处理完成时刻不超过Tmax情况下的将负载均衡做到最好的调度方案。
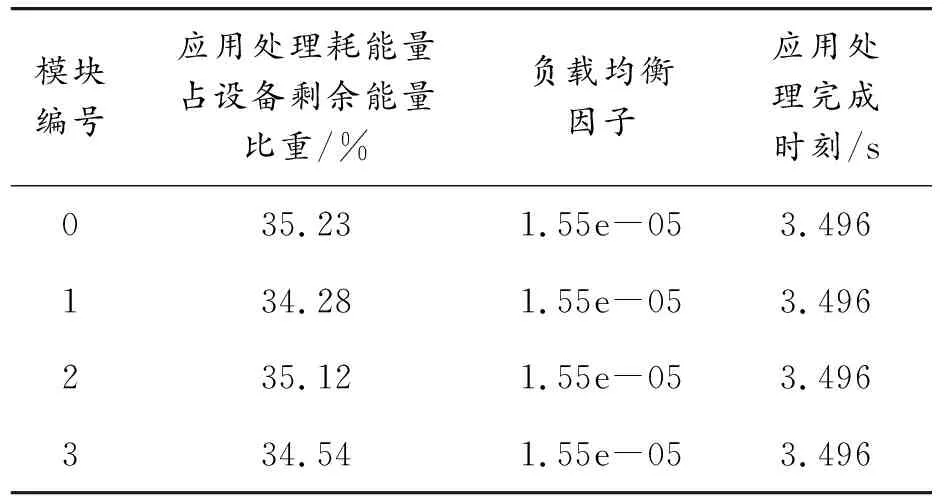
表4 Tmax=3.5 s时,不同α/β取值下的仿真结果
再设置一个比较紧迫的完成时刻限制Tmax=2.5 s,并令α=1,β取从1到50的一系列值,仿真结果如表5所示。
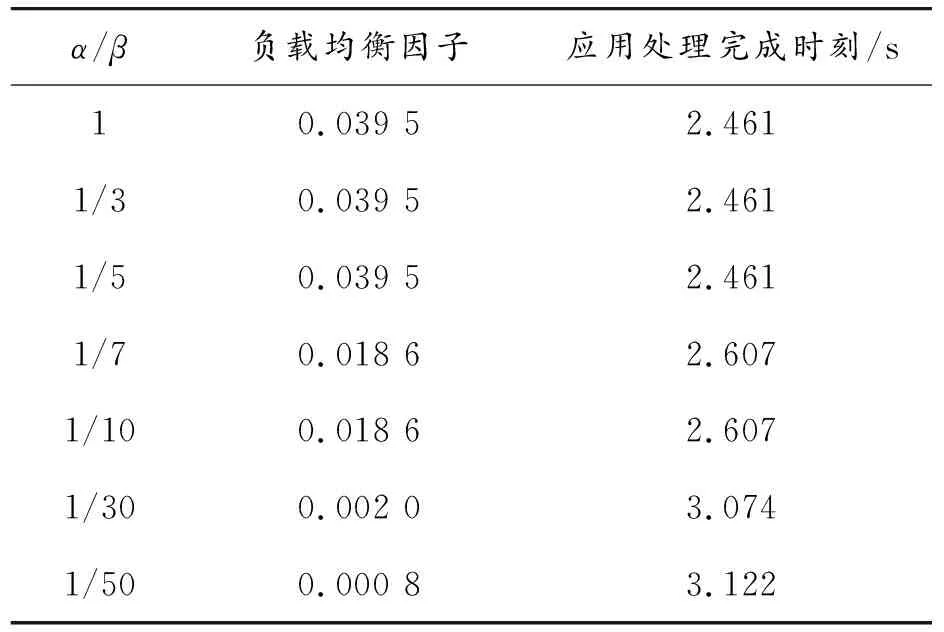
表5 Tmax=2.5 s时,不同α/β取值下的仿真结果
从结果中可以发现,在完成时刻限制比较紧迫的情况下,当β值比较小时,优化目标中“满足规定完成时刻限制”的重要性比较大,因此得到的调度方案是一个在应用处理完成时刻不超过Tmax情况下的将负载均衡做到最好的调度方案。随着β值逐渐增大,“负载均衡”在优化目标中的地位不断提高,得到的调度方案中的应用完成时刻开始突破Tmax,负载均衡也随之改善。
以上结果显示,通过合理调整比例因子α和β的比值,本文提出的优化目标,能够在对“满足规定完成时刻限制”和“负载均衡”重要性的不同期望下,均给出合理的调度结果。
4.2 算法性能
对于一组给定的模块信息、任务规模M、任务完成时限Tmax、α和β的比值数据,根据任务规模M随机生成10个不同的任务图,分别得到优化目标值后计算它们的平均值。
假设应用处理请求在t=0.2 s时刻被提出,其入口和出口任务需要在模块0上完成。N=4时每个设备的剩余能量占比和允许应用使用的CPU资源占比见表3;N=5时每个设备的剩余能量占比和允许应用使用的CPU资源占比见表6。
穷举算法、不包含调整调度阶段的启发式算法和完整启发式算法对应的仿真结果如表7~10所示。
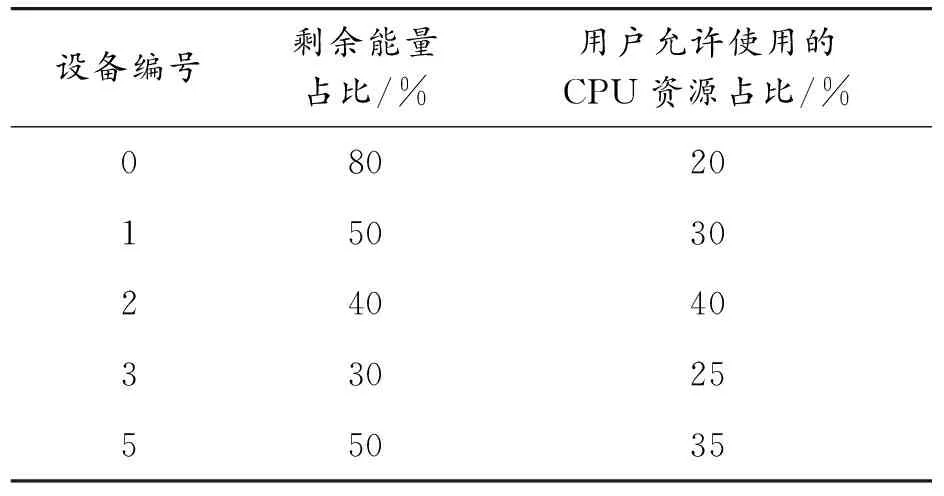
表6 应用处理请求提出时的一些额外参数(N=5)
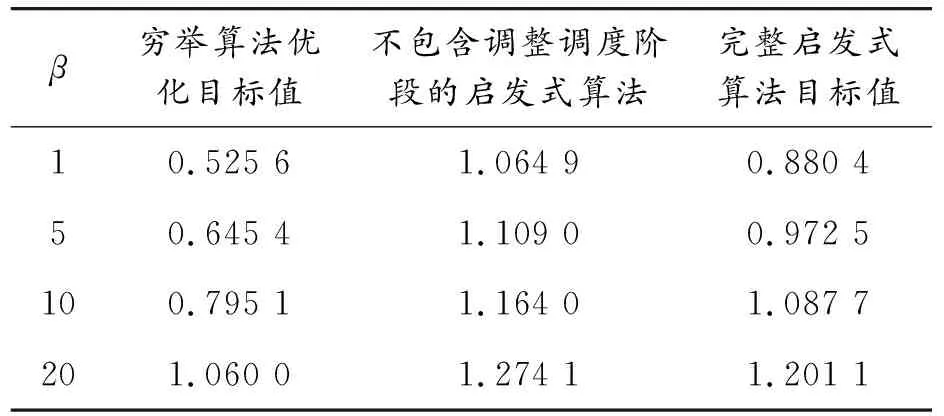
表7 M=7,N=4,α=1,Tmax=1.3 s时的仿真结果
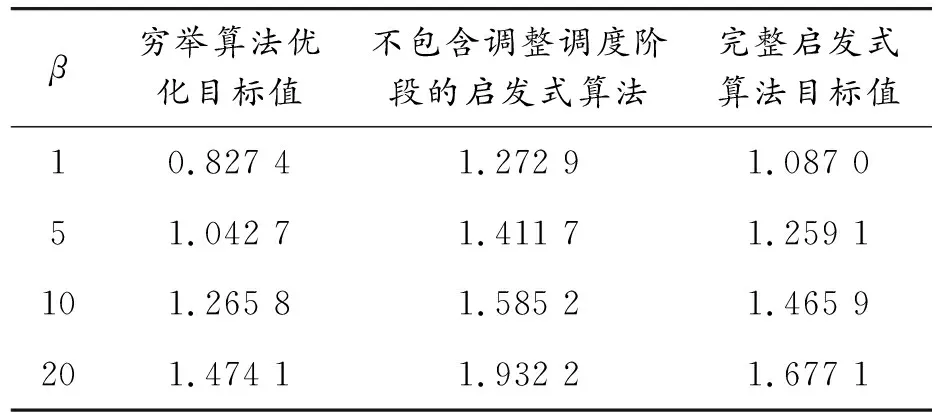
表8 M=9,N=5,α=1,Tmax=1.5 s时的仿真结果
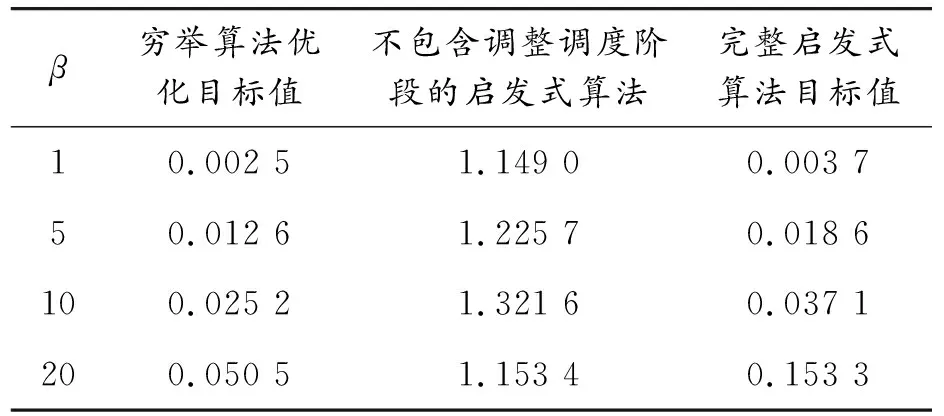
表9 M=12,N=4,α=1,Tmax=2.5 s时的仿真结果
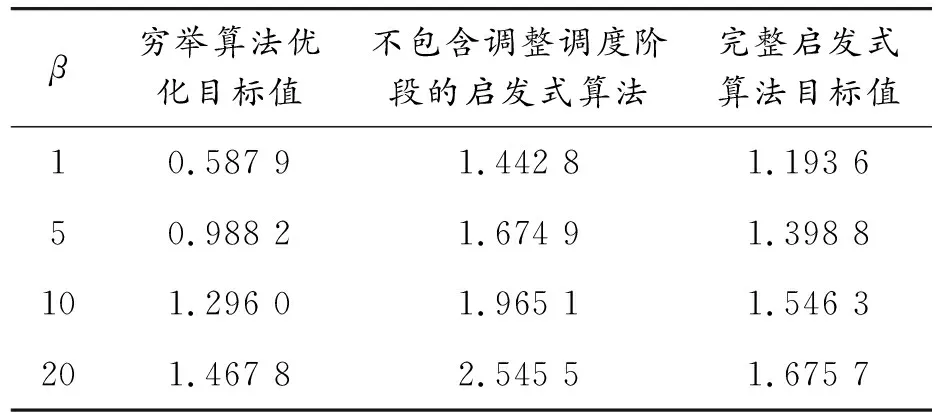
表10 M=13,N=5,α=1,Tmax=2.5 s时的仿真结果
以上仿真结果说明,启发式算法在性能上的表现与穷举算法是比较接近的,多数情形下,这两种算法之间的差距在10%~35%。不包含调整调度阶段的启发式算法在增加了调整调度阶段后,算法性能也有显著提升。在实验过程中发现,当M=13,N=5时,穷举算法在实验计算机上耗时已达到50 s,继续增大N=4和任务图的规模,耗时呈指数级别增长,而启发式算法的耗时则一直控制在0.001 s以内。
5 结论
提出了一个兼顾应用完成时间和负载均衡的联合优化问题,设计了一个两阶段的启发式算法。仿真实验结果表明:该算法能够在较短的时间内达到接近最优。
