芒稻河特大桥面板混凝土施工期裂缝与温度应力关系规律研究
2022-03-23黄兰可
黄兰可
(苏交科集团股份有限公司,南京 210019)
桥梁面板是承受过往车辆、行人荷载的直接承重结构,其结构的可靠性和耐久性直接影响到桥梁的承载能力与结构性能。据统计,约有97.2%的桥梁面板采用混凝土结构,由于混凝土施工期容易因局部温度应力张拉出现裂缝,导致混凝土表面出现剪切塑性破坏。由此可见,从根本上减小桥梁面板混凝土裂缝,必须了解桥梁面板混凝土施工过程中温度应力发展过程、分布规律,从而针对性地提出解决措施[1-5]。
针对桥梁面板裂缝控制,国内外学者做了诸多研究[6-8],取得了一定的研究进展。英国伯明翰大学的L.Poster教授对英国西部三郡的桥梁面板裂缝位置及温度应力分布做了大量研究分析,经过统计整理提出混凝土裂缝一般发生在温度应力的极值区域;加拿大桥梁结构与荷载研究院的I.Oscar教授基于弹性力学、数值方程的基础学科理论,将数值仿真技术应用到桥梁应力应变过程研究中,并建立了日本北海道雪川大桥的三维数值模型;我国大连理工大学的杜成斌教授对桥梁面板混凝土施工期温度场和温度应力计算分析进行了大量研究,对施工期水化热温度场和温度应力做了详细研究。
在此基础上,本文以五峰山过江通道跨芒稻河特大桥为研究实例,通过实例工程施工过程中温度、应力应变、裂缝大小等特征因子原型观测和分析对比,探讨施工期裂缝与温度应力关系规律。
1 工程概况
五峰山过江通道在K6+846.280~K8+821.680通过芒稻河特大桥跨越芒稻河。芒稻河大桥平面位于直线段上,最大纵坡坡度为2.5%,最短坡长为475 m,竖曲线最小半径:凸型20 000 m、凹型12 000 m。
全桥共12联,主桥上部结构采用(77+3×130+82) m预应力混凝土刚构-连续梁组合体系;引桥第1~7及11联、12联上部结构采用装配式部分预应力混凝土连续箱梁,芒稻河大桥桥跨布置图如图1所示。
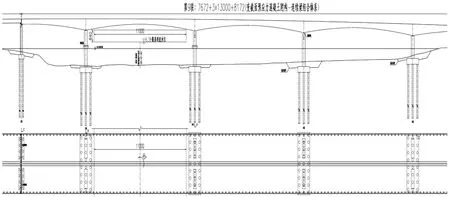
图1 芒稻河大桥桥跨布置图
2 混凝土施工期温度、应变监测设置
2.1 温度、应力应变监测点布置设计
为研究施工过程中混凝土面板区域温度、应力应变的变化过程,根据桥梁面板层厚度,共布置上、中、下3层监测点。其中上层与下层布设24个测点,中间层布设20个测点。在每个测点上布设一个温度测量计以及2个应力应变计,个别测点由于安装困难只设置1个应力应变计,因此总共布设68个温度测量计以及113个应力应变计,测量布置如图2所示。
2.2 温度、应力应变监测频次设计
混凝土初期应变及内部温度变化很剧烈,内部温度的升高主要来自于水泥水化热,水化热放热的高峰期出现在混凝土浇注后的2~4 d,混凝土内部的变形影响因素较多,初期变化也较大。因此要适当增加早期的应变监测频次,混凝土入仓前进行第一次数据(即初始数据)采集,第1~4 d每6 h测一次,第5~14 d每12 h测一次,第15~28 d每24 h测一次,并根据实际情况适当调整监测频次。
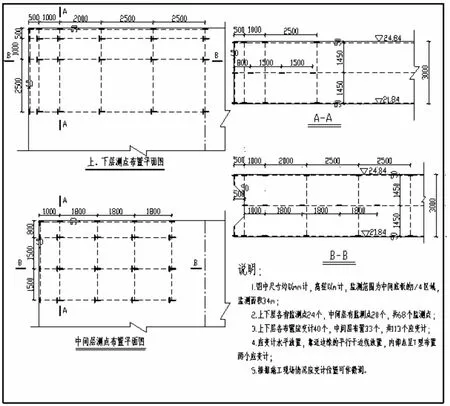
图2 桥梁面板各层监测点布置示意图
现场监测不同于实验室,由于存在各种不确定性的外界因素导致监测工作不能按期进行,例如:下雨等恶劣的天气原因以及现场施工情况造成的逾期监测。
2.3 桥梁面板混凝土裂缝发展过程监测与测量
参考以往研究经验,主要采用TTO-F20115裂缝宽度测量仪进行裂缝测量,同时在测量过程中采用钢卷尺辅助进行测量。用TTO-F20115裂缝宽度测量仪采用先进的粒子成像技术,可以同比例地模仿裂缝几何尺寸及发展过程,且测量精度较高,可以较好地研究裂缝发展规模及具体参数。
3 桥梁面板混凝土施工期监测结果及分析
3.1 混凝土热力学参数检测结果
不同龄期时的抗拉弹性模量及抗拉强度,体积收缩系数是混凝土热力学的主要参数指标。根据实例工程的检测记录,桥梁面板混凝土热力学参数检测数据如表1所示。
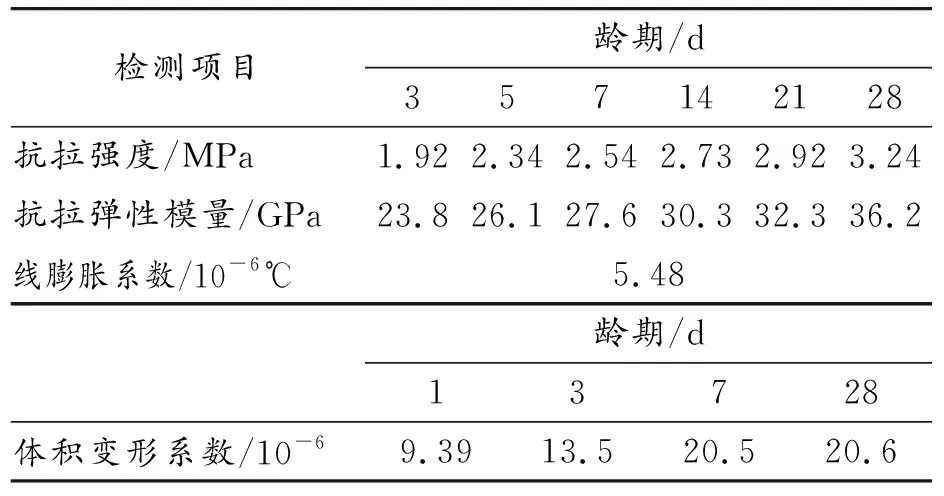
表1 桥梁面板混凝土热力学参数检测数据
3.2 典型监测点温度、应变历程分析
分析68个测点的数据应变过程,发现上、中、下3层的数据变化趋势基本一致,其中上、下2层的变化幅度要大于中层。因此,选择上层的第11个测点(编号111)为代表,其温度、应变历程见图3,图中111X、111Y分别为X方向、Y方向拉应变时程曲线,111T为温度时程曲线。
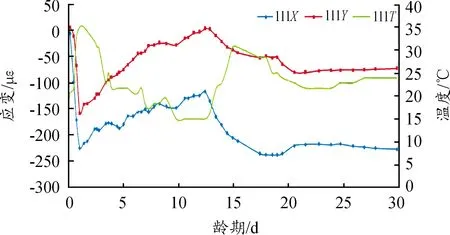
图3 上、下层典型监测点应变、温度时程曲线
分析可知:温度、应变可分为4个典型阶段:
1) 迅速放热、混凝土膨胀阶段(入仓后0~24 h)
桥梁面板混凝土刚入仓后,混凝土产生大量的水化热,在24 h内,温度迅速由19.0 ℃上升至35.2 ℃,温度平均增幅为0.675 ℃/h,此时X、Y方向的应变均迅速膨胀,其中X方向应变由0με增大至-150.3με(负号表示方向,下同);Y方向应变由5.1με增大至- 223.5με,增加幅度较大,幅度变化较快。
2) 放热减缓,混凝土膨胀速度减缓(入仓后1~13.5 d)
随着混凝土水化热逐渐减小,混凝土逐渐稳定。同时,由于仓内混凝土温度达到峰值,仓内混凝土向仓外热传递能量大于水化热能量,温度升温减缓并逐渐开始反弹下降,但下降幅度较缓慢。在12.5 d时间内,温度由35.3 ℃逐渐减小至14.5 ℃,平均减小速度为1.664 ℃/d,在减小过程中有数次波动反弹。与此同时,X方向应变与Y方向应变缓慢回升,至13.5 d时,X方向应变已恢复至入仓时刻的0με,而Y方向应变只恢复至-135.8με附近。在13.5 d时,混凝土由压应力开始变为拉应力。
3) 二次温升,混凝土缓慢收缩阶段(13.5~18 d)
在该阶段,其他部位混凝土浇筑,将部分水化热量传递至桥梁面板混凝土,仓内混凝土温度再次升高,导致温度再次上升,应变相应减小。
4) 最终温度,缓慢调整(18~30 d)
在该阶段仓内混凝土逐渐与仓外温度相同,温度基本稳定,X、Y方向应变也最终平衡稳定。
同时,选择上下2层多个监测点,监测点应力时程曲线如图4所示,数值为正表示压应力,数值为负表示拉应力。分析可知:在混凝土上、下2层,应力随时间变化规律一致,龄期0~2 d应力值下降,表现为受压状态,各点在2 d处极值的变化范围较宽。2 d之后,随着龄期增长,各位置应力值缓慢增长,但在28 d龄期之内,仍然表现为受压状态。
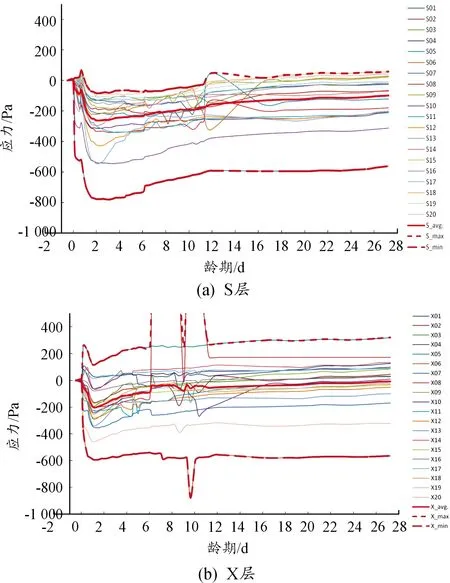
图4 上、下层典型监测点应力时程曲线
3.3 三维应变场切片云图分析
根据实际监测数据,以混凝土入仓后0.5、1、4.8、13、24.8 d为代表,各时刻的应变场切片云图见图5~9所示。其中,红色为正,表示拉应变;蓝色为负,表示压应变。
根据图5~9可知,在混凝土刚入仓时,桥梁面板混凝土X、Y方向应变均呈现中层中心部分受压周边区域受拉的特性,随着入仓时间推移,中心受压程度增大,范围也逐渐扩散。从第4.8 d开始,中心受压程度逐渐减小,受压范围也不断压缩。在13 d时,桥梁面板混凝土中心区域由拉应力转变为压应力,四周则呈拉应力状态,该状态在13 d后变化速率下降,至24.8 d时基本趋于稳定。
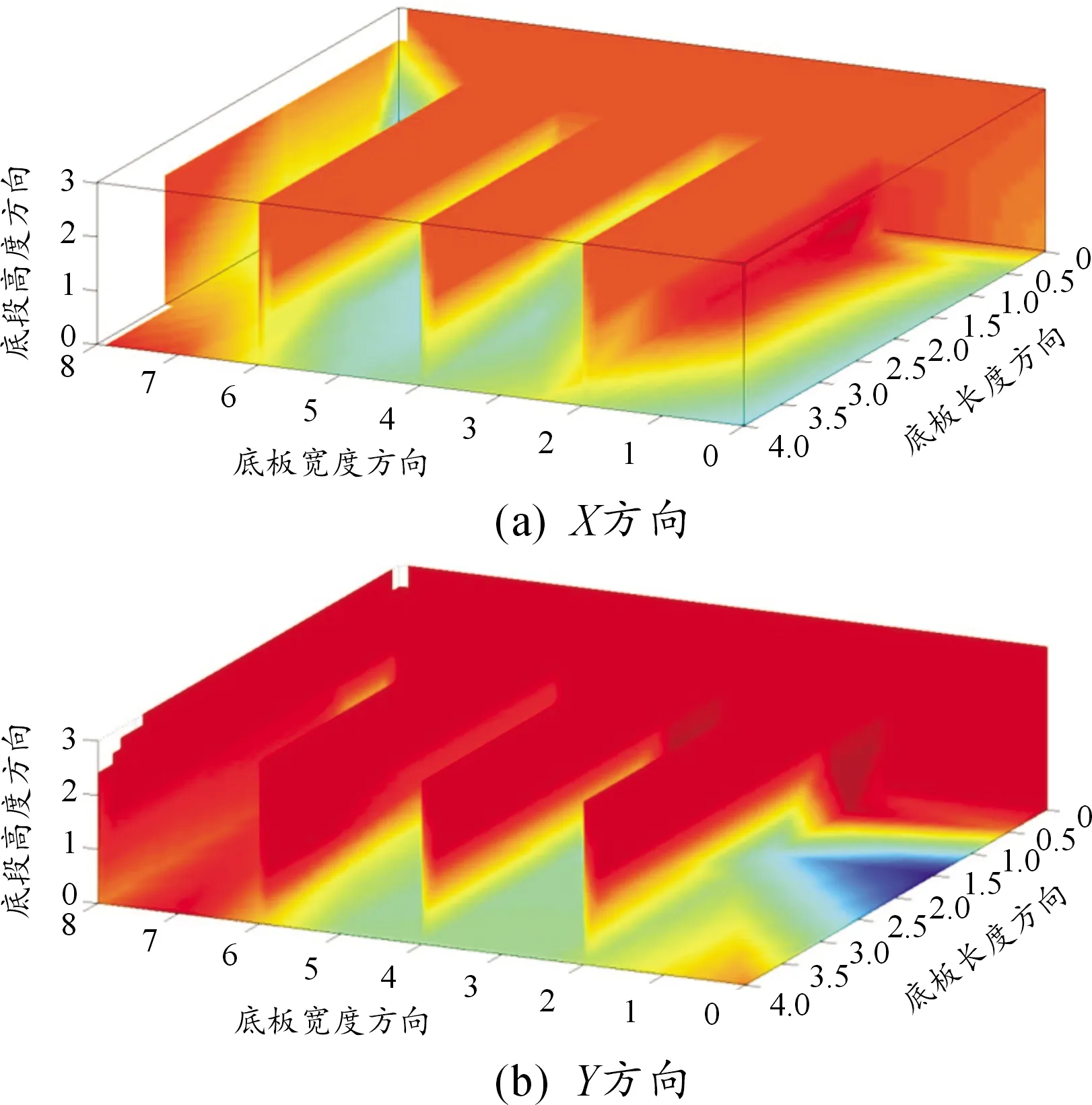
图5 混凝土入仓0.5 d时切片云图
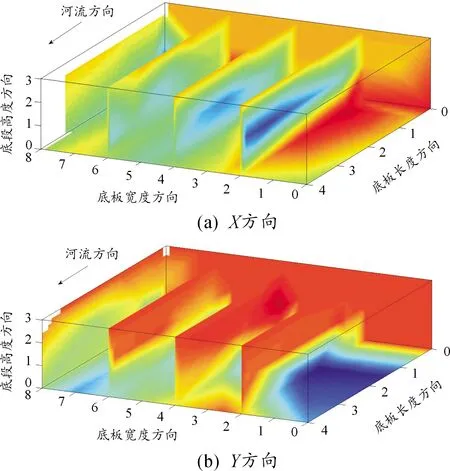
图6 混凝土入仓1 d时切片云图

图7 混凝土入仓4.8 d时切片云图
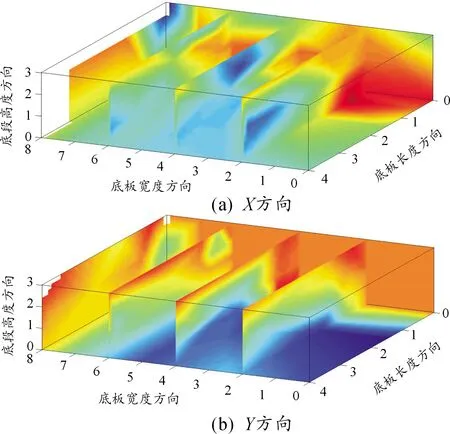
图8 混凝土入仓13 d时切片云图
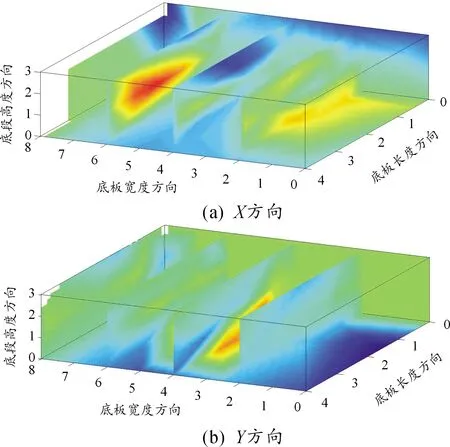
图9 混凝土入仓24.8 d时切片云图
4 桥梁面板混凝土施工期裂缝与温度应力关系规律研究
4.1 温度变化过程
经统计、分析,桥梁面板上、中、下3层温度变化过程趋势据均一致,其中上、下2层通过热传递能量较多,温度较低;中间层温度较高。因此,以上层的第11个测点(编号111)为代表,根据图3可知,入仓后混凝土的温度在0~1 d内迅速上升,然后在1~13.5 d内逐渐下降,再经过13.5~18 d再次升温后,缓慢降至与室外大致相同的温度,温度曲线趋于平缓。
4.2 温度应力、应变与温度关系分析
根据文献[9],混凝土单元某时刻最大温度应力可表示为:
σmax=βEα(T0-T*)λ(1-υ)
(1)
式中:β为能量传递紊动系数,通过待定求解;λ为温度传播系数,通过待定求解;E为混凝土弹性模量,根据实例工程取值为3.41×104;α为混凝土线性膨胀系数,根据实例工程取值为1.05×10-5;T0为混凝土入仓初始温度;T*为待求混凝土单元某时刻实际温度;υ为混凝土泊松比,根据实例工程取值为0.2。
根据实例工程68个测点,共2 475个数据点对式(1)进行线性回归,得到实例工程的温度应力表达式为:
σmax=0.116Eα(T0-T*)1.07(1-υ)
(2)
根据式(2)以及图3可看出,混凝土单元某时刻温度应力、应变与该时刻实际温度呈显著负相关。
4.3 桥梁面板混凝土裂缝与温度应力关系
对实测数据进行统计分析,可以看见桥梁面板混凝土共出现了5条较明显的裂缝,根据裂缝规模从大到小依次命名为B1、B2、B3、B4、B5。实例工程在24.8 d时,各层应变及裂缝情况如图10所示。分析可知:B2、B3、裂缝附近的应变监测显示该区域周围的应变与周围相比有较大变化,这说明早期裂缝的发生可能对应变值有一定关系。裂缝出现时,与其对应的区域应变并没有发现跳变,应变在裂缝出现时依然变化平滑连续;同时,B2、B3、裂缝附近的应变极值相对于其他部位都偏高很多,推断认为,应变极值较大区域附近更可能产生裂缝。
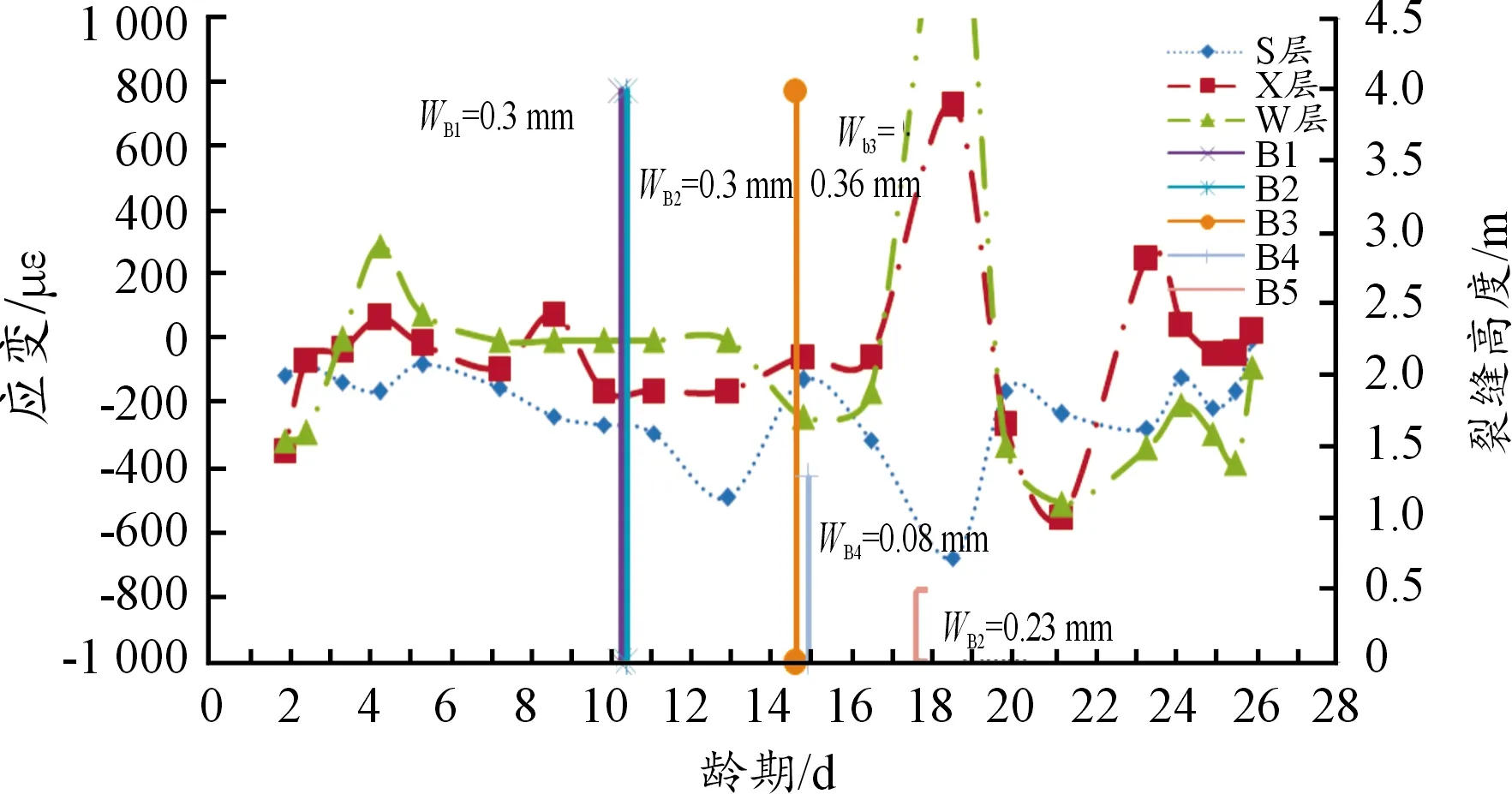
图10 实例工程在24.8 d时各层应变分布及主要裂缝情况
裂缝宽度随时间变化关系如图11所示,前期出现的B1、B2、B3裂缝开始随时间推移而增大,120 d后上述裂缝出现闭合趋势;B4、B5裂缝为后期出现的裂缝,出现时间为105 d左右,裂缝宽度随时间发展而变大。
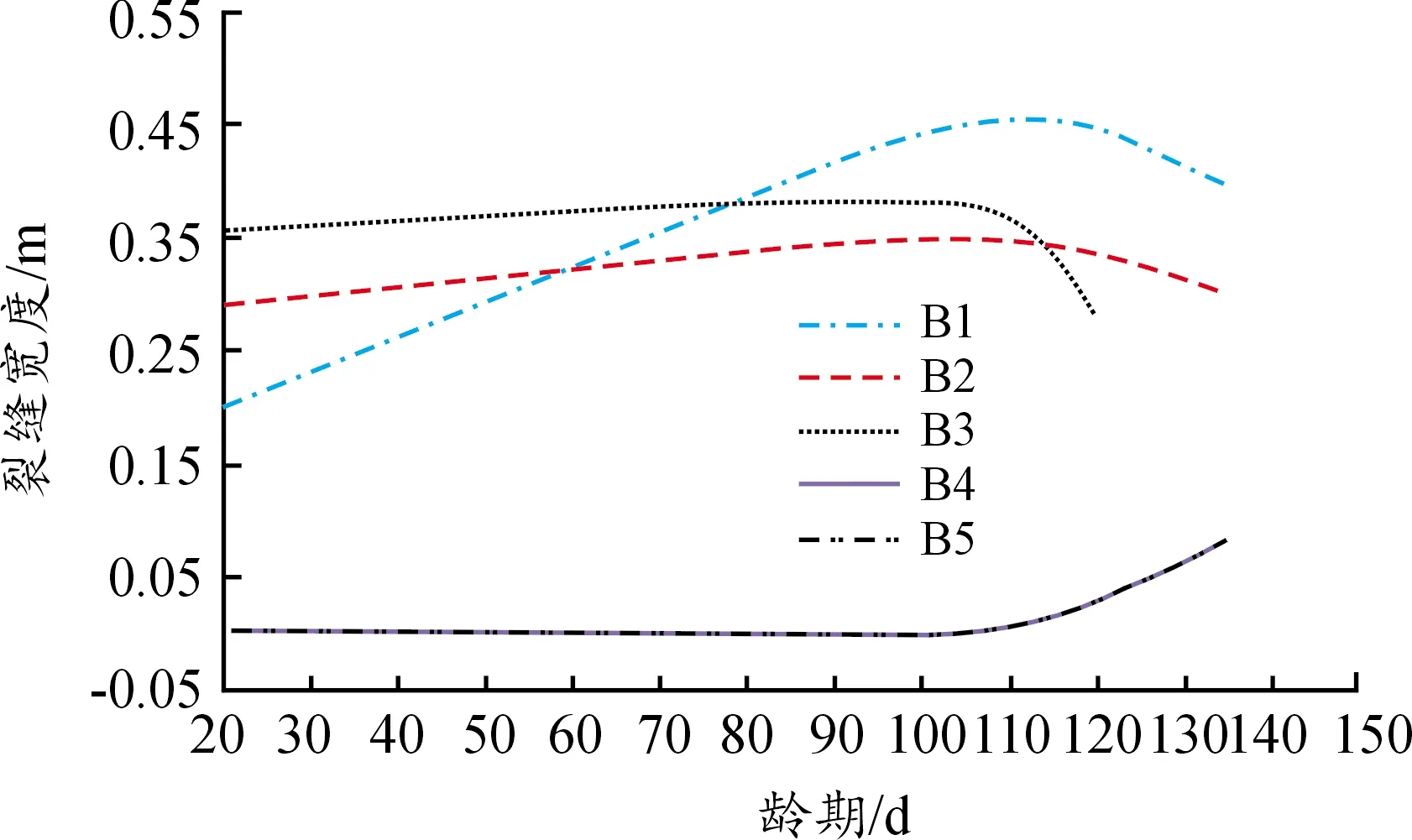
图11 裂缝开展时程曲线
同时,从实例工程温度应力及裂缝发育过程可定性判断,桥梁面板混凝土的入仓温度是早期应变场分布的重要影响因素,裂缝产生的规模与温度应力呈显著的指数正相关。
4.4 临界混凝土入仓温度
根据《大体积混凝土施工规范》,t时刻混凝土抗拉强度可用下式进行计算:
ftk(t)=ftk(1-e-γt)
(3)
式中:ftk为混凝土抗拉强度标准值;γ为混凝土弹性系数,按照文献[10-11]的研究结论,并根据本实例工程的情况取0.35。
同时,当σmax≤1.15ftk(t)时,认为混凝土温度应力未达到承载极限,混凝土不会产生裂缝。因此,结合式(2)(3)可推出混凝土各有限元的临界入仓温度为12.5~19.3 ℃。因此,将实例工程中的混凝土入仓温度控制在12.5 ℃以下,可有效防止混凝土因温度应力产生开裂。
5 结论
1) 桥梁面板混凝土施工期裂缝大小规模与温度应力呈指数正相关,且宽缝区域基本出现在温度应力极值区域;
2)X向应变极值与Y向应变极值相似,但X向与Y向应变的受压中心不一致,X向位于中层位置,Y向则位于底层;
3) 合理控制混凝土入仓温度是有效控制混凝土裂缝的方式,经分析,混凝土各有限元的临界入仓温度为12.5~19.3 ℃。因此将实例工程中的混凝土入仓温度控制在12.5 ℃以下,可有效防止混凝土因温度应力产生开裂。
