差分进化算法寻优下的自动垂直泊车路径规划方法
2022-03-23郑福民
郑福民,段 敏
(辽宁工业大学 汽车与交通工程学院, 辽宁 锦州 121000)
近年来,我国汽车市场不断壮大,国内车辆的数量急剧上升,随之而来的是泊车环境的日益复杂化,对驾驶员泊车技术的要求愈加苛刻[1]。因此,现阶段研究开发自动泊车系统对布局智能驾驶辅助技术具有重要意义。路径规划是自动泊车理论研究的重要一环,目前,国内外学者已进行了大量的研究工作。Kim等[2]基于R-S曲线,将在停车场场景内规划出的48条轨迹公式应用在实际场景中,对泊车路径进行规划。Tazaki等[3]提出以停车场信息为基础,设计多分辨率路线图进行自动泊车轨迹规划。Das等[4]设计了一个自动泊车辅助系统,使车辆通过控制运动先探测外部空间找到泊车位再进行泊车的路径规划。Su等[5]提出了一种基于遗传算法的终点分区二次并行自动停车方法对泊车轨迹进行规划。李红等[6]以B样条路径曲线控制点为变量,以泊车终点处车身方位角最小化为目标,进行了多个泊车工况平行泊车轨迹规划。李想[7]同样基于B样条理论,针对商用车垂直泊车场景进行轨迹规划。张家旭等[8]提出一种基于回旋曲线的垂直泊车轨迹规划方法规划曲率连续的垂直泊车路径。郭夜啼[9]提出了库内双步调整平行泊车路径规划方法,并采用五阶多项式对所设计的圆弧相切路径进行优化改进。
差分进化算法作为一种性能优越的智能优化算法,被成功应用于不同科学技术领域。Wu等[10]提出了一种基于差分进化算法的混合模拟退火算法,解决分布式装配柔性作业车间调度问题。黄良辉等[11]提出了一种基于约束规则协同差分进化算法的建筑BIM施工进度优化方法。董亚明[12]使用差分进化方法进行模型求解,应用于美国PJM电力市场的报价问题。吴文海等[13]提出一种基于改进约束差分进化算法的动态航迹规划方法,以解决三维复杂环境下无人机动态航迹规划问题。田野等[14]提出了一种动态的差分进化算法对直升机空间利用率最大化为目标的人员装载模型进行求解。
本文根据实际泊车工况,对泊车路径进行规划,提出了基于差分进化算法寻优的自动垂直泊车路径规划方法。依据阿克曼转向原理建立车辆运动学模型,综合分析垂直泊车过程中的碰撞情况,建立避障约束函数。规划了一种库外两段圆弧式泊车路径,确定泊车起始区域。然后根据约束条件建立差分进化算法的适应度函数进行二次寻优。结合仿真平台得出,差分进化算法寻优后的路径在路径长度和道路横向占用空间方面均优于遗传算法寻优后的路径。验证了提出的路径规划及寻优方案的安全性和有效性。
1 泊车运动学模型建立及参数说明
泊车时以车辆后轴中心作为参考中心进行建模,车辆运动学模型如图1所示。其中,车辆后轴中心点N坐标记为(xN,yN)。
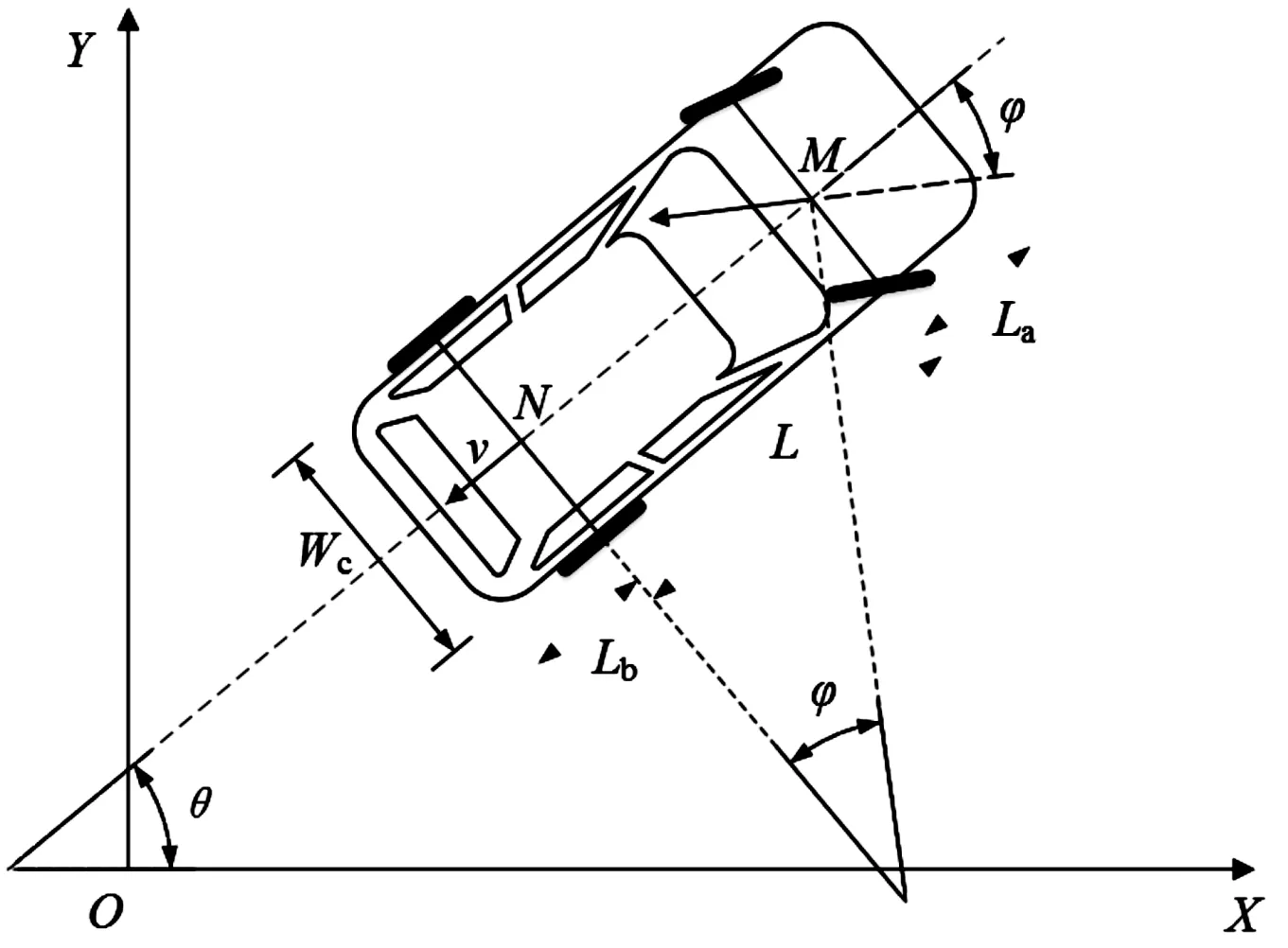
图1 泊车运动学模型
由于车辆自动泊车车速一般低于5 km/h,是一个低速过程,故可以忽略泊车过程中车轮侧向滑动,在研究车辆泊车运动中选取等效车辆后轮轴中心作为参考点。根据图1,得到如下微分方程:
(1)
由式(1)得出等效后轴中心点的运动学方程,可以表示为:
(2)
式中:θ为车辆的航向角;φ为车辆的阿克曼转角,即车辆前轮转向角;L为车辆轴距;v为车辆后轴中心点的速度。
由式(2)可知,车辆后轴中心点坐标以及车身航向角由前一时刻向车辆输入的速度和前轮等效转角决定。
此外,在进行避障分析之前,对所用泊车环境参数及车辆参数进行说明,如表1所示。
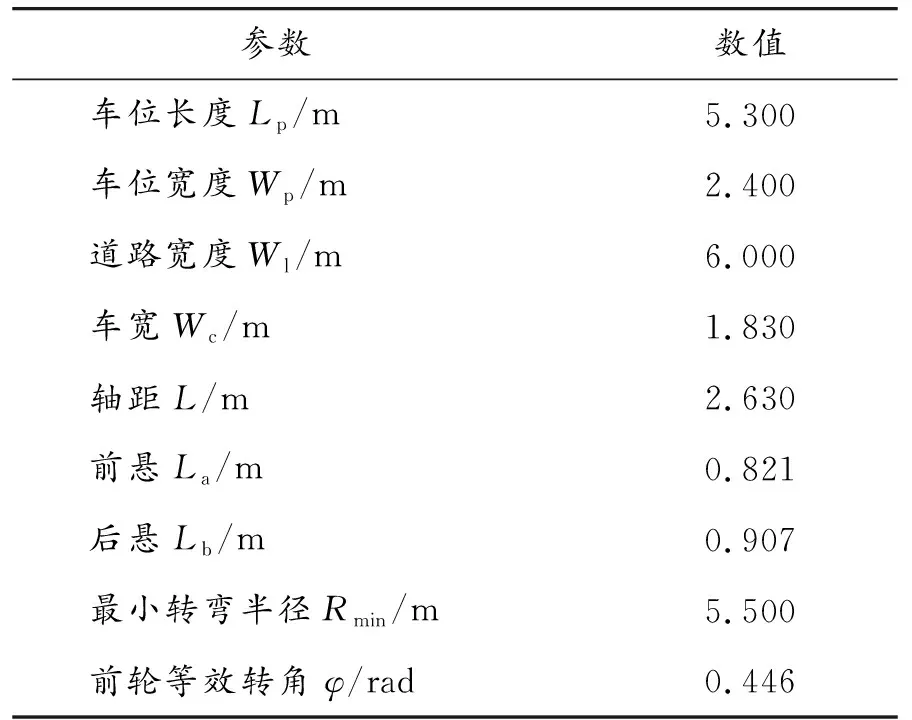
表1 泊车环境参数及车辆参数说明
2 泊车避障分析及路径规划
2.1 车辆处于远离车位侧车道工况泊车避障分析及路径规划
规划合理的无碰撞的泊车路径是泊车成功的前提,也是研究泊车问题的基础。车辆的起始位置不同也就有不同的路径规划方法。为降低泊车过程中车辆的执行难度,本文中规划的路径都是基于车辆最小转弯半径Rmin实现的。车辆处于远离车位侧车道工况时,可采取单步泊车方案,如图2所示。此时,车辆受道路上下边界、泊车位左右边界限制[15]。为了避免碰撞,车辆需要与可能发生的碰撞点预留一定安全距离,从图2可看出,由4个安全参数d1、d2、d3和d4共同决定。本文规定d1=d3=d4=0.1 m,d2=Wl/2+0.1=3.1 m。
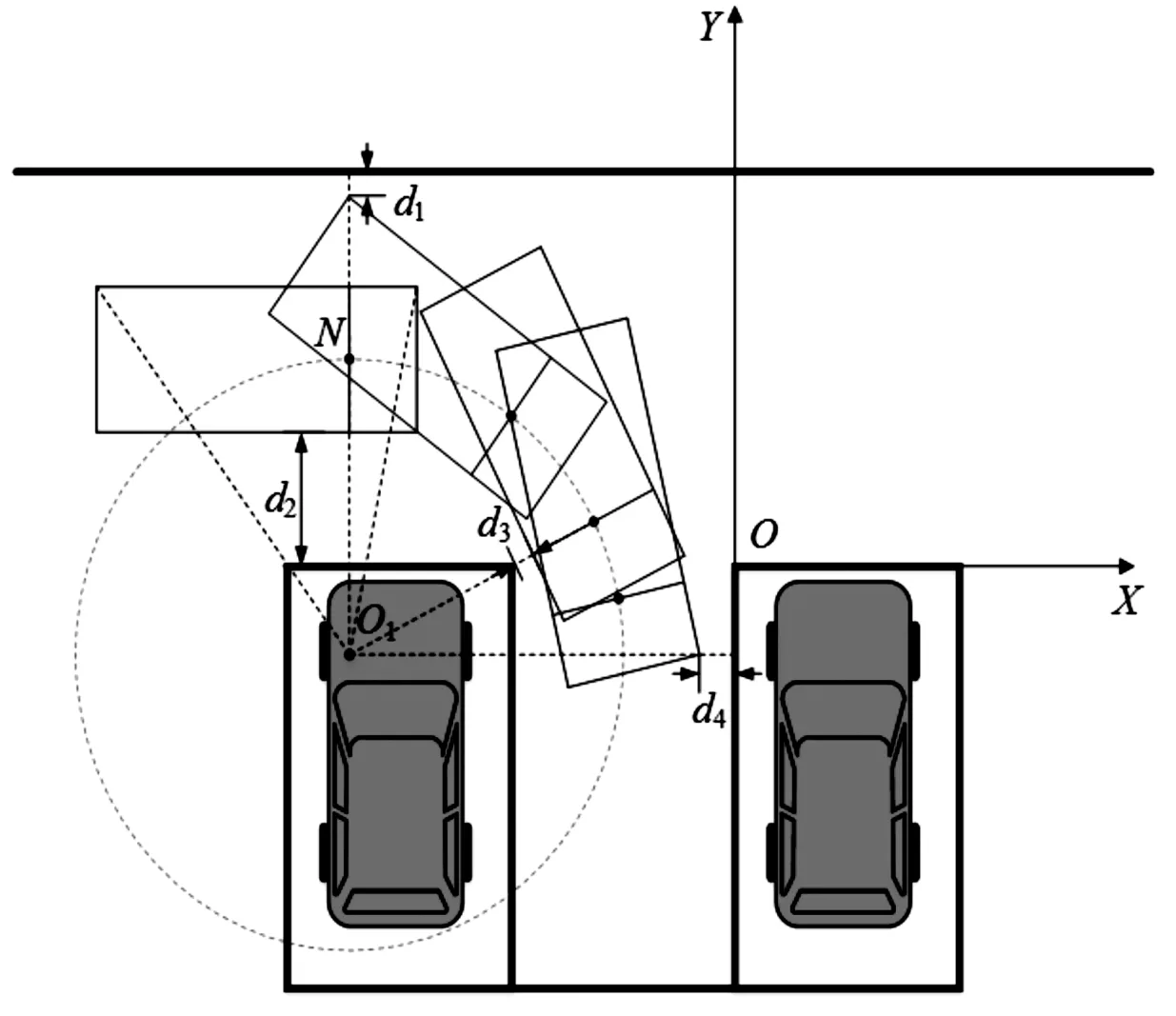
图2 单步泊车避障示意图
以车位右上方点O为圆心建立直角坐标系,点O1为最小转弯半径圆心。根据车辆与道路和目标车位边界的碰撞情况可得到约束关系:
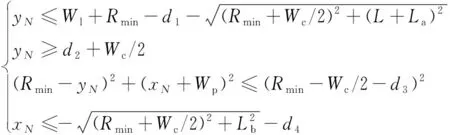
(3)
将泊车环境参数和车辆参数代入上式可得单步泊车起始范围(如图3深色区域所示)。
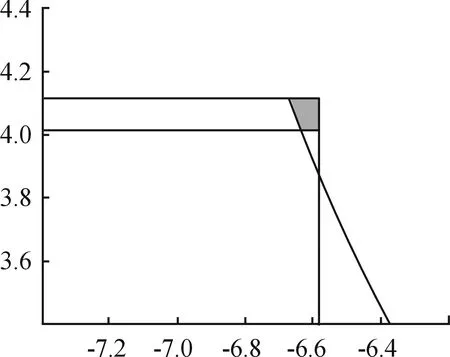
图3 单步泊车起始区域
车辆处于远离车位侧车道工况时调整至图3的起始泊车区域即可开始泊车。
2.2 车辆处于靠近车位侧车道工况泊车避障分析及路径规划
显而易见,上述起始泊车区域和道路边界距离不满足此工况,无法进行单步泊车,此时规划多步泊车策略。
2.2.1路径规划
为减少库内碰撞风险,规划库外两段圆弧式泊车路径。如图4所示,外部传感器检测到目标车辆处于靠近车位侧车道工况时,将启用多步泊车方案。车辆通过外部传感器可获取后轴中心点的起始坐标,调整至目标起始泊车点N1处开始泊车,将方向盘向左打至极限位置,以最小转弯半径Rmin前进至点N2,后轴中心点到达点N2时,挂入倒挡并将方向盘快速向右打至极限位置后退至处于泊车位中心线的点N3,然后回正方向盘,继续垂直后退,当后轴中心点退至点N4时结束泊车。
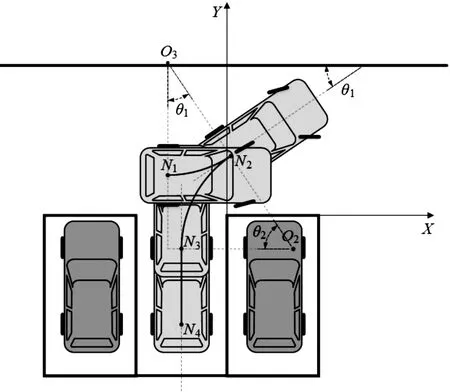
图4 库外两段圆弧式泊车路径
2.2.2避障分析
同样,多步泊车过程中,为了避免车辆与道路和车位发生碰撞,也需预留一定安全距离,如图5所示,由5个安全参数d5、d6、d7、d8和d9共同决定。规定d5=d6=d7=d8=0.1 m,d9=Wl/2+0.1=3.1 m。

图5 多步泊车避障示意图
以车位右上方点O为圆心建立直角坐标系,点O2、点O3为最小转弯半径圆心。泊车起始点N1的坐标记为(xN1,yN1)。泊车拐点N2的坐标记为(xN2,yN2)。泊车回正点N3的坐标记为(xN3,yN3)。第1段圆弧对应的弧度为θ1,第2段圆弧对应的弧度为θ2。
点O3坐标为:
(xO3,yO3)=(xN1,yN1+Rmin)
(4)
点O2坐标为:
(5)
点N2坐标为:
(6)
结合图2和图5易知,点Q为点N的等效点。由式(8)可知点Q坐标为:
(7)
可以得出道路边界对车辆的约束关系式为:
(8)
2.2.3起始位置确定
合理的起始位置决定了多步泊车的安全性和可行性,所以确定起始点是泊车路径规划中的关键环节。
结合上述避障约束关系式,为保证车辆结束泊车时后轴中心点在泊车位中线上,由几何关系进一步可以求得θ1的余弦:
(9)
并且有如下关系:
xN1=Rmin-Wp/2-2Rminsinθ1
(10)
所以求得泊车起始点轨迹为:
(11)
将车辆及车位参数代入式(8)和式(11)中可求得起始范围如图6深色区域所示。

图6 多步泊车起始区域
3 路径二次寻优
规划安全的路径是车辆完成泊车的前提,然而精确、高效的泊车系统是以最优化后的泊车路径为基础的。泊车路径长度和道路宽度占用都是须注意的优化目标。考虑到前文提及的泊车结束时车辆后轴中心停在车位中心线的约束条件过于苛刻,故放宽此条件至车辆后轴中心停在车位中心线的±0.2 m。
差分进化算法是一种基于群体差异的启发式随机搜索算法。与遗传算法相同,作为智能优化算法,主要包括变异、交叉和选择3个基本操作,通过随机生成起始种群,以种群中每个个体的适应度值为选择标准不断地进化,保留优胜的个体,引导搜索过程向最优解逼近。不同之处在于,遗传算法根据适应值来控制单一的父代染色体杂交,在其遗传变异后的子代中进行选择,淘汰方式为劣者概率淘汰,在最大化问题中,往往选择适应值大的个体向量。而差分进化算法每个新个体向量是由父代差分向量生成,直接与其父代个体进行选择,淘汰方式为劣者绝对淘汰。显然,与遗传算法相比,差分进化算法逼近效果更为显著[16]。故本文中采用差分进化算法对路径进行二次寻优,参数选取如表2所示。
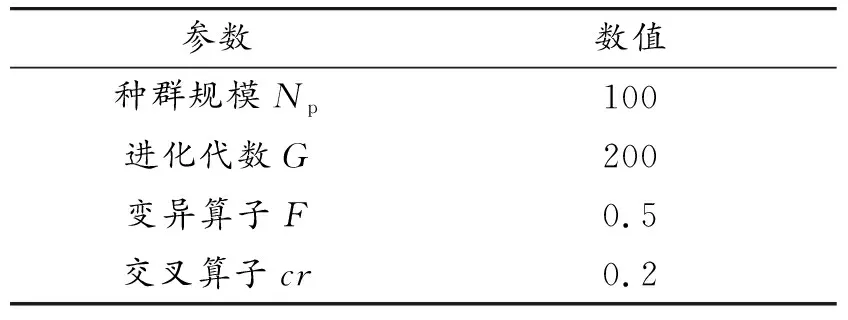
表2 差分进化算法参数
由图7可知,差分进化算法中随机生成初始种群后,通过适应度函数对种群个体进行评价计算,再在循环中进行种群个体的变异、交叉和选择操作,直到满足终止条件时,跳出循环体,输出最优结果。
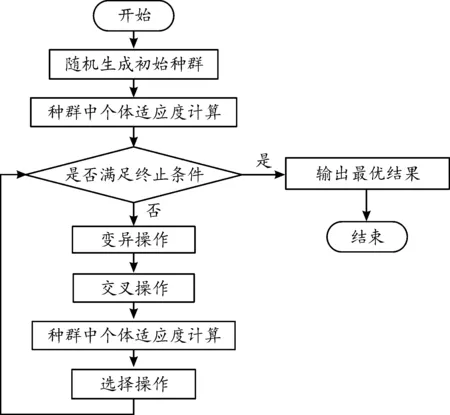
图7 差分进化算法流程图
结合前文约束条件,可得到本文差分进化算法的适应度函数:
FDE(x)=max(min(Wl-yN1-Rmin-(Wc/2-Rmin)cosθ1-
(L+La)sinθ1,xN1+Wp+
(12)
在Matlab中编写相应的M文件,实现输入泊车起始点便可得到寻优前后的泊车路径相关信息。
4 仿真分析
为了突出所提出的差分进化算法路径寻优的优越性,本节通过选取两边界起始点,给出寻优前、遗传算法寻优后和差分进化算法寻优后的路径仿真比较。
在解决遗传算法中的约束优化问题时,通常使用惩罚函数法来将其转化为无约束优化问题。惩罚函数法主要思想为通过对目标函数f(x)增加惩罚项P(x)来构造适应度函数F(x)。其中个体违背了约束条件的程度由惩罚函数来确定,大多采用如下惩罚项函数来表示个体x与第i个约束条件的距离[17]:
(13)
可知个体x与可行域边界的距离总和为:
(14)
式中:ni(x)为第i个不等式约束,ei(x)为第i个等式约束,m为不等式约束条件的个数,s为等式约束条件与不等式约束条件的个数总和。确定了惩罚函数后,结合目标优化函数,建立相应的最优化求解问题自适应函数:
(15)
式中,λi为第i个约束函数的惩罚系数。
将避障约束条件和目标函数相结合,得到本文遗传算法的适应度函数:
FGA(x)=αS(x)+λ1max(0,Wl-yN1-Rmin-
(Wc/2-Rmin)cosθ1-(L+La)sinθ1)+
λ2max(0,xN1+Wp+2Rminsinθ1-
λ3max(0,Rmin-Wc/2-
(16)
在Matlab中编写相应的M文件,其中相关参数选取如表3所示。

表3 遗传算法参数
根据建立的车辆运动学模型,在Matlab/Simulink中搭建仿真平台,仿真结果如图8~图15所示。
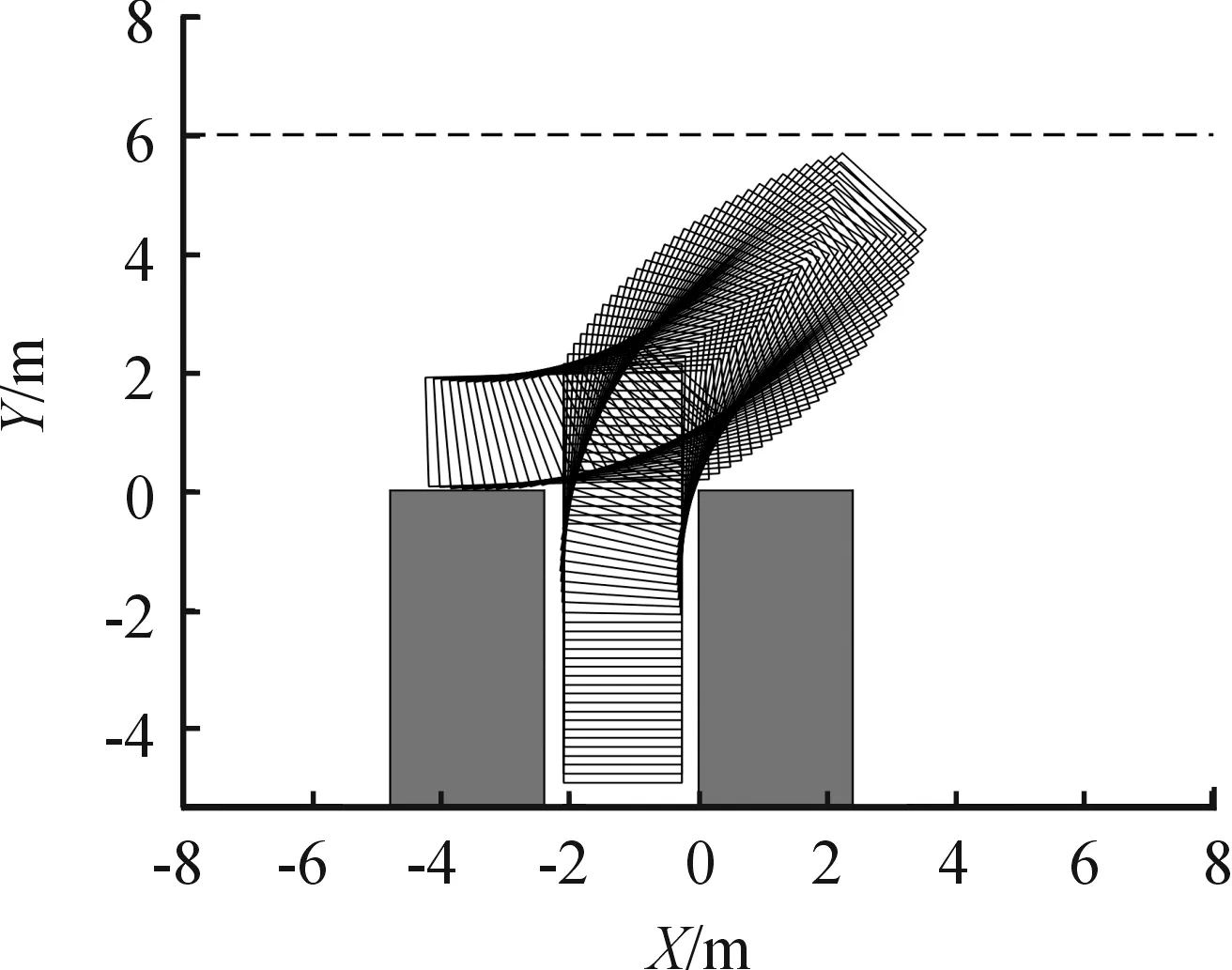
图8 起始点(-3.466,1.015)寻优前仿真图

图9 起始点(-3.466,1.015)遗传算法寻优后仿真图
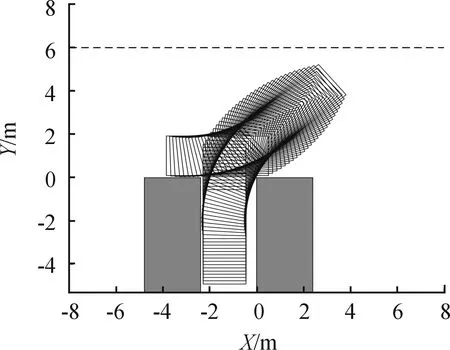
图10 起始点(-3.466,1.015)差分进化算法寻优后仿真图
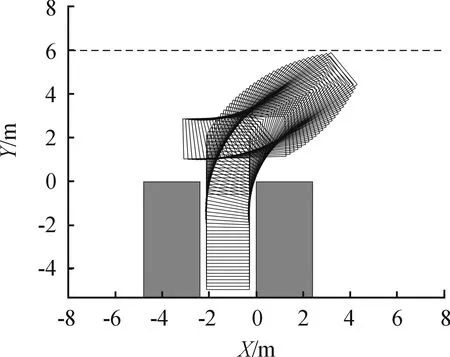
图11 起始点(-2.353,1.985)寻优前仿真图
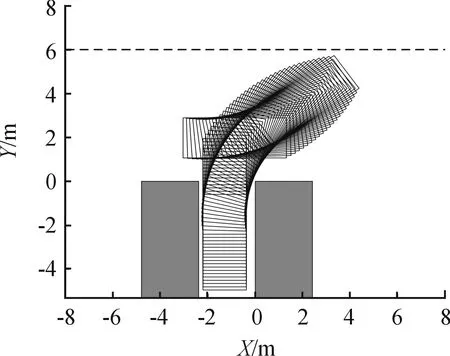
图12 起始点(-2.353,1.985)遗传算法寻优后仿真图

图13 起始点(-2.353,1.985)差分进化算法寻优后仿真图
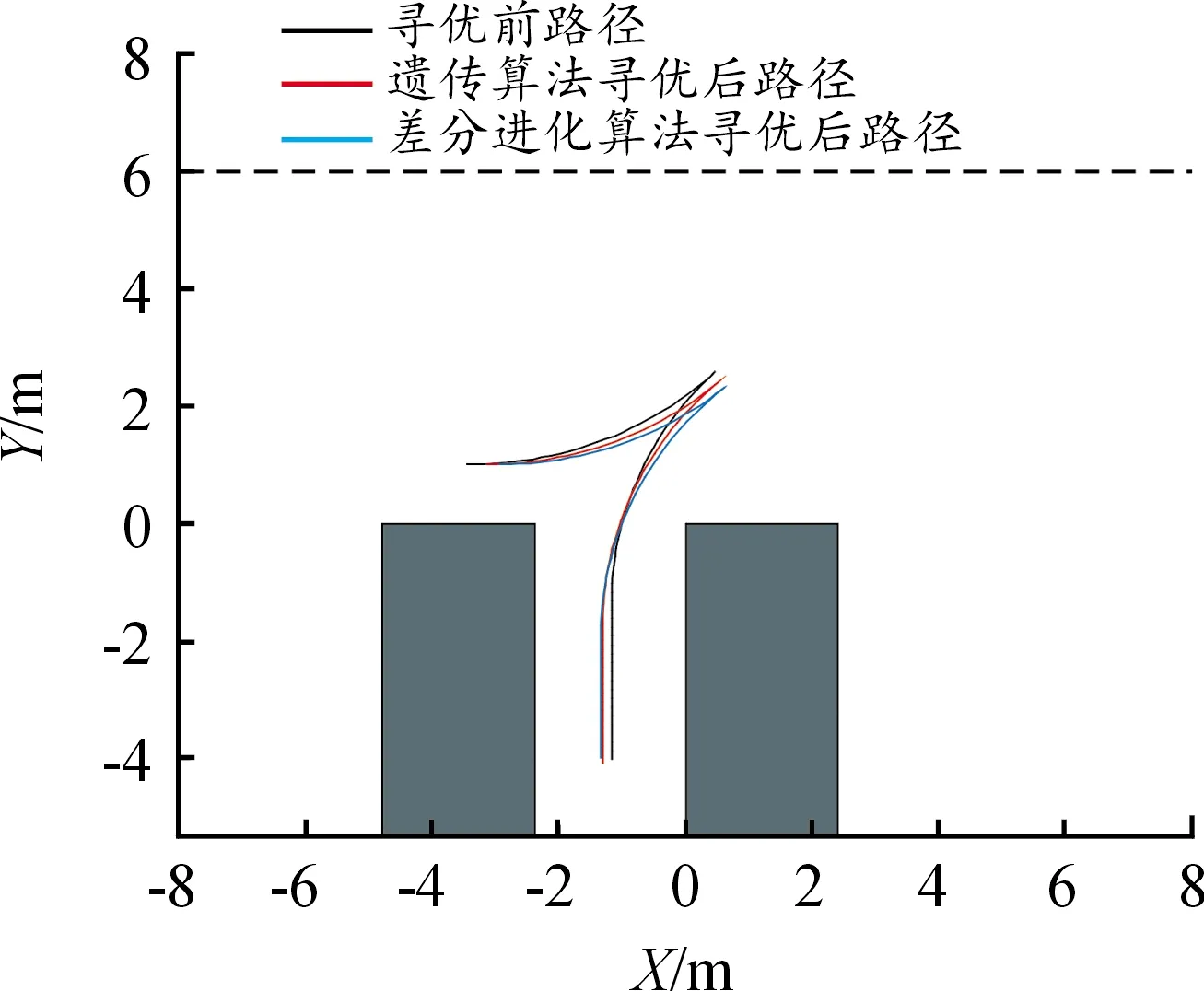
图14 起始点(-3.466,1.015)寻优前后路径对比图
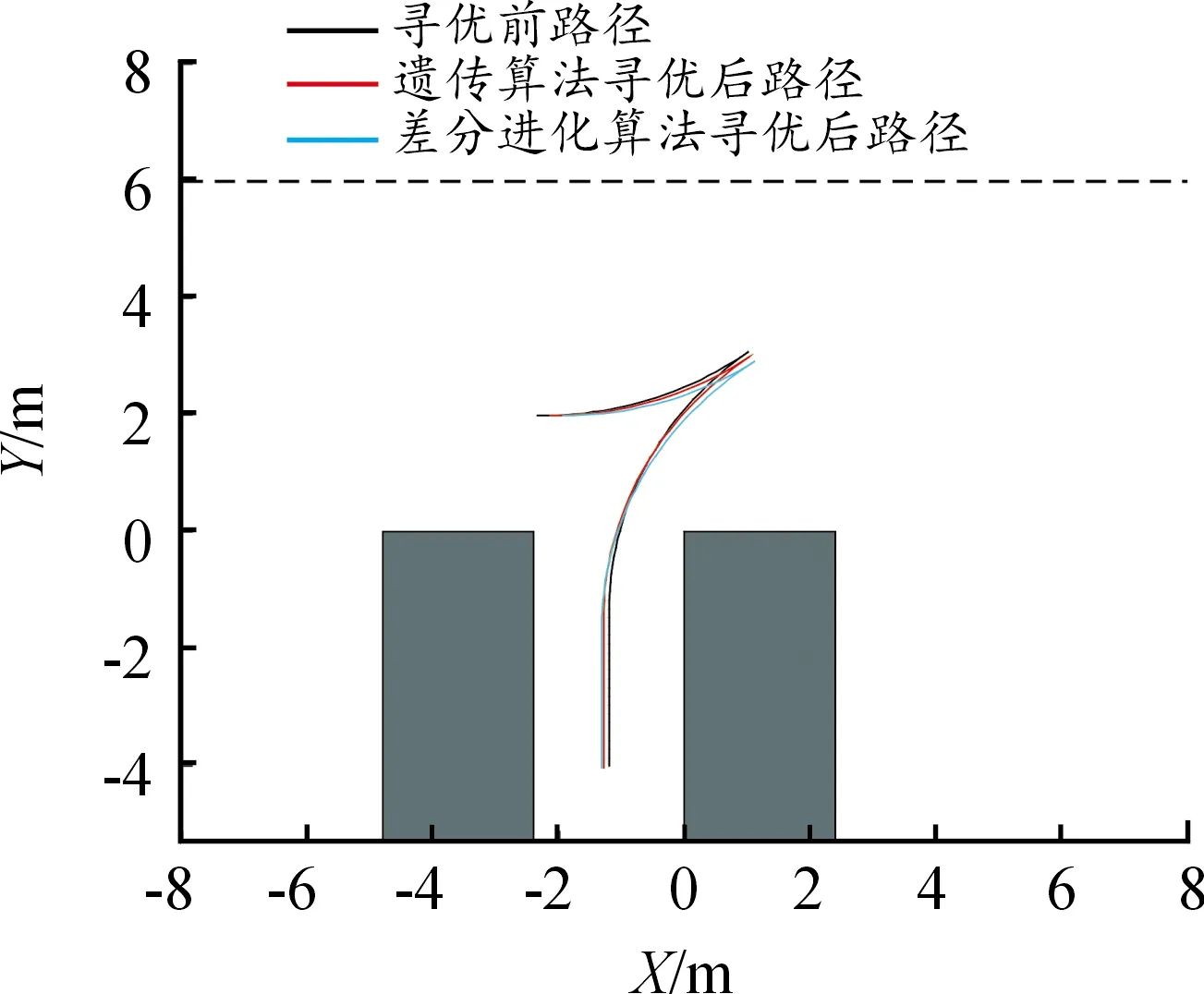
图15 起始点(-2.353,1.985)寻优前后路径对比图
选取两边界点(-3.466,1.015)和(-2.353,1.985)作为目标车辆的泊车起始点,由图8 ~图13的仿真结果可知,寻优前后目标车辆在完成库外两段圆弧式垂直泊车的整个过程中,均未与车位和道路边界发生碰撞。图14为泊车起始点(-3.466,1.015)的寻优前后路径对比图,可以发现,泊车过程中,当目标车辆位于点N2时,差分进化算法路径寻优后,车辆左前端点与道路边界的纵向偏差比寻优前扩大了0.465 m,比遗传算法寻优后扩大了0.175 m,即经过差分进化算法寻优后,车辆所需要的一侧道路宽度得到了进一步减小。泊车结束时,后轴中心点与车位中心线的横向偏差为0.170 m,满足车辆后轴中心停在车位中心线±0.2 m的约束条件。二次路径寻优前的泊车路径总和为11.328 m,遗传算法寻优后的泊车路径总和为10.959 m,差分进化算法寻优后的泊车路径总和为10.736 m,泊车路径总和较寻优前缩短了5.2%,较遗传算法寻优后缩短了2.0%。
图15为泊车起始点(-2.353,1.985)的寻优前后路径对比图,同样可以发现,泊车过程中,当目标车辆位于点N2时,差分进化算法路径寻优后车辆左前端点与道路边界的纵向偏差比寻优前扩大了0.256 m,比遗传算法寻优后扩大了0.169 m,即经过差分进化算法寻优后,车辆所需要的一侧道路宽度得到了进一步减小。泊车结束时,后轴中心点与车位中心线的横向偏差为0.114 m,满足车辆后轴中心停在车位中心线±0.2 m的约束条件。二次路径寻优前泊车路径总和为11.322 m,遗传算法寻优后的泊车路径总和为11.201 m,差分进化算法寻优后的泊车路径总和为11.044 m,泊车路径总和较寻优前缩短了2.5%,较遗传算法寻优后缩短了1.4%。
5 结论
结合车辆运动学约束分别建立了2种泊车工况的边界避障约束。针对车辆处于靠近车位侧车道工况规划了库外两段圆弧式泊车路径,并采用差分进化算法进行二次寻优。利用Matlab/Simulink,通过与寻优前路径和遗传算法寻优后路径进行仿真分析对比。结果表明:此方案的泊车路径在长度和道路宽度占用方面均有改善,能使车辆安全有效地泊入车位。验证了所提出的泊车路径规划方法的高效性和可行性。
