非结构化道路的无人车MFAC大曲率横向控制方法研究

叶 心，马 凯，陈 静，张 腾，卢金涛，盛刘振

(重庆理工大学 车辆工程学院; 汽车零部件先进制造技术教育部重点实验室， 重庆 400054)

近年来，无人驾驶汽车日渐成为汽车研究领域的热门方向，而汽车的各种自动驾驶行为的实现主要依赖于感知、决策、控制，其中横向控制是无人驾驶汽车运动控制的核心问题之一。

当前采用的预瞄式横向控制方法，主要分为两类：一类是考虑不同驾驶员特性的预瞄行为，另一类是基于车辆当前位置与参考路径之间的位置偏差设计控制器以实现对无人车的反馈控制。前者通过机理建模或系统辨识方法建立驾驶员模型，然后与运动学模型或动力学模型结合成闭环控制系统进行反馈控制，或直接以预瞄驾驶员模型根据期望路径计算出描述汽车运动的物理量，李爽等[1]建立了人车路闭环系统，实现对期望路径较高精度的跟踪。这类控制方法直观、物理意义明确，但控制精度和稳定性取决于驾驶过程模型和闭环系统的精度，而对于汽车这种时变、强耦合、非线性的复杂系统，所得到的模型往往存在未建模动力学因素，使汽车在行驶过程中可能出现失稳或安全事故。后者具备更好的鲁棒性，但实现大曲率转向行驶通常需要精确获取道路曲率以评价位置偏差[2]，刁勤晴等[3]提出的双点预瞄策略采用视觉传感器获取横向偏差和道路曲率，并在预瞄距离调节中加入了道路曲率因素，对于大曲率路径具有良好的跟踪精度，但未考虑非结构化道路，由于缺少一致特征，视觉传感器难以对这种环境进行准确理解与识别，因此，对于非结构化道路的环境感知、预期轨迹检测，通常需要结合预先采集的参考轨迹与具备高精度、实时定位能力的车辆定位系统完成，此时，基于视觉的预瞄策略显然不再适用[4]。

然而，目前针对非结构化路面的预瞄式跟踪控制研究较少，田涛涛等[5]基于GPS定位并以偏格式MFAC控制器实现横向控制，能够在直线或小曲率弯道上实现较高精度的跟踪，但由于在预瞄策略中未考虑道路曲率的影响，在大曲率弯道上行驶时会出现转向机构过早响应的情况。为此，本文提出一种适用于非结构化道路的无人车预瞄策略，在预瞄距离调节策略中综合考虑前方道路弯曲度和车辆当前位姿信息，并与PID型无模型自适应控制器结合，然后采用引入局部社会因子的改进粒子群算法实现对控制器的参数整定，使无人驾驶汽车以GPS轨迹点序列作为目标路径，在转向控制过程中实时根据道路弯曲度和车速调节预瞄距离，实现对大曲率路径较高精度的稳定跟踪。最后，基于Matlab/Simulink仿真平台进行模拟跟踪，验证了横向控制算法的有效性。

1 无人车横向控制系统

1.1 控制系统模型

本文构建的无人车无模型自适应(MFAC)大曲率横向控制系统如图1所示。预瞄策略模块通过参考路径信息和汽车位姿信息动态调节预瞄距离和预瞄序列，并计算车辆在实际预瞄点处的预瞄侧偏角α；MFAC控制器采用单输入单输出结构，输入变量为预瞄偏差角α，输出变量为前轮转角δ。

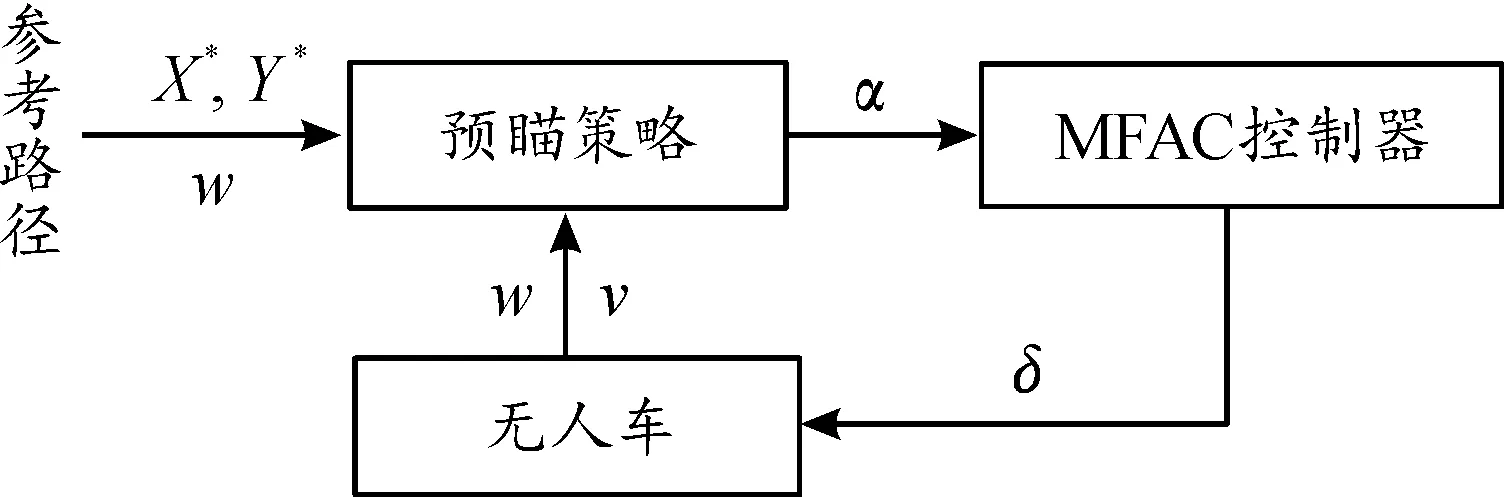
图1 无人车MFAC大曲率横向控制

1.2 线性二自由度汽车动力学模型

为便于分析，将汽车模型简化为线性二自由度汽车模型，其运动微分方程[6]可以表示为:

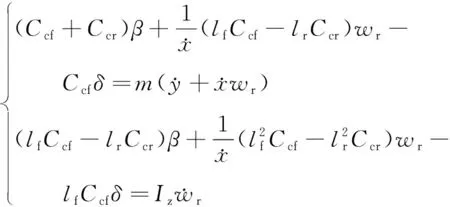
(1)

式中：Ccf、Ccr分别为前后轮总侧偏刚度(kN/(°))；Iz和m分别为车辆的转动惯量及质量(kg·m2和kg)；β为质心侧偏角(°)；lf和lr分别是汽车质心与前轮轴间距和汽车质心与后轮轴间距(m)；wr和δ分别为横摆角和前轮转角(°)。

2 可变序列预瞄策略

2.1 基本概念

驾驶员在行驶时，通常会参考路径上汽车前方某一点，这一点称为预瞄点Q，如图2所示。控制器在实现无人车跟踪控制时以车辆与路径偏差程度为评价指标，定义为预瞄偏差角[7]，预瞄偏差角是指预瞄点与汽车当前点的连线和汽车当前航向之间的夹角α，当预瞄偏差角α趋于0时，汽车将始终朝着预瞄点移动而跟踪上期望路径，此时横向控制问题也就转换为预瞄偏差角跟踪问题。

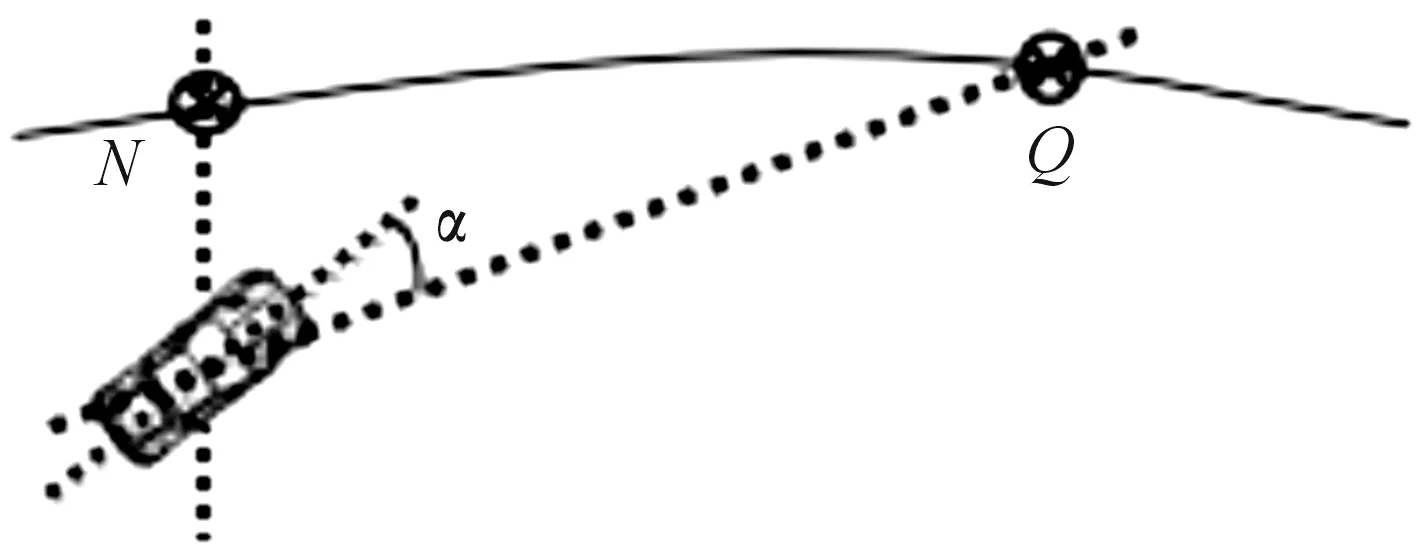
图2 预瞄点

2.2 预瞄方式

如图3，除在参考路径上选取一个预瞄点C1作为实际预瞄点外，其余预瞄点CI均选取在实际预瞄点前方(假设车头方向代表前)，且仅用于获取实际预瞄点前方一段定长参考路径的信息，以评价即将驶入路段的综合弯曲程度。

图3中，XOY是GPS轨迹点序列转化为直角坐标后的全局直角坐标系，C为汽车当前点，C0为参考路径上离汽车当前点最近的GPS轨迹点，C1为汽车实际预瞄点，CI(I=1,2,…,i-1,i)为在参考路径上获取的预瞄点序列，且每个预瞄点坐标可以表示为(XI,YI)，其中wI仅代表每个坐标点(XI,YI)显含的航向角信息。将预瞄距离定义为期望路径上距离汽车当前位置最近的点C0与实际预瞄点C1的弧长距离。车辆定位系统具有实时采集车辆经纬度数据的特点，采集到的GPS轨迹实际上是一系列与时间相关的经纬度坐标，为便于计算，需要将其转换到平面直角坐标系上[8]，如式(2)所示。

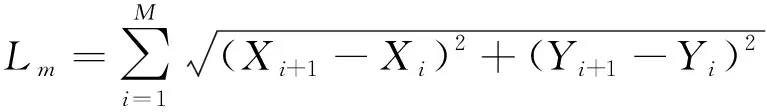
(2)

式中:M代表实际预瞄点C1与C0间包含的轨迹点个数，Xi表示C1与C0间第i个轨迹点的横坐标，Yi表示C1与C0间第i个轨迹点的纵坐标。

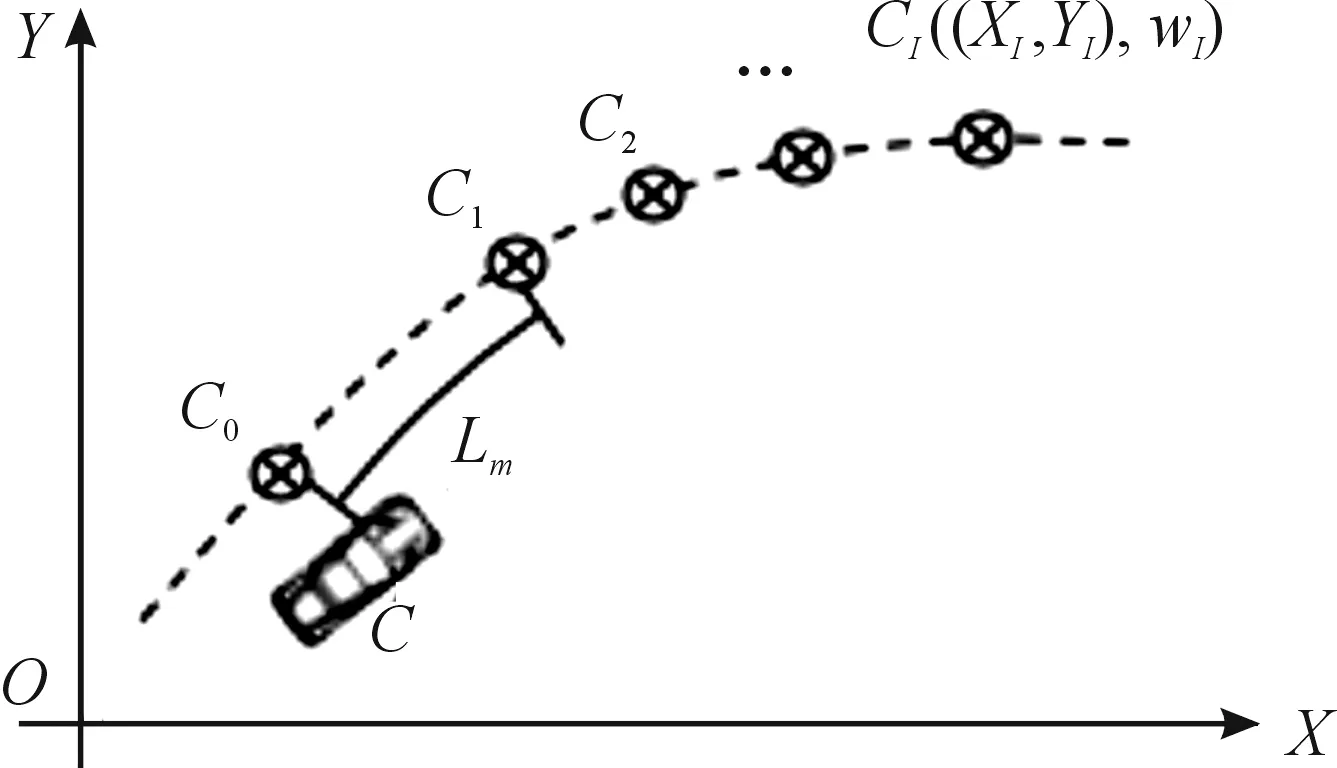
图3 预瞄方式

在评价道路弯曲程度时，对于离散GPS轨迹点而言，求取道路曲率通常需要先对坐标进行拟合，或是采用数值近似的方式计算，实现起来较为复杂。如赵凯等[9]针对道路曲率变化的描述提出了多点预瞄策略，通过前视一段距离获取多个等间隔预瞄点，以每个预瞄点处的切线与车辆前进方向的夹角综合确定路径的弯曲程度。但考虑到预先采集的参考轨迹离线数据中包含有航向角信息，充分利用航向角信息和车辆自身航向角因素判断前方路径的弯曲程度，如图4所示，EON为大地坐标系。道路弯曲程度可以用式(3)表示。

(3)

式中:S代表道路弯曲度，w0表示汽车本身的真北航向角，w1表示汽车前方某段参考路径的第一个离散轨迹点的真北航向角，wi表示w1前方第i个离散轨迹点的真北航向角，D表示计算当前道路弯曲度时所取路径内所包含真北航向角的个数。

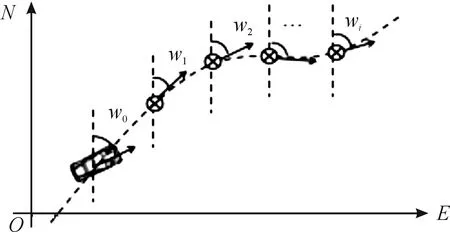
图4 道路弯曲度

2.3 预瞄距离调节策略

预瞄距离的选取直接影响无人车的预瞄跟踪效果。若预瞄距离过大，虽然能提高汽车跟踪的转向轻便性和车辆稳定性，但是会造成车辆到达预瞄点响应时间变长和大曲率转向时转向机构提早响应的情况。若预瞄距离过小，车辆对前方道路的预见性变差且车头易发生摆动[10]。

传统预瞄距离的选取通常是仅与车速相关的单项式，对不同曲率道路的适应性较差。考虑到实际驾驶员在道路上驾驶汽车行驶时，会根据车速和前方道路弯曲程度选择恰当的预瞄距离，以提高驾驶的稳定性和驾驶行为的平滑性，为确保无人车在弯曲度变化较大的路径上以较高精度行驶，在文献[11]的基础上考虑车速v和道路弯曲S对预瞄距离L的影响，预瞄距离调节算法如式(4)所示：

(4)

式中：L0表示预瞄距离初始固定值，k1、k2和σ均为权重因子，k1体现车速与预瞄距离的关联程度，k2、σ均体现道路弯曲度与预瞄距离的关联程度，利用式(4)可以求得实际预瞄点前方一段参考路径的道路弯曲度S。本文中，根据多次测算结果，取L0=1 m，k1=0.3，k2=80，σ=1。

3 PID型无模型自适应控制器设计

无模型自适应控制作为一种数据驱动控制方法，仅利用受控系统的在线I/O数据直接进行控制器的设计和分析，用于大曲率横向控制能够避免对无人车的复杂机理建模，此时控制预瞄偏差角趋于0就能实现无人车大曲率转向行驶时的跟踪控制。因此，本文将无人车横向控制系统转换为预瞄偏差角跟踪控制系统，并设计基于全格式动态线性化的无模型自适应控制器。

考虑无人车横向控制系统为单输入单输(SISO)离散时间非线性系统，即：

α(k+1)=f(α(k),…,α(k-ny),

u(k),…,u(k-nu))

(5)

式中，α(k)∈R、u(k)∈R分别表示无人车系统在k时刻的实际预瞄偏差角和前轮转角，ny和nu是2个未知的正整数。通过在线性化时充分考虑当前时刻某个长度的滑动时间窗内所有控制输入变化量和系统输出变化量对下一时刻输出变化量的影响，将无人车横向控制系统转换为式(6)的全格式动态线性化模型：

(6)

认为无人车横向控制系统在k+1时刻的实际预瞄偏差角变化量α(k+1)-α(k)与滑动时间窗口[k-Lu+1,k]内所有前轮转角输入变化量和在滑动时间窗口[k-Ly+1,k]内的实际预瞄偏差角变化量有关，Lu和Ly称为系统的伪阶数。由于无人车系统在大曲率转向行驶工况下的动力学机理和结构变化十分复杂，Lu和Ly的选取理论上应尽可能地接近真实系统，但考虑到计算负担和控制系统的简捷性，本文取Lu=2，Ly=1。

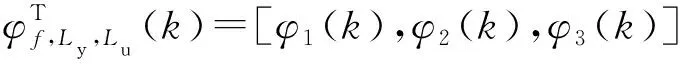
根据全格式动态线性化数据模型给出MFAC控制律，由于该控制律在结构上与PID相似，又称为PID型无模型自适应控制方案：

(7)

式中：α*(k+1)表示k+1时刻的期望预瞄偏差角，ρi∈(0,1],i=1,2,3，λ>0，μ>0，ε为一个小正数。

4 基于改进粒子群的控制器智能调参

无模型自适应控制器能够利用被控系统的在线I/O数据在线调整参数，相较于PID控制器在非线性复杂系统上具有更好的控制性能和自适应性且计算简单，是一种低成本的控制器。但为了设计无模型自适应控制器，必须自选关键参数ρ、η、λ、μ、φf,Ly,Lu(1)，研究表明，上述参数取值不同，控制进程和结果将不同[12]。由于目前尚无一套成熟的人工调参经验方法，有研究者对无模型自适应控制器参数整定问题进行了研究，金尚泰等[13]基于虚拟参考反馈整定方法选定紧格式无模型自适应控制器最优的伪偏导数初值，王丹娜[14]通过建立无模型自适应控制与PID控制之间的结构联系，将PID整定方法应用于无模型自适应控制器参数整定中。但传统PID整定方法对于控制理论知识要求较高，工程实际应用仍存在困难。

智能算法是解决参数整定问题的另一类有效方案，但目前针对无模型自适应控制参数整定的研究仍然较少，其中粒子群算法(PSO)[15-17]作为一种模拟鸟集群觅食行为的智能算法，以其简单易行的优点被广泛应用于PID控制器的参数整定和众多控制系统的控制性能优化，现有文献业已证明粒子群算法应用于无模型自适应控制器的参数整定时同样具有可行性和有效性。此外，本文所使用的全格式动态线性化模型滑动时间窗较长，此时无模型自适应控制器的参数整定问题本质上是高维优化问题，相较于遗传算法，粒子群算法更适用于此类问题的求解，收敛速度更快而且结果也较为精确。综上，本文采用粒子群算法作为参数整定智能算法，但在实际应用过程中发现存在容易陷入局部极值点的问题。为进一步提高收敛精度，在标准PSO算法中引入局部群体经验[18]。

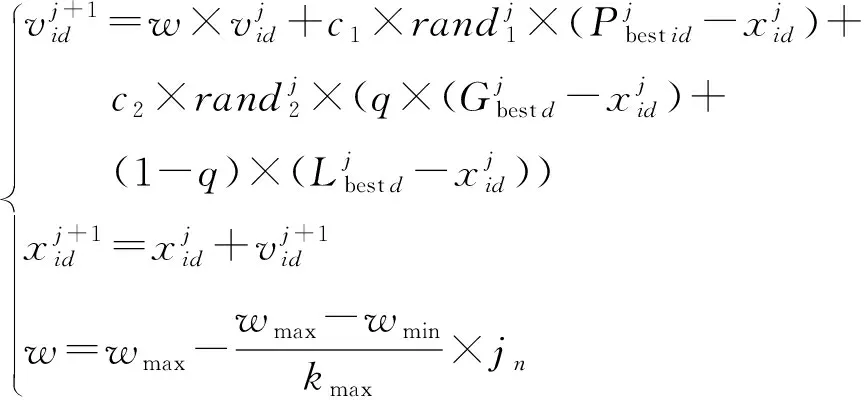
(8)

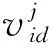
改进后的粒子群算法步骤如下：

步骤1确定参数维度N、粒子群位置和速度范围、学习因子c1、c2、惯性系数w和权重因子q，确定种群规模M，迭代次数n以及局部因子作用半径R并随机初始化各个粒子的位置和速度，然后根据式(9)计算粒子间的距离l以确定每个粒子的初始超球体邻域，xpd、xod表示粒子p与粒子o在d维的坐标，d=1，2，…，N。

(9)

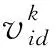
步骤3根据个体极值Pbest、全局极值Gbest和局部极值Lbest的位置，通过式(8)更新每个粒子的速度和位置。

步骤4迭代至最大迭代次数后停止迭代。

本文采用ISTE、IAE指标以及前轮转角增量的加权函数作为适应度函数，其中基于ISTE的性能指标在控制大偏差的同时还可缩短调节时间，IAE指标则对小偏差的抑制能力比较强，而限制前轮转角增量变化能够改善前轮转角变化的平滑性，应用式(10)表征：

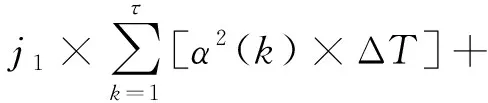
(10)

式中:α(k)表示采样k时刻的离散预瞄偏差角信号；ΔT表示采样周期；τ表示总采样数且τ=t/ΔT；t为仿真时间；j1、j2、j3为权重因子。

改进粒子群算法流程如图5所示。

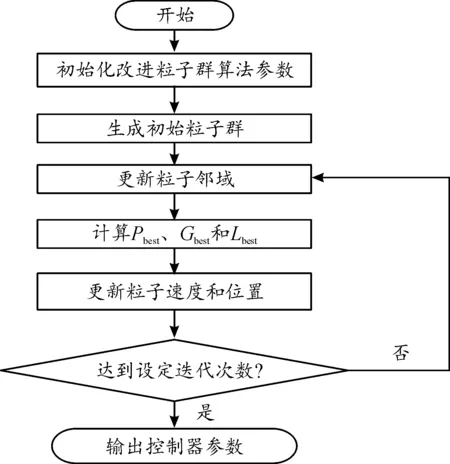
图5 改进粒子群算法流程

5 仿真实验与验证

5.1 无人车MFAC跟踪控制模型的构建

为验证可变序列预瞄式PID型无模型自适应横向控制与基于改进粒子群算法的控制器智能调参方法的有效性，根据前述的汽车动力学模型和控制器设计方法搭建了基于Matlab/Simulink平台的控制模型(见图6)，其中车辆模型主要参数见表1。

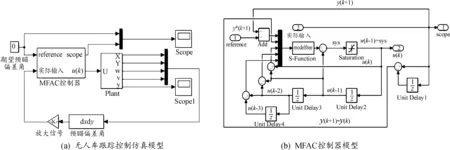
图6 无人车MFAC跟踪控制仿真模型

表1 车辆模型参数

5.2 仿真结果对比分析

5.2.1控制器调参结果对比

为分析不同调参方法下控制器对偏差的响应效果，对比人工选定方法、标准粒子群算法和改进粒子群算法智能调参方法，通过适应度函数(式(10))评价控制效果，式(10)中取j1，2,3=[1,1,100]。

参照GB/T 6323—2014标准设定双移线目标路径并设定车速为20 km/h，仿真步长为0.02 s，可得到不同调参方法下的控制器预瞄偏差角变化曲线和适应度大小，分别如图7和表2所示。

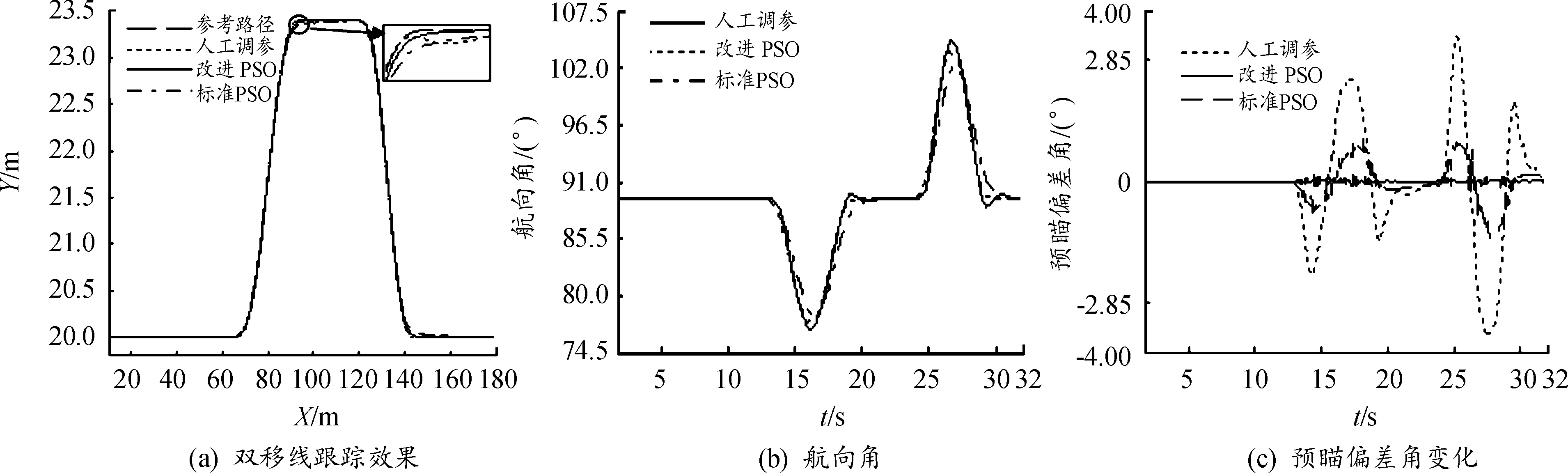
图7 调参效果对比

表2 控制效果

由图7可见，人工调参的控制器虽能消除预瞄侧偏角误差，但在经过连续转向路段时均出现了振荡和超调，此时航向角出现小幅突变，且最终回到直线路段时的收敛速度较慢；经过标准粒子群算法选定参数的控制器在进入连续转向路段后的振荡和超调明显降低，并在回到直线路段时迅速收敛，航向角变化平滑，但仍存在响应速度较慢的问题，其原因在于标准粒子群找到的仅是局部最优点，因此，虽然控制器性能优于人工调参方法，但仍不是全局最优解；而基于改进粒子群算法智能调参的控制器性能的提升则明显优于标准粒子群算法，预瞄侧偏角误差全程控制在极小范围内且响应速度极快。此外，由表2可见适应度函数值对比结果，基于改进粒子群算法智能调参的控制器性能优于标准粒子群算法与人工调参两种方法下的无模型自适应横向控制器，且能够满足连续转向路径下的跟踪精度要求，验证了改进粒子群算法智能调参方法的优越性。

5.2.2可变序列预瞄策略的跟踪效果分析

为进一步分析双移线路径仿真下预瞄距离的变化过程和控制器对偏差的响应，以表2中改进粒子群算法选定初值作为控制器参数，并设定车速为30 km/h，仿真结果如图8所示，其中图8(a)选取实际预瞄点前方1 m长度的道路用以评价道路弯曲度，图8(c)(d)反映无人车的跟线偏差。

由图8(a)可见，此双移线路径的四处转向路段分别对应于图中4处波峰位置，且由于转向处道路曲率不同，波峰的道路弯曲度最大值也有所不同。此时选取的路段长度仅为1 m，对道路弯曲度的判断敏感，因此在经过双移线的2段近似直线路段的第10 s和第16.5 s处道路弯曲度出现2处尖点。图8(b)反映无人车实际预瞄点的预瞄距离随道路弯曲度和车速的变化关系，由于车速不变，此时预瞄距离的变化仅与道路弯曲度有关，并与道路弯曲度呈反比例关系，回到直线路段时预瞄距离出现短暂振荡。由图8(c)可知，由于此时无人车与双移线路径存在航向偏差，为尽快跟踪上参考路径，道路弯曲度考虑了无人车自身航向因素而不为0，但全程预瞄距离变化仍较为平滑。

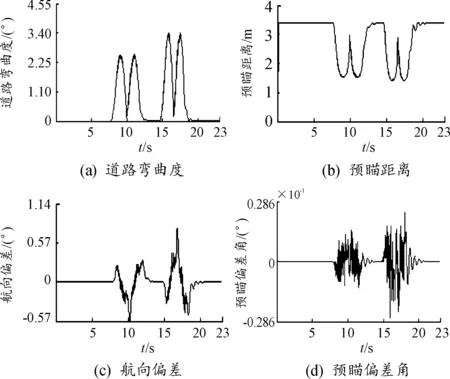
图8 跟踪效果分析

根据图8(c)(d)所示和计算结果，在控制器参数保持不变的情况下，车速改变后PID型无模型自适应控制器仍然具有很好的偏差响应效果，全程航向偏差最大值为0.802 1°，位置偏差最大值为0.06 m，预瞄偏差角最大值为0.229 2°(预瞄偏差角范围为[-180°,180°])。

6 结论

本文提出了适用于非结构化道路的可变序列预瞄式PID型无模型自适应横向控制方法，给出了综合考虑车速和道路弯曲程度的预瞄点及预瞄距离的计算方法，以及PID型无模型自适应控制器的设计方法，并采用改进粒子群算法实现了对控制器的智能调参。结果表明：① 所设计的控制系统能够根据前方道路弯曲度和车速对预瞄距离作出平滑调节且符合驾驶员习惯；② 控制器通过获取预瞄偏差角对前轮转角进行有效调节，确保车辆能以较高精度跟踪目标路径，并且当车速发生改变时，PID型无模型自适应横向控制器仍然具有很好的控制效果，充分发挥了控制器的鲁棒性；③ 所设计的改进粒子群算法智能调参方法能够大幅节省调参成本且相比于人工调参能得到更好的控制器性能。

但是在控制过程中，航向角发生小幅高频抖动可能会影响舒适感，这是由于本文Ly和Lu的取值较小，通过适当增加Ly和Lu的取值使动态线性化模型接近于真实系统，可以使控制器提供更多的伪梯度分量，更好地分担捕获原系统中可能存在的复杂动态。另外，大曲率转向控制通常通过横纵向协同或耦合控制，以达到更好的控制稳定性和舒适性，也更加符合真实驾驶习惯，考虑无模型自适应控制能够推广到MIMO离散时间非线性系统，且能够避开复杂的横纵向耦合建模，下一步将对无模型自适应横纵向耦合控制进行研究。