矿用对旋风机失速信号特征的诊断与分析

陈庆光，邢振想，姜忠瑞，张永超

(山东科技大学 机械电子工程学院，山东 青岛 266590)

在煤矿企业中广泛使用的对旋主通风机，其设计朝着高负荷、高效率、宽稳定工作范围的方向发展，必须面对小流量工况下可能发生的失速、喘振等问题。旋转失速和喘振不仅影响风机稳定的工作范围，而且降低风机运行的可靠性，因此从风机设计到运行过程都应给予足够重视。自20世纪以来，国内外学者围绕压气机、风机等旋转机械失速起始扰动发生的位置、类型和机理等问题，采用数值模拟和实验测量的方法进行了大量研究并取得丰硕成果[1-4]。风机在运行过程中必须避免进入失速状态，否则将可能对风机产生不同程度的损害。因此，若在风机失速发生前就能做出准确的预测，则可根据预警提前采取措施以避免失速的发生。这对于保障风机安全、稳定运行具有非常重要的意义。

要实现风机失速的准确预测，需要能够对失速特征进行快速、有效的诊断。随着信号处理技术的快速发展，国内外学者针对旋转失速发展了不同的诊断方法，一般分为时域分析、频域分析、时频分析。从时域角度，李长征等[5，6]基于统计特征、时间序列分析对压气机喘振进行检测；刘洋等[7]运用自相关分析、互相关分析对压气机失速信号进行处理和分析；Yue等[8]将自相关分析和互相关分析相结合的概率统计方法用作失速预警方法。但时域分析易受噪声干扰、计算耗时过长以及精度不高等缺点。从频域角度，Manas等[1]运用傅里叶分析技术分析了在对旋风机转子1前缘上游位置获得的非稳态套管静压信号；Tegegn等[9]通过快速傅立叶变换分析了周向畸变条件下低速对旋轴流风机内部流场中的非定常压力信号。但频域分析以全局变换为基础，无法识别失速信号的局部特征。时频分析技术是近年来信号处理等领域一个新的研究热点，其中小波分析因具有良好的时频局部性及多分辨分析特性，而被广泛使用并取得大量研究成果[10-13]。然而，现有的关于失速的检测与诊断方法，在工程应用方面还没有达到理想的程度，失速特征的检测与诊断仍是需要深入研究的课题。

针对以上原因，为给矿用对旋风机提供一种有效的失速诊断方法，从频域、时频两个角度揭示风机失速信号的瞬态局部特征，提出一种FFT技术与小波-时频分析相结合的失速诊断方法。本文基于数值模拟获得对旋风机近失速工况下内部流场的非定常压力信号，采用本文所提出的失速诊断方法对失速信号进行诊断分析，以确定失速发生的时刻及失速的特征频率。

1 对旋风机内部流场的数值模拟

研究针对一台矿用对旋式主通风机，其轮毂比为0.62，设计转速为980r/min，前后级叶片数分别为19和17，叶顶间隙为2mm。

1.1 几何模型与网格划分

数值模拟针对对旋风机全流道几何模型进行，由集流器、前级转子、后级转子和扩散器组成，计算网格如图1所示，考虑到模拟计算的效率与精度，用六面体单元对全流道模型进行结构化网格划分，动叶区域采用H-O-H型拓扑。对两级叶轮的叶顶间隙、前缘及尾缘区域进行局部网格加密，在叶顶间隙内布置了16层网格，两级叶轮域局部网格如图2所示。经网格无关性验证，全流道总网格数取551万，其中前、后级叶轮两个子区域的网格数分别为268万和255万。

图1 对旋风机全流道网格

图2 两级叶轮区域网格划分

1.2 数值计算方法与边界条件设置

由于分离涡模拟(Detached Eddy Simulation，DES)技术能够较好地预测旋涡及分离流动，因此本文选择DES模型来模拟湍流。壁面采用无滑移条件；进口给定总压1.01325×105Pa和进气角(轴向进气)。首先进行定常模拟，通过逐步提高出口背压获得收敛解，再以定常解作为初场并加载出口节流阀函数进行非定常模拟，模拟过程中通过减小节流阀开度(减小流量)使风机逐步逼近失速工况，从而获得失速流动信号。所采用的出口节流阀模型函数为：

式中，p1为出口背压，Pa；p0为大气压，Pa；k0为常数；k1为节流阀开度；ρ为密度，kg/m3；V为出口轴向速度，m/s。

1.3 监测点布置

通常风机失速首先发生在叶顶区域，因此，为监测对旋风机失速过程的静压信号，如图3所示，在前、后级叶顶间隙内分别沿周向布置了4个静压监测点，前级相邻两个监测点周向间隔37.89°，后级相邻两个监测点周向间隔42.35°。

图3 前、后级内监测点的布置

1.4 模拟结果与分析

目前判定风机进入旋转失速的方法主要有两种：一是监测风机出口压力与流量是否有明显的下降，二是观察沿叶轮周向均匀布置的监测点所监视的静压或轴向速度的变化情况[14]。

经过多次适度地关小阀门开度，最终发现在同样足够长的时间内，当阀门开度k1维持在0.8时，风机的出口压力与流量尚能维持稳定的周期性变化，如图4所示。从图中还可看出，当阀门开度k1进一步减小至0.7时，风机出口压力的波动趋势明显增强，并在经过10个旋转周期后，出口压力发生突降，并伴随着出口流量的下降，最终二者均稳定在一个较低的值。基于风机所处的运行工况以及性能表现可以推测风机此时已经进入了数值失速状态。

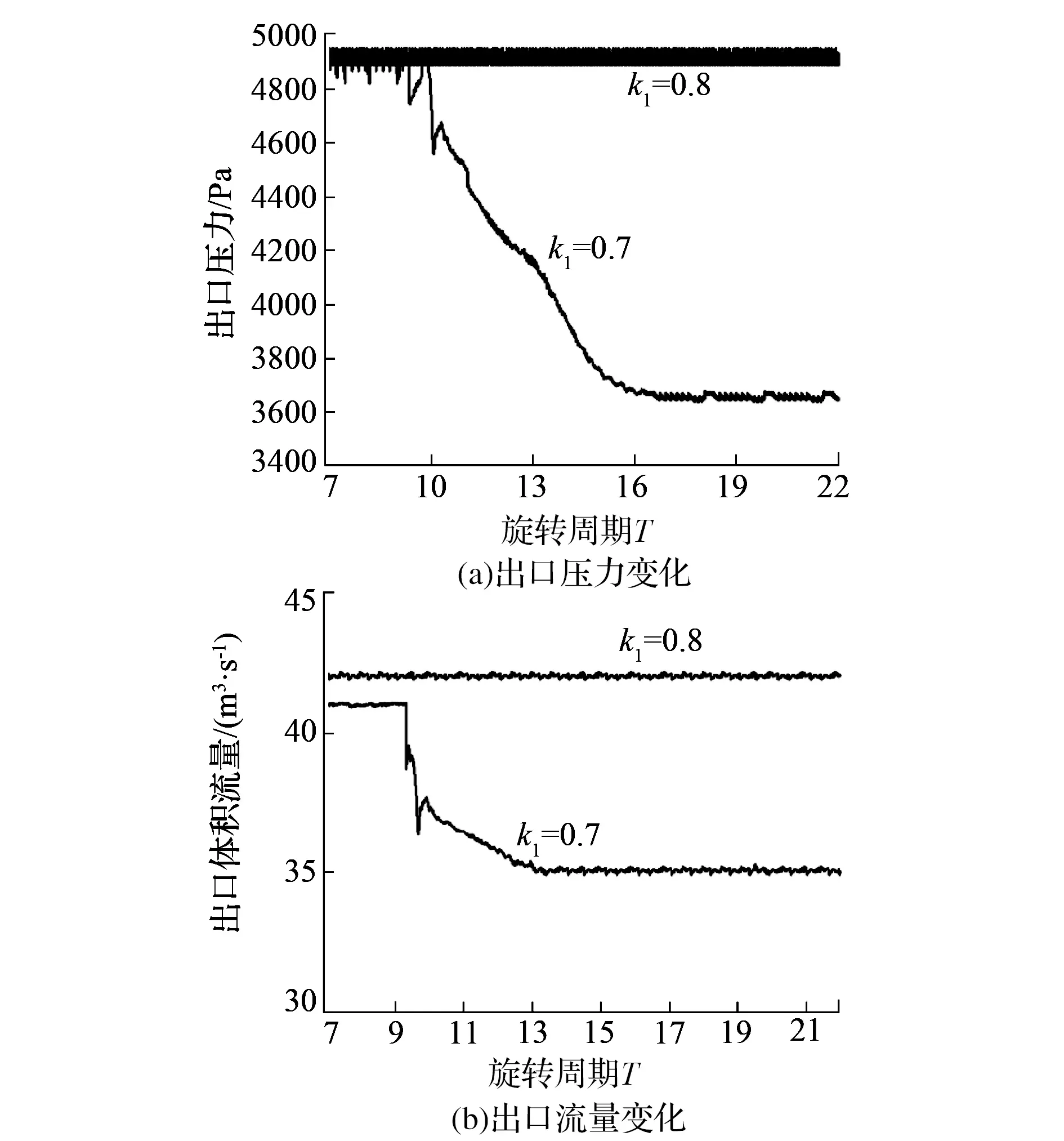
图4 不同阀门开度下出口压力与流量的变化

风机的动态失速过程可以分为三个阶段：近失速、失速发展及完全失速。不同失速阶段两级叶轮部分流道叶顶区域(98%叶高处)的流线分布如图5所示。从图5(a)可以看出，在设计工况下两级叶轮的叶顶间隙流均随主流一起向下流流动，流道内具有良好的流通性，没有形成前缘溢流、尾缘反流。随着风机进入近失速阶段如图5(b)所示，两级叶轮的叶顶间隙流与主流相互作用形成前缘溢流，同时还能看出前级叶轮处来自相邻叶片的叶顶泄漏流绕过尾缘形成了尾缘反流，但后级叶轮没有出现尾缘反流。在近失速阶段，对旋风机前级叶轮叶顶区域同时出现了前缘溢流与尾缘反流，二者作为典型的失速起始扰动特征与Vo[15-20]等提出的“突尖型”失速起始扰动的出现准则一致，证明了对旋风机进入失速状态，失速类型属于“突尖型”失速。

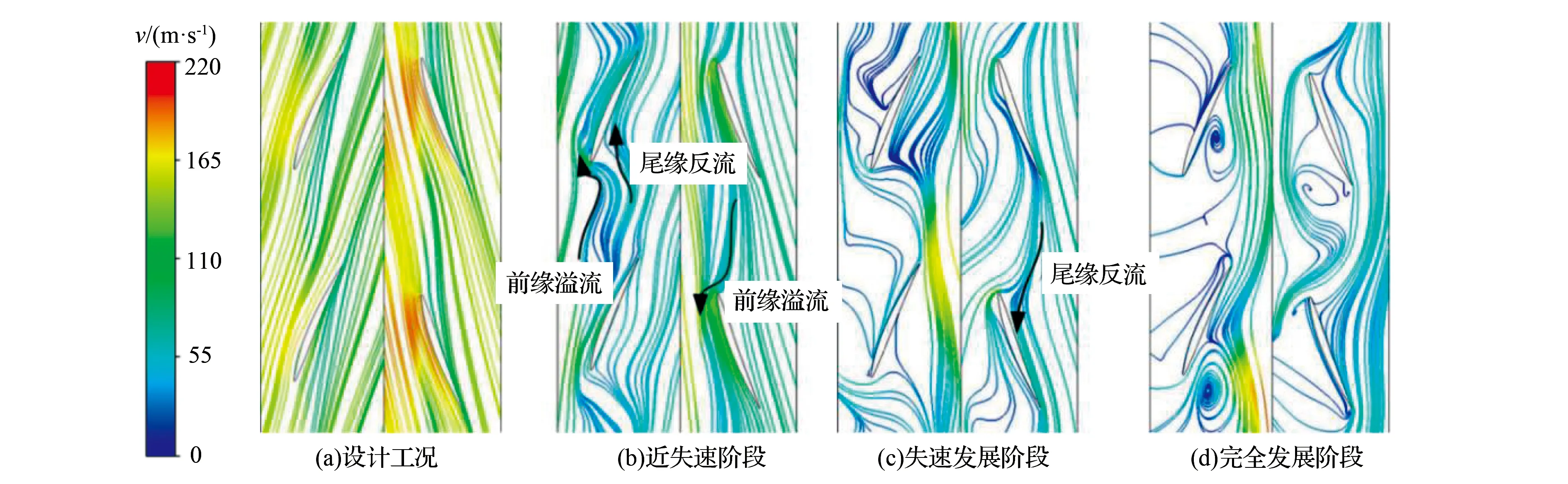
图5 不同失速阶段98%叶高处的流线分布

当风机进入失速发展阶段时，从图5(c)可以观察到后级叶轮中部分叶顶泄漏流穿过叶片尾缘后又向上游流动，直至到达相邻叶片的压力面而形成了尾缘反流。从图5(c)还可以看出，两级叶轮在近失速阶段所形成的前缘溢流所涉及的范围及强度均变得更大，与叶片吸力面附近的分离流一起演变成为大范围的通道反流，并且前级叶轮中的通道反流范围及强度都大于后级叶轮。最后风机进入完全失速阶段，从图5(d)可以看出两级叶轮通道内的反流区域较失速发展阶段进一步增大，前级叶轮的压力面附近还形成了较大的失速涡，该失速涡是通道反流与部分堵塞流体在叶片的推动下相互作用而形成的，该失速涡与其余的通道反流一起占据了大部分流道。同时两级叶轮尾缘附近的流线均聚集在一起而没有向下游展开，这说明在完全失速阶段有大量流体聚集在两级叶轮内。

2 失速信号的诊断与分析

基于数值模拟结果，从频域、时频两个角度对风机流场内监测点的静压信号进行分析。首先通过对原始压力信号进行快速傅里叶变换(Fast Fourier Transform，FFT)，确定失速发生时频率的主要成分及其变化；然后进行小波-时频分析，确定失速发生的时间，技术路线如图6所示，其中ca和cd分别为小波分解的低频信号和高频信号。

图6 技术路线图

2.1 小波分析

为从时频角度揭示对旋风机内部的失速流动的特征，借助小波变换来分析失速发生时流场内的非定常静压信号。信号的小波变换表达式为：

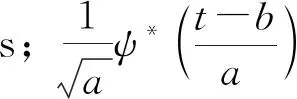
小波分析法的最大优点是使用时间分辨率随频率变化的时间窗口，即当处理低频信号时，时间窗口比较大，而当处理高频信号时，时间窗口比较小。失稳信号一般都包含在压力信号的低频段，使用小波分析法刚好能够提取出详细的失稳信息。另外，避免了傅里叶变换在时域和频域完全分离的缺陷，联合时域和频域来分析信号，能同时考虑时域和频域的特征。

2.2 频域分析

对图3中A点的压力脉动数据(15个旋转周期)进行信号分析处理，时域波形如图7所示。对压力信号做FFT得到如图8所示的频谱。

图7 原始信号的时域波形

图8 原始信号的频谱图

由图8可以看出，信号频率主要集中在600Hz以内，有两个非常明显的频率分量即70Hz和555Hz，幅值都比较大，同时还包括140Hz等频率分量，但幅值都较小。555Hz为两倍后级叶片通过频率(BPF=980/60×17=227.6Hz)，70Hz属于低频分量且推测为失速的特征频率。但是，由于长度为15个旋转周期的信号包含了风机稳态和非稳态的信号频率，而信号的FFT处理是针对信号的整体进行全局变换得到的频域信息。因此需要对信号在时域上进行划分，基于短时傅里叶变换的思路，把原始的15个旋转周期长度的信号每3个旋转周期分为一段即a段(5T—8T)、b段(8T—11T)、c段(11T—14T)、d段(14T—17T)、e段(17T—20T)，然后对每一段进行FFT处理，这样可以得到5幅3个旋转周期长度的信号频谱图，如图9所示。由图9可知风机在失速状态下的时域、频域特征，555Hz频率分量始终存在，且幅值保持不变。在b段开始出现70Hz及140Hz等频率分量，随着时间增加幅值逐渐增大。总体来看，对旋风机失速特征表现为70Hz及140Hz等频率分量的出现。

图9 A点压力信号的FFT分析

2.3 小波-时频分析

由上述频谱分析确定了风机进入失速状态时频率的主要成分和幅值变化。虽然上述分段频谱分析将风机信号的失速突变时间缩小在3个旋转周期内，但本质上仍然是一段时域内的全部信息。因此，需要通过更加精细的划分来对风机内部的突变信号进行分析。Db(Daubechies，Db)小波对信号的局部奇异变化非常敏感，因此，本文采用Db小波作为基小波对信号进行多分辨分析。分析包含信号主要频率成分的低频部分，观察信号在失速前后的频率和幅值变化。

取失速前后7个旋转周期(6T—13T)的数据进行时频分析，原始信号的时域波形如图10所示。选用Db3小波对信号进行分析，采样频率为3333Hz(本文所用信号来自于数值模拟，因此文中的采样频率与数值模拟中的时间步长有关，为时间步长的倒数即f=1/T。本文数值模拟中的时间步长T=0.0003s，所以采样频率f=3333Hz)，进行4层小波分解。由上文可知：风机失速突变信号的主要特征为70Hz频率及140Hz等频率分量的出现，而第4层低频系数的频带范围是0～208.3125Hz，包含了失速流动的特征频率，因此将ca4低频系数进行单支重构得到只包含失速特征频率的信号分量，如图11所示。由图11可知，风机大约在10个旋转周期后压力开始下降(如红色标记)，进入失速状态，其与图4分析结果一致。

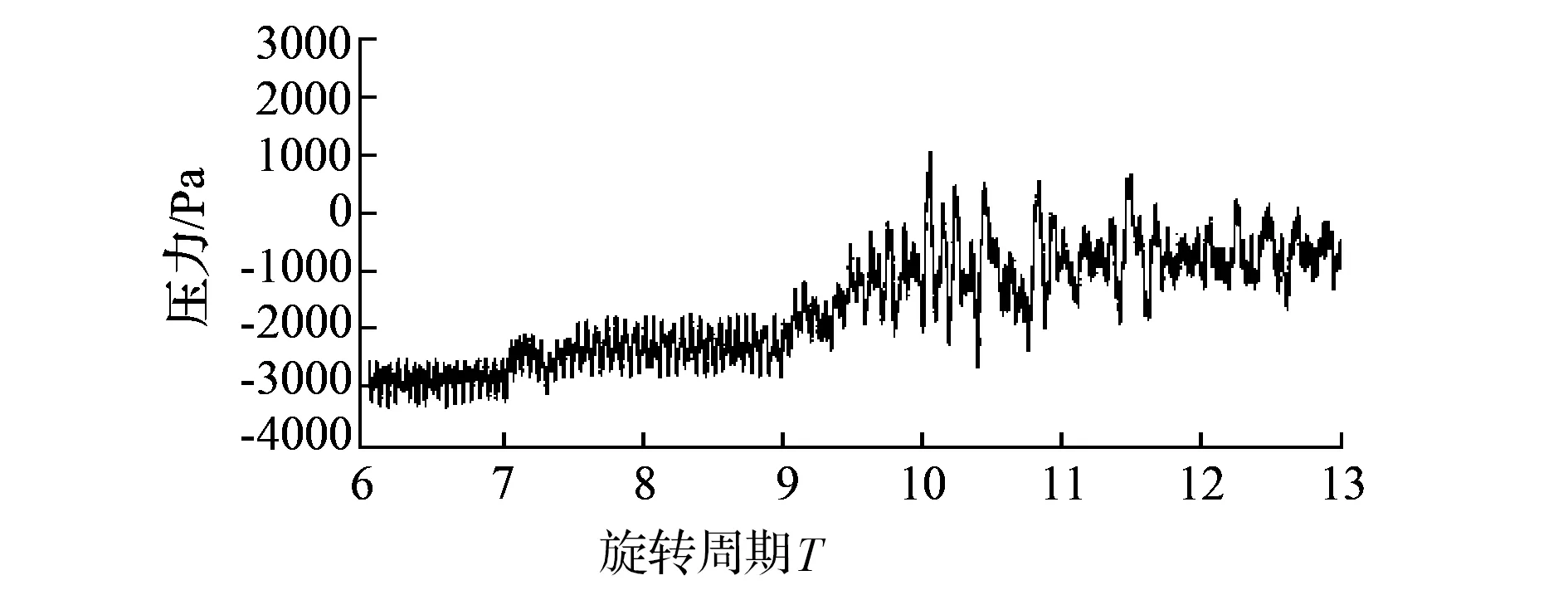
图10 原始信号的时域波形

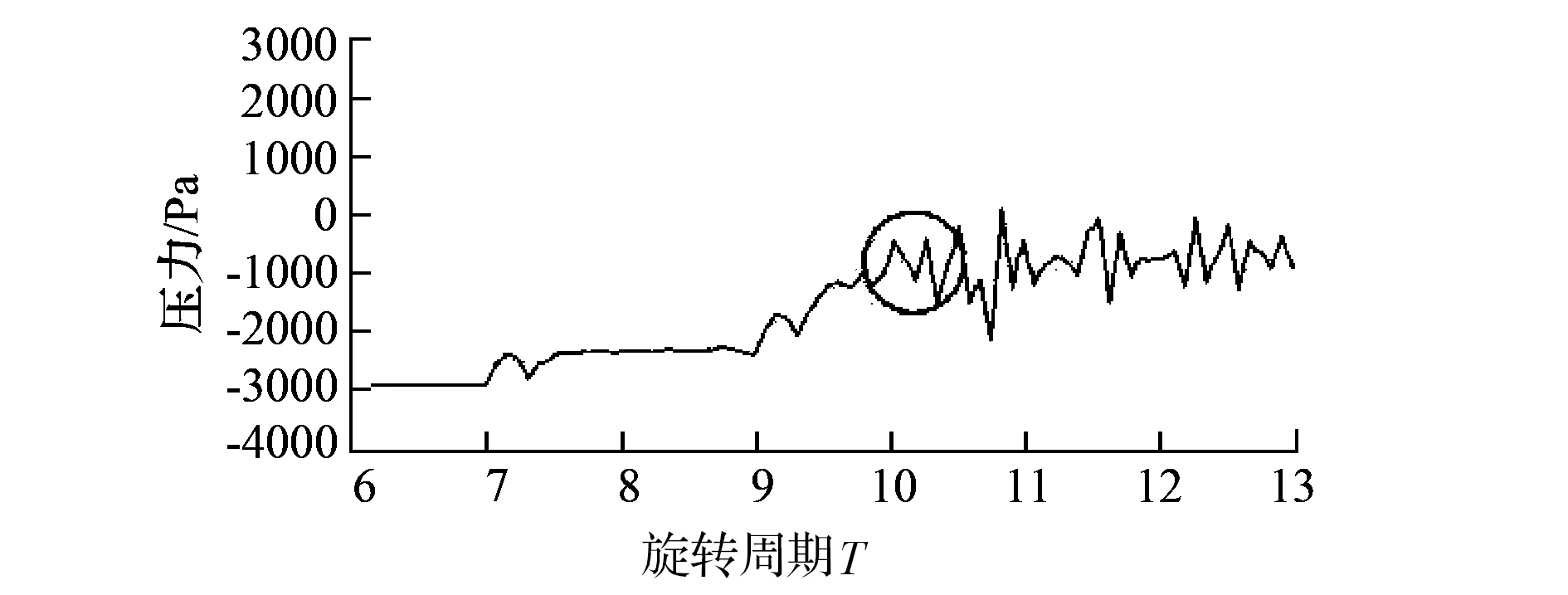
图11 ca4低频系数重构信号

为从时频角度揭示失速流动信号的特征，对图11所示的压力信号进行时频分析，如图12所示，横坐标以叶轮一个旋转周期为单位，纵坐标为频率，其颜色由蓝到黄代表小波变换系数由小到大。由图12可知，风机大约在第10个旋转周期开始出现一条70Hz频率带(如圈1所示)，同时伴随着140Hz频率分量的出现(如圈2所示)，但70Hz频率分量较140Hz频率分量明显。总体来看，频率分布趋势与图8所示频谱一致(70Hz幅值较大，140Hz幅值较小)，失速特征表现与图9分析结果一致(70Hz及140Hz频率分量的出现)，进入失速状态的时间与图4分析结果一致(大约在10个旋转周期后进入失速状态)。

图12 小波变换的时间频图

3 结 论

1)对旋风机在第10个旋转周期后进入失速状态，伴随着前缘溢流与尾缘反流的出现而发生。

2)通过分段频谱分析可以获得流动信号在时域上的变化，缩小了失速信号突变的时间范围，并从频域角度确定出失速特征表现为70Hz及140Hz频率分量的出现(失速下的频率是由失速团引起的，而失速团的形成与演变机理十分复杂，针对不同研究对象，失速团的个数也不尽相同，但与风机的结构、转速息息相关。一般来讲，失速团的个数少则2、3个，多则聚集于叶轮叶顶区域与叶片数相同，失速团的转速一般为30%～70%转子转速。)。

3)利用小波-时频分析方法从时频角度进行失速流动特征分析，发现对旋风机在第10个旋转周期开始出现一条70Hz频率带，同时伴随着140Hz频率带的出现，但70Hz频率分量较140Hz频率分量明显。

4)采用FFT技术与小波-时频分析相结合的方法，可有效捕捉对旋风机失速流动现象的瞬态时频特征，能够确定失速特征及失速时间。