基于灰色模型快速预测亚麻纤维力学性能
2022-03-22管丽媛王国和
管丽媛, 王 钟,b, 王国和,b,c, 李 辛, 祁 宁,b
(苏州大学 a.纺织与服装工程学院;b.现代丝绸国家工程实验室;c.纺织行业天然染料重点实验室,江苏 苏州 215123)
0 引 言
麻纤维主要成分为纤维素和非纤维素类物质。然而,半纤维素、果胶和木质素等非纤维素类物质与麻纤维力学性能之间的关联及其影响效果,目前依然缺少相关定论。
在对变量间潜在规律的探索中,以灰色系统理论为基础的灰色模型可有效地从表面无规律、不明确的小样本数据系统中推断出各信息间的关联程度,进而实现对各变量进行系统地分析和精确预测。灰色模型也因其预测结果精确度高、建模所需数据少且数据可无序等优点得到迅速发展[1]。Tangkuma 等[2]建立灰色模型用于在最终故障发生之前预测机器的退化;Wang等[3]提出一种改进的多元灰色模型(IMGM)用于对电池的健康状态进行预测和诊断,该模型可有效提高储能技术的可靠性;Xiao 等[4]应用交通流动力学理论中的车辆守恒原理,建立了道路交通流的灰色模型,用于短期交通流的预测;Ye 等[5]提出采用灰色模型来衡量中国交通运输业的CO2排放量,测算各因素对碳排放的累积影响,其预测结果对制定相应的政策具有重要意义。然而在纺织领域的相关研究主要集中在运用灰关联分析探究各因素之间的影响程度,戎佳琦等[6]计算分析出亚麻粗纱煮漂后各主要化学成分对细纱强力的影响程度;王春红等[7]探究了黄麻部分成分含量与力学性能间的灰色关联度。两项研究均表明了各成分对性能影响程度,但各成分对性能的具体影响效果尚未进行探究。
鉴于以上原因,本文以亚麻纤维为原料,基于灰色系统建模理论,以化学脱胶法测定各成分含量,分别建立以成分含量为依据的纤维断裂伸长率、细度和断裂强度的灰色预测模型。探究各成分含量对力学性能的影响效果,实现快速、准确地预测纤维力学性能,为评判亚麻纤维能否较好地用于纺纱提供理论基础,方便在实际工业生产中纺纱用纤维的选用。
1 构建灰色模型
1.1 灰色模型参数定义
灰色模型可表示为GM(x,y),其中x 为模型计算采用的阶次,y 为模型中包含的变量数。目前常用一阶多变量灰色模型GM(1,y)研究变量间的潜在规律,本文通过建立GM(1,5)模型探究亚麻纤维化学成分含量与其力学性能间的关联。将各样品的纤维素、半纤维素、果胶和木质素含量构成的序列作为比较数列,分别记为X1
(m)(k)~X4(m)(k),其中m =0 时表示初始化处理数据,m =1 时表示1 次累加生成数据,k 为序列数。将断裂伸长率、细度、断裂强度作为参考数列,分别记为X5
(m)(k)~X7(m)(k)。模型的灰微分方程可定义为[8]
式中:b1~b4为灰作用量;a为发展系数;Z1(k)为均值生成数据。
1.2 灰色模型建模过程
为减少数据的离散性,对样品的各成分含量和力学性能数值进行初始化处理,即[8]:
对初始化处理数据进行处理,可得累加生成数列和均值生成数列[9]:
通过均值生成数列和累加生成数列得到矩阵B和向量Yi[8]:
本文运用Matlab 9.0 仿真软件进行编程运算,求得发展系数a和灰作用量b1~b4[10]:
2 实验部分
2.1 材料与仪器
(1)原料。亚麻纤维,江苏楼尼伽进出口有限公司进口产于荷兰。
(2)试剂。无水氯化钙(96%)、氢氧化钠(96%)、亚氯酸钠(80%)、石油醚(分析纯),国药集团化学试剂苏州有限公司;过氧化氢(30%)、硫酸(分析纯),苏大实验材料供应中心;氯化钡(99%)、草酸铵(99.8%),上海百灵威化学技术有限公司。
(3)仪器。INSTRON-3365 材料试验机,英斯特姆公司;Y171 型纤维切断器,常州德普纺织科技有限公司;ES-J 电子分析天平,厦门莱斯德科学仪器有限公司;FCD-10 无油真空泵,上海启前电子科技有限公司;500 mL玻璃砂芯过滤装置,北京奥秘佳得医药科技有限公司;DHG-9036A 电热恒温鼓风干燥箱,上海精宏实验设备有限公司。
2.2 测试用亚麻纤维样品的制备
在浴比1∶25 条件下,以NaOH浓度、NaClO2浓度、H2O2浓度、时间和温度为试验因素,通过正交设计得到16 组纤维化学脱胶处理实验方案。L16(45)因素水平表如表1 所示(表中A、B 和C 分别代表NaOH、NaClO2和H2O2,下同)。
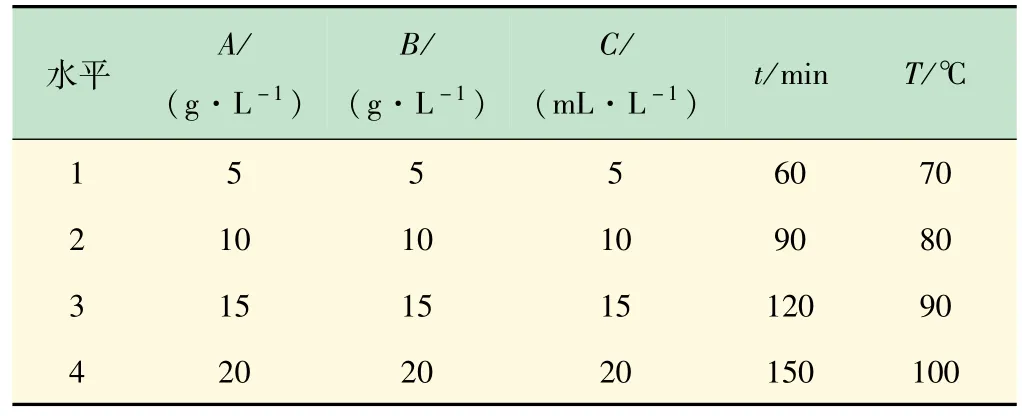
表1 L16(45)因素水平表
2.3 化学成分测定
本文按GB/T 5889—1986《苎麻化学成分定量分析方法》测定样品各化学成分的含量。其中,以石油醚代替苯乙醇测定脂蜡质的含量,重复测定3 次取平均值。
2.4 力学性能测试
(1)断裂伸长率。按GB/T 14337—2008《化学纤维短纤维拉伸性能试验方法》,采用INSTRON-3365材料试验机测量各样品的断裂伸长率。拉伸速度为10 mm/min,夹持距离为10 mm。各样品均测试30 次取平均值。
(2)细度。依据中段切断称重法,在恒温恒湿条件下对纤维进行预调湿和梳理,并采用Y171 型纤维切断器将亚麻纤维束切成长度为0.01 m的短纤维,称重并计算根数。纤维细度的计算[11]:
式中:Ndt为线密度,dtex;Gk为纤维质量,g;n为纤维根数;L为纤维长度,m。
(3)断裂强度。纤维断裂强度的计算[12]:
式中:FT为断裂强度,cN/dtex;为平均断裂强力,cN。
3 结果与讨论
3.1 化学成分及力学性能测试
由表2 各亚麻纤维样品成分含量和力学性能的测试结果可知,各样品成分含量随处理程度的不同而存在差异,纤维的断裂伸长率、细度和断裂强度也存在相应的区别,表明亚麻纤维各成分含量对其力学性能有一定的影响,但影响规律是未知的。
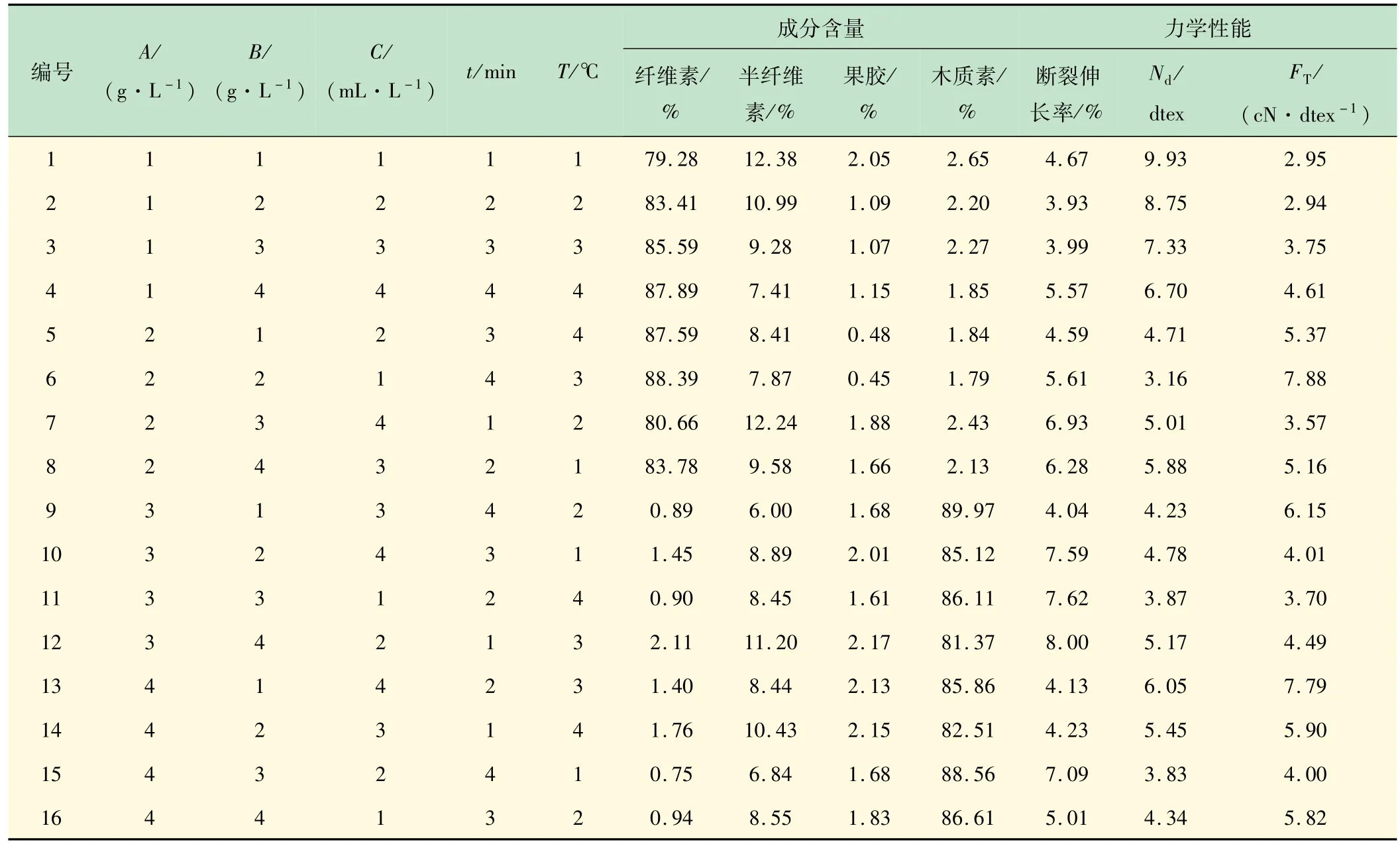
表2 各亚麻纤维样品成分含量和力学性能测试结果
3.2 GM(1,5)模型分析
以纤维的断裂伸长率为例,建立GM1(1,5)灰色模型,探讨亚麻纤维各成分含量对断裂伸长率的影响规律。依次根据式(2)~(6)分别求得矩阵B 和向量Yi,进而根据式(7)计算可得:
将上述计算得到的a 和b1~b4代入式(1),得到亚麻纤维纤维素、半纤维素、果胶和木质素含量与其断裂伸长率的GM1(1,5)灰色模型:
由式(10)可知,灰作用量b1和b3为负值,表明其对X(0)5(k)的增大有阻碍作用;b2和b4为正值,对X(0)5(k)的增大有积极作用。因此亚麻纤维纤维素、果胶含量的增加会抑制断裂伸长率的增大,而半纤维素、木质素含量的增加会促进断裂伸长率的增大。这一结果与理论分析相符合,纤维素作为植物外层细胞壁主要物质,是承受外力作用的主体,从而对刚性起决定性作用[13]。而半纤维素是植物初生壁的主要物质成分,与伸展蛋白等成分组成具有一定弹性的细胞壁,因此其含量的增加有利于纤维断裂伸长率的增大。
同理,得到亚麻纤维纤维素、半纤维素、果胶和木质素含量与其细度的GM2(1,5)灰色模型:
由式(11)可知,b1和b3为负值,表明亚麻纤维纤维素、果胶会抑制线密度的增大;b2和b4为正值,半纤维素、木质素对线密度的增大有促进作用。因此半纤维素和木质素的含量越高,纤维直径越大;纤维素和果胶的含量越高,纤维直径越小。
同理,得到亚麻纤维纤维素、半纤维素、果胶和木质素含量与其断裂强度的GM3(1,5)灰色模型:
由式(12)可知,b1和b4为正值,即纤维素和木质素含量的增加能够促进断裂强度的增大;b2和b3为负值,即半纤维素、果胶含量的增加会抑制断裂强度的增大。此处与其他学者研究的结论一致[14]。纤维素是一种没有分支的线性(结晶)分子[15],其分子链间具有较强的相互作用力。以及木质素是一种复杂的、非晶态的三维酚醛树脂网络[16],是构建植物骨架无法缺少的主要成分之一,对纤维素、半纤维素等物质成分起到接结作用,从而使纤维具有承载外界机械力的能力。因此其含量的增加有利于纤维断裂强度的增大。
3.3 GM(1,5)模型误差检验
为验证模型预测结果的准确性,对建立的各灰色模型进行误差分析[8]:
由式(13)计算各断裂伸长率GM1(1,5)、GM2(1,5)和GM3(1,5)模型对应的平均误差δ1、δ2和δ3分别为0.11、0.16 和0.34。模型预测值与实测值之间的误差均在可接受范围内,表明3 个灰色模型的预测精度均较高。即建立的模型具备较高的可靠性,可用于快速、准确地预测亚麻纤维的力学性能。
4 结 语
本文成功建立了亚麻纤维各成分含量与断裂伸长率、细度和断裂强度的灰色模型,探究各成分含量对力学性能影响效果的基础上,实现了快速、准确地预测亚麻纤维的力学性能。通过正交试验设计及测试取得的模型表明,亚麻纤维的断裂伸长率和细度随半纤维素、木质素含量的增加而增大,随纤维素、果胶含量的增加而降低;断裂强度随纤维素、木质素含量的增加而提高,随半纤维素、果胶含量的增加而降低。误差检验表明各模型预测结果较为准确,本文的模型为评判亚麻纤维能否较好地用于纺纱提供了理论基础,方便在实际应用中纺纱用纤维的选用。
