基于稀疏化卷积网络剪枝的图像识别方法研究
2022-03-22叶汉民李志波程小辉周颖慧
叶汉民, 李志波, 程小辉, 周颖慧
(桂林理工大学信息科学与工程学院;广西嵌入式技术与智能系统重点实验室,广西 桂林 541004)
0 引 言
目前,深度神经网络[1]以自动学习目标深度特征、模型泛化能力强等诸多优点成为工业界及学术界的热点研究领域,同时带来了神经网络在时间和空间复杂度上导致的计算资源紧张问题,进一步制约先进神经网络模型在有限计算资源条件下的应用扩展。网络通过压缩与加速可以将先进的神经网络模型部署于嵌入式系统或便携式设备,摆脱对存储和计算资源的硬性要求,推广深度神经网络的应用领域[2]。因此如何保证模型精确度前提下使得计算资源最小化是深度神经网络压缩的关键问题。
网络剪枝能够在获得较大的压缩比的同时对网络中的精度影响较小,加速模型推理运算性能,有效减少模型计算存储的内存消耗。现有对网络剪枝开展的研究包含:对于非结构化剪枝而言,Han等[3]首次提出训练-剪枝-微调经典剪枝策略,但通过该方式带来额外的计算及训练时间代价。Blalock 等[4]以剪枝后的梯度范数为准则,对剪枝后梯度范数减少最少的权重进行剪枝,并提出标准化基准指标,防止陷入对比剪枝方法时的常见误区。Chen等[5]利用深度强化学习技术,结合动态剪枝信息及静态剪枝信息,通过减少动态剪枝的存储空间需求,解决平衡动态灵活性和存储空间的矛盾。Molchanov等[6]通过泰勒分解理论化来移除对损失影响的参数,利用反向传播梯度的度量来解决在不损坏网络时对哪些参数进行修剪;在进行全局及局部剪枝时,Li等[7]考虑到所选标准能够应用于网络架构中所有的参数或过滤器,采用逐层局部剪枝方法时可以避免层崩溃现象,得到更好的剪枝效果,但时间开销成本较大。
综合以上研究,本文在非结构剪枝结构下进行稀疏性训练,在进行网络初始化引入随机掩码,计算和保留贡献程度较大的权重参数,通过动态更新网络中掩码分布及权重数量完成模型参数遍历,将得到的精简网络模型基于公共数据集CIFAR10/100 进行剪枝方法性能测试。
1 基本原理和设计思路
1.1 结构化剪枝
基于幅值权重剪枝[8]并没有减小网络计算成本,而是通过剔除对于对结果影响精度较小的卷积核,将网络的这些影响较小的卷积核以及特征图进行一并移除,在减少计算成本的同时避免产生稀疏连接结构。利用稀疏化尺度因子[9]进行网络剪枝,主要通过批量规范化层缩放因子γ 衡量不同通道的必要性,移除对结果贡献度较小的通道,加速网络参数运算,实现网络架构的精简。通过结构化学习思想[10]可以有效规范参数最大可能稀疏,使用网络权重以组的方式调制到零附近,实现学习参数结构化稀疏,进行网络推理的加速。当网络剪枝在不依赖于训练数据时[11],采用相同数量卷积单元过滤器及其对应卷积层进行剪枝,将分值低的卷积单元进行过滤,通过结构化剪枝去除卷积滤波器及内核,可以直接对神经网络加速并部署,但应对比改变网络层次的输入所导致输出维度的差异。
1.2 非结构化剪枝
近年来,在不影响性能情况下能够进行大量剪枝连接,最精细粒度可以对卷积核内参数修剪,剪枝权重不受约束限制,但大多数网络处理架构及硬件无法对稀疏矩阵运算进行加速处理。彩票假设[12]揭示随机初始化网络架构中存在的一个经单独训练可达到与原网络在同等条件下性能相似的精简网络,可以通过保留原网络初始化权重进行训练,确定最小权重位置,创建相应的剪枝掩码,随后使用初始化权重进行网络初始化,按照得到的掩码进行修剪,并通过实验证明了修剪发现的中奖彩票网络架构比原始网络学习能力更强,能够达到更高准确度和泛化能力。为避免产生额外训练时间开销,将权重的连接敏感度[13]作为是否剪枝的评判标准,利用损失函数及连接敏感度的梯度进行剪枝,随后对剪枝的网络进行再训练,移除不重要的连接,节省了剪枝-微调迭代周期。此外,为避免梯度传递出现问题,采用迭代突触流剪枝思想[14]有效解决网络崩塌及过早剪枝导致网络不可训练等问题,该方法在不需要额外数据样本支撑时持平或超越软剪枝测试性能。
1.3 研究思路与模型基础
本文使用Data ={xi,yi}ni=1表示训练数据集合,xi、yi分别为神经网络中训练的标签和样本原始标签,n为样本数量。由于本文在CIFAR10/100 数据集在进行算法验证,网络初始化定义为具有H 层的神经网络用于分类任务T。其中:wH(wH∈RmH)表示第H 层中的权重值;mH代表第H 层中的权重数量;f(W1,W2,W3,…,WH;x)为网络输入。分类目标则是在网络和目标标签的输出上使得误差函数最小化,即l(f(W1,W2,…,WH;xi),yi),通过不断优化误差函数来加速模型收敛速度,并在测试数据集上进行性能测试,以获得最佳网络精简模型。
在开展神经网络的剪枝研究中,其背后假设神经网络通常是过度参数化的,可通过一个参数量更少的网络获得相似性能,在空间、时间、效率及应用等方面资源利用达到最大合理化。通过设定数据集Data 及稀疏度k等变量,网络剪枝可写成以下约束优化[13]问题,即:
式中:l(·)为损失函数;w为网络参数;m为网络参数数量总和为标准L0 范数。
在进行优化目标问题时,通常采取增加稀疏性惩罚措施。对于结果稀疏性而言,需要迭代调整超参数才能获得较好性能。此外,可以将上述问题转化为通过某种策略移除网络架构中冗余参数或连接方式,冗余连接可定义为
式中:si为显著性程度;w(i)为网络权重;Hii为海森矩阵值
本文在开展剪枝实验时,对于每个稀疏连接层,在经历一轮训练时,利用随机掩码(0,1)进行网络初始化,修剪部分接近零的最低权重,随后增加新的随机权重替换已被修剪过的权重,迭代执行修剪移除权重与增加随机权重的过程进行网络训练。通过线性缩放权重比例遍历网络,实现网络模型稀疏训练。在网络剪枝训练中,掩码的初始化设置是随机的,逐渐对其进行调整,同时在网络中各层之间保持相同的稀疏级别。其基本流程:①利用随机掩码初始化神经网络模型;②设置网络层的权重保留比例,计算并保存网络指定稀疏度的权重③剔除相对较小且接近0 的权重,增加同等数量随机权重进行网络训练与更新;④线性缩放权重保留比例并遍历网络中所有参数,最终保存权重数量等同于②中权重数量;⑤迭代执行流程③~④,最终获得精简剪枝模型。
本实验使用随机梯度下降作为梯度优化器,为保证网络训练高效性,所以在架构中引进批量规范化层(Batch-Normalization,BN)层。在训练过程当中,BN层[9]能够计算不同批次样本数据的平均值及方差,改善梯度在网络中的传递,加速训练过程的收敛,即:
式中:x(i)是小批量样本中第i条数据;μβ、σ2β分别为样本均值和方差;mβ为小批量的数值。通过零均值及标准化的x^(i)为
为避免分母出现零的情况发生,使网络输出结果存在意义,采用ε 进行平滑,一般取值为ε =0.001。通过BN处理后的输出为
式中,γ、β是网络结构特征图的学习参数。
2 实验分析
本文结合稀疏性剪枝策略对深度神经网络进行剪枝,并实验验证其实用性。实验使用公共数据集CIFAR10[15]与CIFAR100[16]作为实验对象,本文基于稀疏化卷积网络进行非结构化剪枝方法实验,设置对比方法包含:文献[12]中在基于幅值的剪枝模式进行权重初始化,揭示稀疏架构和初始化联合训练机制;文献[13]是基于网络初始化进行修剪优化,利用深度网络的连接模板来反馈权重重要性;文献[14]中通过保持梯度流在训练前挑选最精简的网络结构,这些方法都和随机初始化网络进行稀疏训练有一定联系,因此后续测试主要与这些方法进行对比。采用Pytorch 软件深度学习框架进行网络剪枝训练,在配置为NVIDIA RTX 1080Ti,显存11G的GPU云平台上运算。
2.1 实验数据及评估指标
本实验基于CIFAR10/100 数据集进行算法验证,该数据集可以直观反馈剪枝方法的时效性。CIFAR10/100 数据集由Alex Krizhevsky 等人收集而来,CIFAR10 中样本总量达60 000 个,可以划分为10个类别,每类中包含6 000 个样本,每张样本尺寸大小为32 ×32。CIFAR100 则包含100 个类别,样本尺寸及总数量与CIFAR10 保持一致。选取经典的VGG 和ResNet作为待剪枝网络,其中VGG网络作为没有跨层连接网络架构代表,而ResNet作为跨层连接网络架构代表,能够有效反映网络压缩对于网络模型的效果。实验通过测试剪枝后模型的准确率、剪枝比率、参数量进行与其他算法对比。其中准确率反映的是剪枝后网络在数据集测试中Top-1 的分类效果。剪枝比率分别设置为90%、95%和98%进行实验对比。参数量则反映网络模型使用内存大小,通过减少模型参数量提高模型的压缩效率。
2.2 超参数设定
本文在数据集CIFAR10/100 上进行训练时,单个训练batch设置为64,单个测试batch 设置为50,累计训练160 轮epoch;初始学习率为0.1。为更好地使模型收敛更快,性能测试达到最佳,在训练总进度达到50%、75%时分别对学习率进行衰减调整,衰减后的学习速率设置为之前学习率的0.1 倍。在整个迭代剪枝训练过程中,首先采用Kaiming方法进行初始化,利用随机梯度下降方法优化梯度在架构中的传递,动量参数设置为0.9,衰退因子设置为0.000 1。
2.3 基于ResNet-32网络在CIFAR10/100的剪枝实验
表1 为在CIFAR10/100 数据集上对ResNet-32 网络架构中进行修剪并对比实验结果。为了确保不同算法实验数据的精确度,分别在相同实验环境进行对比。实验在本文配置的云平台网络设备条件下进行运算,单次训练及测试时间约为1.5 h。在未对ResNet-32网络架构进行剪枝操作时,CIFAR10/100 基线的测试准确度分别为93.09%和74.54%。基于ResNet-32 架构分别进行90%、95%、98%剪枝操作后,卷积层和线性层参数量总和分别为0.19、0.1、0.05MB,参数量在一定程度上进行了大批量的剔除。为了更直观地对比不同方法在剪枝过程中精度变化情况,选取具有代表性的3张基于ResNet-32架构方法实验图,如图1所示。
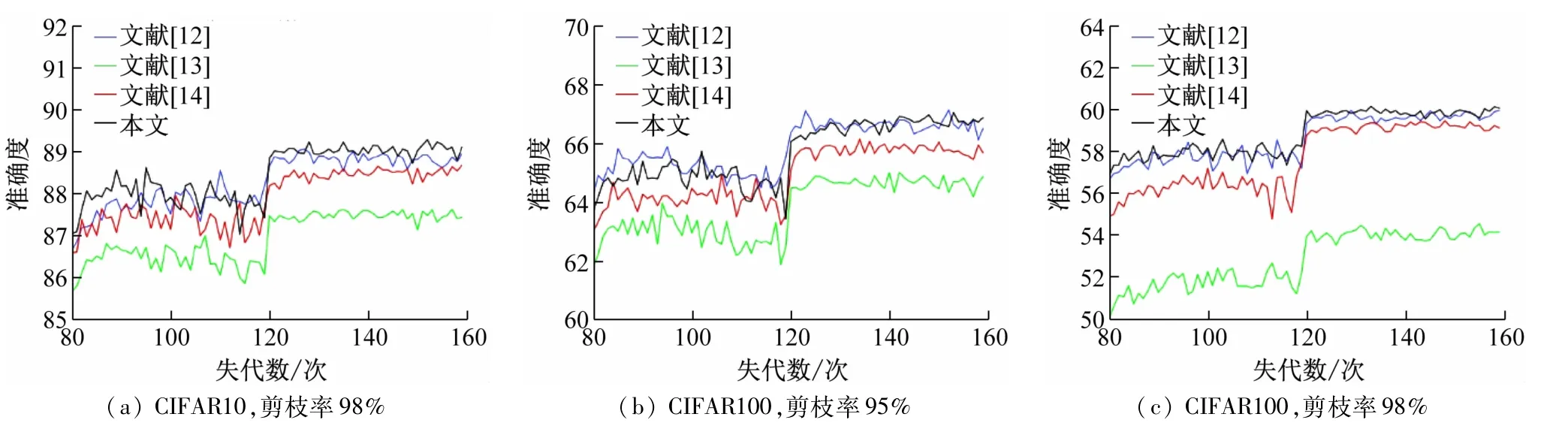
图1 两个数据集不同剪枝率训练效果对比
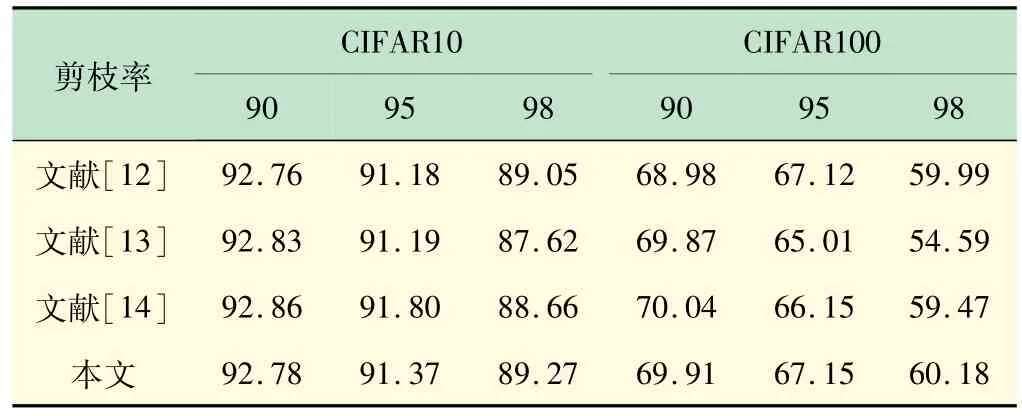
表1 在CIFAR10/100 上基于ResNet-32 架构方法对比实验%
在修剪ResNet-32 模型使其减少相当参数量时,CIFAR10/100 数据集上识别结果表明:
(1)CIFAR10 数据集。当在大剪枝比率98%的测试下,本文方法基于CIFAR10 数据集上的识别准确度为89.27%,分别比文献[13-14]中提高1.65%、比文献[14]中提高0.61%,比文献[12]中精度提升0.22%。文献[12]中采用基于剪枝寻找最佳网络架构的策略对网络学习率敏感度较高,如果学习率选取不当易导致模型训练出现振荡问题,故需要在训练开始时设定较小的学习率,待模型对数据的适应程度较好时采用预先设定的学习率进行剪枝训练,避免精度出现较大程度衰退。方法对比实验基于CIFAR10 数据集识别性能相当时,而面向较为复杂数据集CIFAR100时,本文方法对比其他方法在识别精度上有明显提升。
(2)CIFAR100 数据集。当网络设置较大剪枝率98%时,剔除网络中大量冗余参数时,本文方法图像识别精度达到60.18%,分别比文献[12-13]中精度提高0.19%、5.59%,比文献[14]中准确度上升0.71%,而当剪枝率为95%时,本文算法虽在CIFAR10 数据集上较文献[14]中算法准确度降低了0.43%,但在CIFAR100 数据集上的识别精度提高1.00%。当剪枝率为90%时,本文方法基于CIFIA10 数据集上较其他方法的测试准确度相当,但在CIFAR100 数据集上的识别精度优于文献[12-13]中的算法性能。在层内保持比率下降的趋势下,一些特殊层中的保持比率不尽相同,ResNet-32 网络架构中下采样层的保持比率要高于它的相邻层。
2.4 在CIFAR10/100 基于VGG19 网络架构的剪枝实验
表2 为在基于CIFAR10/100 数据集在VGG19 网络模型开展对比实验结果。为了确保不同算法实验数据的精准度,分别在同等实验环境下进行算法性能的测试。实验首先在未剪枝的条件下基于VGG-19 模型进行识别,其次再进行不同剪枝比例条件下的精度识别测试。实验在本文配置的云平台网络设备条件下进行运算,网络模型进行单次训练及测试时间约为1.5 h。在未对VGG-19 网络架构进行剪枝操作时,在数据集CIFAR10/100 上基线测试准确度分别为93.91%和72.85%。基于VGG-19 架构分别进行剪枝率90%、95%、98%操作后,卷积层和线性层参数量总和分别为2.01、1.02、0.41MB。为更直观地观察不同方法在剪枝过程中精度变化情况,选取代表性的3 张基于VGG-19 架构的方法对比测试图,如图2 所示。
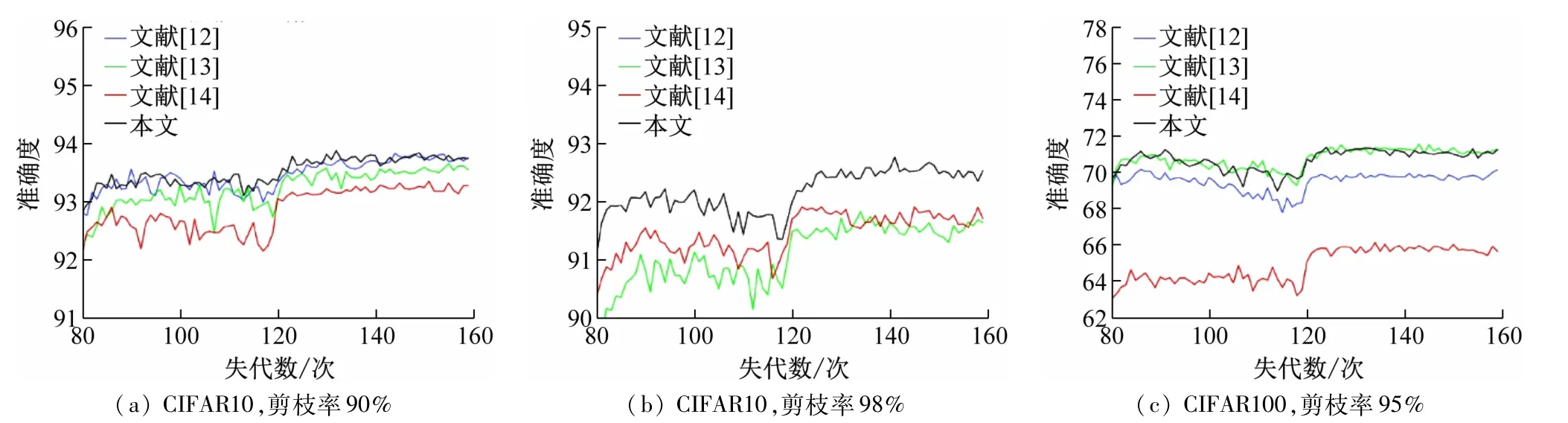
图2 不同数据集剪枝比例效果对比

表2 在CIFAR10/100上基于VGG19网络架构方法对比实验%
在修剪VGG-19 模型使其减少相当参数量时,有效剔除模型中冗余参数,得到精简网络模型。根据CIFAR10/100 数据集上精度测试表明:
(1)CIFAR10 数据集。当网络剪枝率分别设定为90%、95%和98%时,本文方法识别精度分为达到93.87%、93.38%和92.76%,对比方法在CIFAR10 数据集上识别精度相当,文献[12]中方法在较大剪枝率98%基于CIFAR10的准确率仅为10.00%,准确度出现显著下降,表明该方法在剔除大规模的参数时出现某些层保留很少权重的现象,导致网络性能出现退化。在较大剪枝率98%条件测试下,本文方法在目标数据集上识别精度为92.76%,比文献[14]中对应数据集上提高0.85%。
(2)CIFAR100 数据集。本文方法基于CIFAR100数据集进行模型测试时,剪枝率依次设置为90%、95%和98%时,模型识别精度达到69.91%、71.37%和69.14%。当剪枝率为95%时,模型识别精度分别比算法[12-14]分别提高1.22%、0.11%和5.22%,文献[13]中采用权重连接衡量策略进行剪枝,通过计算损失函数与权重关联梯度对权重置零,但基于CIFAR100数据集进行大剪枝率时,准确度出现骤减情况,在一定程度上说明在高剪枝率的条件下基于多目标识别易出现误差。本文方法基于网络架构的测试中发现VGG的衰减速率明显低于ResNet架构,准确度不会出现骤减现象,说明网络中权重分布较为均衡,梯度流在网络中传播趋于稳定。
3 结 语
本文采用初始化剪枝方式,不需要单独对待剪枝网络进行预训练,通过迭代更新训练中掩码及权重参数得出精简网络结构,网络运算量和参数量得到大幅度减少。通过在不同数据集及不同网络架构中的性能测试,对比其他剪枝网络性能测试结果表明:①本文方法在同等实验条件下剪枝率逐渐提高时模型精度不会出现骤减现象;②基于VGG 与ResNet 网络模型在相对较大剪枝率95%、98%条件设置下,模型准确度较其他经典算法有明显提高;③未来将对轻量级神经网络开展剪枝优化研究,同时融合知识蒸馏的相关策略和方法,得到更大程度压缩的网络模型。
