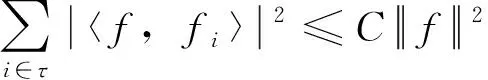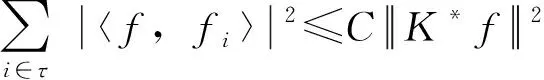K-g-框架的等价刻画和K-框架交织的擦除
2022-03-22肖祥春林泽平
肖祥春,林泽平
(厦门理工学院数学与统计学院,福建 厦门 361024)
1952年,Duffin等[1]提出了Hilbert空间H中的框架概念,当时并没有引起学者们的太多关注。直到1986年,由于Daubechies等[2]的突出性研究,框架理论[3-5]才被学者们广泛研究和关注。目前,框架理论已经被广泛应用于信号采样[6]、量子力学[7]、图像处理[8]、编码与信号传输[9]等领域。
K-框架是Gavruta等[10]为研究原子分解而提出的一种与Hilbert空间有界线性算子K有关的框架。由于K-框架含有有界线性算子K[11-12],Hilbert空间中的K-框架与经典的框架有很多的不同,如:对于经典框架而言,Hilbert空间中的元素序列{fi}i∈I构成经典框架等价于其合成算子是满的,而{fi}i∈I构成K-框架当且仅当其合成算子T是有界的,且满足R(K)⊂R(T)。随后K-框架在文献[13]又被进一步推广到K-g-框架[14-15]。
设{Λj:j∈J}为H关于{Vj:j∈J}的g-Bessel序列, {(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的fusion框架。 文献[16]用给定序列{Λj:j∈J}的导出序列{ujk}j∈J,k∈Kj来等价刻画{Λj:j∈J}成为一个g-框架。受此启发, 本文给出{Λj:j∈J}的另一种不同于文献[16]的新的导出序列{vjkπWjkΛj:j∈J,k∈Kj}, 并用它来等价刻画{Λj:j∈J}构成H的更一般的K-g-框架。特殊地, 若K=IH, 即可用{vjkπWjkΛj:j∈J,k∈Kj}来等价刻画{Λj:j∈J}构成H的g-框架。文献[17]讨论了Hilbert空间K-框架的交织的扰动和构造,而对K-框架交织的擦除却未涉及。本文在文献[17]的基础上进一步讨论K-框架交织的擦除性,得到一个含有2个独立参数的充分条件,使得在一对可K-交织的K-框架的基础上擦除若干元素后剩下的元素仍然可K-交织。虽然文献[18]也有讨论框架交织的擦除,但本文的擦除结论里条件更一般,含有2个独立参数。特殊地,若K=IH,即可得到文献[18]对应框架交织的擦除结论。
1 记号和预备知识
本文都采用如下的记号:H为一个可分Hilbert空间;若X、Y为Banach空间,记L(X,Y)表示从X到Y的有界线性算子的集合, 若X=Y, 则记为L(X),即L(X,X)=L(X);K:H→H是H上的有界线性算子,即K∈L(H);R(K)表示算子K的值域;J表示整数集的子集。
首先给出K-框架、K-g-框架、fusion框架和框架交织的定义和若干性质。
定义1[10]139设K∈L(H)。序列{fi}i∈I⊂H称为H的K-框架,如果存在常数A、B>0,使得
(1)
成立。 称满足式(1)的A、B为K-框架的下界和上界。 如果只有式(1)右边的不等式成立,则称{fi}i∈I为H的Bessel序列。
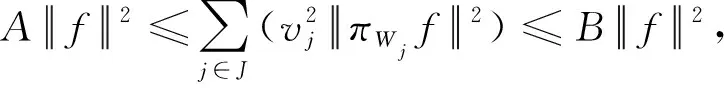
定义3[13]675设K∈L(H)。序列{Λj∈B(H,Vj):j∈J}称为H关于{Vj:j∈J}的K-g-框架,如果存在常数A、B>0,使得
(2)
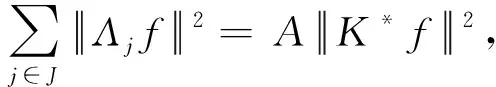
注1若有界线性算子K=IH,则K-框架和K-g-框架即为经典框架和g-框架。
下面回顾框架和K-框架的交织定义。
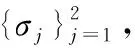
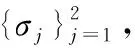
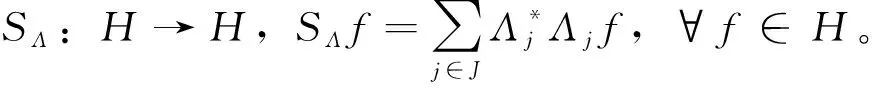
2 K-g-框架的等价刻画
首先用导出序列{vjkπWjkΛj}j∈J,k∈Kj来等价刻画{Λj:j∈J}为H中的K-g-框架,其中{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的fusion框架。
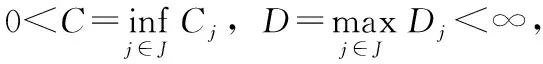
证明因为对任意的j∈J, {(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的界为Cj和Dj的fusion框架,有
(3)
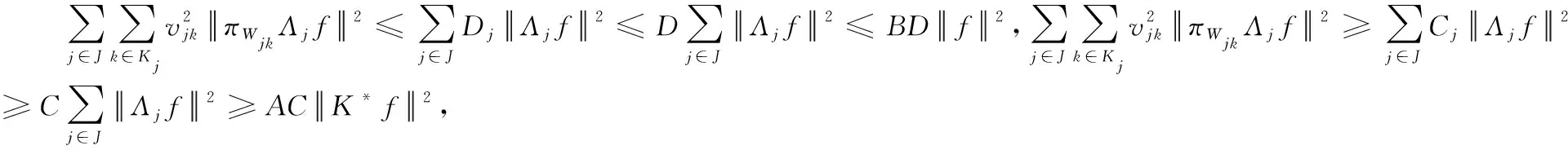
2)⟹1)。设{vjkπWjkΛj:j∈J,k∈Kj}为H关于{WjK:j∈J,k∈Kj}的K-g-框架,即有
(4)
对任意gj∈Vj,根据式(3)可知
(5)
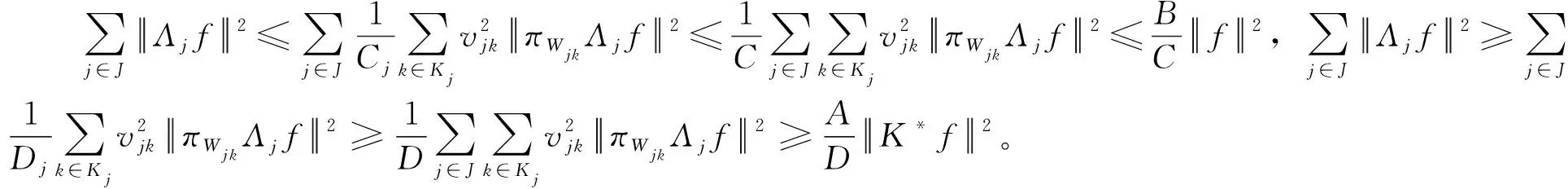
在定理1中,如果K=IH,则由定理1很容易得到文献[22]的推论2.3。
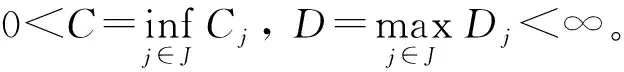
在定理1中,如果对任意的j∈J,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的Parseval fusion框架,则由定理1可进一步得到推论2。
推论2设{Λj:j∈J}为H关于{Vj:j∈J}的g-Bessel 序列,对任意j∈J,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的界为C的紧fusion框架。则下面的表述等价:1){Λj:j∈J}为H关于{Vj:j∈J}的界为A的紧K-g-框架;2){vjkπWjkΛj:j∈J,k∈Kj}为H关于{WjK:j∈J,k∈Kj}的界为AC的紧K-g-框架。
证明因为对任意的j∈J,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的界为A的紧fusion框架,所以有
(6)
又因为对任意的j∈J,f∈H,有Λjf∈Vj,结合式(6)可得
(7)
结论得证。
在推论2中,若对任意的j∈J,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的Parseval fusion框架,则进一步可得推论3。
推论3设{Λj:j∈J}为H关于{Vj:j∈J}的g-Bessel 序列,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的Parseval fusion框架。则下面的表述等价:1){Λj:j∈J}为H关于{Vj:j∈J}的界为A的紧K-g-框架; 2){vjkπWjkΛj:j∈J,k∈Kj}为H关于{WjK:j∈J,k∈Kj}的界为A的紧K-g-框架。
若对任意的j∈J, {(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的界为C的紧fusion框架,则可得{Λj:j∈J}和{(WjkΛj,vjk)}j∈J,k∈Kj的框架算子的关系。
命题1设{Λj:j∈J}为H关于{Vj:j∈J}的g-Bessel 序列,对任意j∈J,{(Wjk,vjk)}k∈Kj是Vj关于权重{vjk}k∈Kj的界为C的紧fusion框架,则有SWΛ=CSΛ,其中SWΛ为{vjkπWjkΛj:j∈J,k∈Kj}的框架算子。
证明根据式(7)可知,〈SWΛf,f〉=〈CSΛf,f〉, ∀f∈H, 即有〈(SWΛ-CSΛ)f,f〉=0。又因为f∈H是任意的,所以有SWΛ=CSΛ。
3 K-框架交织的擦除
接下来讨论K-框架的K-交织的擦除,即在一对可K-交织的K-框架的基础上擦除若干元素,使得剩下的元素仍然可K-交织。为此先给出引理1。
引理1设X、Y为Banach空间,Q∈L(X,Y)。若R(Q)是闭的,则存在Q的伪逆算子Q+:Y→X,满足
N(Q+)=R(Q)⊥,R(Q+)=N(Q)⊥,QQ+=IR(Q)。
(8)
特别地,如果有界线性算子Q可逆,则Q+=Q-1。
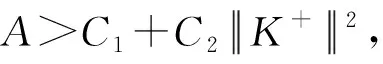
(9)
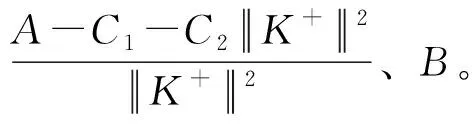
证明因为{fi}i∈I和{gi}i∈I在H中可K-交织,A、B为其统一框架界,所以对任意子集σ⊂I,有
(10)
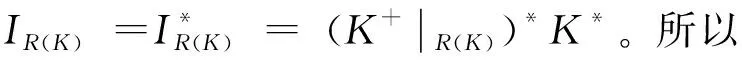
(11)
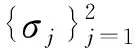
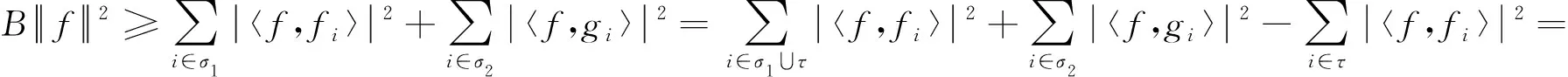
(12)
在式(12)中,若σ1=Iτ,则可知{fi}i∈Iτ为R(K)上的框架;若σ1=Ø,则可知{gi}i∈Iτ为R(K)上的框架。所以{fi}i∈Iτ和{gi}i∈Iτ在R(K)上可交织。
若在式(9)中分别令K=IH和C2=0,则由定理2可得到如下关于框架和K-框架擦除的2个推论。