海上“三高”气井井口抬升预测模型建立与应用

张涛，任松涛，梅明阳，康文泉，杨玉豪

(1.中海油能源发展股份有限公司工程技术湛江分公司，广东 湛江 524057；2.中海石油(中国)有限公司湛江分公司，广东 湛江 524057)

1 研究背景

目前南海西部某正开发的高温高压气田规模庞大。特征：(1)气藏温压高。实钻井底温度超150 ℃，最高压力系数1.85。(2)井深，井型复杂。开发井平均井深4 259.47 m，最大井深4 637 m，最长水平段513 m，主要以水平井、高井斜定向井为主。(3)气井配产高。该气田储层构造的物性好，多口井配产超100万立方米，最低60万立方米。(4)采取边钻完井边生产模式。该气田是国内海上首次采取边钻完井边生产模式的高温高压气田，钻完井作业期间安全风险把控难度大。前期各井在生产阶段都出现过明显的井口抬升现象，导致井口装置与管路不同程度变形。目前正在开发的气田难度大，并且配产远高于前期高温高压气井，所以会面临更严峻的井口抬升问题与安全生产隐患，急需研究行之有效的井口抬升监控技术[1-2]。

2 “三高”气井井口抬升预测技术

目前已有的井口抬升高度预测模型，大多主要考虑温度效应，或在温度场和压力场单独作用下的影响，预测结果与现场实测数据存在10%～50%的误差，不能充分反映井口抬升真实高度。为此，本文结合海上平台实际情况，建立考虑温度效应、环空带压、套管-水泥环-地层组合体胶结效果的井口抬升高度预测模型。同时，建议以下五种情况及其他必要需求时应进行井口抬升计算：井口最高温度与环境温度差值超过60 ℃、生产套管自由段长度超过1 000 m、储层温度超过150 ℃油井、储层温度超过120 ℃气井、计划使用栽丝连接式井口。

2.1 热应力计算

套管和水泥环的热应力是井口抬升最主要的诱因。气井生产过程中，产量的变化会致井筒温度场分布发生改变，进而产生套管和水泥环的热应力。建立套管和水泥环的热应力计算模型时，假设套管、水泥环条件如下：(1)材料呈线弹性、各向同性，均在小变形范围内，不考虑屈曲对套管的影响；(2)膨胀系数为常数，不考虑材料膨胀系数随温度的变化；(3)变形均在允许范围内，忽略温度对套管材料屈服强度的影响。以井口为坐标原点，Z轴沿井眼轨迹方向取向下为正，不考虑套管-水泥环胶结力时温度变化引起的各层套管与水泥环轴向载荷，Fz应等于其轴向位移Δl与轴向刚度K之积：

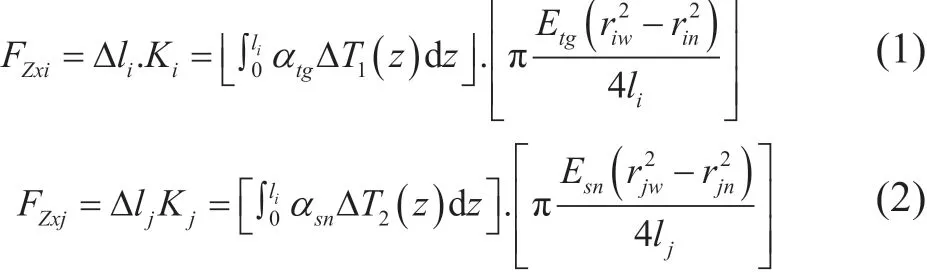
式中：Δli为第i层套管在温度场下的轴向变形(m)；Δlj为第j层水泥环在温度场下的轴向变形(m)；li为第i层套管的长度(m)；lj为第j层水泥环的长度(m)；αtg为套管的线热膨胀系数(℃-1)；αsn为水泥环的线热膨胀系数(℃-1)；ΔT1(z)为投产后套管在z处的温度变化(℃)；ΔT2(z)为投产后水泥环在z处的温度变化(℃)；Ki为第i层套管的轴向刚度(kN)；Kj为第j层水泥环的轴向刚度(kN)；Etg为套管的杨氏模量(kN2)；Esn为水泥环的杨氏模量(kN2)；Fzxi为第i层套管的轴向载荷(N)；Fzxj为第j层水泥环的轴向载荷(N)。

井筒温度场作用下不考虑套管-水泥环胶结力时各层套管和水泥环的径向体积变化量为：

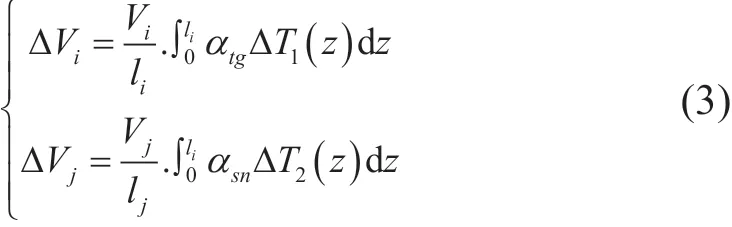
式中：Vi为第i层套管的原始体积(m3)；Vj为第j层水泥环的原始体积(m3)；∆Vi为第i层套管的热膨胀体积(m3)；∆Vj为第j层水泥环的热膨胀体积(m3)。

假设套管和水泥环不发生轴向变形，体积的变化都发生在径向，则膨胀导致的径向载荷为：

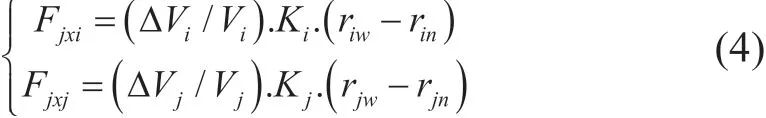
式中：Fjxi为第i层套管的径向载荷(N)；Fjxj为第j层水泥环的径向载荷(N)。

2.2 环空带压计算

在油气井的生产过程中，温度或其他复杂效应的共同作用会在环空顶部产生持续作用于套管头的高压，造成井口装置受压抬升；同时也会与液柱压力一起形成梯度压力，作用于套管壁，产生径向压力。建立环空带压造成的井口抬升计算模型时，假设以下条件：(1)不考虑各环空泄漏、串流等情况，假设所有环空在密闭环境中；(2)不考虑环空流体的密度变化；(3)不考虑环空流体与水泥环、套管之间的化学反应。环空带压造成的井口抬升力为轴向环空压力Fhi，即：

式中：Phk为轴向带压(MPa)。环空带压与液柱压力一起形成的梯度压力为径向环空压力，即：

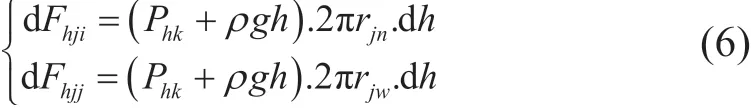
式中：Fhji为套管内壁所受的径向环空压力(N)；Fhjj为套管外壁所受的径向环空压力(N)；ρ为环空流体密度(g/cm3)。

环空带压造成的井口抬升高度为：

式中：M为井口装置的重量(N)。

2.3 界面胶结力计算

固井后，套管与地层之间、套管与套管之间的水泥环将套管和地层粘结，两个界面处的胶结力会阻碍井口抬升。胶结力的大小与热应力和环空压力以及地层均相关。建立胶结力计算模型时，假设套管、水泥环条件如下：(1)材料呈线弹性、各向同性，均在小变形范围内；(2)变形均在允许范围内，忽略温度对套管材料屈服强度的影响；(3)胶结面胶结质量一样，不考虑环空流体与水泥环、套管之间的化学反应；(4)不考虑各环空泄漏、串流等情况，假设所有环空在密闭环境中。地层会对井筒产生轴向载荷，影响井口抬升力，也会产生径向载荷，影响交界面的胶结力。根据弹性力学理论，地层对井筒的径向应力为：

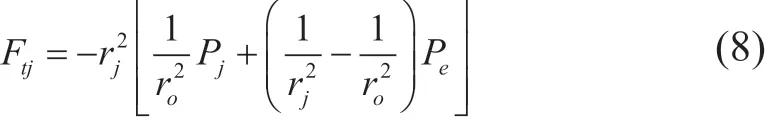
式中：Pe为径向原始地应力(N)；Pj为井筒与地层接触界面的压力(N)；rj为井眼半径(m)；ro为油管内径(m)。水泥环和地层之间的黏结力依据混凝土重力坝与基岩交界面的断裂力学方法进行计算。水泥环和地层之间的黏结强力Fjj与地应力、环空压力和热应力有关，可以表示为：

式中：Fjj为水泥环与地层之间的抗剪断的黏结强度(MPa)；Ajj为胶结面的面积(m2)；ΣQ为作用在胶结面上的全部的切向作用力(N)；ΣP为作用在胶结面上的全部的法向作用力(N)；K′为考虑抗剪断强度时的抗滑稳定安全系数，其值一般取3.0、2.50；f′为胶结面的抗剪断系数，其值一般取1.0～1.5。

作用在胶结面上的全部的切向作用力ΣQ为：

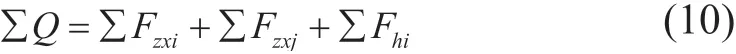
作用在胶结面上的全部的法向作用力ΣP为：

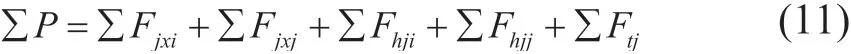
另外，也需考虑套管和水泥环之间的胶结力大小，主要由侧向应力、水泥环收缩作用和套管柱拉伸泊松效应共同产生。套管与水泥环界面复杂侧向应力：

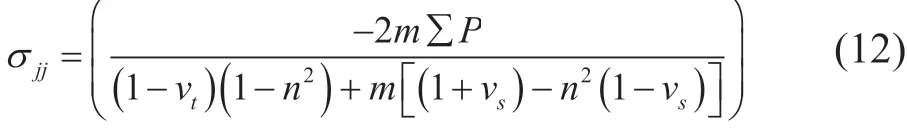
式中：m=Etg/Esn，n=rt/rs；rs、rt分别为水泥环、套管的外径(m)；νs、νt分别为水泥环、套管的泊松比。假定外围混凝土产生各向均匀收缩，其收缩应变为ε0，并在套管与水泥环界面上产生挤压正应力σss，可求得混凝土收缩引起的套管与水泥环界面上的正应力为：

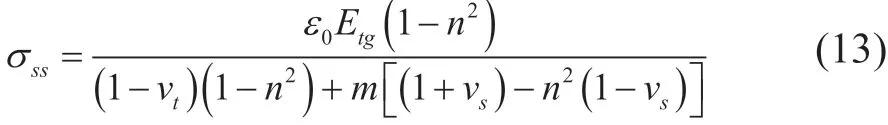
套管拉伸泊松效应引起的套管与水泥环界面上的正应力为：

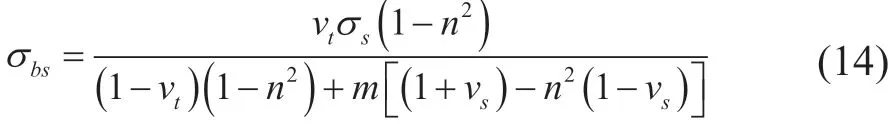
假设钢筋表面与混凝土之间的摩擦系数为µ，则对该钢筋单元可建立平衡方程：

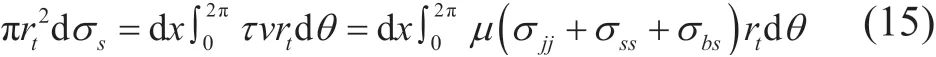
式中：D为常数系数；lb为相对锚固长度(m)。

由于每层套管都是固定在套管头上，所以水泥环与管柱之间的胶结力都会作用套管头，管柱与水泥环之间的胶结力为：

2.4 井口抬升判断及高度计算

考虑自由套管段的轴向变形与轴向热应力，假定不存在屈曲作用，则自由套管段的轴向热应力为：

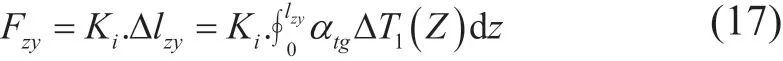
是否产生井口抬升取决于地层、水泥环和套管之间的胶结是否遭到破坏。即若Fts>Fjj或者Fts>Fcj则会发生井口抬升。总井口抬升力为：

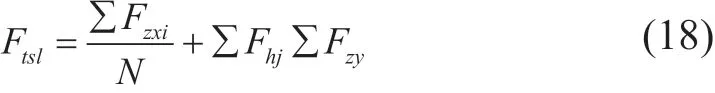
如某个胶结面出现了胶结破坏，则该界面处将不存在胶结力，井口抬升则需要克服胶结破坏面的摩擦力，而摩擦力与交界面所受垂向应力直接相关，则胶结面破坏后所要克服的摩擦力为：

最终井口抬升高度为：

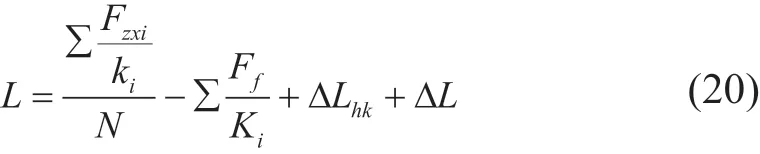
3 现场应用

利用上述前文建立的井口抬升模型对在生产的几口高温高压井进行理论计算，并与现场的实测生产数据对比，以验证理论模型的可靠性。从现场提供的每口井的实测数据中，选取5个同时有温度、A环空压力和井口抬升数据的有效时间点，表1是5口井的理论计算结果与实测值的对比。

表1 计算结果

由表1可以看出：所建立的井口抬升预测模型的理论计算值与实际监测值的误差不超过10%，保持较好的一致性。由于模型考虑了较多热力学参数，对热力学的求解结果影响较大，并且井下实际水泥环胶结质量无法确定，因此井口抬升分布结果存在一定差异。

4 结语

(1)通过对井口抬升原理的研究分析，综合考虑温度效应、环空带压与套管-水泥环-地层组合体胶结质量三个主要因素的共同影响，建立气井生产阶段的井口抬升预测模型。采用该模型演算预测了南海某高温高压气田井口装置抬升高度，计算结果与现场实际数据基本吻合，误差不超过10%，满足现场运用所需精度要求。计算结果表明井口抬升在三高气井中随产量增加会有明显上升，三高气井更严重的环空带压也会加剧井口抬升现象。(2)对于容易发生井口抬升的三高气井，在其温度压力场平衡之前，应当控制其产量位于安全阈值之下，尤其避免较大的产量波动，同时控制缓解环空带压现象。