三角形棒束内铅铋湍流普朗特数模型研究

刘书勇 余大利 梅华平 汪 振 张世超 李桃生

1（中国科学院合肥物质科学研究院核能安全技术研究所 合肥 230031）

2（中国科学技术大学 合肥 230026）

3（清华大学先进反应堆工程与安全教育部重点实验室 北京 100084）

铅冷快堆采用液态铅或液态铅铋作为冷却剂，被第四代核能系统国际论坛选为6 种候选堆型之一［1］。准确预测燃料组件棒束通道内的传热特性和热点温度对于燃料芯块与包壳的安全运行限值设计至关重要。常规介质（如空气或水）的普朗特数约为1，计算流体动力学（Computational Fluid Dynamics，CFD）商业软件代码中默认的雷诺比拟可以获得准确结果，而液态铅铋的普朗特数极小，为10−2量级，温度边界层相比速度边界层厚很多，雷诺比拟则不再适用［2］。

常用湍流普朗特数的解析解表征液态铅铋湍流模式下近壁面温度边界层与速度边界层的关系。对于湍流普朗特数模型的研究最初是基于圆管结构，Kays［3］和Jischa［4］等学者推导出圆管内湍流普朗特数关系式。Vodret 等［5］采用雷诺平均数值模拟方法研究圆管内低普朗特数流体的湍流传热特性，发现Kays 模型的计算结果与直接数值模拟以及大涡模拟结果较为吻合。陈飞［6］采用数值模拟方法对圆管内液态铅铋4种湍流普朗特数模型的适用性进行分析，恒热流条件下Cheng 模型分析结果与换热关联式吻合较好。王琛［7］开展了圆管内液态铅铋合金的传热特性实验与CFD数值模拟，探讨了不同湍流普朗特数模型对计算结果的影响，研究表明湍流普朗特数模型采用Cheng-Tak 模型时模拟与实验偏差较小。

对于棒束子通道结构的研究相对较少，Cheng等［8］结合节径比为1.75的液态汞冷却三角形棒束实验数据拟合得到棒束子通道内液态铅铋的湍流普朗特数关系式，适用于节径比P/D≥1.3的方形与三角形棒束结构。葛志浩等［9］分析节径比为1.2与1.4两种分析模型的棒束子通道内液态铅铋湍流换热，对比Graber 学者提出的换热关联式结果，发现采用Kays 和Aoki 两位学者提出的湍流普朗特数模型以及恒定湍流普朗特数为1.5 都是可以接受的。但针对三角形棒束子通道结构的研究均没有考虑节径比对湍流普朗特数的影响，作为对比的液态汞冷却实验数据仅考虑节径比为1.75 工况，并且Graber 学者提出的换热关联式与液态铅铋环境的适用性也有待实验验证。

因此本文归纳整理液态铅铋实验验证的三角形棒束换热关联式，对棒束子通道内各湍流普朗特数模型的适用性进行了分析，研究不同棒径与节径比对湍流普朗特数的影响。本研究结论可为不同节径比条件下三角形棒束子通道内铅铋传热特性的预测提供参考。

1 湍流普朗特数模型的选取

与分子普朗特数类似，湍流普朗特数Prt定义为动量涡流扩散率εM与传热涡流扩散率εH的比值。由于液态金属的分子普朗特数很小，雷诺比拟不再适用，Aoki［10］、Reynolds［11］和Jischa［4］等学者分别提出适用于液态金属的整体Prt，他们都认为与雷诺数Re和分子普朗特数Pr有关，其表达式为：

Cheng 等［8］结合1964 年Maresca 与Dwyer 学者开展的液态汞冷却三角形棒束实验（棒径为12.7 mm、节径比为1.75、加热段长度1.37 m），通过CFX程序验证提出节径比P/D≥1.3方形子通道与三角形子通道中液态金属的湍流普朗特数模型：

式中：Pe为贝克莱数。

Kays［3］提出渐进曲线形式的湍流普朗特数解析解：

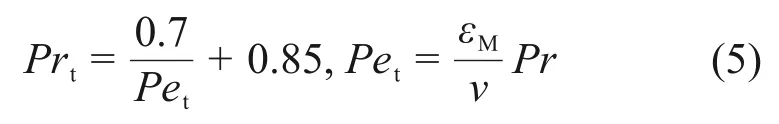
式中：Pet为湍流贝克莱数；εM为动量涡流扩散率；v为流体运动黏度系数。该关系式与Reynolds提出的方程形式（2）类似，但是Kays定义中Prt表示局部特征，Reynolds的定义中Prt是整个边界层的平均值。

作为对比，本文也列出CFD商业软件代码中默认经典雷诺比拟的Prt模型关系式：

2 数值分析模型及验证

液态铅铋环境下棒径为D、棒间距为P的三角形棒束子通道如图1 所示，由于子通道内流体流动与传热的对称性，以1/6子通道模型（图中阴影区域）作为计算区域［5，8‒9］。5 种不同分析模型参数如表1所示，分别包含7组分析算例，对比研究不同棒径与节径比下湍流普朗特数模型分析液态铅铋传热特性的准确性，计算流速满足铅铋腐蚀限值要求。子通道长度与水力直径的比值均超过67，则认为子通道出口截面流体充分发展［8］。

图1 分析模型示意图Fig.1 Diagram of analysis model

模拟采用Ansys Fluent流体力学分析程序［12］，模型采用三维结构化网格，模型边界条件设置如图2所示，加热棒壁面为恒定热流密度与无滑移壁面，进口采用573 K 恒定温度与均匀流速进口边界条件，出口为自由流出口，冷却剂由进口流入、出口流出，其中流速及对应的热流密度参数设置见表1。

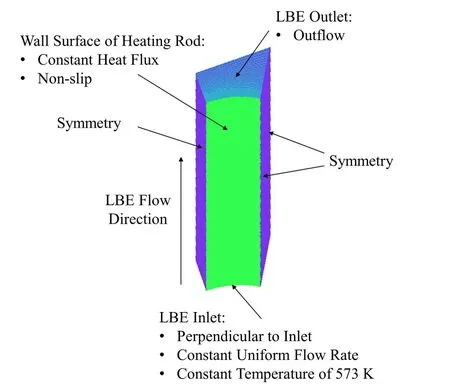
图2 计算模型的边界条件Fig.2 Boundary condition for the calculation model

图3为D12_PD1.5分析模型的网格无关性分析结果，模型中选取冷却剂进口流速0.9 m·s−1，对应加热棒壁面热流密度272 kW·m−2，选取4 万、14 万、30万、115 万、312 万和784 万网格量进行分析，网格量超过14 万后子通道出口位置的加热棒壁面温度分布变化不大，本文选取网格量115万。其余4组分析模型经过网格无关性分析确定的网格量如表1所示。

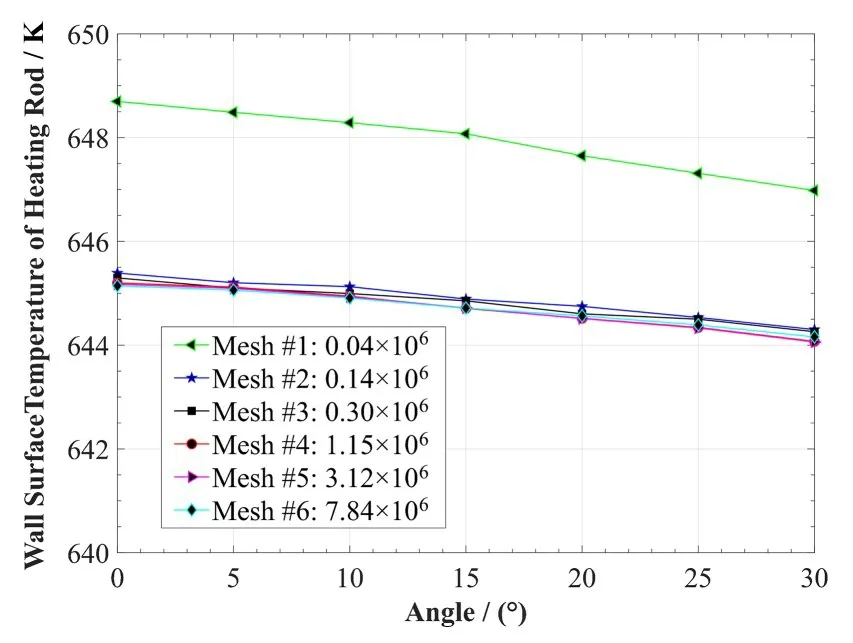
图3 网格无关性分析Fig.3 Analysis of grid independence

表1 分析模型参数Table 1 Parameters used for analysis model

选取SSTk-ω湍流模型，该模型虽不能捕捉液态铅铋子通道间的二次流特性，但是可以精确预测低普朗特数流体的整体传热特性［8，13］。对于压力-速度耦合计算是采用压力耦合方程组的半隐式方法（Semi-Implicit Method for Pressure Linked Equations，SIMPLE）算法，梯度采用最小二乘法，压力采用标准单元法，对于动量、湍动能、耗散率、能量等方程中其他每一个量均采用二阶迎风单元法进行空间离散［5］。模拟采用的液态铅铋物性包括密度、定压热容、热导率和动力黏度等都随温度的变化而变化，参照液态铅铋手册推荐的热物性关系式［2］。

为了验证分析程序的准确性，如表2所示，本文对Vodret 学者开展的先进铅冷快堆欧洲示范堆ALFRED堆芯组件传热计算结果进行了比较［5］。湍流普朗特数模型采用Kays 提出的关系式（5），本文程序预测努塞尔数Nu值与Ushakov 推荐关联式具有较好的一致性，与Mikityuk 推荐关联式对比绝对误差优于增强壁面函数法计算结果，验证了本分析程序的准确性。

表2 程序验证的子通道参数设置及结果对比Table 2 Sub-channel parameters for program verification and comparison of results

基于三角形棒束子通道内汞和钠钾合金等液态金属的实验数据，Mikityuk、Ushakov、Borishanskii和Kazimi 等学者分别提出液态金属的努塞尔数Nu换热关联式，如表3所示。

表3 液态金属换热关联式Table 3 Heat transfer correlation equations for liquid metal

由于液态铅铋具有高密度、低热导率和较强的自然循环特性，使得其与钠钾合金等碱金属的湍流传热与浮升力特性具有很大的不同，液态铅铋的传热性能也低于液态碱金属［18］。基于液态汞和钠钾合金获得的液态金属努塞尔数Nu换热关联式需通过液态铅铋实验验证。

为探究三角形棒束子通道内液态铅铋的流动传热特性，德国KIT 和意大利ENEA 等多家单位搭建液态铅铋组件实验装置开展研究，获得的实验结果对换热关联式进行了验证，组件结构参数与验证的关联式如表4 所示。Mikityuk 提出关联式（7）具有更广泛的适用性，与三个实验装置的测试结果吻合，在节径比1.282~1.8范围内验证准确，因此本文以该关系式作为对比，在表1 分析模型中节径比P/D与贝克莱数Pe均在Mikityuk 提出的Nu换热关联式（7）适用范围内。

表4 液态铅铋换热关联式实验验证Table 4 Experimental verification of heat transfer correlation equations for liquid lead-bismuth

3 计算结果与换热关联式的对比

努塞尔数Nu是反映对流传热特性的无量纲量，基于当地努塞尔数NuL定义，其公式表达为［24］：

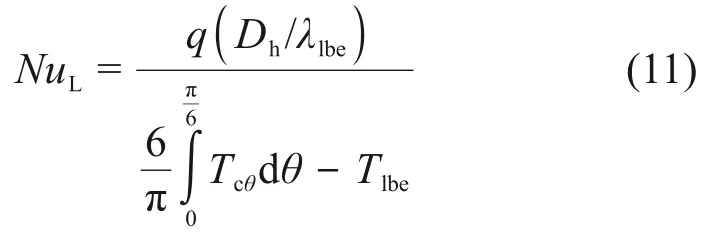
式中：q为热流密度；λlbe为冷却剂热导率；θ为角度；Tcθ为当地包壳温度；Tlbe为冷却剂平均温度，后文分析的努塞尔数Nu均指分析子通道出口截面位置的当地努塞尔数NuL。

对于表1 节径比为1.3 的3 种分析模型，在不同贝克莱数Pe下分别采用§1 中5 种湍流普朗特数模型，对努塞尔数Nu进行预测，其结果如图4 所示。为了便于对比，图4 中也给出了Mikityuk 关系式计算值、恒定湍流普朗特数Prt=1.5的预测值以及采用雷诺比拟（Prt=0.85）的预测值等曲线。

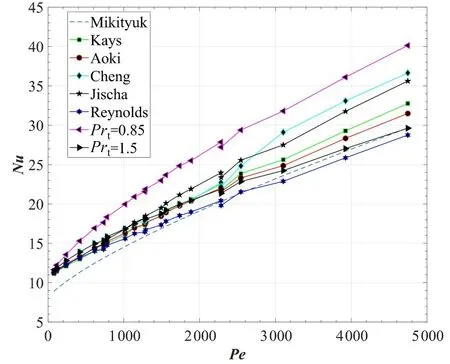
图4 不同湍流普朗特数模型预测结果与Mikityuk换热关联式对比（P/D=1.3）Fig.4 Comparison of prediction results of various Prt models with that of Mikityuk heat transfer correlation(P/D=1.3)

由图4 可见，各种Prt模型预测值的总体趋势与Mikityuk关系式计算值是一致的，随贝克莱数Pe增加而线性增加。经典雷诺比拟不适用于低普朗特数流体，在78≤Pe≤4 700 范围内均高于其他Prt模型预测值，与Mikityuk 关系式计算值最大偏差为35%。当恒定Prt=1.5 时，仅在Pe高于3 000 时与Mikityuk关系式计算曲线较为吻合，最大偏差为2.6%。而在整个Pe范围内，除Reynolds模型外其他模型均高估低普朗特数流体的传热性能。当采用Reynolds模型时与Mikityuk关系式计算曲线较为吻合，在高Pe数时发展斜率也基本一致。在Pe≈2 300时，各种Prt模型预测值均出现小幅度下降，这是由于棒径12 mm与棒径25 mm两种不同棒径的分析模型预测值稍有偏差，但影响相对较小。

节径比为1.5 和1.7 的Prt模型预测结果与Mikityuk 换热关联式分别如图5、6 所示。雷诺比拟预测传热性能同样高于其他Prt模型，与Mikityuk关系式计算值最大偏差为15.8%。当贝克莱数Pe高于1 000 时，Kays、Aoki 和Reynolds 模型与恒定Prt=1.5模型均低估低普朗特数流体的传热性能。湍流普朗特数采用Cheng 模型时只有当Pe高于2 000 时与Mikityuk 关系式计算曲线吻合较好，最大偏差7%。当节径比为1.5和1.7时，Jischa湍流普朗特数模型在整个贝克莱数Pe范围内均能很好地预测低普朗特数流体的传热性能，表明Jischa 模型预测的湍流普朗特数值与Prt理论计算值较为吻合。

图5 不同湍流普朗特数模型预测结果与Mikityuk换热关联式对比（P/D=1.5）Fig.5 Comparison of prediction results of various Prt models with that of Mikityuk heat transfer correlation(P/D=1.5)

为了对比不同Prt模型在整个节径比（1.282~1.8）范围内的适用性，通过整理上述Prt模型预测Nu值，并与Mikityuk 关系式计算Nu值进行比较，以求得平均绝对误差εˉ、标准差σ与均方根误差γ，表达式分别为：

式中：εi为Mikityuk关系式计算Nu值与Prt模型预测Nu值的偏差；N为算例数；平均绝对误差εˉ反映Prt模型预测Nu值误差的平均值；标准差σ反映N组Prt模型预测Nu值偏差εi与平均值的离散程度，σ越小，说明预测值偏差越接近平均值；而均方根误差γ用来评价N组Prt模型预测Nu值与Mikityuk 关系式计算Nu值的变化程度，γ越小，说明预测模型描述真实数据具有更好的精确度。

这三种误差的计算结果如表5 所示，经典雷诺比拟预测Nu值误差较大；在节径比为1.3 时，Reynolds 模型可以得到很好的预测结果（均方根误差均低于1.38）；Cheng 模型在节径比为1.7 时，计算结果与Mikityuk 关系式计算值误差较小（均方根误差均低于0.96）；而在节径比为1.5~1.7 时，Jischa 模型预测结果较好（均方根误差低于0.83）。在整个节径比（1.3~1.7）范围内，采用Kays湍流普朗特数模型时，数值模拟结果与Mikityuk 关系式计算值误差较小（总体均方根误差低于2.22），在各种节径比下预测效果不是最优的，但是属于普适性较好且整体范围内预测效果较好的Prt模型；Aoki模型的整体预测效果仅次于Kays模型。

表5 不同湍流普朗特数模型预测Nu值的误差Table 5 Prediction error of Nu for different Prt models

图7 给出了Kays 模型数值模拟预测结果与Mikityuk换热关联式计算Nu数值对比结果，由此可见，在低Pe工况整体预测Nu数值偏大，而在高Pe工况整体预测Nu数值偏小。表6 为不同Pe范围内Kays模型预测Nu值的误差，低Pe工况比高Pe具有较小的平均绝对误差εˉ与均方根误差γ，表明Kays模型在低Pe工况的预测准确度较优于高Pe工况。

表6 不同Pe范围内Kays模型预测Nu值的误差Table 6 Prediction error of Nu for Kays models during different Pe conditions

图7 Kays模型预测Nu值与Mikityuk关系式计算Nu值对比Fig.7 Nu value predicted by the Kays model vs.the Nu value recommended by Mikityuk correlation

整理图4~图6 各分析模型中准确预测Nu数值的Prt，绘制了与Pe关系曲线如图8 所示。可以看出，Prt与Pe关系曲线类似于渐进曲线，在节径比一定的情况下随Pe增加趋近于恒定数值，节径比越大，趋近数值越小（节径比为1.3、1.5和1.7时分别趋近于1.5、1.08和1）。因此整体湍流普朗特数模型不仅与Re、Pe有关，还与节径比P/D有关。

图6 不同湍流普朗特数模型预测结果与Mikityuk换热关联式对比（P/D=1.7）Fig.6 Comparison of prediction results of various Prt models with that of Mikityuk heat transfer correlation(P/D=1.7)

图8 不同分析模型的Prt值对比Fig.8 Comparison of Prt values of different analysis models

4 结语

针对5 种不同的湍流普朗特数模型，在不同棒径与节径比的棒束子通道结构下开展了35 组工况的数值模拟，通过对液态铅铋实验验证的Mikityuk换热关联式计算结果比较，可得出如下结论：

1）整体湍流普朗特数模型不仅与Re、Pe有关，还与节径比P/D有关，在节径比一定的情况下随Pe增加趋近于恒定数值，节径比越大，趋近数值越小。

2）各种湍流普朗特数模型均有最佳的节径比适用范围。在节径比为1.3 时，当Prt模型采用Reynolds模型预测值较好；在节径比在1.5~1.7范围内时采用Jischa 模型与Mikityuk 关系式计算曲线较为吻合；Cheng 模型适用于节径比为1.7 工况；节径比在1.3~1.7 范围内时Kays 模型的普适性较好，Aoki模型的预测效果次之。

3）棒径对湍流普朗特数模型的影响相对较小。

由于低Pe的低普朗特数流体传热可能受浮升力影响，本文所述的Prt模型在低Pe的预测效果有待进一步研究，提升低普朗特数流体在强迫转自然循环以及自然循环建立工况下的传热性能预测精度。

作者贡献声明刘书勇：负责文章的撰写与模拟；余大利：负责文中湍流普朗特数模型的收集与整理；梅华平：负责模拟结果数据的后处理与出图；汪振：负责文章章节框架的设计；张世超：负责液态铅铋实验验证换热关联式的收集与整理；李桃生：负责研究的提出与设计。