升弓过程中弓网电弧及接触线温升特性分析
2022-03-22杨盼奎佘鹏鹏廖前华李成坤魏文赋
杨盼奎,佘鹏鹏,廖前华,李成坤,魏文赋
(1.中车青岛四方机车车辆股份有限公司,青岛 266000;2.西南交通大学电气工程学院,成都 611756)
高速列车由于运行速度高、舒适性好、准时性好等众多优点,在我国运行里程数越来越高,在我国人民生活生产的交通运输各领域扮演着愈发重要的角色。随着人民对交通运输时效性以及运输量要求的不断提高,高速列车运输速度与容量进一步提高[1-2]。然而,由于列车升降弓、机械振动、接触线覆冰等因素导致的弓网离线会产生弓网电弧[3-7]。弓网离线电弧的产生不仅会降低弓网受流质量,影响牵引供电系统,并且弓网电弧的高温会加剧受电弓滑板与接触线的烧蚀损耗[8-9]。对动态升降弓电弧特性的影响开展研究,对于深入理解弓网电弧侵蚀弓网材料机理并提出相应措施具有重要意义。
基于电极材料电弧燃弧及侵蚀问题,目前国内外学者针对高速铁路弓网系统电弧燃弧已经开展了大量实验及仿真研究。研究方式主要采用实验研究[10-13]、电路仿真[12-13]以及磁流体模型仿真[13-14]等方法。电弧磁流体仿真模型通过耦合电场、磁场、热场以及流场对电弧多物理场进行耦合分析,是当下一种运用广泛的电弧研究手段。韩伟锋等研究了静态弓网电弧弧柱以及弓网电极的温度场分布,研究表明受电弓滑板受弓网电弧热作用的侵蚀程度大于运行中不断变换区域的接触线,提高受电弓滑板的热导率可以有效减轻电弧对材料的侵蚀作用。ZHU Guangya等[14]基于弓网磁流体仿真模型,从弓网间隙距离这一重要因素对弓网电弧燃弧温度及气流场的影响进行了研究,发现弓网间隙变化对弓网材料的温升具有较大影响。GAO Guoqiang[15],韩伟峰等[16]建立了降弓过程弓网电弧分析模型,从不同电弧电流、站内降弓速度等因素对降弓电弧温度场及气流特性进行研究,发现降弓速度越大,电极运动引起的气流场变化对于电弧形态的影响也越大,电弧电流对电弧温度的影响较大。乔凯等[17]搭建改进的Mayr电弧模型,对比分析弓网离线电弧仿真波形和实验波形,发现随着列车运行速度提高和离线间距的增大,气流对电弧的吹弧作用更加显著,电弧耗散功率增加,燃弧尖峰电压和熄弧尖峰电压增大。上述研究主要针对稳态以及降弓状态下的弓网电弧进行研究分析,而对于升弓电弧并未展开相应研究。且升弓受流时列车一般处于站内静止,弓网无相对滑动。燃弧对接触线单点的持续热作用使接触线受烧蚀严重。基于上述现状,亟需开展升弓过程中弓网电弧以及接触线温度场分布的研究。本文运用COMSOL电流、磁场、传热以及层流四大模块,基于电弧MHD模型建立了升弓过程中弓网电弧模型,从升弓速度对弓网电弧以及接触线温度场特性进行了研究。
1 模型描述
列车在站内启动时首先进行升弓操作完成弓网接触,受电弓滑板在机械臂作用下上升至接触线接触受流并形成受流回流回路,为列车运行提供能量。在列车受电弓升弓时,受电弓与接触网两电极之间距离逐渐缩短,当缩短到一定距离时较高的电压会使得空气被击穿致使电弧产生,且由于柔性接触网的张力使得弓网两电极进行弹跳分离,使得电弧反复发生。由于此时列车尚未运动,受电弓与接触网导线处于相对静止状态,升弓电弧将会定点烧蚀接触线,热作用对接触线的侵蚀和损伤将影响受流回流系统进而影响列车正常运作。基于上述工况,本文基于MHD理论建立二维升弓电弧分析模型。
1.1 几何模型与物性参数
基于磁流体模型建立的升弓电弧几何模型如图1所示。模型整体框架几何参数为20 mm×25 mm,接触线下轮廓半圆半径为6.5 mm,受电弓滑板的几何参数为20 mm×5 mm。接触线采用铜电极材料,滑板材料使用粉末冶金材料的物性参数。仿真中接触线与受电弓滑板的主要物性参数有影响传热的热导率、比热容,以及导电的电导率、密度等。各具体物理参数见表1。
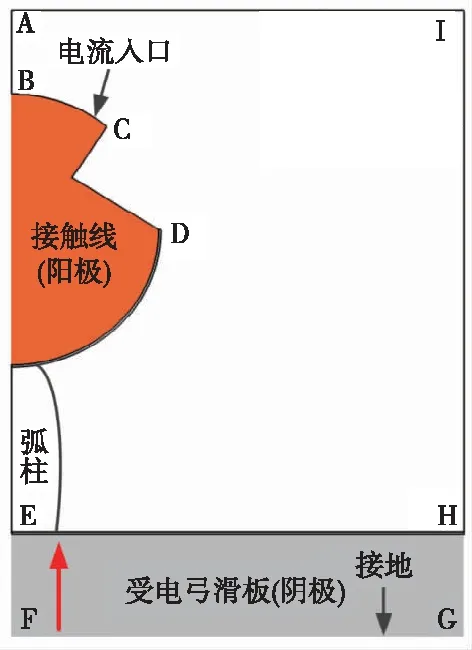
图1 仿真几何模型

表1 接触线与受电弓滑板的物理参数
1.2 电弧数学模型
目前弓网电弧燃弧及侵蚀模型主要是基于(MHD)磁流体动力学理论运用Ansys Fluent或COMSOL建立的,这其中包括传热层流磁场电场四大模块,同时分别包含流体动力学以及电磁场各类方程。其中流体动力学方程是指将质量、动量和能量三者在流体运动中的联系,包含流体质量守恒方程、动量守恒方程与能量守恒方程三部分。本文采用Maxwell方程组针对电磁场方程进行描述,其中主要以Maxwell方程组为主,以及库仑定律、静电场和恒定磁场的基本方程。基于磁流体动力学模型,认为弓网电弧区域处于局部热力学平衡(Local Temperature Equal)状态,电弧燃弧过程中高温粒子流体流动处于层流状态。软件模型内部流体动力学方程与电磁场方程[18]如下。
(1)流体动力学方程
流体动力学方程包含流体质量守恒、动量守恒方程与能量守恒方程方程三部分。具体方程形式如下。
①流体质量守恒方程
(1)
②动量守恒方程
(2)
③能量方程
(3)
(4)
在上述方程中,v为流场速度矢量;ρ为电弧密度;vi为i=(r,z)方向上的速度分量;η为动力黏度;p为压强;J为电流密度;B为磁感应强度;T为温度;H为焓;λ为热导率;cp为比热容;能量方程源项Q包括焦耳热源项J2/σ,辐射源项QRad以及黏性耗散项V。本文采用体积净辐射系数法计算热辐射,如式(5)
Qrad=4πεn
(5)
式中,εn为与温度相关的体积净辐射系数,本文采用文献[19]中计算得到的净辐射系数。
(2)电磁场方程
根据Maxwell方程组,可以求解得到电位φ
div(σgradφ)=0
(6)
电流密度为
J=-σgradφ
(7)
本文利用磁矢位计算电弧磁场
div(gradA)=-μ0J
(8)
B=∇×A
(9)
式中,A为磁矢位;μ0为真空磁导率。
1.3 边界条件
本文仿真设置的边界条件如表2所示。较为关键的边界条件如下。

表2 升弓电弧仿真边界条件
对于热边界条件,空气区域外部边界AI,HI的温度设置为T0=293.15 K;接触线边界顶部BC与受电弓滑板底部FG设置为T0=293.15 K;受电弓滑板边界GH,EF考虑为对流换热边界条件
q·n=h(T-T0)
(11)
其中h=10[W/(m2K)]为对流换热系数,T为边界温度,n为表面法向量。
对于流体流动边界条件,空气区域边界AI,HI设置为压力出口边界条件p0,加载1个标准大气压(101 325 Pa)。
对于电磁场边界条件,接触线边界BC设置为电流密度边界,受电弓滑板底部边界FG设置为接地。
对于动网格边界条件,边界EF,FG,GH和EH设置为仿真边界,方向为r轴负方向;AB和HI边界的r坐标不变,z坐标可自由变化;AI边界的z方向坐标不变,r方向坐标可自由变化;BC和CD边界的z轴与r轴方向均不变化。
2 仿真结果及分析
研究中所设仿真电弧的电流大小为100 A,研究了不同升弓速度0.25,0.5,0.75 m/s和1 m/s时的升弓电弧特性。运用COMSOL动网格技术模拟列车升弓几何模型的变化过程,主要分析了电弧温度场分布、电弧电压特性、电弧流场变化等,同时提取了升弓过程中接触线的温度变化进行分析。将仿真燃弧计算时间设置为10 ms,计算步长为0.1 ms,初始的弓网间隙设置为13.5 mm。
图2是升弓速度为1 m/s时电弧温度场分布随时间的变化情况。可得电弧燃弧弧根处最高温度约为18 000 K,电弧最高温度处于电弧阴阳极弧根处,也即接触线底部和受电弓滑板顶部区域。电弧弧柱区域温度在2.5 ms时刻约为12 000 K。升弓过程中电弧被压缩弧长变短,热耗散减少,电弧弧柱温度逐渐升高。在热作用累计下到10 ms时刻时,电弧弧柱温度升高至约为14 000 K。还发现随着升弓过程的进行,受电弓与接触网两电极逐渐靠近的过程中,电弧与电极材料的鞘层区域逐渐收缩。造成电弧收缩、温度上升的主要原因可能是电弧弧长压缩,电弧弧柱电流密度增大,燃弧产生的局部磁场增强,使得电弧受洛伦兹力的影响而呈现收缩状态。

图2 不同时刻的升弓电弧温度场分布
图3显示出10 ms时刻升弓速度对电弧弧温分布的影响。可以看出,速度主要影响电弧的长度以及温度分布的区域范围。当升弓速度由0.25 m/s逐渐增大到1 m/s过程中,电弧弧柱长度由11.5 mm减小到3.5 mm。电弧区域中高温的区域(>8 000 K)宽度由8.4 mm减小到4.6 mm。
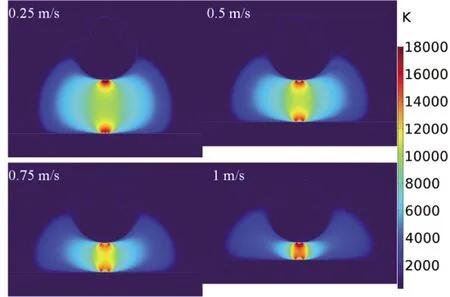
图3 不同升弓速度时电弧温度场分布
图4为升弓速度对电弧弧压的影响曲线。单一来看,可以看出随着电极距离的逐渐靠近,其电压呈现逐渐减小的趋势,且电弧弧压减小的斜率在不同的时间段呈现出不同的变化,在0~1 ms下降斜率大于1 ms之后的区域。在0~1 ms时间范围内,其一电弧弧长减小使得极间电压降低,另一方面,在此时间范围内电弧高温区域逐渐膨胀使得电弧电阻减小导致电弧电压减小。因此,综合两方面因素,电弧电压在此阶段下降更快。在1 ms之后的时间范围内,电弧弧压的减低与实践变化近似呈现线性关系。因为此阶段电弧高温区域基本稳定,电弧弧长是影响电弧电压的决定因素。纵向来看,升弓速度会显著影响电弧弧压的变化率,且是正相关的关系。升弓速度为0.25 m/s时,电弧电压由65 V变化到46.5 V。升弓速度增大到1 m/s时,电弧电压由65 V变化到29.7 V。因此电压受升弓速度影响较大。
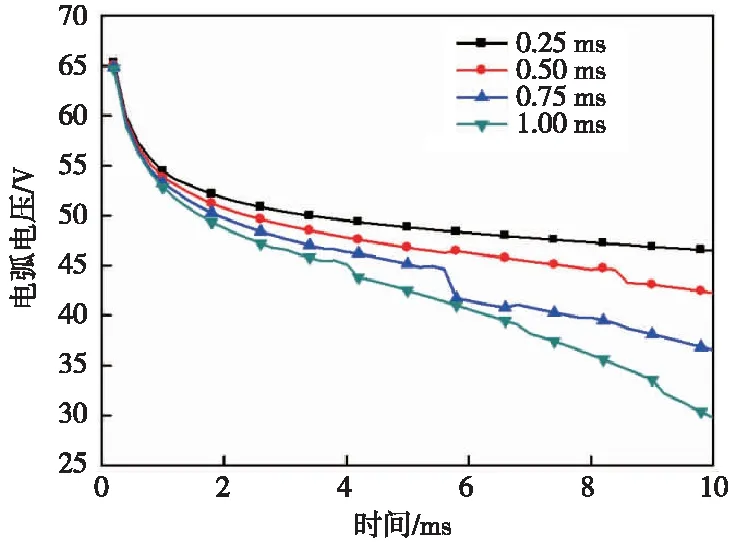
图4 不同升弓速度下电弧电压变化曲线
由于升弓时列车尚未运动处于静止状态,升弓电弧将会定点烧蚀接触线,热作用对接触线的侵蚀和损伤将影响受流回流系统进而影响列车正常运作。因此需要对升弓过程中温度场分布进行分析,当升弓速度为0.25 m/s时,10 ms时刻的接触线温度场分布如图5所示。由图5可知,接触线最高温度约为1 700 K,接触线受升弓电弧影响的高温影响区域(>300 K)约为2 mm。采用如图5所示的温度提取线提取接触线温度曲线,研究弓网燃弧时间以及升弓速度对接触线温度影响。

图5 接触线温度分布
图6为升弓速度0.25 m/s时,接触网内部不同位置处的温度与时间的变化情况。由图6可知,随着升弓电弧燃弧过程的进行,接触线内部最高温度由0.5 ms时的992 K增大到4 ms时的1351 K。接触线高温影响区域(>800 K)由0.5 ms时的0.1 mm增大到4 ms时的0.5 mm。
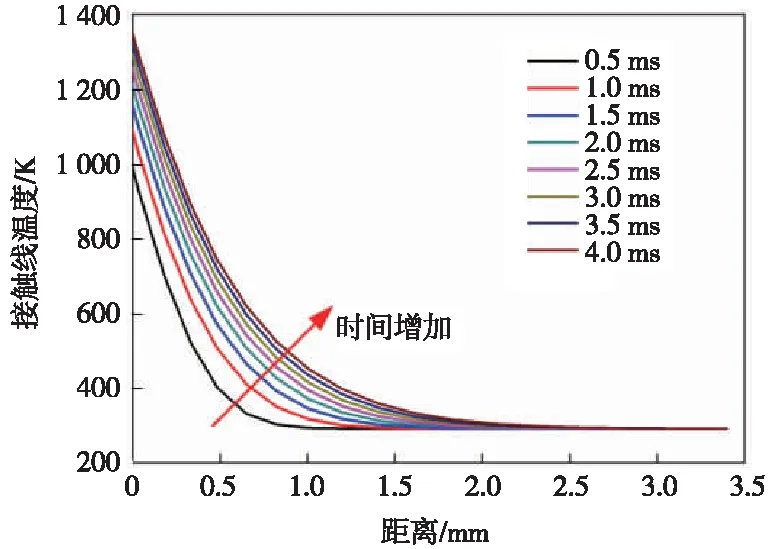
图6 接触线温度随时间的变化曲线
图7显示了接触网导线与速度的变化情况。可以看出升弓速度对于接触线最高温度具有一定的影响,而对于接触线高温区域的分布范围几乎没有影响。升弓速度由0.25 m/s增大到1 m/s时,接触线最高温度由1 351 K减小到1 161 K。
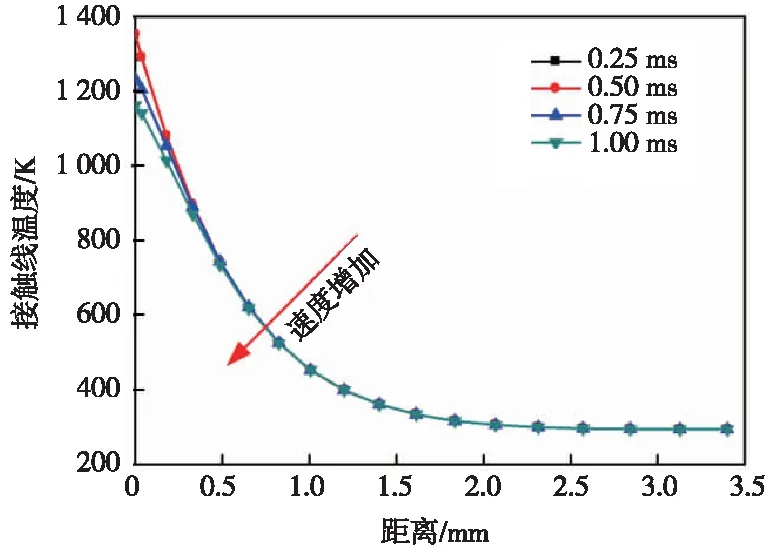
图7 接触线温度随升弓速度的变化曲线
由上面分析可知,相较于升弓速度而言,燃弧时间对接触网温度分布的影响更大,然而从另一方面分析,在整个升弓过程中,若整体间隙相同,速度越大则燃弧的时间会更短,然而考虑在间隙相同时,升弓速度更大时升弓电弧的燃弧时间更短。因此根据以上的仿真研究结果结合多方面的因素,加快升弓速度可以有效减少燃弧时间,减轻电弧燃弧热作用及电子发射[20]对接触线材料的热侵蚀作用。
3 实验验证
本研究采用课题组自制弓网升降弓实验平台,进行系列不同条件下升弓燃弧实验,并记录燃弧电压及燃弧图像,最后与仿真结果进行对比来验证仿真模型正确性。图8是升降弓实验平台装置原理图以及测试设备,升降装置为伺服电机控制精密位移台来完成升弓过程。监测设备其中包括高速相机配微距镜头记录电弧形貌,而电弧燃弧波形通过示波器测量。
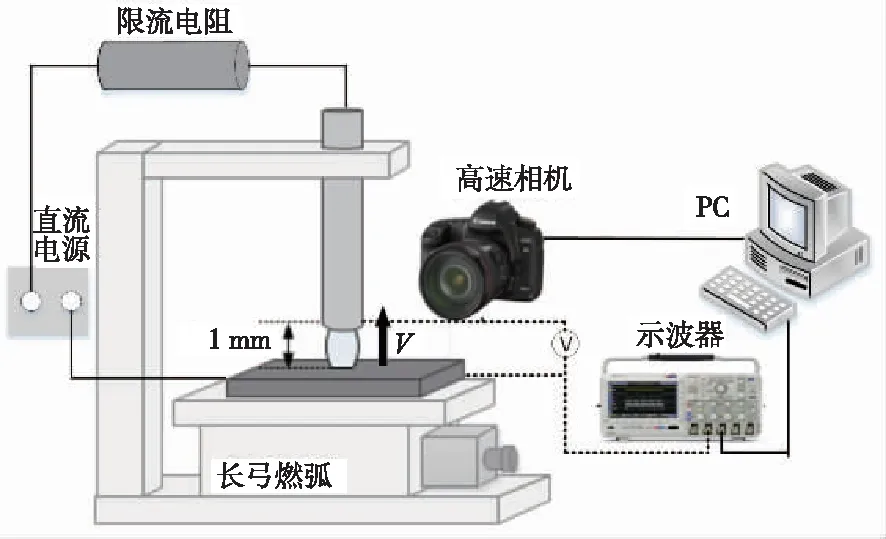
图8 实验升弓装置及原理图
本文进行了不同升弓速度下的燃弧类比实验,为了模拟仿真升弓过程,实验条件设定为 40 V,20 A。升弓速度为2、4、6、8 cm/s,并通过高速相机记录电弧形貌以及示波器记录电压电流波形。
图9显示了升弓过程中不同时刻电弧形貌,在上电极的下端和下电极的上端均出现了熔融铜材料,从此可看出,最高温度也是处于电弧直接作用的接触线底部和受电弓滑板顶部区域,也即对应的阳极弧根与阴极弧根处。随着升弓过程进行,电弧的弧长逐渐缩短,导致热量更加的集中,由此可以看出电极材料弧根区域亮度在不断的增强,在电弧弧根与电极材料接触区域面积收缩严重,弧柱整体发生了收缩现象,加剧了滑板的侵蚀。可以看出,实验与仿真具有一致性,验证了仿真的正确性。

图9 升弓过程燃弧形貌分析
紧接着也进行了不同速度下的升弓实验,将升弓速度分别设置为2、4、6、8 cm/s。升弓过程电弧弧压变化如图10所示。随着升弓过程进行,电弧电压在逐渐减小,而且前期的下降斜率大于中后期的下降斜率,这和仿真结果一致。电弧长度与电压有一定的相关性,升弓速度越快使得电极间隙变化越快,导致电压的变化速率越大,而且随着升弓继续进行,电压数值差距逐渐增大。因此升弓速度越大,电极间的距离变化更快,电压变化越快,升弓电弧越容易熄灭。实验结论一定程度上验证了前文仿真结果的正确性。
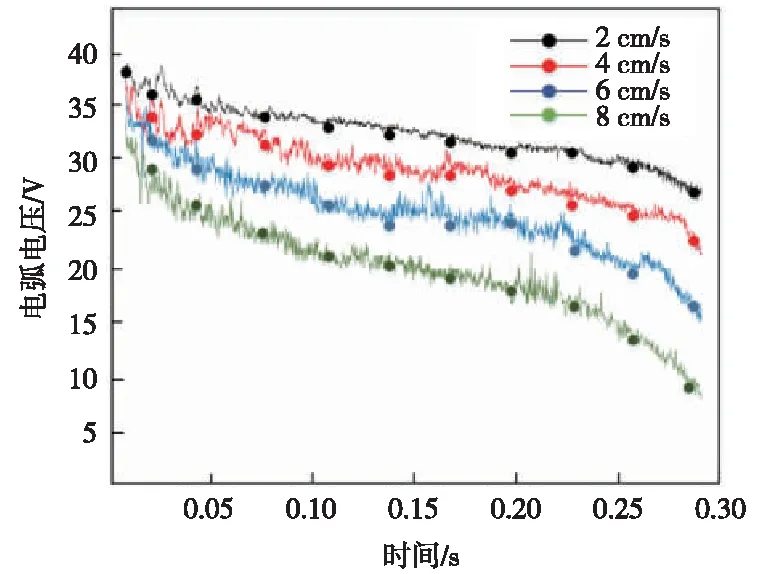
图10 升弓过程中电弧电压波形
4 结论
本文通过COMSOL多物理场仿真软件电场、磁场、传热以及层流四大模块,基于弓网电弧MHD模型以及动网格(ALE)技术,建立了二维轴对称升弓电弧以及接触线温升模型,通过动网格技术模拟升弓过程,研究了不同升弓速度对升弓电弧燃弧特性以及接触线温度场的影响。得出以下结论。
(1)随着升弓过程的进行,电弧与电极材料接触的鞘层区域逐渐收缩。造成电弧收缩、温度上升的主要原因是电弧弧长压缩,热量聚集,弧柱电流密度增大,燃弧电流产生的磁场增强,使得电弧受洛伦兹力的影响而呈现收缩状态。
(2)在升弓过程前期,由于升弓电弧弧长变短以及电弧电阻减小的影响,升弓电弧电压变化斜率更大。在升弓过程的中后期,由于受电弧弧长单方面因素的影响,电弧电压呈现近似线性减小。
(3)随着燃弧持续时间增加,接触线最高温度逐渐增大,同时高温区域的面积也逐渐增大。增大升弓速度时,接触线最高温度逐渐减小,但接触线高温区域分布范围几乎没有影响。
(4)相较于升弓速度而言,燃弧时间对接触网温度分布的影响更大,然而在整个升弓过程中,若整体间隙相同,速度越大则燃弧的时间会更短。综合考虑两方面的因素,加快升弓速度可以减少燃弧时间,进而减轻电弧对接触线的热侵蚀。
