CRTSⅢ型无砟轨道板内温度场演化特征研究

2022-03-22曾润忠胡文韬

铁道标准设计 2022年3期

曾润忠，张佳，胡文韬，金晨

(1.华东交通大学江西省岩土工程基础设施安全与控制重点实验室，南昌 330013；2.江西省地质局902大队，南昌 338000)

CRTSⅢ型无砟轨道板是我国自主研发、具有完全知识产权的一种新型高速铁路轨道结构，相较于CRTSⅠ、CRTSⅡ型轨道板，具有高平顺、高稳定、易维修等优点，被广泛用于高速铁路建设中。但由于长期暴露于自然环境中，CRTSⅢ型无砟轨道板在服役期间易受季节性温度变化及昼夜温差等外部环境的影响，在轨道板内产生随时间与外部环境变化而循环升降的温度场，造成轨道板外表面与内部的温度差异，这种内外温差作用会引起其内部的温度场发生显著变化，进而产生温度应力，当温度应力达到混凝土设计强度时，会使得轨道板发生翘曲或开裂，导致无砟轨道板力学性能和耐久性能衰退[1-2]。因此，准确地分析无砟轨道板结构的温度场分布及演化特征，可为CRTS Ⅲ无砟轨道板结构优化设计、合理施工及运营维护提供依据。同时，我国“十四五”铁路发展规划提出完善现有铁路线路网络，扩大中西部路网覆盖，优化东部网络布局，形成城际快捷交通通道，加大地区间的经济文化交流，全面助力脱贫攻坚。因此，探究CRTS Ⅲ型无砟轨道板的温度变形机理，既是高速铁路发展的需要，又能响应国家建设的号召，有着十分重要的现实意义和工程研究价值。

目前，在工程设计中广泛认为环境引起的混凝土轨道板最大正、负温度梯度取值分别为90 ℃/m、-45 ℃/m[3]，但在实际设计过程中，会基于安全性考虑而适当调整增加轨道板温度梯度设计值。戴公连等[4]基于GPD模型并对某地区轨道板实测数据进行分析，预测轨道板百年一遇的正负温度梯度计算值分别为116.8 ℃/m和-63 ℃/m；邓非凡[5]对轨道结构纵断面上不同深度处的温度进行测量，提出轨道板垂向最大正温度梯度的分布预估模型；赵坪锐等[6]利用概率统计方法对双块式无砟轨道板进行连续测试，提出了轨道板温度梯度范围及保证率；李佳雨[7]通过贝叶斯网络模型，研究并预估华东地区某线路在夏季高温环境作用的轨道板温度梯度预警值；陈帅[8]，冀磊[9]研究了刷涂反射隔热涂料对轨道板内部应力的影响；欧祖敏[10]利用气象数据资料描述边界条件，推导出轨道结构的温度场计算公式，并分析了太阳辐射、风速和气温变化等环境因素对轨道结构内部温度分布状况的影响；刘付山等[11]采用气象学基本理论，对连续式无砟轨道结构温度场进行了三维有限元模型分析。上述学者的研究成果极大地推动了人们对轨道板温度变形机理的认识，但我国高速铁路运营覆盖范围广，地域性因素影响非常突出，因此，需结合各地的实际情况对轨道板温度效应进行进一步研究。

基于此，选取昌吉赣高铁丰城段CRTSⅢ型无砟轨道结构板进行现场温度实测，通过现场实测数据与模型仿真结果对比，对温度场预估公式的合理性和准确性进行讨论，最终得到轨道板温度场的演化趋势和温度梯度分布曲线。

1 无砟轨道板温度场热量传递

1.1 一维传导方程

对无砟轨道板温度场分布进行分析时，由于轨道板侧面与空气的接触面积远小于板上表面与空气的接触面积，因此，侧面热对流引起轨道结构温度场的改变可忽略不计，可将其假定为平板状结构。假设轨道板内任一点温度只与所在的深度有关，而与该点的水平位置无关，无砟轨道板的热传递便可简化为一维热传导问题，从而满足一维不稳定导热微分方程[12]，即

(1)

式中，α(z)为轨道结构材料的导温系数，取α(z)=0.003 m2/h。

1.2 一维热传导方程验证

为验证一维热传导假定的准确性，选取昌吉赣高速铁路丰城段CRTS Ⅲ型无砟轨道结构板进行现场温度实测。轨道板为P5600型标准板，长5.6 m、宽2.5 m、厚0.2 m，养护完成后安装于丰城市三江镇大坪0号路基，第6块板，东经115°6′，北纬28°2′。该地区为亚热带湿润季风气候，整个轨道板朝向为南北走向。借鉴文献[13]中CRTSⅡ型无砟轨道板现场监测温度的实践经验，温度测点布置如图1所示，1～25号(位于板表面)为红外线枪测点，在1～3号、11～13号各测点正下方距离轨道板表面4，20 cm处埋入PT100铂电阻温度传感器，在13号点正下方距离轨道板表面8，12，16 cm处增设3处传感器测点，数据采集选用DH5922N动态信号测试分析系统，误差为0.15±0.002|t|，采样间隔为0.5 h，环境温度使用温度计测量。

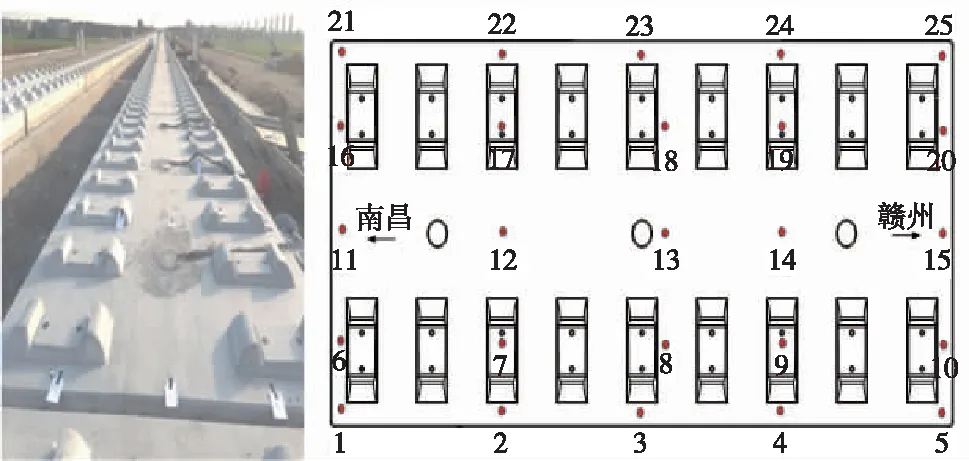
图1 轨道板温度测点布置

高温气候选取具有代表性的9月28～29日两天(环境气温为22.8～37.6 ℃)的实验数据进行分析，板面、板底在10时和14时的等温实测分布线如图2、图3所示。由图2、图3可见，轨道板上表面温度受太阳辐射影响显著，而轨道板底部呈现中间高两边低的趋势，沿轨道板长边方向近似对称。横向温差在1.4 ℃以内，相对于轨道板短边方向的温度梯度可忽略不计，由此可见，轨道板采用一维热传导假定符合工程实际情况。

图2 轨道板上表面等温线

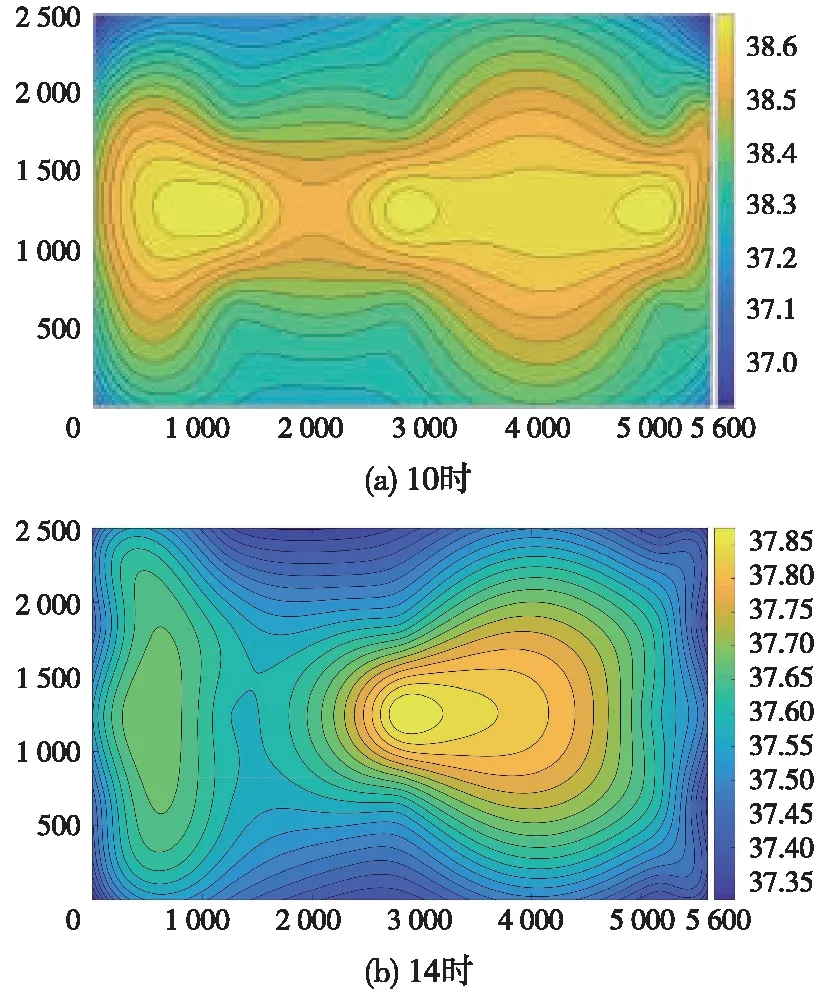
图3 轨道板底面等温线

2 无砟轨道板温度场模型的建立

2.1 温度场影响因素

根据传热学基本原理，热量传递有3种基本方式：热辐射、热传导和热对流[14](图4)。自然因素对轨道板温度场的影响，实质上是通过上述热量传递方式来实现。

图4 轨道板与环境热交换示意

任何温度高于绝对零度的物体都会向外辐射能量。与热传导和热对流不同的是，辐射换热并不需要介质。无砟轨道板吸收太阳辐射后温度增高，转而将能量辐射向天空称为长波辐射，大气又会向各个方向反射辐射，向下作用在无砟轨道道床板表面的部分称为长波逆辐射(也称大气逆辐射)，这两个辐射的差被称为有效辐射。有效辐射在无砟轨道板表面产生的热流密度可表示为[15]

qr(t)=hr[Tair(t)-T(t，0)]

(2)

(3)

轨道板表面和周围环境存在温度差时会引起对流换热，根据牛顿冷却定律[16]，以对流换热形式进入无砟轨道表面的热流密度为

qy(t)=hy[Tair(t)-T(t，0)]

(4)

式中，qy为有效辐射产生的热流密度，W/m2；hy为对流换热系数，W/(m2·℃)；当风速ν>5时，hy=7.4ν0.78，当风速ν≤5时，hy=6+4ν[17]；Tair(t)为大气温度。

选用日平均气温和日气温幅值作为气象因素变量，日气温变化过程可采用2个正弦波叠加表达式来模拟[18]，即

0.14sin2ω(t-t0-6)

(5)

太阳辐射强度对轨道板表面温度影响与其太阳高度角、纬度、昼夜时间长短、天气状况和大气透明度有关，文献[19]实际观测结果表明，太阳辐射强度随时间变化可近似服从正弦或余弦分布，并将太阳辐射采用Fourier极数表达为

Q(t)=

(6)

式中，Q0为日最大太阳辐射；Q0=1.31nQd，Qd为太阳辐射日总量(可查当地气象资料获取)，W/m2；n为日照时间比例系数，n=12/μ；μ为1天日照时长。

此外，太阳辐射并不会完全被轨道板结构吸收，一部分被反射，另一部分被轨道板结构吸收而进入轨道板结构，被吸收的太阳辐射在轨道板表面产生的热流密度可表示为

qs(t)=αsQ(t)

(7)

式中，qs为太阳辐射产生的热流密度，W/m2；αs为轨道板表面的太阳辐射吸收系数。

2.2 温度场解析解模型

根据能量守恒定律，轨道板表面吸收和辐射的热量会维持在一个动态平衡的状态，即某一时刻轨道板表面总热流密度满足以下方程[20]

qr(t)+qy(t)+qs(t)=0

(8)

将式(2)、式(4)、式(7)代入式(8)求解，可得到轨道板表面温度表达式为

(9)

我国建筑热工设计规范[21]提出混凝土结构物表面等效温度计算式

T(t，0)=Tair(t)+(αsQ(t))/hy

(10)

对比公式(9)与文献[21]计算等效温度公式可见，两公式形式基本相同，但公式(9)较文献[21]增加了中长波热辐射系数修正值hr，考虑了现实中长波有效辐射对太阳辐射的削弱作用，进一步完善了等效温度计算公式。

求解均质半无限空间一维热传导问题与其边界条件有关。当介质表面温度已知时，为第一类边界条件；当已知介质表面热能量在各点的流速时，为第二类边界条件；当仅知介质表面温度为已知周期函数时，为第三类边界条件。自然条件下的轨道结构传热问题可按第一类边界条件求解。

(1)当z=0时，边界条件

(11)

(12)

(2)当z>0时，T(z，t)≠∞，根据上述边界条件，代入到方程(1)，均质半无限空间一维热传导方程的解为

(13)

(14)

需要指出的是，本文计算模型建立的出发点是综合考虑太阳辐射、风速、气温等气象因素对轨道板温度场的影响，适用于较稳定的晴天或多云天气，对天气情况较为复杂(如阴雨天、冰雹天)不在本模型的预测范围之内。

2.3 无砟轨道板温度场解析解模型验证

为验证上述预测公式的准确性，本节将现场试验数据作为研究对象，查询当地气象资料获得气象参数(Q=2 900 W/m2，v=1.9 m/s)，代入到本文计算公式(11)～式(14)中，将轨道板表面计算温度与实测温度数据进行对比，如图5所示。

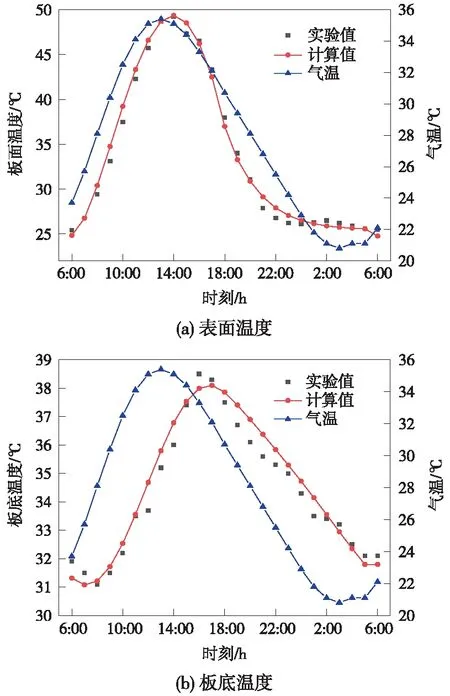
图5 轨道板计算温度与实测温度对比

由图5可见，实测轨道板表面温度25.4～49.2 ℃与计算温度24.8～49.3 ℃基本吻合，实测轨道板底面温度31.1～38.7 ℃与计算温度31.0～38.1 ℃也非常吻合。从轨道板温度梯度实测值和计算值对比(图6)，轨道板一天依次经历负温度梯度阶段(19:00～8:00，负温度梯度最大值-45.5 ℃/m)、零温度梯度阶段(19:00和8:00)、正温度梯度阶段(8:00～19:00，正温度梯度最大值75.1 ℃/m)，正负温度梯度时间段基本各占12 h。日气温最大值和正温度梯度最大值基本同时出现，下表面存在约2 h滞后。轨道板温度梯度的计算结果与实测对比结果可以看出，两者变化规律近似，计算曲线与实测曲线吻合较好。

图6 轨道板温度梯度实测值和计算值对比

为减少轨道板边界因素对数据分析的影响，选取轨道板中心13号测点各时刻轨道板温度沿深度的梯度进行讨论(图7)，轨道板结构内不同深度处温度随时间呈周期性摆动，摆动幅值随着深度的增加逐渐减小。轨道板表面日温差(25.7 ℃)远高于底部日温差(6.7 ℃)，温差变化主要集中在0～12 cm内，轨道板内温度沿深度呈非线性分布，可按指数函数进行拟合。

图7 轨道板内温度场(虚线为计算值，实线为实测值)

利用文献[11]气象参数，采用本文计算方法进行计算，计算结果如图8所示，对比结果表明：轨道板表面温度变化规律相似，变化过程都可采用正弦波或余弦波来模拟。其中，文献[11]采用三维模型，考虑了侧面的散热作用，与本文均质半无限空间一维热传导模型预测的峰值所差不大，甚至本文计算出的无砟轨道板内温度场演化峰值较文献[11]稍有超出，结果更偏于安全保守，满足极端天气频发地区工程建设需求。

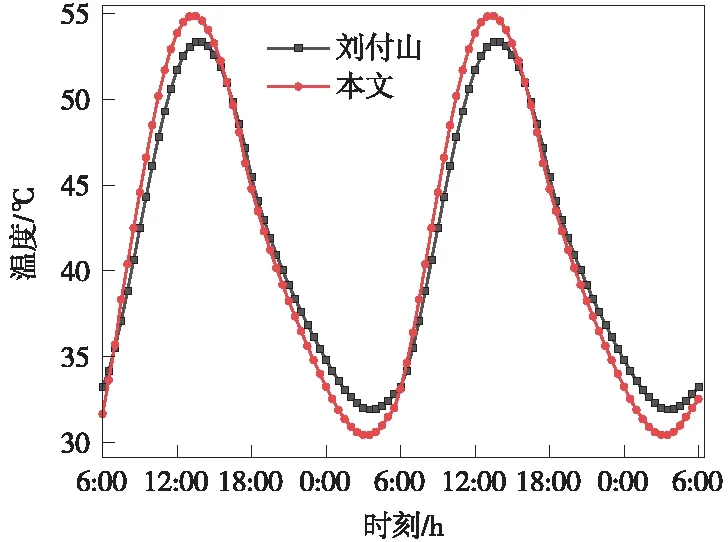
图8 轨道板表面温度计算结果对比

3 CRTSⅢ轨道板温度场及温度梯度

3.1 不同季节的轨道板温度场与温度梯度

为描述季节性温度变化同轨道板温度场演化规律的相互关系，选取当地1、4、7、10月典型月份代表四季，从气象局获取相关数据作为参考资料，以每个月中温度最高的那天作为研究对象，研究所得轨道板不同深度处温度-时间及温度梯度曲线如图9所示。结果表明：不同季节轨道板温度场及温度梯度分布规律基本相同，轨道板内温度可用正弦或余弦曲线描述，其呈周期性的变化，温度梯度在深度0～12 cm内变化较大，越靠近底部温度梯度变化越为迟缓，最大温度梯度出现的时间基本相同，但不同季节温度梯度大小存在明显的差异，最大正负温度梯度均出现在7月代表的夏季，分别为93.3 ℃/m和-44.1 ℃/m，将7月份实测数据代入所建的温度场解析解模型计算的最大正负温度梯度分别为93.8，-43.9 ℃/m，二者计算结果较为接近。

图9 四季温度-时间及温度梯度代表曲线

3.2 不同地区轨道板温度梯度建议值

轨道板设计的重要前提是既要保证轨道结构安全性和耐久性，又要考虑经济效应而不造成材料的浪费。但近几年气候变化异常，极端温度与极端天气持续时间屡破历史记录，鉴于此，从气象局查询各地区相关资料，并将数据进行一定比例放大后代入温度场解析解模型进行计算，最后将结果列于表1，该研究成果可为不同地区CRTSⅢ型无砟轨道板的设计、施工及运营维护提供参考。