双向外倾式拱塔斜拉桥施工方法优化设计研究
2022-03-22谢开仲陆伊宁梁亦登
谢开仲,陆伊宁,梁亦登
(广西大学土木建筑工程学院,南宁 530004)
引言
斜拉桥因其跨越能力强、整体刚度大、造型多样美观等优点,在交通领域得到飞速的发展和广泛的应用[1-3],斜拉桥索塔的结构形式也是日新月异。目前,常见的斜拉桥索塔结构形式有H形[4]、A形[5]、倒Y形[6]、钻石形[7]等,也出现许多造型多样的异型索塔斜拉桥[8-10]。为了达到异型索塔斜拉桥各构件的目标线形并且保证施工的安全稳定,施工的要求不断提高,施工难度加大,需要在传统施工方法的基础上进行优化。对于索塔塔柱倾斜的斜拉桥,施工首要难题在于索塔自重及施工荷载在塔柱根部产生的弯矩随着索塔不断向上浇筑会相应增大,容易导致塔柱倾斜钝角方向的拉应力超出限值[11]。若塔柱双向倾斜,两个方向的拉应力会在塔柱根部进行叠加,混凝土开裂的可能性大大增加[12],对后续施工产生不利影响。针对索塔倾斜的斜拉桥施工问题,卫军等[13]对主跨430 m的椭圆形拱塔斜拉桥4种施工方案进行比选,采用钢管横撑加斜撑的方案控制了施工应力及变形;王杰等[14]对大风环境下的H形桥塔斜拉桥采用新形式的桁架式施工横撑优化施工受力状态;张春新等[15]在A形桥塔斜拉桥主塔施工中设置了13道施加顶推力的主动横撑,保证了施工顺利进行。施工方法优化设计研究成果多针对索塔塔柱向内倾斜的斜拉桥,对于双向外倾式桥塔斜拉桥的施工方法优化设计研究较少,相关的施工控制经验技术也不多。为保障双向外倾索塔斜拉桥结构体系施工阶段的安全稳定,以某双向外倾独塔斜拉桥为例,根据斜拉桥施工受力状态分析结果,基于结构优化设计理论,建立以施工措施安全经济为目标函数的优化模型,对斜拉桥的施工方法进行优化设计,为类似结构的桥梁工程施工提供借鉴和参考。
1 工程背景
某大桥为独塔双索面预应力混凝土斜拉桥,跨度为100 m+100 m,立面布置见图1。主梁及主塔采用C60混凝土,主梁为双边主梁(Π形)截面的预应力钢筋混凝土结构;主塔塔柱高67.086 m,为实心矩形变截面,在横桥向向外倾斜5°,在纵桥向最大外倾角为11°,4根塔柱在柱顶以外倾的拱形连接,形似金花茶。拉索采用φ7 mm镀锌高强平行钢丝,为使塔柱受力对称,两根斜拉索对应两根水平索在塔柱两侧交叉锚固,全桥共40根斜拉索,40根水平索。该斜拉桥在施工时首先采用爬模法对拱塔进行分段浇筑,而后采用满堂支架现浇法建立主梁结构体系,最后分阶段进行拉索的张拉。
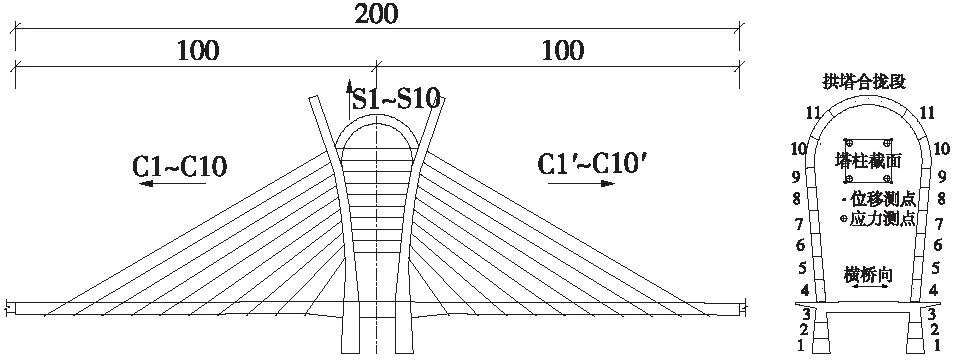
图1 主桥总体布置(单位:m)
2 斜拉桥施工过程有限元分析
2.1 有限元模型
采用Midas Civil有限元软件模拟全桥结构,如图2所示。以顺桥向为X轴,横桥向为Y轴,竖桥向为Z轴,拱塔、主梁用梁单元模拟,拉索用只受拉的桁架单元模拟;斜拉索锚固点与主梁和主塔、边主梁与横梁之间用刚臂连接;主塔支架用一般支撑模拟,约束3个方向位移;主梁满堂支架施工用只受压弹性连接模拟,主梁与拱塔刚性连接模拟。全桥共1 309个节点,2 082个单元,共设置27个施工阶段。

图2 主桥有限元模型
以拱塔第4节段到第8节段施工为例,比较有限元计算值与现场施工实测值,如图3所示。拱塔应力变形的有限元计算值与实测值十分接近,最大误差仅为5%,拱塔塔顶变形实测值比有限元计算值略小,文中建立的有限元模型可准确地确定双向外倾式拱塔斜拉桥静力性能指标,因此,该有限元模型可用于后续的施工方法优化设计分析。

图3 施工状态下拱塔的应力和位移
2.2 斜拉桥施工受力状态分析
由于拱塔是斜拉桥体系中最先承重的结构,其受力状态受到主桥施工的影响,对拱塔在主桥施工阶段中的应力及变形进行分析,得到塔柱根部拉应力及塔顶位移,如表1所示。
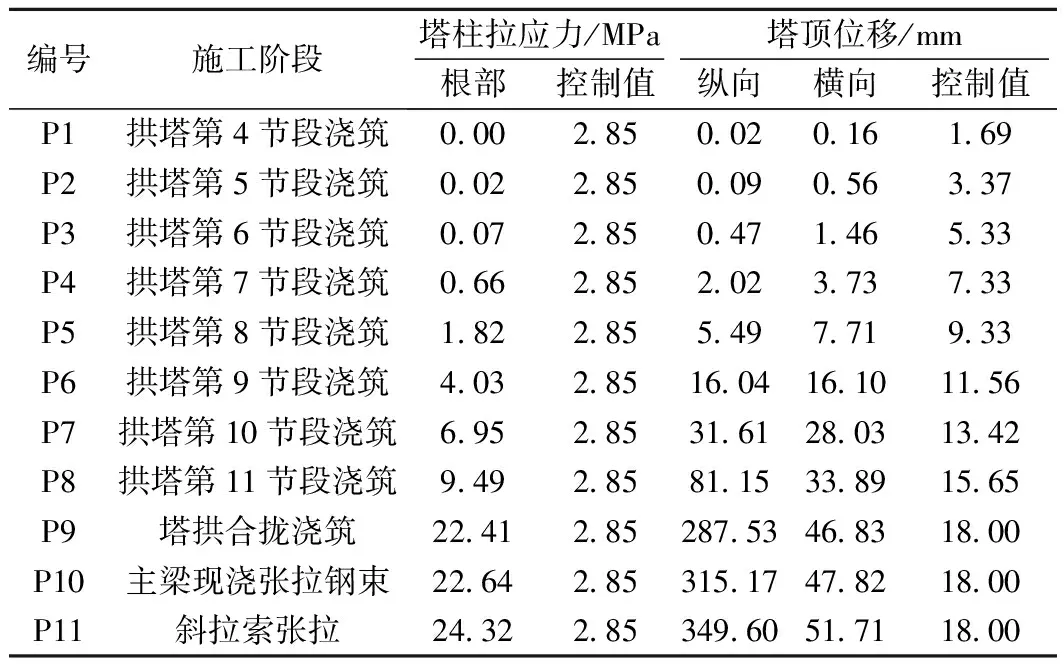
表1 拱塔施工应力变形
由表1可知,随着塔柱不断向上施工,塔柱根部的拉应力不断增加,从第6节段施工完成开始拉应力增幅不断变大。在第9节段施工完成后,塔柱根部的拉应力和塔顶位移开始超过了控制值,此时塔柱混凝土开裂的可能性及结构的安全隐患增大。若此时继续进行后续施工,塔柱拉应力和塔顶偏位将会急剧增加,在成桥后拉应力峰值达到24.32 MPa,水平位移峰值达到349.60 mm,都远远超过了控制值,斜拉桥结构的安全已得不到保障,为了保证斜拉桥施工时安全稳定,需要对斜拉桥施工方法进行优化设计。
3 斜拉桥施工方法的优化设计
3.1 优化模型
双向外倾式拱塔斜拉桥在施工过程中拱塔拉应力及塔顶偏位控制难度极大,考虑通过设置施工措施对斜拉桥施工方法进行优化。为了抵消塔柱重力和施工荷载在塔柱根部引起的过大弯矩,通过多种施工措施比选,考虑在索塔塔柱施工时在塔柱之间设置施工水平横撑。
结构优化设计的3个要素为设计变量、约束条件和目标函数[16-17]。施工横撑的优化设计以施工横撑设置的安全经济为目标函数,选取施工横撑位置、数量及结构形式作为设计变量,状态变量选取施工中塔柱根部最大拉应力、塔顶最大变形、主梁及拉索最大应力。状态变量的约束条件如下。
(1)对于两个方向都倾斜的索塔塔柱,由两个方向自重与施工荷载引起的弯矩会叠加形成附加应力。塔柱根部拉应力应满足下式要求[18]
(1)
式中,Mx、My分别为由自重及施工荷载在塔柱根部顺桥向、横桥向产生的弯矩;Yx、Yy分别为塔柱根部顺桥向、横桥向截面中性轴到受拉边缘的距离;Ix、Iy分别为塔柱根部顺桥向、横桥向截面惯性矩;N为塔柱根部所受轴力;A为塔柱根部截面面积;K为安全系数;σt为塔柱根部混凝土允许拉应力。
(2)在索塔施工过程中,由于索塔的双向倾斜,塔柱本身的自重以及施工荷载会引起塔柱的水平位移,塔顶水平位移应满足式(2)要求[19]
(2)
式中,G为根塔柱自重;F为施工荷载;l为塔柱长度;E为塔柱材料弹性模量;I为塔柱截面惯性矩;θ为塔柱倾斜角度;H为塔顶高度。
(3)在斜拉桥施工中,对主梁截面边缘混凝土的法向应力进行控制,压应力和拉应力应满足以下条件
(3)
(4)在斜拉桥施工中,拉索应均匀受力,并存在一定的安全储备,拉索强度为1670 MPa,安全系数应大于2.5。
3.2 施工措施优化设计
根据斜拉桥施工方法优化模型,通过试算、判断和再优化3个阶段对斜拉桥施工控制措施进行优化设计计算,具体计算步骤如下。
(1)根据斜拉桥施工方案和结构参数,建立有限元模型。
(2)判断斜拉桥各个施工阶段是否满足约束条件,在不满足约束条件的前一施工阶段增设一道施工横撑。
(3)对结果进行分析,若后续施工中仍不满足约束要求,则重复步骤(2)设置下一道施工横撑,直至全桥每个施工阶段都满足约束条件。
根据计算步骤进行施工横撑位置的优化设计,由于该拱塔结构在顺桥向的倾角和受力较大,首先考虑在顺桥向设置刚性横撑,以φ630 mm×8 mm钢管组成的2排桁架式结构作为初始水平横撑形式进行计算。通过3次迭代得到施工横撑设置位置,计算结果如图4所示。结果表明,拱塔顺桥向施工横撑的设置可以有效降低拱塔拉应力及塔顶纵向位移的增大幅度,使拱塔受力变化平稳,但对于塔顶横向位移的变化影响不大;在拱塔顺桥向最少设置3道施工横撑,可以将塔顶纵向位移控制在安全范围内,但塔柱拉应力及塔顶横向位移仍不满足约束条件,因此,考虑在拱塔横桥向设置施工横撑。
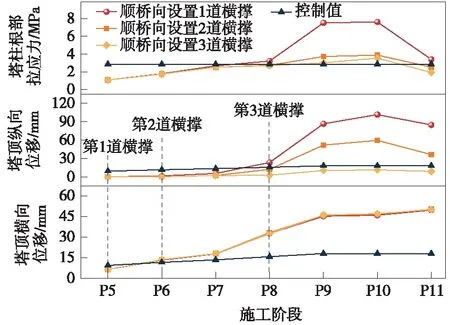
图4 顺桥向施工横撑方案计算
由于横桥向外倾角较小,考虑采用体外预应力结构消除塔柱施工的累计变形。在顺桥向施工横撑设置位置的基础上,通过两次试算得到横桥向施工横撑设置位置,计算结果如图5所示。结果表明,横桥向设置施工横撑可以有效减小塔顶横向位移和塔柱拉应力,最少需要设置两道横桥向施工横撑才能使状态变量满足约束条件。

图5 横桥向施工横撑方案计算
3.3 施工措施结构参数优化
根据索塔施工横撑的受力情况,通过改变钢管桁架式横撑的上下弦杆截面面积,对初始施工横撑结构进行优化,计算结果见图6。结果表明,随着钢管截面面积的减小,钢管应力相应增加,当钢管规格为φ273 mm×6 mm时,最大应力为216.22 MPa,超过强度设计值,则目标函数最优解为φ325 mm×6 mm钢管,此时横撑最大应力为188.51 MPa,安全系数为1.14,满足安全要求。

图6 桁架式横撑钢管截面优化
根据优化结果确定该桥施工横撑具体的结构形式,顺桥向施工横撑采用钢管桁架结构,一道施工横撑由2排桁架组成,桁架横向间隔1 m,采用I22a型钢焊接形成支撑结构,桁架上下弦杆相距1 m,采用φ325 mm×6 mm钢管,腹杆采用I22a型钢;横桥向采用体外预应力结构消除塔柱施工的累计变形。
通过对主桥进行施工方案优化计算,提出施工水平横撑设置方案,顺桥向布置如图7所示。

图7 施工横撑顺桥向布置(单位:cm)
(1)第1道施工横撑设置在塔柱在距离桥面26.5 m处,顺桥向方向设置钢管桁架水平横撑,横桥向方向设置张拉100 kN体外预应力。
(2)第2道施工横撑设置在塔柱距离桥面32.5 m处,顺桥向方向设置钢管桁架水平横撑,横桥向方向设置张拉120 kN体外预应力。
(3)第3道施工横撑设置在塔柱距离桥面44.0 m处,顺桥向方向设置钢管桁架水平横撑。
3.4 施工措施拆除顺序优化
在主梁施工完成后,需要将索塔塔柱上的施工横撑拆除。由于每道施工横撑的拆除会导致塔柱及未拆除施工横撑的内力进行重新分配[20],容易对结构产生不利影响,因此需要选择合理的拆除顺序。考虑自上而下、自下而上、由内而外、由外而内4种拆除顺序,分别进行数值模拟计算分析,分析结果如图8所示。
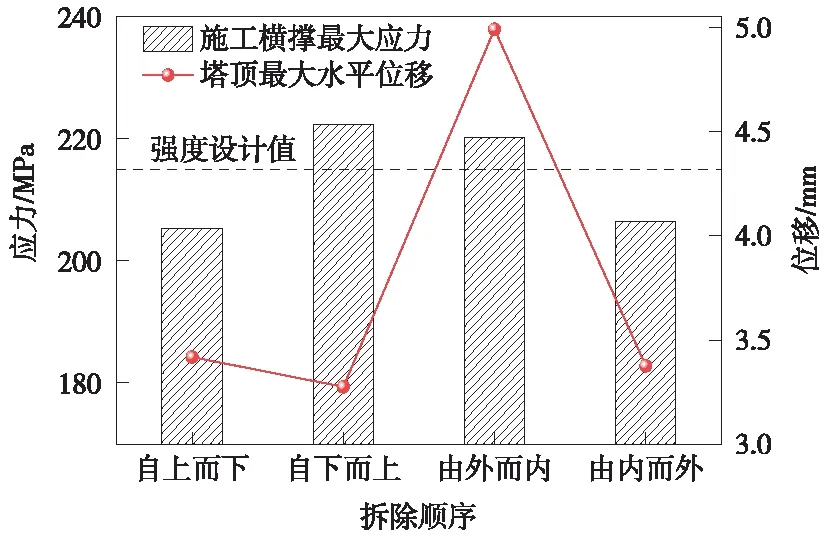
图8 施工横撑拆除顺序对比分析
结果表明,当采用自下而上的拆除顺序时施工横撑的应力最大,为222.32 MPa,超过了钢材强度设计值;采用自上而下的拆除顺序时,施工横撑的应力最小,为205.37 MPa,自上而下的拆除顺序对施工横撑的内力重新分配产生的不利影响更小,并且在拆除后塔顶变形值为3.42 mm,处于安全范围之内,因此,自上而下的施工横撑拆除顺序更为合理。
4 施工方法优化结果及实测验证
4.1 拱塔施工受力状态
该桥施工方法优化前后拱塔应力及位移的有限元计算结果如图9所示,在斜拉桥施工方法优化前,塔柱根部的拉应力和塔顶偏位随着分段浇筑的不断向上而急剧增加,施工方法优化后,拉应力与位移曲线变化平缓,并且塔柱根部拉应力峰值从24.32 MPa降低至1.67 MPa,降低约93%,塔顶最大水平位移从349.60 mm控制在14.50 mm,降低约96%,皆处于控制范围之内。表明该施工优化方法可以使拱塔在施工过程中受力更为均匀,线形变化稳定,具有减小拱塔根部应力集中以及控制塔顶偏位的作用。

图9 施工方法优化前后拱塔受力状态对比
将优化后的斜拉桥施工方案应用于该桥实际施工中,对拱塔内力和线形进行监测,实测数据与有限元计算数据如图10所示。实测值与计算值吻合,变化趋势一致,应力误差在5%之内,表明该优化后的施工方案在实际施工中应用效果良好。

图10 施工优化后拱塔受力实测值与计算值
4.2 主梁及拉索施工受力状态
在拱塔分段浇筑完成后,主梁通过支架现浇法进行施工,对主梁截面边缘混凝土的法向应力进行控制。通过有限元计算得到主梁在各个施工阶段时截面最大拉应力为0.96 MPa,出现在与拱塔底部固结的位置,小于规范限值3.28 MPa;最大压应力为20.34 MPa,位于纵梁变截面处,小于规范限值24.26 MPa,满足安全要求。
采用刚性支承连续梁法得到的目标成桥索力作为初张力按施工过程进行正装迭代,得到的索力作为斜拉索初张力。通过有限元模拟得到施工阶段中拉索的最大应力如图11所示。由主塔向边跨的斜拉索拉应力呈现增大趋势,在C10和C10′达到最大,同时水平索拉应力在S8达到最大。在施工过程中拉索应力呈现平缓的变化趋势,拉索受力均匀。在斜拉桥施工阶段中拉应力峰值位于斜拉索C10和C10′,最大拉应力为560.3 MPa,则安全系数为2.98,大于规范规定安全系数2.5,满足安全储备要求。

图11 施工过程中拉索最大应力
5 结语
为了消除双向外倾式拱塔斜拉桥在施工阶段存在的安全风险,保证施工顺利进行,基于结构优化设计理论,提出了设置施工措施的斜拉桥优化施工方法。根据有限元仿真分析和实际施工监控结构得到如下结论。
(1)基于结构优化设计理论对斜拉桥施工方法进行优化设计,通过迭代计算得到斜拉桥最优施工方法为在拱塔施工中设置3道施工措施,顺桥向采用钢管桁架式水平横撑,横桥向张拉体外预应力。
(2)有限元计算结果表明,优化后的斜拉桥施工方法有效地将拱塔最大拉应力控制在1.67 MPa,塔顶最大水平位移控制在14.50 mm,斜拉桥施工受力状态变化平稳且满足安全要求,可以达到目标成桥状态。
(3)在采用优化后的施工方法进行斜拉桥施工过程中,拱塔施工应力的实测值与有限元计算值较为接近,最大误差为5%,表明该方法对该桥实际施工起到了科学有效的指导作用。
