大跨度斜拉桥钢锚梁空间复杂力学性能研究

祝 兵，张子怡，张 振，宋 凡，齐 乐

(西南交通大学土木工程学院，成都 610031)

斜拉桥作为一种拉索体系，跨越能力更大，并且建筑高度小、施工方便安全、桥型美观，因此成为近年来我国大跨度桥梁中应用最普遍的一种桥型之一。对于斜拉桥来说，其拉索的锚固结构是保证桥梁安全的重要结构，并且其设计必须达到传力可靠、安全耐久、造型美观、易于维护的基本要求[1-3]。目前工程中常见的锚固区结构形式主要有钢锚箱结构和钢锚梁结构[4-6]。其中传统的钢锚梁结构因造价低、施工简单便捷等优点被广泛应用[7]。钢锚梁的主要功能是将斜拉索局部的集中力安全、均匀地传递到塔柱。钢牛腿是钢锚梁的支撑结构，是主要的竖向受力构件。由于受到拉索较大的集中拉力作用，锚固结构部位会出现明显的应力集中现象[8-10]。

本文钢锚梁结构由顶板、单腹板和底板焊接而成，采用牛腿结构实现钢锚梁与混凝土的连接。本文的计算方法考虑了施工阶段、牛腿顶板与锚梁底板之间的摩擦作用和预应力作用对钢锚梁结构的影响。并通过采用有限元软件对钢锚梁在不同工况下的空间力学特性进行计算分析，确保钢锚梁各部分结构受力安全，从而为后续施工设计和类似工程提供理论依据。

1 工程背景与有限元模拟

1.1 工程背景

该大跨度斜拉桥主桥孔跨布置为(72+212+560+212+72)m，为双塔双索面组合梁斜拉桥。主梁采用混凝土面板下设两小纵梁的结构形式，主塔采用菱形索塔，过渡墩、辅助墩采用空心薄壁墩，均采用群桩基础。斜拉索采用高强度低松弛平行镀锌钢丝索，全桥共176根，标准索距15 m。

1.2 有限元软件及参数

采用三维空间分析软件对塔顶钢锚梁节段建立有限元模型，为简化计算，选取索力最大的塔顶钢锚梁作为研究对象。材料参数及荷载参数的选用如下。

混凝土塔柱采用C50混凝土，弹性模量为3.45×104MPa，泊松比为0.2，密度取2 500 kg/m3；钢锚梁采用Q345钢材，弹性模量为2.05×105MPa，泊松比为0.3，密度取7 850 kg/m3；预应力采用钢绞线施加，抗拉强度标准值为1 860 MPa，弹性模量为1.95×105MPa，泊松比为0.3，密度取7 850 kg/m3。

混凝土的强度标准值及设计值和钢材的强度设计值分别见表1、表2。

表1 混凝土的强度标准值和设计值 MPa

表2 钢材的强度设计值 MPa

表1中，fck、ftk分别为混凝土抗压、抗拉强度标准值，fcd、ftd分别为混凝土抗压、抗拉强度设计值。

1.3 计算荷载取值及施加

钢锚梁承受的荷载主要为以下三类，模型荷载加载位置如图1所示。

图1 模型荷载加载位置

(1)横梁结构自重(自重系数取-1)。

(2)斜拉索索力荷载(取值见表3)。

(3)预应力荷载(大小为1 395 MPa，预应力钢筋面积取1 688 mm2)。

根据全桥计算模型，提取塔顶最不利荷载组合下的索力值见表3，斜拉索尾索索力采用3D单元面压力的方式施加。

表3 斜拉索索力值 kN

1.4 有限元模型及边界条件

采用三维空间分析软件建立了钢锚梁模型，钢结构部分采用尺寸8 mm的空间四面体单元模拟，混凝土部分利用映射网格方法采用8～100 mm 的空间四面体单元模拟。

钢锚梁有限元模型底部采用固结约束，以塔根顶面中心位置建立参考点，并把顶面所有节点(从属节点)与参考点(主节点)之间进行刚接；侧面采用对称约束，模型中共1 200 859个单元，267 163个节点。有限元模型如图2所示，边界条件如图3所示，钢锚梁尺寸及构造如图4所示。

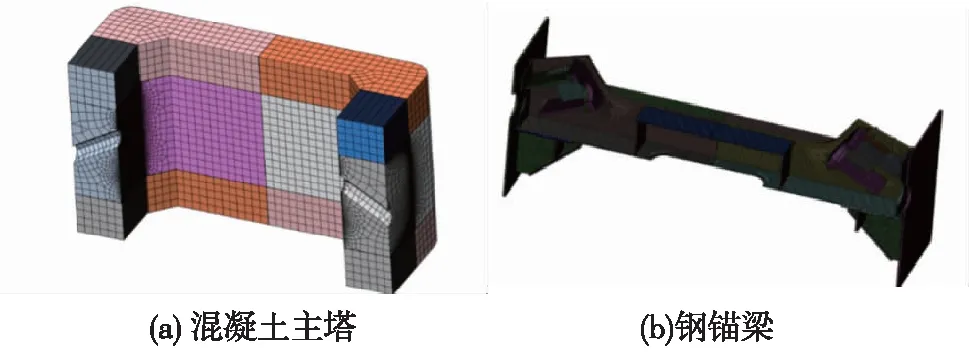
图2 有限元模型

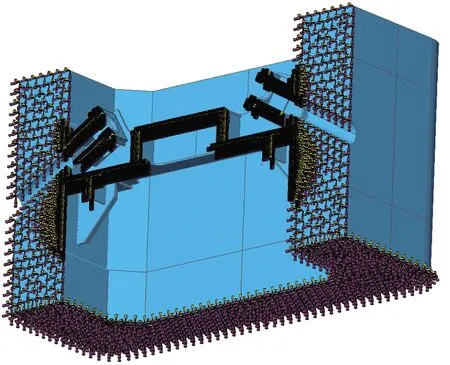
图3 有限元模型边界条件

图4 钢锚梁几何尺寸(单位：mm)

2 钢锚梁空间复杂力学性能分析

为了得出钢锚梁最不利受力状态，建立了3种工况进行分析，分别为考虑预应力的线性分析、考虑预应力的非线性分析、不考虑预应力的非线性分析。

2.1 线性分析

考虑预应力钢筋的作用，并使用线性分析计算方法，各接触面采用共节点方式连接，牛腿顶板与钢箱底板之间拉开0.5 mm间距，用来模拟连接单元，利用仅受压弹性连接来模拟成桥阶段牛腿顶板与锚梁底板之间的高强螺栓连接。整个工况共分为3个施工阶段：成桥阶段、运营阶段、断索阶段。

成桥阶段在对称面上施加对称约束，桥塔混凝土底部采用固定约束。左侧牛腿顶板与钢箱底板设置仅受压连接与边缘部分焊接，右侧牛腿顶板与钢箱底板设置仅受压连接。

运营阶段施加运营索力，并将仅受压一侧边缘焊接，利用弹性连接中的刚接单元进行模拟。

断索阶段是为了考虑桥梁运营期间突发的一侧断索情况，采用在前面2个施工阶段上钝化一侧索力来模拟。

2.2 非线性分析

为了考虑成桥阶段采用高强螺栓连接牛腿顶板与钢锚梁底板时的摩擦作用，采用一般接触来模拟两者之间作用，摩擦系数设为0.03，并且考虑预应力的作用，进行非线性分析。

2.3 力学性能分析

各工况应力云图如图5、图6所示(混凝土主压应力云图以线性分析成桥阶段工况为例)。

图5 成桥阶段混凝土主压应力线性分析结果(单位：MPa)

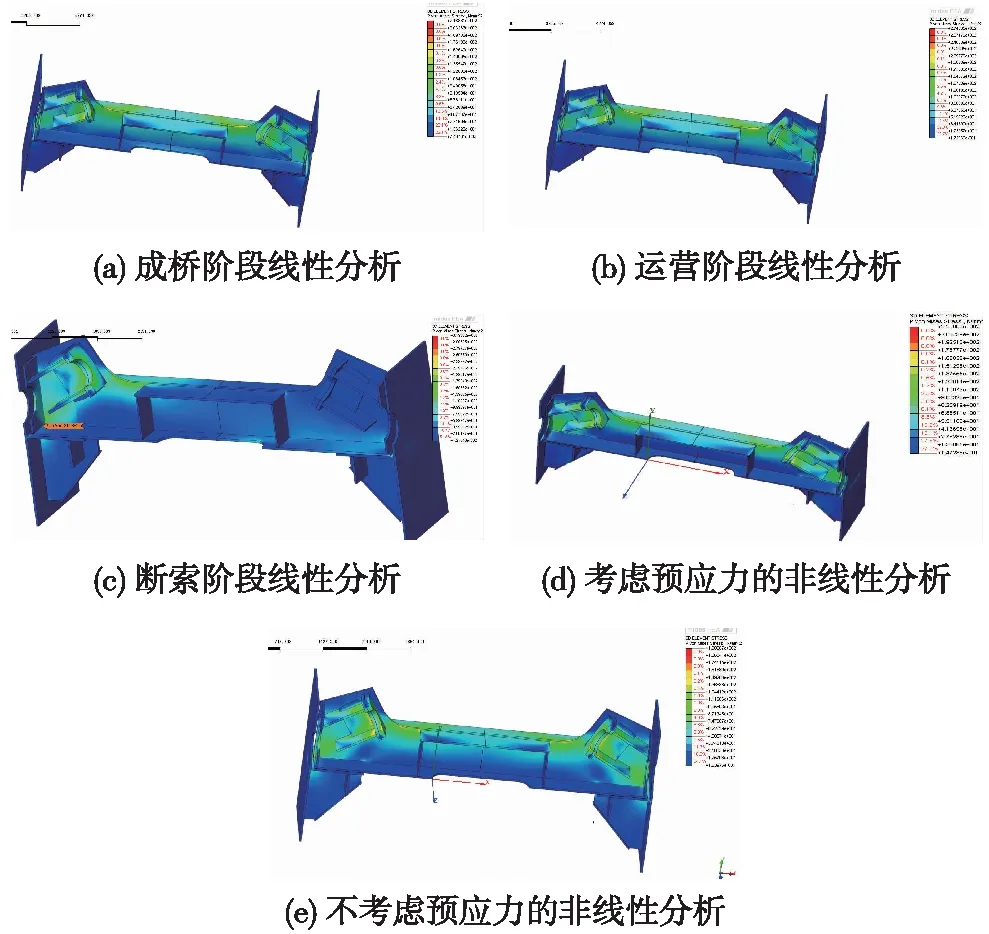
图6 钢锚梁等效应力结果(单位：MPa)

由图5可以看出，混凝土主压应力在牛腿顶板与锚梁底板、牛腿壁板三者角点处较大，存在应力集中现象。

由图6可以看出，钢锚梁腹板与钢锚梁底板交界角点处、锚垫板角点处存在较大应力，牛腿腹板与钢锚梁焊接角点部位存在应力集中现象。对于塑性较好的材料，当承受稳定压力或重复次数很少的荷载时，局部应力对安全影响甚小，只要结构大面积上的应力仍处于弹性状态，局部应力过高就不会直接导致结构破坏。

各工况应力结果如表4、表5所示。

表4 线性分析方法等效应力最大值 MPa

表5 非线性分析方法等效应力最大值 MPa

断索工况下混凝土主压应力较大位置集中于未断索一侧牛腿顶板附近混凝土区域。分析原因为由于另一侧松开，失去水平方向力，导致未断索一侧水平力增大。

由表4、表5及图7、图8可知，在模拟出牛腿顶板与钢锚梁底板之间的摩擦作用后，钢锚梁等效应力最大值为214 MPa，略大于线性分析的应力结果176 MPa。应力较大区域基本都位于相同区域即钢锚梁的腹板与底板角点处。牛腿顶板最大应力为203 MPa，与线性分析的应力结果135 MPa相比，牛腿顶板最大应力增大约50%。

图7 钢锚梁结构等效应力对比

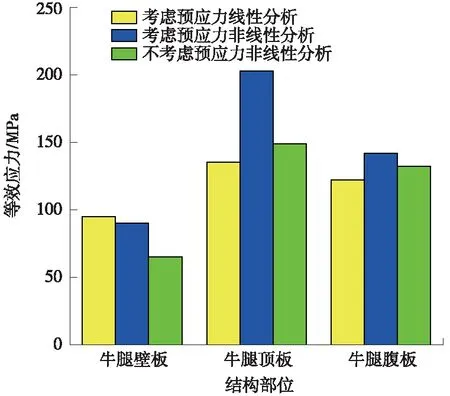
图8 牛腿结构等效应力对比

不考虑预应力情况下在模拟出成桥阶段牛腿顶板与钢锚梁底板之间的摩擦后，钢锚梁等效应力最大值为180 MPa，与考虑预应力非线性分析时钢锚梁等效应力最大值214 MPa相比，应力值减小。应力较大区域也都位于相同区域即锚梁腹板与锚梁底板焊接角点处。

3 结论

以某特大斜拉桥为工程背景，对索塔锚固区钢锚梁结构进行了多工况受力计算分析，得出以下结论。

(1)本文重点针对成桥阶段牛腿顶板与钢锚梁底板之间的摩擦作用对牛腿顶板应力影响大小进行分析，通过线性分析与非线性分析结果的对比，发现考虑摩擦作用后牛腿顶板应力增大了约50%。为保证结构安全，在对钢锚梁受力进行分析时不可忽略牛腿顶板与钢锚梁底板之间的摩擦作用。

(2)考虑预应力作用的非线性分析得到的钢锚梁结构及牛腿结构的等效应力均大于不考虑预应力作用的非线性分析得到的钢锚梁结构及牛腿结构的等效应力，牛腿顶板应力增长最为明显，增大约36%。为保证结构安全，在对锚固区计算分析时应考虑预应力的作用。

(3)通过对运营工况和断索工况下分析结果的对比，断索工况下混凝土的主压应力明显增大，且牛腿顶板的应力较运营工况增大约40%，设计时应考虑不平衡索力的影响，加强焊缝设计，保证结构的安全性。

(4)在3种工况作用下，钢锚梁腹板与底板焊接角点处、牛腿壁板与顶板及腹板焊接部位均存在应力集中现象，属于受力薄弱部位，实际施工及运营过程中应加强对薄弱部位的检测。