基于机器视觉的卷烟燃烧轴向偏离校正方法研究

岳 翔

（中国电子科技集团公司第四十一研究所，安徽 蚌埠 233010）

1 引言

卷烟燃烧后的包灰情况是评价卷烟质量的重要因素之一[1]，烟支在阴燃[2]时水平放置，其燃烧端的灰柱由于重力作用，会沿重力方向偏离原来的未燃烧烟支所在的空间轴线方向。这就造成了烟支燃烧灰柱的偏离，并且由于“视觉问题的病态本质：随着视点的变化，物体的二维外观会变化很大”[3]，在空间中平行于烟支轴线观察的机器视角平面所观察的烟支灰柱尺寸以及偏离角度都是有所不同的。因此在视点变化的情况下，为了客观地描述灰柱偏离，采取了一种基于机器视觉的卷烟燃烧轴向偏离校正方法。

2 视觉偏差分析

根据灰柱偏离度的定义[4]可知，烟支燃烧灰柱与烟支滤棒轴心的最大偏离角度是灰柱偏离度。取空间中某一机器视角的二维平面观察卷烟燃烧灰柱与烟支滤棒轴心的相对位置以及角度关系。如图1所示，以卷烟燃烧过程中实时移动的炭线作为灰柱与滤棒的分界线，已燃烧的部分为灰柱，未燃烧的部分为滤棒。首先根据卷烟燃烧灰柱边界拟合出一条灰柱拟合轴心线，通过计算出滤棒轴心线与灰柱拟合轴心线的夹角α获得灰柱偏离角度。

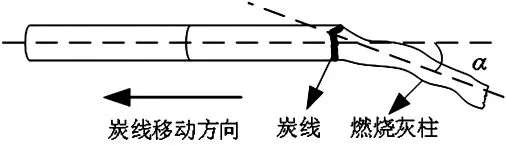
图1 卷烟燃烧灰柱示意图

但是，在机器视觉观察的过程中，机器视觉所处的空间位置和滤棒轴心线与灰柱拟合轴心线形成的平面所在空间的相对位置不固定，正是这种不确定性，导致分析灰柱偏离度过程中出现了视觉偏差。且机器视觉检测的灰柱偏离度随着相对位置的移动，在同步发生变化。

如图2所示，摄像机拍摄平面S0，与卷烟滤棒和其燃烧灰柱形成的平面S1平行，在此情况下，所检测的灰柱偏离度是实际没有偏差的数值。但当摄像机与卷烟的空间相对位置发生变化时，由于视觉偏差的影响，在摄像机拍摄平面S0′采集图像检测的灰柱偏离度发生变化，如图3所示，由原来的α变为α′，这就造成了卷烟滤棒轴心与卷烟燃烧灰柱拟合轴心之间的夹角出现了视觉偏差。

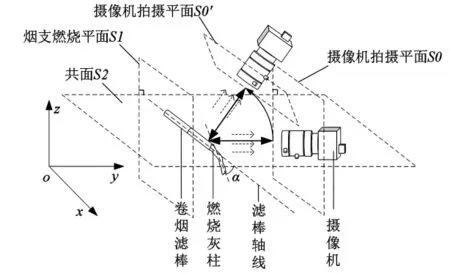
图2 视角平面位置分布示意图

图3 视场平面变化前后的灰柱偏离角度示意图

3 校正原理

随着机器视觉检测视点位置的移动，出现了视觉偏差，导致了卷烟燃烧过程中灰柱偏离度的数据检测错误。因此，在无法保证灰柱偏离度能正确测量的情况下，需要对出现的视觉偏差进行校正。

3.1 建立简化模型分析

如图4所示，为分析简便，将卷烟滤棒简化为BE线段，将卷烟燃烧灰柱简化为BC线段，相机视场平面简化为S0和S0′，置于笛卡尔空间直角坐标系中建模分析[5]。卷烟燃烧灰柱受到重力作用，与滤棒轴心处于同一平面S1。以经过燃烧灰柱的最低点（C点）且垂直于S1的平面为xoy平面，建立空间直角坐标系。以o点为一个顶点，x，y，z轴正方向为此顶点的三条边建立一个长方体模型，使烟支整体置于长方体进行分析，各参数定义如下：其中，BE为卷烟滤棒；BC为卷烟燃烧灰柱；BC′为在机器视角平面投影的灰柱；AB为卷烟燃烧灰柱BC沿BE延长线上的投影；平面S1是卷烟燃烧灰柱与滤棒轴心所处的平面；平面S0与S0′是机器视角平面，平面 ABD′C′即为 S2，与 S0′平行；平面 S1 与 S2 的夹角为 γ；平面 CDD′C′垂直于平面 ABD′C′；α 是 BC与卷烟滤棒BE延长线的实际夹角；α′是在机器视角平面ABD′C′的灰柱BC′与卷烟滤棒BE延长线的夹角。

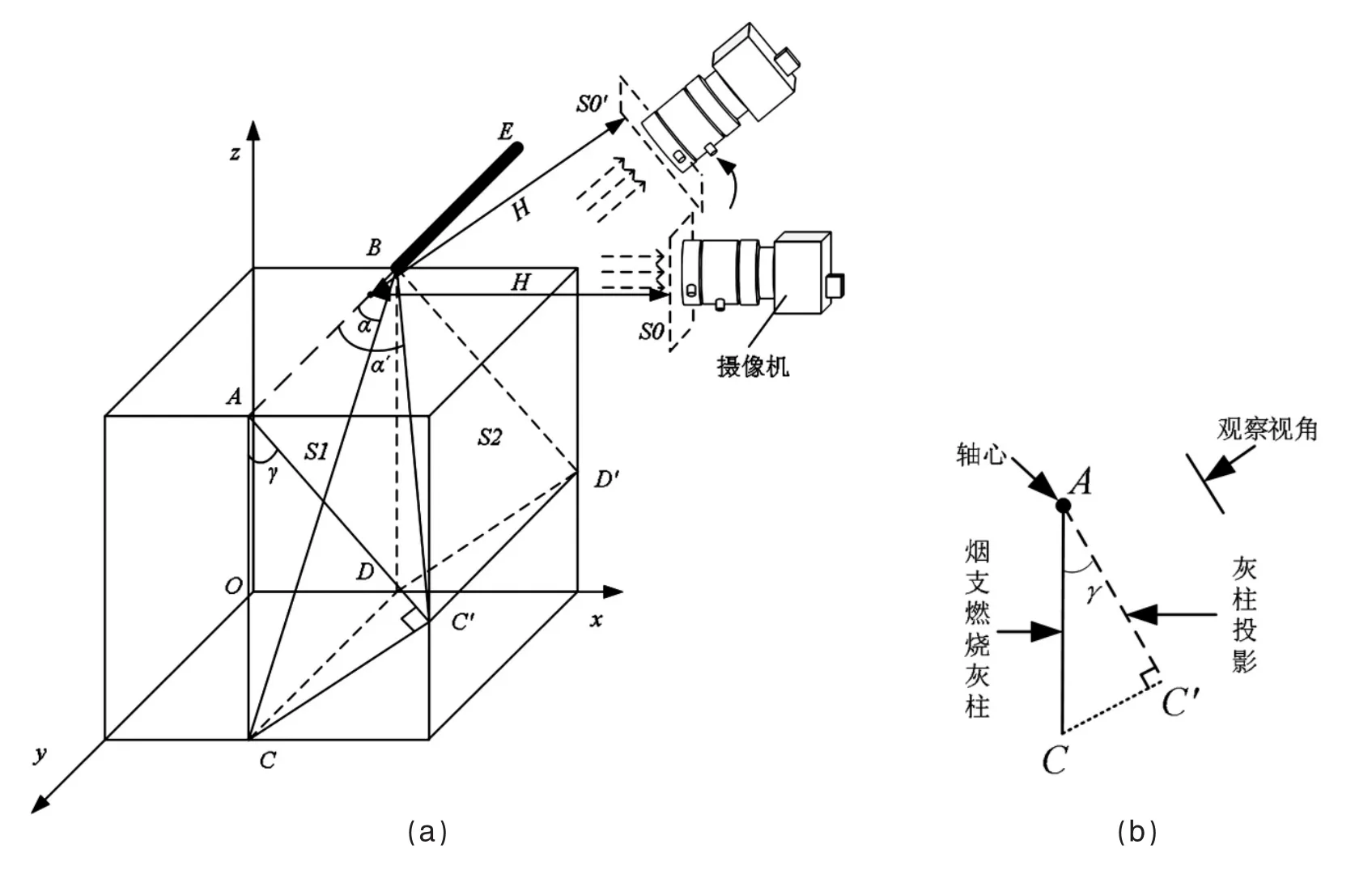
图4 卷烟燃烧简化分析示意图

当机器视角平面S0与卷烟滤棒及灰柱所在的平面S1平行时，且卷烟滤棒和灰柱整体的重心与机器视觉视场重心在同一水平面时，机器视觉测得的灰柱与卷烟滤棒夹角为实际的灰柱偏离度，否则，在围绕卷烟滤棒轴心旋转的任意角度位置，机器视觉所测得的灰柱偏离度均存在视觉偏差。如图4所示，当机器视觉的视场平面处于S0′位置时，灰柱偏离度随着视点的变化也发生了偏差，由实际的α变为α′。在利用机器视觉测量时，为了便于获得二者之间的关系，计算实际的灰柱偏离度，采用投影的方式[6]，将S1平面内的卷烟滤棒与卷烟燃烧灰柱投影于和机器视觉的视场平面S0′平行的平面S2。根据投影关系，分析计算实际角度值与实际灰柱长度值。

3.2 投影校正

如图4所示，AB为卷烟燃烧灰柱BC在卷烟滤棒轴心线上的投影。在卷烟滤棒与卷烟燃烧灰柱投影于视场平面S0′的过程中，为便于分析各参数之间的关系，以AB为卷烟滤棒及灰柱所在的平面S1与投影平面S2的相交线，过灰柱BC在水平面的投影CD，作平面CDD′C′垂直于投影平面S2，则BC在投影平面S2上的投影为BC′，且CC′垂直于BC′。由此构成三个直角三角形，即△ABC，△ABC′，△ACC′，利用直角三角形的三角函数关系，推导计算相关参数之间的关系公式。

在已知平面S1和S2夹角为γ、机器视场平面ABD′C′的灰柱BC′及其与卷烟滤棒BE延长线的夹角α′的情况下，计算出实际灰柱长度与灰柱偏离度。对于校正方法，在数学模型空间中，问题简化为已知 α′，γ，BC′，求 α，BC。

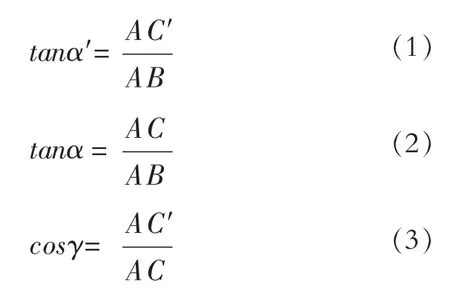
联立（1）（2）（3）三式，可以得到 α 与 α′和 γ 的关系如公式（4）所示

联立（5）和（6）两式，可以得到公式（7）：

联立（4）和（7）两式，可以得到灰柱长度BC与BC′，α′，γ 的关系如公式（8）所示。

由上述公式分析可知，在某个γ角度下的单个平行于卷烟轴心的视角平面进行校正计算时，由于受到观察视角的局限，当时，不能通过提出的校正方法进行校正。但是当同时有两个或者两个以上不同γ角度下的平行于卷烟轴心的视角平面（两个平面不平行或重合）进行检测校正时，即使某一个平面满足条件：当kπ（k=0,1,2···），也能由另一个平面检测得到的数据进行校正计算，从而获得实际的校正值。

4 实验分析

4.1 建立仿真模型

利用SolidWorks软件进行仿真，建立在卷烟燃烧过程中，灰柱受重力影响产生在重力方向和卷烟组成的平面内的偏离滤嘴轴心情况的模型，如图5所示。

图5 卷烟燃烧灰柱偏离情况的Solidworks仿真图

根据实际的烟支尺寸，设定卷烟直径7.2mm，滤嘴长为58mm，卷烟燃烧的灰柱长为30mm。为了实验数据的对比分析，设定已知的灰柱偏离卷烟轴心角度值 α0=30°。

4.2 校正对比分析

对模型进行以卷烟轴心为中心的旋转，采用多种γ视角平面，进行在视场平面上对卷烟燃烧灰柱轴向偏离角度的实际测量，并与采取理论公式校正的值作对比。已知轴向偏离角度值α0=30°，分别选择具有代表性的 γ 角度为 0°，30°，45°，60°，90°以及120°，进行分析并统计对应的 α′与 L′，经过公式校正的α与L值。具体如表1所示。

表1 不同γ角度的轴向偏离角度及长度测量的校正对比

从表1中可知，在6组不同的γ视角测得的轴向偏离角度值α′，经过公式校正后，得到的6组校正轴向偏离角度α均与已知的理论值α0保持一致，误差不超过0.01°，这是由于在校正公式的计算过程中采用的数据保留小数点后的位数影响的。并且经过分析可以看出，在0≤γ＜90°范围内，随着γ角度的增大，视场平面观察到的烟支燃烧灰柱偏离卷烟滤嘴轴线的角度在减小，测量得到的灰柱长度也在减小。这是因为随着γ视角的增大，夹角与灰柱长度在视场平面内的投影都在减小，如图4（b）的简化示意图所示。当γ角度增大到90°时，视场平面与烟支沿重力方向和卷烟组成的平面垂直。此时校正公式不适用，需结合其他视角的视场平面采集数据校正。在90°＜γ≤180°时，在视场平面内的投影角度及投影灰柱长度变化，与（180°-γ）角度视场检测得到的数据变化一致，具体变化情况如曲线图6所示。曲线图6中x代表γ角度值，y代表视场平面内的投影角度或投影灰柱长度。γ从-90°开始到0°之间，视场平面内的投影角度及投影灰柱长度由最小值逐渐递增到最大值；从0°开始到90°之间，视场平面内的投影角度及投影灰柱长度由最大值逐渐递减到最小值，呈现类似于余弦曲线的变化趋势。

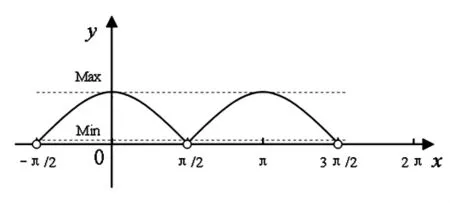
图6 轴向偏离的投影角度及灰柱长度随γ变化曲线示意图

5 结语

作为评价卷烟质量及性能的一个重要参考指标，燃烧灰柱偏离卷烟轴线的角度起到至关重要的作用。由于物体随视点的变化会出现视觉偏差，因此校正这种视觉偏差以获得准确的灰柱偏离角度就成为关键环节。提出的卷烟燃烧轴向偏离校正方法，在平行于卷烟轴线的任意角度的视场平面（除重合面外）观测情况下，根据视觉校正公式，能直接校正机器视觉观测到的灰柱偏离角度和灰柱长度值，得到实际的数值，从而能作为准确客观地评价不同品牌卷烟的质量及性能的重要参考指标。

提出的卷烟燃烧灰柱轴向偏离校正方法还存在局限性，实际的卷烟燃烧灰柱不仅受到重力作用影响垂直向下偏离卷烟轴线，还受风力等其他作用的影响产生偏离，研究内容在理想仿真情况下验证了校正方法的准确性与可行性，为卷烟燃烧轴向偏离校正提供了理论依据。