基于LASSO算法的光谱变量选择方法研究

王恺怡，杨 盛，郭彩云，卞希慧，3*

（1.天津工业大学 省部共建分离膜与膜过程国家重点实验室，化学工程与技术学院，天津 300387；2.绍兴市柯桥区污染物总量控制中心，浙江 绍兴 312030；3.宜宾学院 过程分析与控制四川省高校重点实验室，四川 宜宾 644000）

由于具有快速、无损、绿色等优点，光谱分析技术已广泛应用于食品、石油化工、医疗和农业等领域的复杂样品分析［1］。其中建立一个准确、稳定的多元校正模型是光谱分析技术直接分析复杂样品的关键。由于光谱中变量数通常大于样本数，并且有些变量与预测组分无关，这可能降低模型的预测能力［2］。因此，在建模前需采用变量选择去除无关变量的影响以提高模型的预测性能［3－7］。

最小绝对收缩与选择算子（LASSO）是Tibshirani［8］提出的一种收缩估计方法。该方法在回归系数绝对值之和小于一个常数的情况下，使残差平方和（RSS）最小化，这意味着某些回归系数会被缩小为零，从而达到变量选择的目的。LASSO变量选择在生物信息学和化学计量学领域得到了越来越多的关注［9－13］。基于LASSO的优点，本文将其引入到复杂样品的光谱定量分析中。首先利用LASSO对两组复杂样品的光谱进行变量选择，然后采用偏最小二乘（PLS）［14］和多元线性回归（MLR）建立模型，并与无信息变量消除－PLS（UVE－PLS）［15］、蒙特卡罗结合无信息变量消除－PLS（MCUVE－PLS）［16］和随机检验－PLS（RT－PLS）［17］进行比较。结果表明，基于LASSO的变量选择方法计算时间短，选择变量少且保持了较好的预测性能。

1 实验部分

1.1 算法原理

LASSO在普通最小二乘（OLS）函数的基础上引入一范数正则化（L1）惩罚项来约束RSS，即在回归系数的绝对值小于某个常数的条件下使RSS最小化。假设X=[x1，x2，…，x m]T∈Rm×p，y=[y1，y2，…，y m]T∈Rm×1和β=[β1，β2，…，βp]T∈R p×1，其中T表示矩阵的转置，X、y和β分别是光谱、目标值和回归系数，m和p分别表示样本数和变量数。已知X和y，求β，构成线性回归问题：y=X×β+ε。它通常由OLS求解，优化目标函数如下：

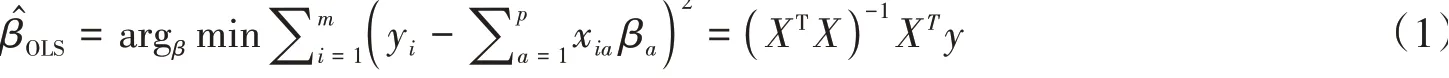
-1表示矩阵的逆。在光谱分析中，变量个数通常远远大于样品个数，即p≫m，这将使(XTX)-1不可求。定义LASSO的公式为：

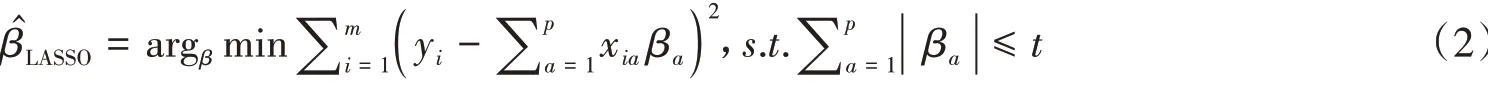
其中t为调优参数。公式（2）等价于公式（3）：

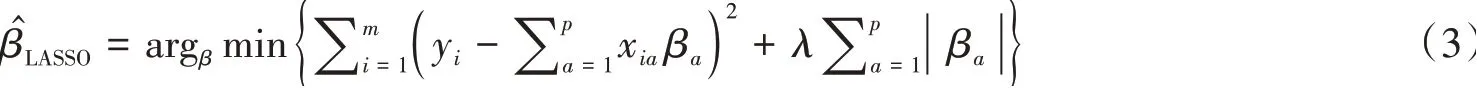
假设XTX+λΩ-为非奇异矩阵，方程的解为：

参数λ需预先确定，它控制着回归系数中零的数量。但在实际中很难确定λ的最佳值。Efron等［18－19］提出了用于快速求解LASSO的最小角回归（LARS）算法。该算法通过前向梯度（Forward stagewise）策略寻找最佳变量集合，最初设定所有回归系数都为0，每次迭代加入或删除一个变量。LARS中的最佳模型位置s为重要参数，s为0表明无变量被选择，s为1表示选择了最大的变量数。通过采用交叉验证寻找模型的最佳位置s。LARS算法不仅解决了寻找最佳λ值的困难且提高了计算效率。因此，本研究采用LARS算法实现LASSO变量选择。采用10折交叉验证和Sp准则［18］确定最佳模型位置s以及回归系数。

1.2 实验数据

本文选择了两组复杂样品的光谱数据集验证LASSO方法的有效性。数据集1是50个三元调和油样品的近红外光谱数据。光谱使用近红外（NIR）分光光度计（TJ270－60，天津市拓普仪器有限公司）采集，波长范围为800～2 500 nm，采样间隔为1 nm，共1 701个波长点。分析组分为香油、大豆油和稻米油。以香油的含量为目标组分，采用Kennard－Stone（KS）方法对50个样品数据进行划分，训练集样品33个，预测集样品17个。训练集的近红外光谱如图1A所示。

图1 三元调和油的近红外光谱图（A）及生物样品的拉曼光谱图（B）Fig.1 NIR spectra of ternary blend oil samples（A）and Raman spectra of bio-fluid samples（B）

数据集2是文献中90个生物样品的拉曼光谱数据［20］。采用RP－1 Raman Identification System（美国印第安纳州，西拉法叶，普渡研究园区Spectra code Inc.公司）拉曼光谱仪测定。拉曼光谱的采集曝光时间为25 s，波数范围为2 636.3～473.6 cm－1，采样间隔约为5 cm－1，共有422个波长点。分析组分是人体尿液中含有的8种重要代谢物。本文以肌氨酸含量为研究对象。采用KS分组方法对90个样品数据进行划分，训练集样品60个，预测集样品30个。训练集的拉曼光谱如图1B所示。

2 结果与讨论

2.1 最佳模型位置s的确定

通过LARS实现LASSO的变量选择，第一步确定最佳模型位置s。首先设置s取值范围为0～1，将其划分1 000段，间隔0.001，采用10折交叉验证计算每个s下的RSS，即每个s得到10个RSS，取10个RSS的平均值得到最终的RSS。共计算了1 000个s下RSS的平均值，并采用Sp准则，确定最佳模型s的位置。图2A、B分别显示两个数据集的1 000个s下RSS的平均值以及标准差随s的变化图。

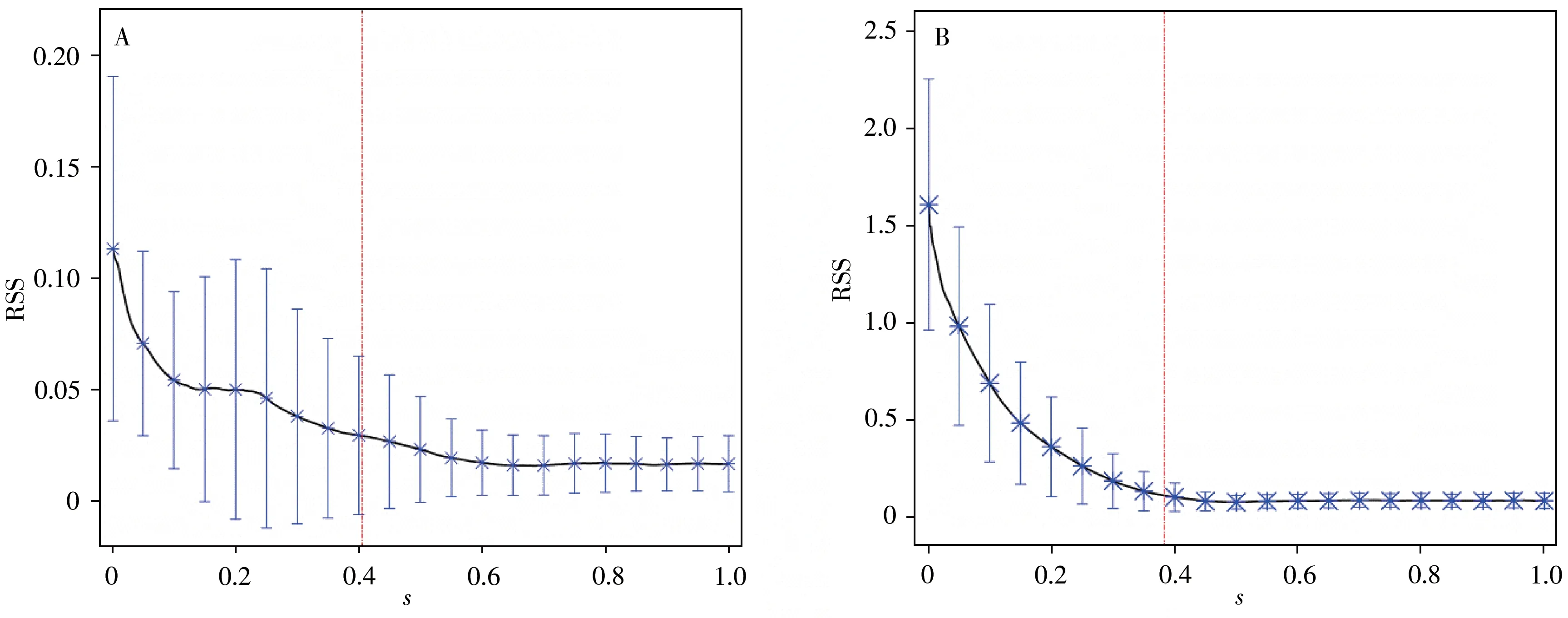
图2 数据集1（A）和数据集2（B）的RSS随着1 000个s值的变化图Fig.2 Variation of RSS with 1 000 s values for dataset 1（A）and dataset 2（B）the solid line represents the average value of 10 RSS obtained by 10-fold cross-validation for each s value，the asterisk and short vertical line indicate the average values and standard deviations of RSS at each 50 s values（实线表示每个s值进行10折交叉验证得到的10个RSS的平均值，星号和短竖线表示每隔50个s值处RSS的平均值以及标准差）

从图2A、B可看出，当s值为0时，RSS的均值最大。随着s的增大，RSS的均值逐渐下降，后趋于平缓。10折交叉验证的标准差也随s值的增大逐渐变小。数据集1的标准差大于相同s值对应的数据集2的标准差。通过S p准则选择最佳模型对应的s值，如图中虚线所示，数据集1和数据集2的最佳s值分别为0.405和0.383。

2.2 LASSO的β系数分布

通过10折交叉验证和S p准则得到最佳模型位置，选择最佳位置进行LASSO变量选择得到β系数。图3A、B分别显示数据集1和2进行LASSO选择变量后的β系数分布。从图3A可看出，对于数据集1，大多数的β系数均为0，说明LASSO方法具有很好的数据稀疏性。β值不为零的系数值虽大小不一，但这些非零的变量均将被选择，与数值大小无关。对于数据集2，从图3B中可得到相似结论，该数据集选择的变量主要集中在1 300～500 cm－1范围内。

图3 数据集1（A）和数据集2（B）的LASSO的β系数分布Fig.3 Distribution ofβcoefficients in LASSO for dataset 1（A）and dataset 2（B）

2.3 不同变量选择方法保留变量的分布

为了更好地考察LASSO变量选择方法保留变量的分布情况，数据集1和2的训练集平均光谱和保留的变量分别显示在图4A、B中。作为对比，UVE、MCUVE和RT 3种变量选择方法保留的变量也显示在图中。

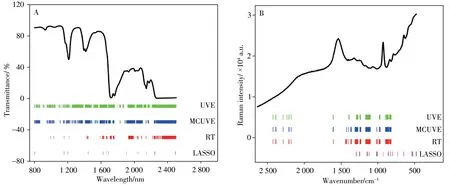
图4 数据集1（A）和数据集2（B）4种变量选择方法保留变量的分布图Fig.4 Distribution of retained variables by the four variable selectionmethods for dataset 1（A）and 2（B）

从图4A可以看出，对于数据集1，UVE保留的变量最多；MCUVE保留的变量数目和UVE相比有所减少，但在UVE的变量范围内；RT保留的变量在UVE和MCUVE保留变量的范围内进一步减少；LASSO则在RT保留的变量范围内进一步减少变量。从图4B可以看出，对于数据集2，UVE、MCUVE和RT保留的变量数相差不大且位置相似。LASSO保留的变量最少，变量所在的位置与其他3种变量选择方法有部分重叠。结果表明LASSO保留变量的位置与其它变量选择方法基本一致，且保留的变量更少。

2.4 不同方法的结果比较

为了验证LASSO的变量选择方法效果，在LASSO变量选择后分别建立了MLR和PLS模型，并与PLS、UVE－PLS、MCUVE－PLS、RT－PLS进行比较。6种方法的保留变量数、RMSEP、R和运行时间列于表1。其中保留变量数表明模型的简单程度，RMSEP和R值用于衡量模型的预测准确度，运行时间衡量模型的运算效率。

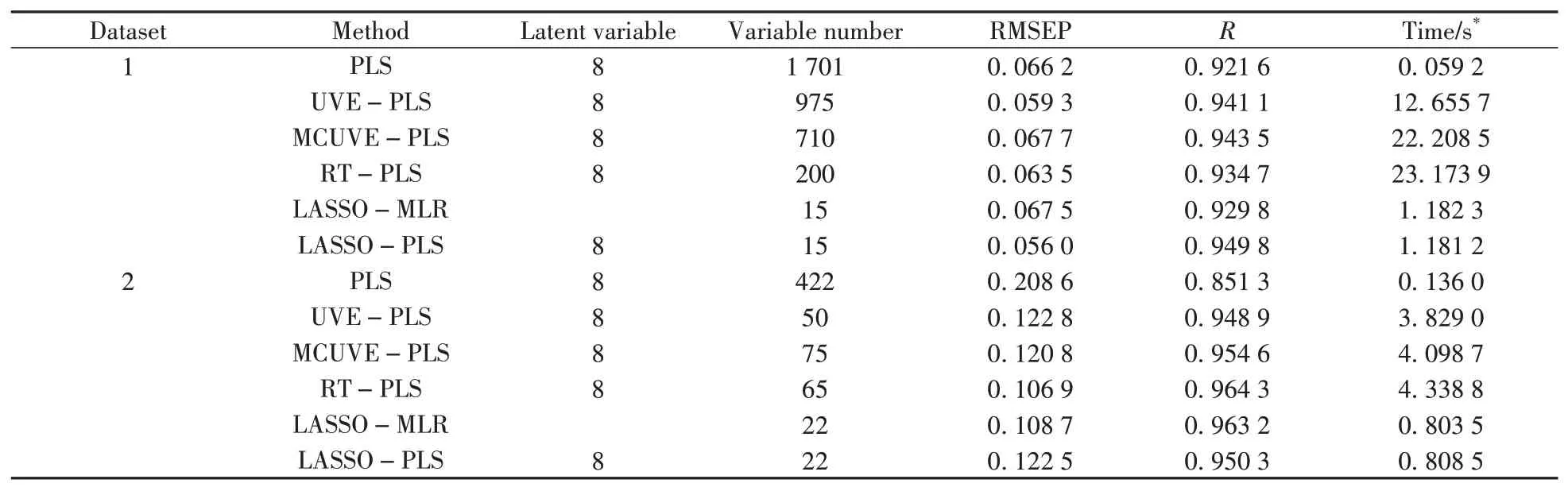
表1 两个数据集的不同建模方法的结果比较Table 1 Result comparison of different modeling methods for the two datasets

从表1可以看出，对于数据集1，UVE、MCUVE、RT和LASSO 4种变量选择方法保留的变量数依次减少。其中LASSO保留的变量数最少，仅15个，少于数据集1训练集的33个样品数。因此LASSO变量选择后可建立MLR模型。与全波长的PLS相比，进行UVE、RT和LASSO变量选择后建立的PLS得到的RMSEP小于PLS，且R值大于PLS，说明这3种变量选择方法均可提高PLS模型的预测准确度，其中以LASSO－PLS的预测准确度最高。而LASSO变量选择后建立MLR模型的预测准确度比LASSO－PLS差，PLS由于无变量选择的步骤，因此其计算效率最高。LASSO－PLS、LASSO－MLR的计算效率比UVE、MCUVE、RT快1个数量级。因此，对于数据集1，综合保留变量数、预测准确度及运算效率，LASSO－PLS的性能最佳。

对于数据集2，UVE、MCUVE和RT 3种变量选择方法保留的变量均较少，预测准确度明显优于PLS，且计算时间不超过5 s，说明这3种变量选择方法的效果良好。LASSO－MLR和LASSO－PLS能进一步减少保留的变量，提高计算效率及PLS的预测准确度，其中以LASSO－MLR的预测准确度最高。两个数据集的结果均表明，基于LASSO的变量选择方法保留的变量数更少，计算效率高且能提高PLS模型的预测性能。

3 结论

本文利用两个复杂样品的近红外和拉曼光谱数据集探究了基于LASSO的变量选择方法在光谱变量选择中的性能，并与PLS、UVE－PLS、MCUVE－PLS和RT－PLS方法在保留变量数、预测性能和运算效率上进行比较。结果表明，与其他3种变量选择方法相比，基于LASSO的变量选择方法不仅计算时间短，使用变量数少，还可以得到更高或者相当的预测准确度。因此，LASSO算法有望广泛应用于光谱的变量选择。