不同结构二氧化碳水合物热物性的分子动力学模拟

李元超 焦丽君 尹晓霞 李 倩 华泽珍

（青岛职业技术学院海尔学院 青岛 266555）

0 引言

气体水合物是在一定的温度和压力条件下形成、由水分子和客体分子组成的包络状固体化合物，水分子之间由氢键相连形成笼形结构，客体分子位于晶穴中心。常见的客体分子有甲烷、乙烷、丙烷和二氧化碳等。根据客体分子大小，通常分为结构I 型、II 型和H 型水合物。自然界中如天然气水合物、二氧化碳水合物一般是I 型水合物，客体分子尺寸为4-5.5 Å；人工合成的水合物如环戊烷水合物、四氢呋喃水合物通常是II 型水合物，客体分子尺寸为6-7 Å；构成H 型水合物的大客体分子尺寸为8-9 Å，H 型水合物相对较少[1]。气体水合物的结构不同，对应的热力学性质，如相平衡特性有较大的区别，相比于二氧化碳水合物的相平衡条件（276.45-282.05K，1.81-3.83MPa），二氧化碳和环戊烷二元水合物的相平衡条件更加温和（281.55-290.25K，0.15-1.92MPa）[2]，具体表现在相平衡温度更高、压力更低，能够克服二氧化碳水合物合成压力高、过冷度大的问题，使基于二氧化碳水合物的碳捕集、海水淡化以及空调蓄冷的低成本应用成为可能[3-7]。因此，研究不同结构水合物的热物性对于水合物合成和分解的应用具有重要意义。

气体水合物的热物性测量有实验和模拟两种方法，目前研究较多的是甲烷水合物，其次是乙烷、丙烷和四氢呋喃水合物，二氧化碳水合物及二元水合物的热物性报道较少[8-13]。实验室人工合成的水合物通常具有晶格缺陷和空穴，Lee 等[14]用X 射线衍射方法测试了二氧化碳和环戊烷（CP）二元水合物的晶体结构和晶穴占有率，发现结构为II 型水合物，由于二氧化碳的存在，晶格常数相比于环戊烷水合物略有增加，其中环戊烷完全占据了大晶穴，二氧化碳占据了62%的小晶穴。实验测量热物性对于实验设备的要求比较高，而且很难精确的合成不同结构和不同晶穴占有率的水合物，因此，本文采用分子动力学模拟的方法研究不同结构和晶穴占有率下气体水合物的热物性。

1 模型与方法

1.1 分子模型

利用Material Studio 建立不同结构的气体水合物，结构类型和大小晶穴占有率如表1所示，初始构型如图1所示，分别为I 型CO2水合物和II型CO2-CP 二元水合物，其中二氧化碳占据小晶穴，环戊烷占据大晶穴，图1（b）是晶穴占有率为100%的情况。I 型水合物结构为2X·6Y·46H2O，II 型水合物结构为8X·16Y·136H2O，其中X 表示大晶穴，Y 表示小晶穴[1]。为了保证体系原子数大致相同，I 型水合物采用3×3×4 超晶胞结构，II 型水合物采用2×2×3 超晶胞结构，水分子数分别为1565和1632，晶穴数均为288。按照Takeuchi 等[15]提出的I 型和II 型水合物的晶胞常数及绝对坐标，分别放置氧原子和氢原子，并将客体分子放在晶穴中心。水分子、二氧化碳分子和环戊烷分子分别选择SPC/E 模型、EMP2 模型和全原子力场模型，势能函数见表2[16-18]。分子间相互作用力包括Lennard-Jones 范德华力和库仑力，见公式（1），不同原子间的Lennard-Jones 势能作用遵从Lorentz-Berthelot 作用规则，见公式（2）和（3）[19]。

表2 势函数参数Table 2 Potential energy parameters

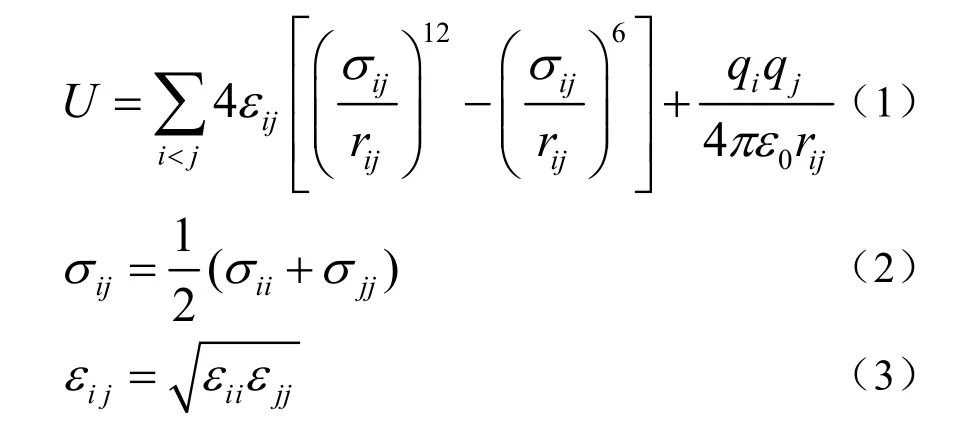
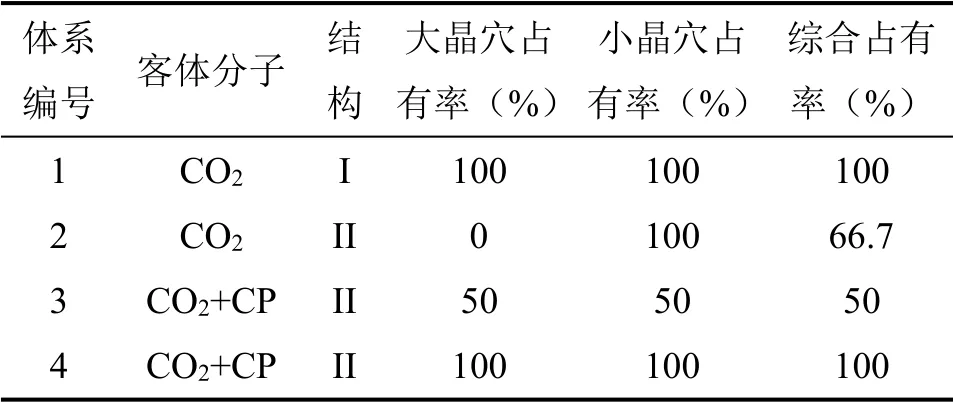
表1 模拟体系Table 1 Simulation system

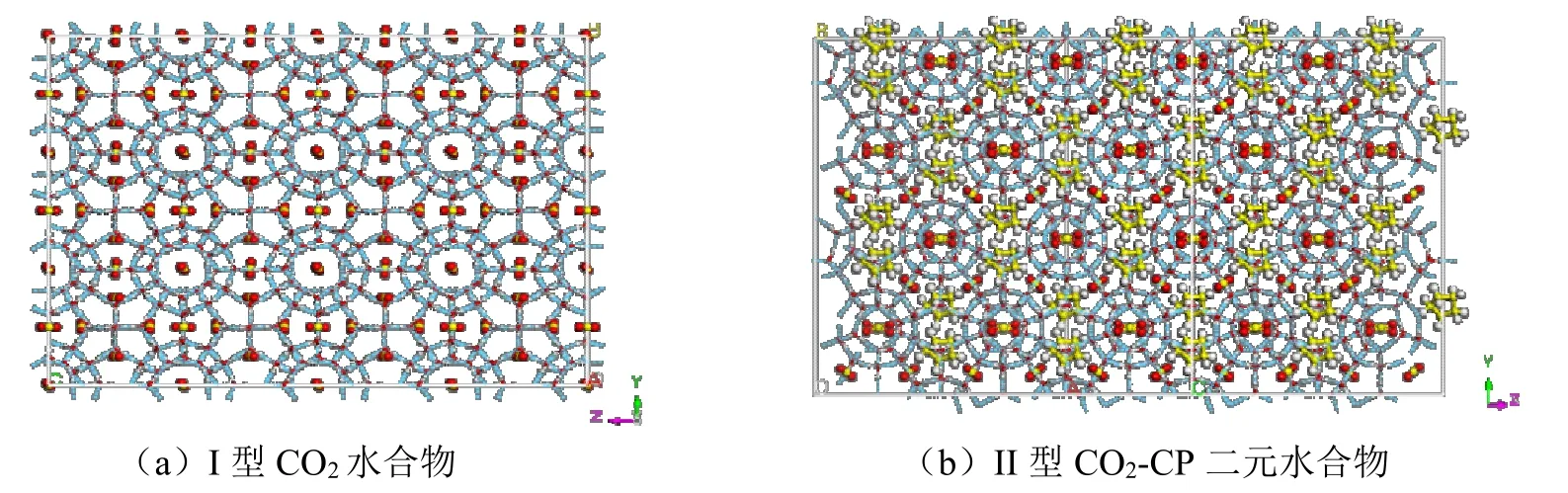
图1 初始构型（蓝线-氢键，棒状-共价键，球形-原子，氧原子-红色，氢原子-白色，碳原子-黄色）Fig.1 Configuration of initial hydrate（The dotted blue line represents hydrogen bonding,the ball represents atom,the stick represents covalent bond,C-yellow,O-red,H-white）

1.2 模拟方法

采用开源软件LAMMPS 进行分子动力学模拟。三个方向均采用周期性边界条件，时间步长为1fs，分子间相互作用力的截断半径为12Å，采用PPPM（particle-particle particle-mesh）方法计算长程静电力，精度为10-6，采用velocity-verlet 积分算法求解运动方程，采用shake 算法固定水分子的键长和键角。首先进行能量最小化，然后将体系置于NVT系综下运行500ps，采用Noose-Hoover 热浴，阻尼系数设为0.1ps，使体系达到恒定温度并保持平衡。接着将体系置于NPT 系综下运行500ps，采用Noose-Hoover 热浴和压浴，温度阻尼系数设为0.1ps，压力阻尼系数设为1ps，使体系达到设定温度和压力。最后，将体系置于NVE 系综下运行1ns。模拟结束后，采用平衡分子动力学模拟（EMD）方法，运用Green-Kubo 公式，编程计算热导率，见公式（4）[20]。

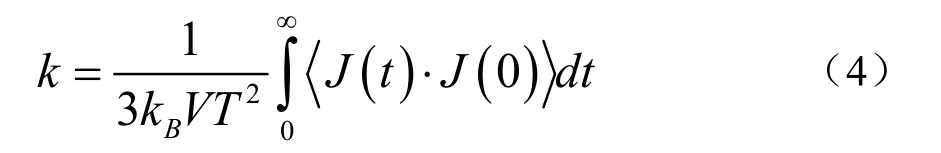
其中，kB为波尔兹曼常数，J/K；V为模拟区域的体积，m3；T为模拟区域的温度，K；＜J(t)·J(0)＞为热流自相关函数（HCACF）。

声子平均自由程是影响物体内部热输运的重要参数[21]，李佳等[22]通过对甲烷水合物的分子动力学模拟发现，分解过程的固-液界面厚度与甲烷水合物内部的声子平均自由程十分接近，说明水合物的导热特性对水合物分解过程影响较大。根据分子动力学理论，声子平均自由程的计算方法如公式（5）所示[23]。

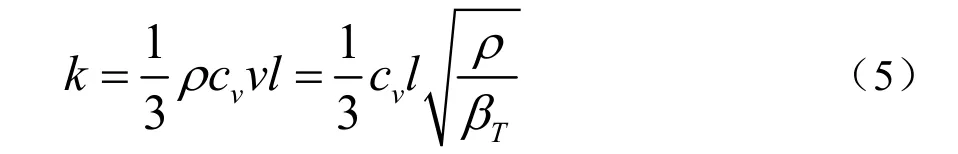
其中，k为热导率，W·m-1·K-1；ρ为密度，kg/m3；βT为等温压缩系数，m·s2/kg；ν为声学速度；，kg/s；cν为等容比热，kJ/kg·K。以上参数均可以通过分子动力学模拟求解，密度取NPT 系综下的统计平均值，等温压缩系数计算方法如公式（6）所示，在0.5ns 的NPT 系综下计算系统体积的波动。

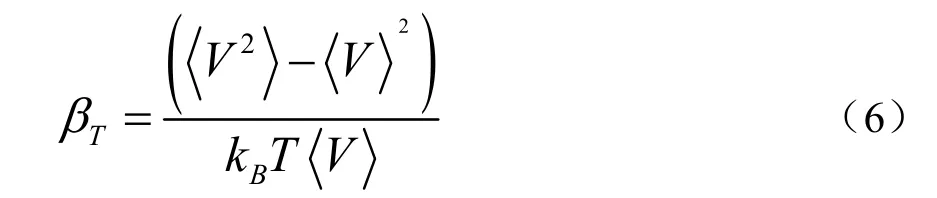
其中，V表示体系的体积，m3，T为体系温度，K，kB为波尔兹曼常数，大小为1.38×10-23J/K。此外，等容比热cν根据NVT 系综下能量波动计算，见公式（7），其中E为体系的势能，J/mol。

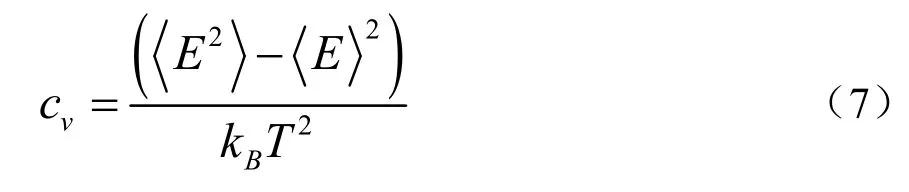
为了验证模拟方法和计算方法的正确性，测试计算了I 型CO2水合物的热物性，在相似的热力学条件下，模拟值与文献值相接近，具体对比将在结果与讨论部分展开。

2 结果与讨论

2.1 I 型CO2 水合物导热特性

200K、20MPa 条件下，CO2水合物在模拟初始时刻和结束时刻的径向分布函数如图2所示，可以看出，水分子和二氧化碳分子之间均存在明显的结构分布，水中氧原子之间的径向分布函数峰值依次出现在2.73Å，4.5Å和6.46Å，分别代表了水合物晶格结构五元环边长和多面体笼形结构中水分子与对角水分子之间的距离，二氧化碳分子中碳原子之间的径向分布函数峰值出现在6.76Å，代表了两个晶穴中心的距离，峰值与文献报道一致[24]，证明了水合物结构的正确性。而且在模拟前后，水合物的结构峰值并未发生变化，只是略有下降，这是由于在分子间力的作用下，水分子和二氧化碳分子在初始位置上振动和旋转导致的，水合物结构并未发生变化，证明了二氧化碳水合物在200K、20MPa条件下处于热力学稳定区域，可以使用平衡分子动力学模拟方法（EMD）获得热物性。图3 是I 型CO2水合物在200K、20MPa 条件下的热流自相关函数（HCACF）和热导率随关联时间变化曲线，可以看出，热流在0.6ps 内快速收敛，热导率也在1ps 内趋于稳定，平均热导率为0.8498W·m-1·K-1。姚贵策[25]通过实验测得的二氧化碳水合物的热导率在0.45-0.53W·m-1·K-1（温度范围257.15K-273.15K），Jiang 等[26]通过分子动力学模拟测得的二氧化碳水合物的热导率在0.75-0.95W·m-1·K-1（温度范围0-250K），热导率与实验和模拟结果均处于同一数量级，证明了模拟方法的可靠性。

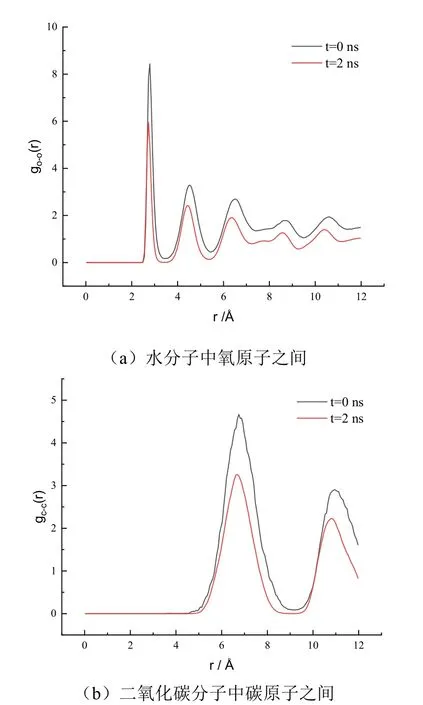
图2 200K，20MPa 条件下不同时刻径向分布函数图Fig.2 RDF plots of atoms at different time under 200K,20MPa

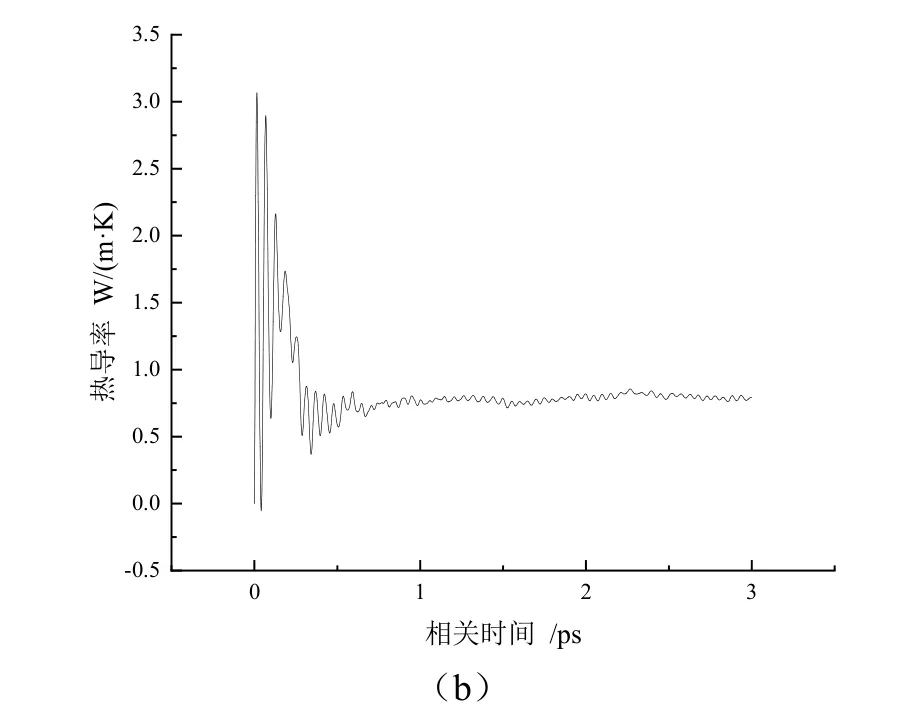
图3 200K,20MPa 条件下（a）热流自相关函数（b）热导率随关联时间变化Fig.3 (a)HCACF and(b)thermal conductivity varies versus time under 200K,20MPa

图4 是热流自相关函数能谱，通过对热流自相关函数作傅里叶变换得到，能够反映出声子能量的消散。可以看出不同频率的声子对水合物内部热输运的影响不同，高频成分（＞15THz）大于低频成分，说明在水合物导热过程中高频声子（15-25THz）起到主导作用，而低频声子（＜12THz）幅值相对较小，表明在低频区域主客体分子之间充分耦合，而高频区域的声子更容易消散，即声学声子的导热对水合物导热起主导作用。I 型二氧化碳水合物的声子作用模式和甲烷水合物相类似[23]。

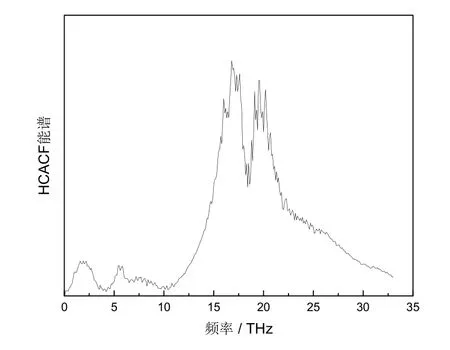
图4 二氧化碳水合物热流自相关函数能谱Fig.4 Power spectra of HCACF in CO2 hydrate

2.2 II 型CO2-CP 二元水合物导热特性及对比分析

在200K、20MPa 条件下，计算II 型CO2-CP二元水合物在模拟前后的径向分布函数，结果表明，模型正确而且水合物处于热力学稳定区。热流自相关函数和热导率分别在1ps 和1.5ps 结束收敛，说明模拟方法对于II 型CO2-CP 二元水合物同样具有适用性。由于篇幅限制，此处不再展示，主要分析热导率以及影响水合物热导率的声子输运模式。图5 是不同条件不同结构水合物的热导率，可以看出，对于I 型水合物，热导率的模拟值均大于实验值[25-27]，热导率随温度变化不存在显著的正相关或负相关趋势，对于不同的水合物，表现为在一定的温度范围内热导率随温度升高，而在另一范围热导率随温度降低。

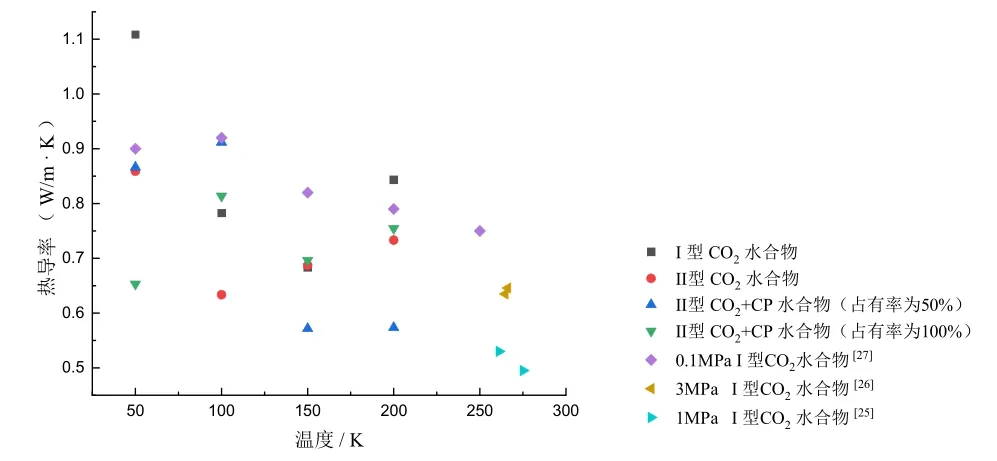
图5 二氧化碳水合物热导率Fig.5 Thermal conductivity of carbon dioxide hydrate

为了分析不同结构二氧化碳水合物的导热特性，图6 绘制了20MPa、200K 条件下II 型CO2水合物（a）和II 型CO2-CP 水合物（晶穴占有率为50%（b）和100%（c））的热流自相关函数能谱。可以看出，影响II 型水合物的声子导热模式除了高频声子外，低频声子区域（＜12THz）也存在明显的峰值，而且当二氧化碳仅占据小晶穴时，低频声子区域的能谱峰值较低，随着环戊烷分子占据大晶穴，能谱峰值提高，当二氧化碳和环戊烷完全占据大小晶穴时（晶穴占有率100%），低频声子区域的能谱峰值最高，几乎接近于高频声子区域的能谱峰值。说明对于II 型水合物，随着大晶穴的晶穴占有率的增加，低频声子导热对水合物导热起到的作用也变得显著，高频声子和低频声子导热均对水合物导热起到重要作用。

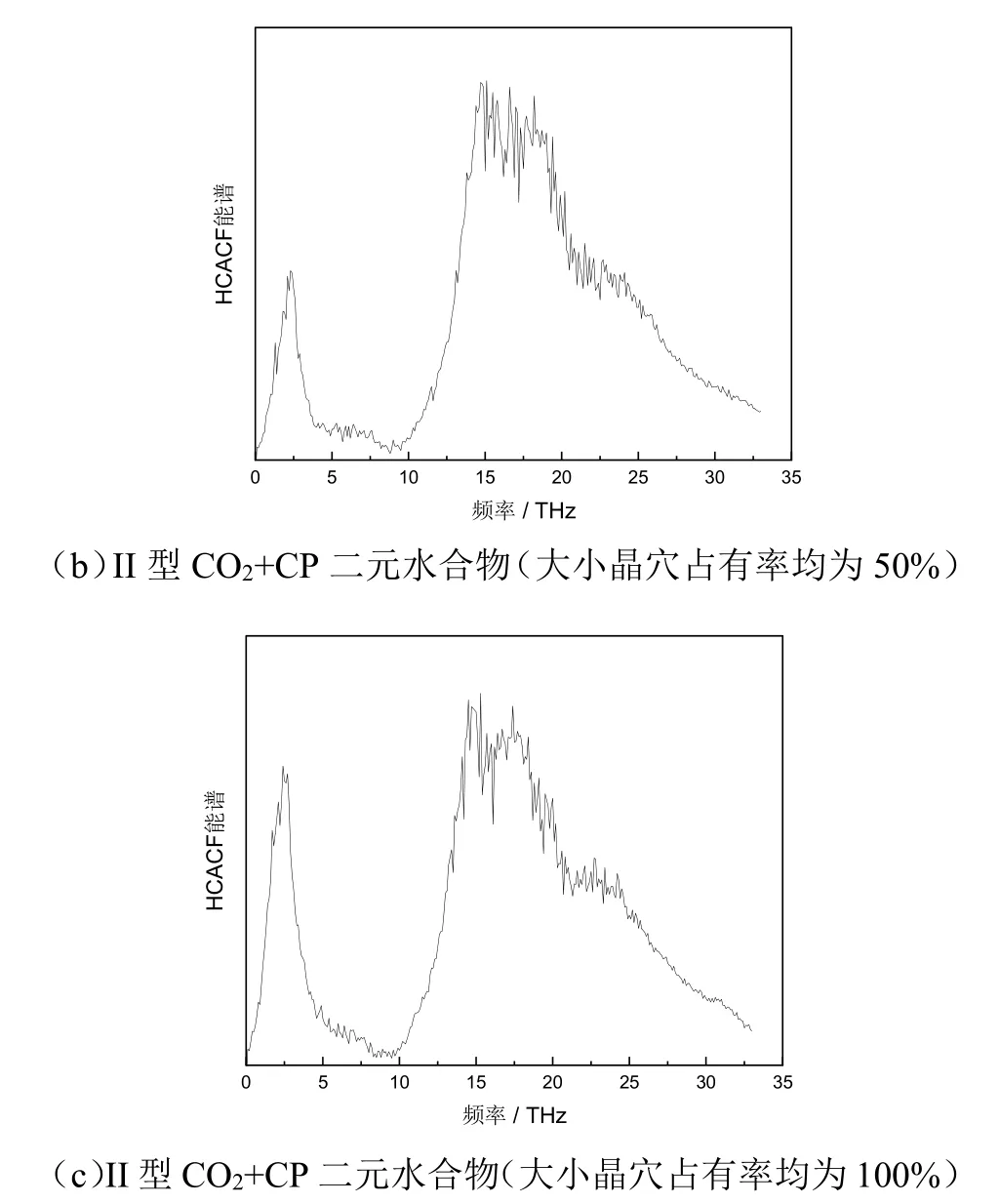
图6 二元水合物热流自相关函数能谱Fig.6 Power spectra of HCACF in CO2-CP hydrate

2.3 不同结构二氧化碳水合物的热物性

针对表1 列出的4 个不同体系，在50-200K温度范围内，计算了不同结构二氧化碳水合物的热物性，包括密度、等温压缩系数、声学速度、比热、热导率、热扩散率和声子平均自由程。表4 是不同结构二氧化碳水合物的密度，可以看出，当气体水合物结构一定时，温度越低，密度越大，这是由于温度越低，分子的势能越低，分子之间的相互作用力越大，水合物越稳定，此时分子热运动缓慢，客体分子位于晶穴中心，主客体分子间吸引力较大，因此体积较小，密度较大。相同温度下，不同结构气体水合物的密度排序为：I 型CO2水合物，II 型CO2+CP 二元水合物（综合晶穴占有率100%），II型CO2水合物（综合晶穴占有率66.7%）和II 型CO2+CP 二元水合物（综合晶穴占有率50%），可见晶穴占有率越高，客体分子对密度的贡献越大，密度越大。Chialvo 等[28]使用水分子SPC/E 模型计算的I 型CO2水合物在270K、5MPa 下的密度为1.181g/cm3，与200K、20MPa 条件下的模拟结果（1.189g/cm3）相接近，而且满足温度越低，密度越大的规律。不同结构不同温度二氧化碳水合物的等温压缩系数如表5所示，可以看出，相同结构的水合物，温度越低，等温压缩系数越低。Ning 等[29]在20MPa、271.15K 条件下模拟了I 型CO2水合物的等温压缩系数，约为1.1×10-4MPa-1，与表5 中20MPa、200K 条件下的模拟结果0.8753×10-4MPa-1在同一个数量级，而且满足温度越高，等温压缩系数越大的规律。

表4 不同结构二氧化碳水合物的密度（g/cm3）Table 4 Densities of carbon dioxide hydrates with different structures

表5 不同结构二氧化碳水合物的等温压缩系数（×10-4 MPa-1）Table 5 Isothermal compressibility of carbon dioxide hydrates with different structures

声学速度是影响固体热输运的重要参数，仅与密度和等温压缩系数有关，计算结果如表6所示。Jiang 等[26]在0.1MPa、150K 条件下通过分子动力学模拟得到的二氧化碳水合物的声学速度是3300m/s，与表6 所列20MPa、150K 条件下的声学速度3321.78m/s 相差不大。可以看出，温度越低，声学速度越高，而且I 型CO2水合物（晶穴占有率100%）的声学速度大于II 型CO2+CP 二元水合物（晶穴占有率100%），这是由于II 型水合物主客体分子之间耦合增强的缘故，当晶穴占有率降低时，主客体之间的耦合作用减弱（见图6），声学速度增大[30]。定容比热的计算结果如表7所示，可以看出，尽管水合物结构不同，但是随温度的变化趋势是一致的，温度越高，比容越大，这与Andersson 等[31]汇报的II 型四氢呋喃的比容以及黄文件等[32]汇报的天然气水合物的比容随温度的变化规律一致，而且相比于I 型水合物，II 型水合物的比热较小，而且随着晶穴占有率的下降而降低。因此，通过实验室合成的水合物或自然界中的水合物由于晶格结构缺陷，可能会存在比热低于理论值的情况。模拟得到的热扩散率如表8所示，对于I 型CO2水合物，大小介于2.83～6.40×10-7m2·s-1范围内，与姚贵策[25]测量的实验值（4～6×10-7m2·s-1）相差不大，而且可以看出，II 型水合物的热扩散率相对较大，尤其是晶格有缺陷的情况，热扩散率更大。声子平均自由程是由上述热物性参数根据公式求解得到的，计算结果如表9所示，可以看出，II 型二氧化碳水合物的声子平均自由程高于I 型二氧化碳水合物，这可能会影响到二者的分解行为，仍需要进一步研究。

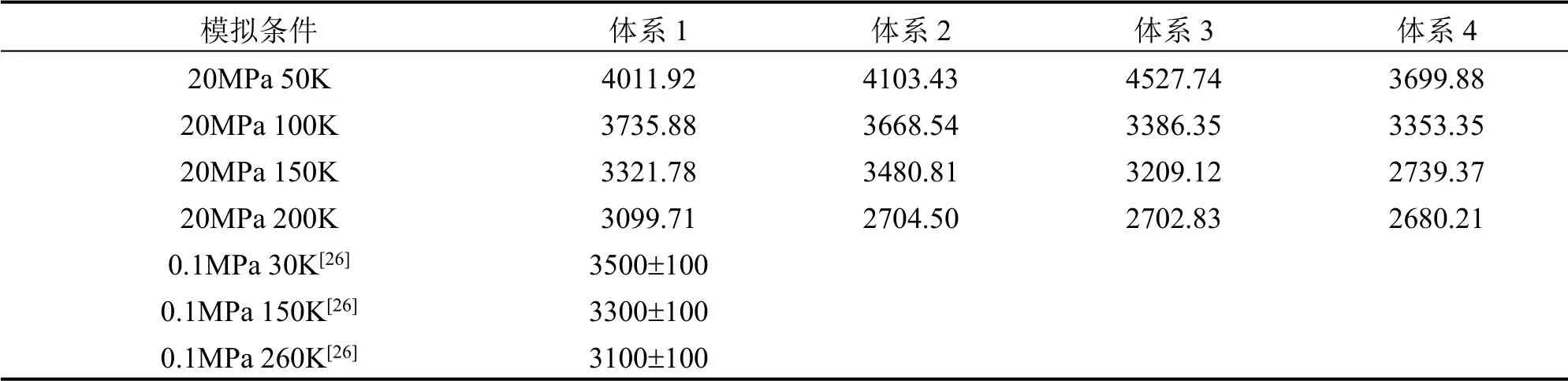
表6 不同结构二氧化碳水合物的声学速度（m/s）Table 6 Acoustic velocity of carbon dioxide hydrates with different structures

表7 不同结构二氧化碳水合物的比热容（kJ/kg·K）Table 7 Specific heat capacity of carbon dioxide hydrates with different structures

表8 不同结构二氧化碳水合物的热扩散率（×10-7 m2·s-1）Table 8 Thermal diffusivity of carbon dioxide hydrate with different structures

表9 不同结构二氧化碳水合物的声子平均自由程（Å）Table 9 Phonon mean free path of carbon dioxide hydrates with different structures

3 结论与展望

采用平衡分子动力学模拟手段，在20MPa、50-200K 条件下，测试了I 型CO2水合物、II 型CO2水合物（小晶穴占有率100%）、II 型CO2+CP二元水合物（大小晶穴占有率均为50%）和II 型CO2+CP 二元水合物（大小晶穴占有率均为100%）的热物性，包括密度、等温压缩系数、声学速度、比热、热导率、热扩散率和声子平均自由程。得到以下结论：（1）在环戊烷占据大晶穴条件下，II 型二氧化碳水合物的声子输运模式与I 型二氧化碳水合物不同，对于II 型水合物，随着大晶穴的晶穴占有率的增加，低频声子导热对水合物导热起到的作用也变得显著，高频声子和低频声子导热均对水合物导热起到重要作用。（2）当气体水合物结构一定时，温度越低，密度越大，等温压缩系数越低，声学速度越高，比热容越小。晶穴占有率均为100%时，与II 型二元水合物相比，在相同的温度和压力条件下，I 型CO2水合物密度更大，等温压缩系数更小，声学速度更大，比热容更大。密度和比热容均随着晶穴占有率的降低而降低。

II 型CO2水合物及多组晶穴占有率下II 型CO2+CP 二元水合物热物性的测试和导热机理的分析，为热力学促进剂环戊烷作用下二氧化碳水合物在空调蓄冷等领域的应用提供了基础数据，对于蓄冷量等参数的计算提供了依据。但是，本文对导热机理部分的研究尚不够深入。接下来，需要从声子输运的角度进一步研究不同结构下水合物的导热机理。另外，量子效应对分子动力学模拟的结果也需要进一步探讨。