热泵烘干机双蒸发器联合运行仿真
2022-03-22单惠敏李孔清
单惠敏 李孔清 李 荀
(湖南科技大学土木工程学院 湘潭 411100)
0 引言
闭式并联双蒸发器烘干机的蒸发器由于并联布置,可使其运行调节模式可多样化,能较好地适应不同物料的烘干需求,但在实践过程中由于运行工况的时变性,系统流态容易不稳定,需对其进行多次调节并测试,耗时耗力,制约了该项技术的推广。
现阶段有关于蒸发器的仿真研究[1-8]大多采用分区模型与分布参数模型相结合的方法,但均采用将蒸发器出口参数作为已知条件推出入口参数的方法。这需要对出口焓值进行假设,若假设值出现偏差,则仿真程序很难收敛。
本文采用分区分布参数模型方法,将蒸发器划分为若干微元段,以蒸发器微元段的入口参数作为已知条件,通过计算得出微元段的出口参数,经循环最终得到蒸发器的出口参数。先后开发单蒸发器和并联双蒸发器的仿真模型,并将其开发成软件。经多次模拟实验,证明该仿真程序具有很好的收敛性。本文蒸发器仿真程序中,制冷剂R134a 的物性参数均调用制冷剂物性计算软件REFPROP。
1 单蒸发器仿真
1.1 单蒸发器数学模型
本文将蒸发器简化为两相区与过热区[9],分别对两区域建立数学模型,并开发蒸发器仿真程序。在计算模块中,将蒸发器划分为若干微元,根据蒸发器内部及外部的传热分别对蒸发器建立数学模型。
将蒸发器入口参数作为已知参数,即第一个微元的入口参数,由仿真计算得到第一个微元的出口参数,将第一个微元的出口参数作为第二个微元的入口参数,以此循环最终得到蒸发器的出口参数。由于蒸发器入口制冷剂为近液体,初始进入蒸发器的制冷剂干度取0.3[10],当干度为1 时结束两相区模块,进入过热区模块。两区域计算方法主要区别为两相区需考虑蒸发器制冷剂侧压降。
1.1.1 过热区数学模型
由于过热区段一般距离较短,且过热区压降远小于两相区压降,对制冷剂温度的变化影响甚微,因此过热区的压降变化忽略不计。对蒸发器过热区建立数学模型如下。
蒸发器传热等式:
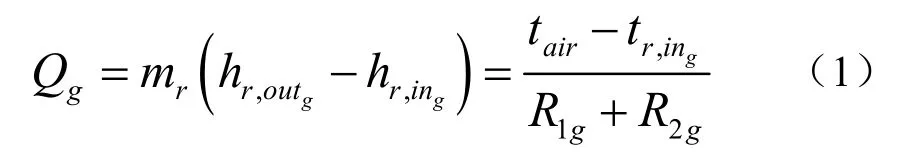
式中:Qg为过热区微元段制冷量,W;mr为制冷剂的质量流量,kg/s;分别为过热区微元段制冷剂的出口和入口焓值,J/kg;tair为蒸发器侧空气温度,K;为微元段制冷剂入口温度,K;R1g为过热区微元段制冷剂与管内壁的传热热阻,W/K;R2g为过热区微元段空气与管外传热面的传热热阻,W/K。
制冷剂与管内壁的传热热阻:

式中:hing为制冷剂与管内壁之间的对流换热系数W/(m2·K);A为蒸发器内微元段的有效换热面积,m2。
蒸发器内微元段的换热面积:

式中:dn为蒸发器管内径,m;lr为蒸发器微元段的长度,m。
制冷剂与管内壁之间的对流换热系数:

式中:Nu为代表制冷剂的努塞尔数;λ为制冷剂的导热系数,W/(m·K)。
1.1.2 两相区数学模型
制冷剂进入蒸发器时首先进入两相区,此时制冷剂为气液混合态,制冷剂的温度变化较大,压降不可以忽略不计。两相区较过热区增加了制冷剂侧的压降模型。且在两相区,蒸发器的换热性能是正常工况下的2.8-2.9 倍[11]。
制冷剂侧压降方程[12]:
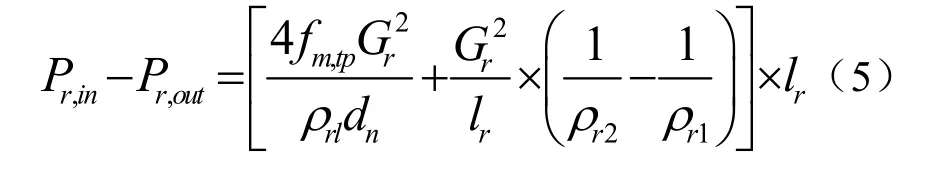
式中:Pr,in、Pr,out为两相区微元段内制冷剂进口、出口压力,Pa;fm,tp为两相区微元段内摩擦因子;Gr为制冷剂质量流速,kg/(m2·s);ρr1、ρr2为两相区微元段内制冷剂的入口、出口密度,kg/m3;ρrl为两相区微元段内液相制冷剂的密度,kg/m3。lr为蒸发器微元段的长度,m。
1.1.3 制冷剂内换热系数及无量纲数计算
由于制冷剂状态不同,两相区以及过热区中制冷剂与管内壁之间的对流换热系数的计算方式也有所不同。
过热区的对流换热系数计算采用的是Dittus-Boelter 关联式[13]:

其中在本文提出的蒸发器仿真模型中雷诺数与普朗特数的计算公式如下:

式中:ur为制冷剂流速,m/s;dn为蒸发器管内径,m/s;ν为制冷剂的运动粘度,m2/s;μ为制冷剂的动力粘度,kg/(m·s);Cp为制冷剂的定压比热容,J/(mol·K);λ为制冷剂的导热系数,W/m·K。
两相区对流换热系数关联式[14]:
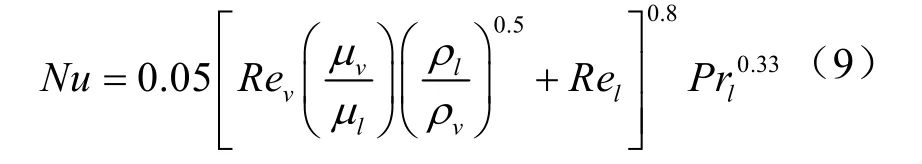
式中:μν、μl为制冷剂气相、液相状态下的动力粘度,kg/(m·s);ρν、ρl为制冷剂气相、液相状态下的密度,kg/m3。
雷诺数与普朗特数的计算公式与上述一致。
两相区内摩擦因子计算公式如下:

1.1.4 空气侧对流传热系数
若求空气与管外传热面之间的传热热阻,首先需要计算空气与管外传热面之间的对流换热系数。计算公式如下:
空气与管外传热面之间的传热热阻:

式中:A为蒸发器外侧微元段与空气接触的有效换热面积,m2;hout为空气与管外传热面之间的对流换热系数,W/(m2·K)。
蒸发器外侧与空气接触的有效换热面积:

式中:dw为蒸发器管外径,m;lr为蒸发器微元段的长度,m。
空气与管外传热面之间的对流换热系数:

式中:λ为空气导热系数,取0.0251W/(m2·K)。
本文选用的蒸发器物理模型为翅片管式蒸发器,翅片为铝制三角波纹型翅片。根据李妩等人通过实验拟合的换热关联式[15],努谢尔数Nu的计算公式采用三角波纹形翅片管式蒸发器的计算关联式。
三角波纹形翅片管式蒸发器:

上述关联式中雷诺数Re计算公式为:

其中,ωmax为最大迎面风速,计算公式为:
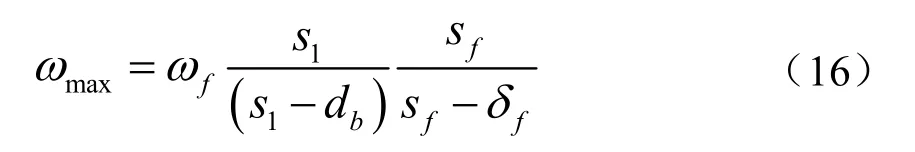
式中:sf为翅片间距;dw为蒸发器管外径,m;n为蒸发器中管排数量;s2为空气流动方向上的管间距,m;s1为迎风面管间距,m;db为考虑翅片厚度后的管外径,m;δf为翅片厚度,m;ν为空气的运动粘度。
1.2 系统原理图
图1 为烘干系统原理图,两个蒸发器所处工况不同,蒸发器A 置于烘干箱内风机环境中,蒸发器B 置于室外环境中,取空气干球温度为27℃,湿球温度为19℃。单蒸发器运行时蒸发器B 运行,蒸发器A 停止工作,此时为升温模式。双蒸发器运行时两个蒸发器同时工作,俩蒸发器处于并联状态,此时为升温和除湿模式。蒸发器A 所处环境的温度始终高于蒸发器B。
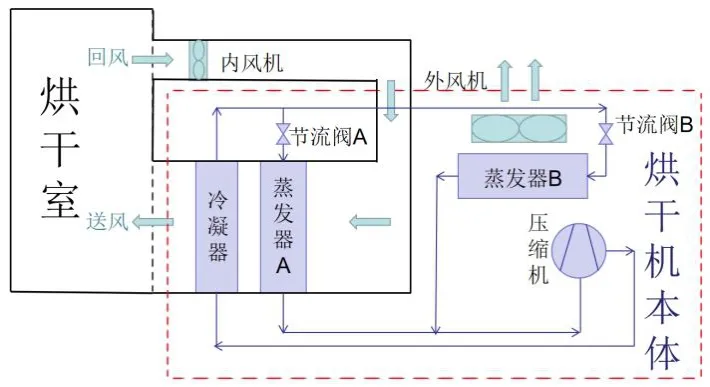
图1 烘干系统原理图Fig.1 Schematic diagram of drying system
1.3 单蒸发器仿真
建立蒸发器数学模型后,在Visual Studio C++环境下将数学模型进一步开发单蒸发器过热区与两相区的仿真程序。区域的算法流程如图2所示。整个蒸发器的仿真程序算法流程如图3所示。
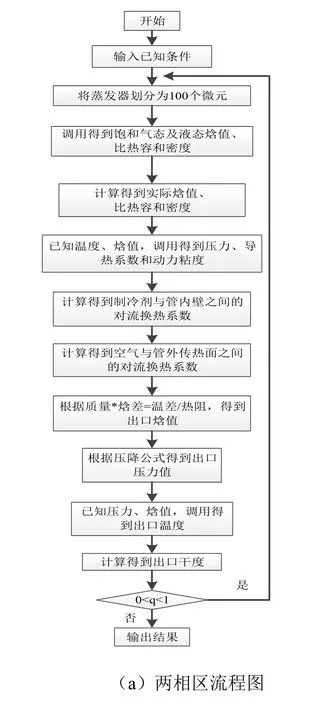
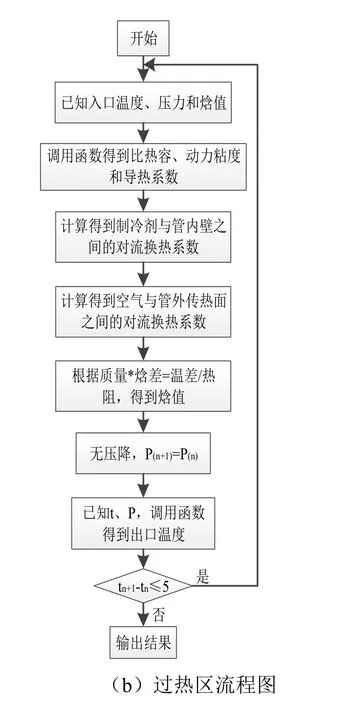
图2 两相区和过热区流程图Fig.2 Flow Chart of Two-phase Zone and Overheat Zone
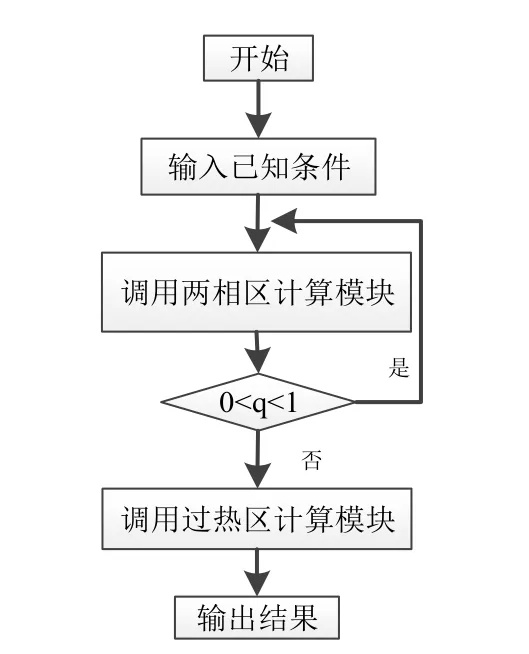
图3 蒸发器整体仿真流程图Fig.3 Flow chart of overall simulation of evaporator
2 双蒸发器联合运行仿真
2.1 并联双蒸发器流量校正算法
当两个蒸发器并联时,总体积流量G始终保持不变。仿真模型的关键在于如何分配两个蒸发器的制冷剂流量,使得蒸发器A 和蒸发器B 的压降最终始终保持相等。并联双蒸发器仿真程序的算法核心是蒸发器中制冷剂的流量校正算法。类比于流体力学中并联管路的计算原则和压强损失与流体流量的关系。
蒸发器A 与蒸发器B 压降与体积流量的关系:

式中:GA、GB为蒸发器A、蒸发器B 中制冷剂流量,m3/s;SA、SB为蒸发器A、蒸发器B 的阻抗;ΔPA、ΔPB为蒸发器A、蒸发器B 的压降,Pa。
流量校正算法如下:
(3)假设下一步迭代蒸发器A 的流量修正值为ΔG,在流量变化不大的情况下,可近似认为SA和SB和n保持不变,同时满足式(17)和(18),即:

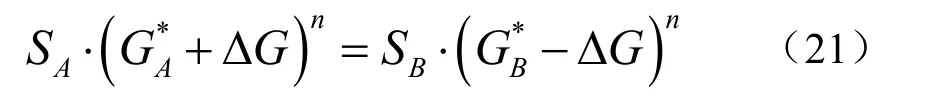
解得蒸发器A 的流量修正值ΔG为:
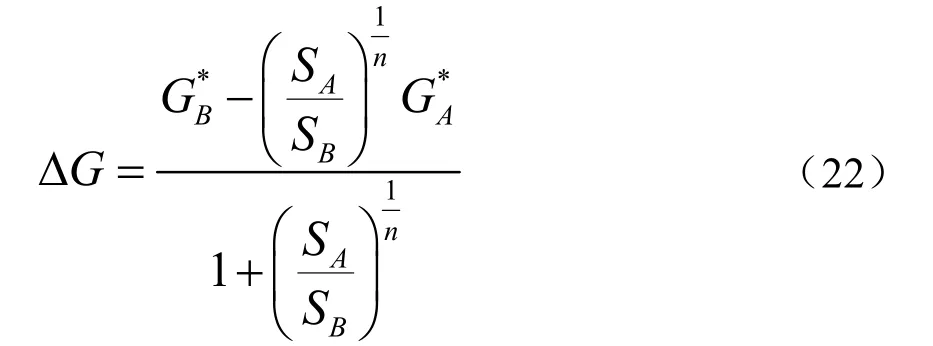
在水路中n的取值范围为1~2 之间,本文通过单蒸发器仿真程序,基于多组体积流量G和压降ΔP,对函数进行拟合。制冷剂压降与流量关系的拟合线与仿真计算对比结果见图4。当n=2.5 时,拟合相关度R2=0.99885,拟合效果好。此时S=7.64×1014。得到蒸发器中制冷剂压降的估算方法,即ΔP=S·G2.5。

图4 拟合曲线与仿真结果对比Fig.4 Compare with fitting curve and simulation data
2.2 并联双蒸发器仿真程序算法
以单蒸发器数学仿真模型为基础,通过流量校正算法来保证并联双蒸发器的压降始终保持相等。利用Visual Studio C++将并联蒸发器计算模型开发成仿真程序,其仿真程序算法流程如图5所示。
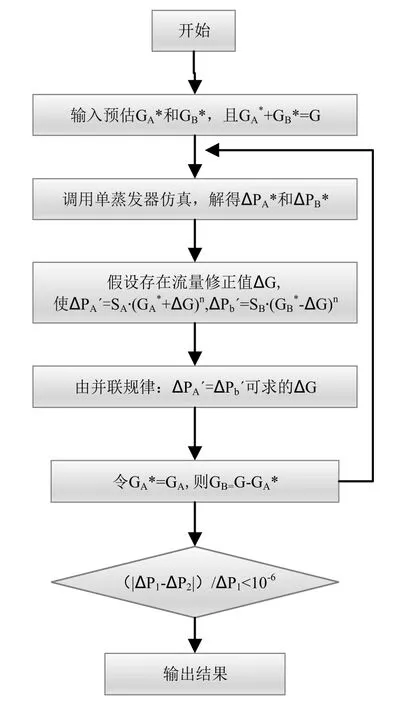
图5 并联蒸发器流程图Fig.5 Flow chart of parallel evaporator
3 研究结果与验证
3.1 研究结果
根据数学模型及仿真算法,将程序开发成软件,软件界面如图所示,其中图6 为蒸发器结构参数输入模块,可分别输入两个并联蒸发器的结构参数。图7 为并联双蒸发器软件计算界面,输入制冷剂参数与空气进口参数,点击“开始仿真”按钮,即可对整个并联双蒸发器程序进行仿真,并输出结果。
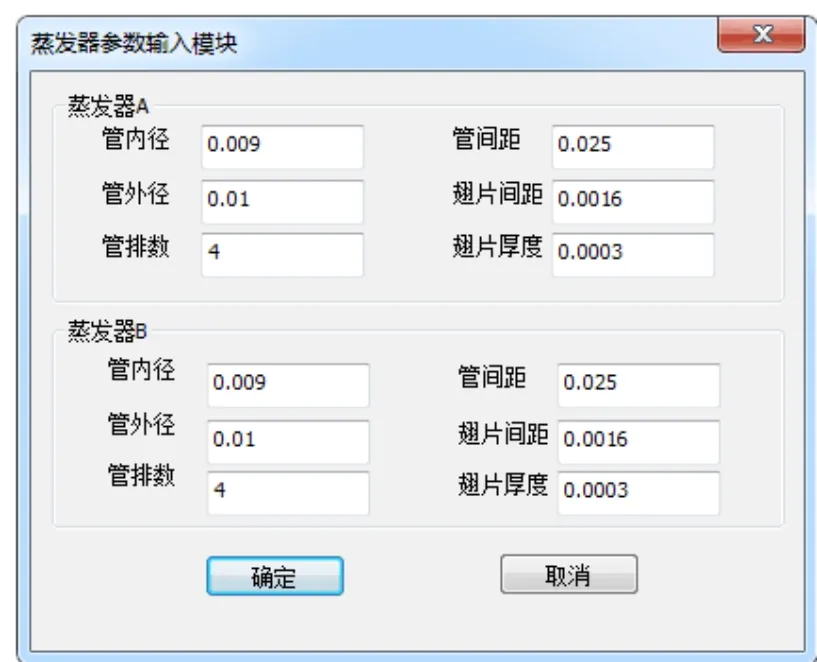
图6 蒸发器结构参数输入模块Fig.6 Evaporator structural parameter input module
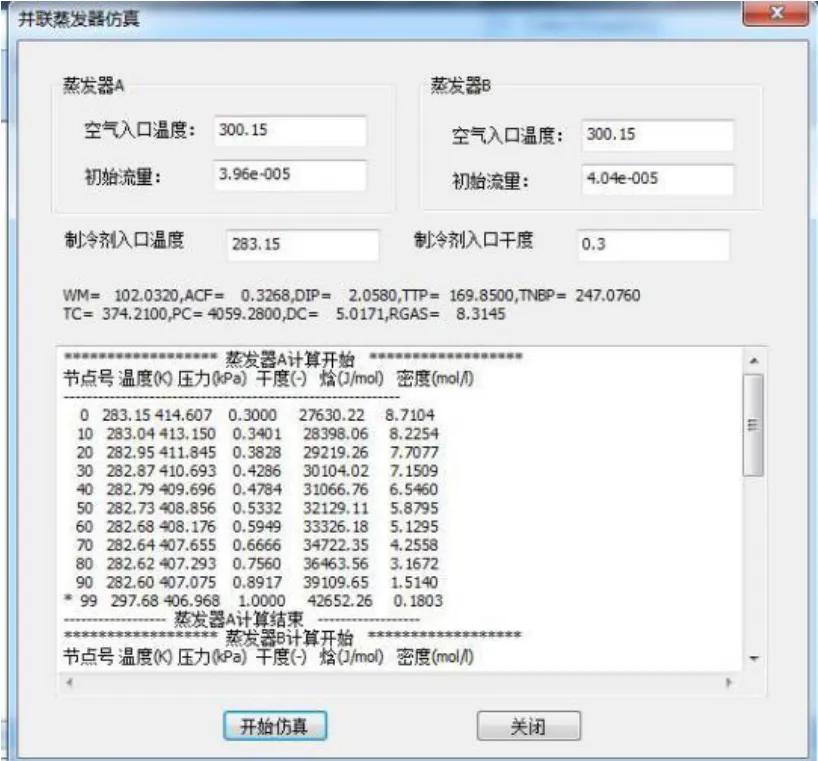
图7 并联双蒸发器软计算界面Fig.7 Parallel double evaporator software calculation interface
3.2 流量修正算法验证
通过蒸发器制冷剂流量的校正算法验证来判断双蒸发器联合运行仿真程序的可行性。流量校正算法进行验证时,两个蒸发器的结构需保持一致。将两个蒸发器流量设置为不同值,流量校正100次,通过并联双蒸发器程序对流量重新进行分配,最终得到的流量分配结果及误差如表1所示。

表1 流量校正前后蒸发器体积流量及压降Table 1 Volume flow and pressure drop of evaporator before and after flow correction
由上述运行结果发现,并联的两个蒸发器结构参数以及制冷剂空气参数相同时,无论最初两个蒸发器的流量取何值,在经过流量分配后,并联的两个蒸发器流量及压降都趋于一致。证明本文提出的并联双蒸发器联合运行仿真程序在理论的可行性与流量修正算法的可靠性。
4 结论
(1)提出一种新的单蒸发器仿真算法,采用分布参数模型,将蒸发器划分为若干个微元段,成功实现由蒸发器入口参数得到蒸发器出口参数,克服了以往蒸发器模拟中假设出口压力为基础算法的缺点。
(2)以单蒸发器仿真算法为基础,根据并联蒸发器压降始终相等的原则,提出了一种新的流量校正算法计算并联双蒸发器流量。
(3)在Visual Studio C++环境下建立并联双蒸发器联合运行仿真模型且具有很好的收敛性,并将其开发成软件,经验证,其软件模型具有很好的可靠性,在工程上有一定的指导意义。
