对一道多项式问题的解析

2022-03-21刘合国徐行忠

大学数学 2022年1期

刘合国，徐行忠，廖军

(湖北大学数学与统计学学院，武汉430062)

1 引言

多项式是高等代数的重要内容之一，多项式的整除性是多项式的非常基本的性质.本文将讨论李炯生、查建国、王新茂编著的《线性代数》习题1.3.10，见[1，习题1.3.10]，并给出其解析.通过对这道多项式问题的解析来阐述处理多项式这类问题的方法和技巧.笔者认为题目中应该有一个打印错误，即所求多项式的次数应该是2n-1，以确保解的唯一性.事实上，如果f(x)是满足题目条件的多项式，设f(x)=q(x)(x2-1)n+r(x)，其中r(x)为余式，则r(x)也是满足条件的多项式.解法1运用了中国剩余定理，见[2，第三章，定理6]，从中国剩余定理的角度能更清楚地看到该问题的本质.在此解答过程中利用二项式展开定理将1表示为两个多项式的组合改写成它们方幂的组合，此技巧可应用于中国剩余定理求解的关键一步.利用此技巧也可方便地求解[1，例1.3.3].在多项式互素的情形下提供了除辗转相除法和待定系数法之外的一种方法.

2 预备和问题

本文采用的术语和符号都是标准的，按照[1，3].

首先，回顾一下多项式的中国剩余定理.设F[x]为域F上一元多项式环，设f(x)，g(x)，p(x)∈F[x].如果p(x)整除f(x)-g(x)，则称f(x)与g(x)模p(x)同余，记作f(x)≡g(x)(modp(x)).多项式的中国剩余定理可表述为:

设pi(x)为n个两两互素的多项式，对于任意n个多项式ri(x)，同余方程组

f(x)=ri(x)(modpi(x))， 1≤i≤n.

下面只说明n=2的情形.

定理1(多项式的中国剩余定理)设p1(x)，p2(x)是F[x]的两个互素的多项式，则对任意多项式r1(x)，r2(x)，存在唯一次数小于p1(x)p2(x)次数的多项式f(x)使

证由于(p1(x)，p2(x))=1，则存在多项式u(x)，v(x)，使得u(x)p1(x)+v(x)p2(x)=1.取

f1(x)=v(x)p2(x)，f2(x)=u(x)p1(x)，

则

fi(x)≡δij(modpj(x))，

其中δij为Kronecker符号，1≤i，j≤2.记

f(x)=r1(x)f1(x)+r2(x)f2(x)=q(x)p1(x)p2(x)+r(x)，

则r(x)即为所求同余方程组的解.

下证解的唯一性.设f(x)，g(x)都是满足定理中同余方程组的解，即

f(x)≡ri(x)(modpi(x))， 1≤i≤2，

g(x)≡ri(x)(modpi(x))， 1≤i≤2.

则f(x)≡g(x)(modpi(x))， 1≤i≤2.所以

f(x)≡g(x)(modp1(x)p2(x)).

从而f(x)=g(x).

接下来证明一个引理.此引理可应用于多项式环上的中国剩余定理求解中的关键一步.

引理1如果k(x)p(x)+l(x)q(x)=1，设

则u(x)pm(x)+v(x)qn(x)=1.特别地，(pm(x)，qn(x))=1.

证利用二项式展开定理

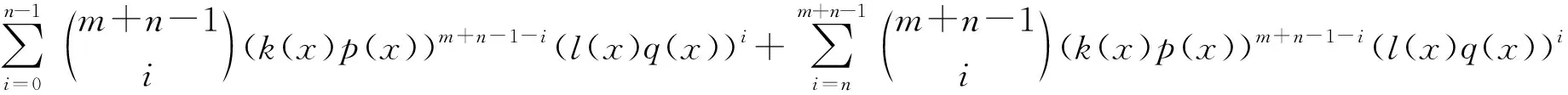
=pm(x)u(x)+qn(x)v(x).

利用上述引理1容易计算出[1，例1.3.3]中的u(x)，v(x)使得

xmu(x)+(1-x)nv(x)=1.

由于x+(1-x)=1，则

即为所求，其中u(x)的次数小于n，v(x)的次数小于m.

此方法同样适用于[1，习题1.3.6(1)(2)].

3 问题解析

习题1([1，习题1.3.10]) 设f(x)是数域F上次数为2n-1的多项式，且

(x-1)n|f(x)+1，(x+1)n|f(x)-1.

求f(x).

解法1运用中国剩余定理.

习题1等价于求下列同余方程组在模(x2-1)n下的解.

由于(x-1)n与(x+1)n互素，根据多项式的中国剩余定理，同余方程组在模(x2-1)n意义下有唯一解.

因为((x-1)n，(x+1)n)=1，那么存在次数小于n的多项式u(x)，v(x)∈F[x]，使得

u(x)(x-1)n+v(x)(x+1)n=1.

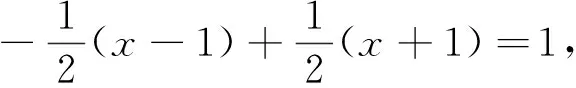
则u(x)(x-1)n+v(x)(x+1)n=1.令

f(x)=u(x)(x-1)n-v(x)(x+1)n，

则有(x-1)n|f(x)+1，(x+1)n|f(x)-1且f(x)的次数为2n-1.所以

即为所求.

注意到

1=u(x)(x-1)n+v(x)(x+1)n，f(x)=u(x)(x-1)n-v(x)(x+1)n.

则有

f(x)=2u(x)(x-1)n-1=1-2v(x)(x+1)n，

即

或者

记mjk=min{n-1，2n-1-j+k}，mk=max{n，k}，ljk=2n-1-j+k.则

一般地，上述方法可以用于求次数为m+n-1的多项式f(x)，使得(x-1)m|f(x)+1，并且(x+1)n|f(x)-1.此时令

则

f(x)=u(x)(x-1)m-v(x)(x+1)n

即为所求.

此方法同样适用于求解[1，习题1.3.8].

解法2利用Taylor展开式.

注意到(x-1)n|f(x)+1当且仅当f(1)=-1，f′(1)=f″(1)=…=f(n-1)(1)=0.同样地，(x+1)n|f(x)-1当且仅当f(-1)=1，f′(-1)=…=f(n-1)(-1)=0.

因为(x-1)n|f(x)+1，由Taylor展开式，不妨设

又(x+1)n|f(x)-1当且仅当x+1|f(x)-1且(x+1)n-1|f′(x).由f(-1)=1知2=(-2)na0，从而a0=(-1)n21-n.

为方便，这里设an=0.令

其中an=0.则f′(x)=(x-1)n-1g(x).因此(x+1)n-1|f′(x)当且仅当(x+1)n-1|g(x)当且仅当(n+i)ai-2(i+1)ai+1=0.对任意的0≤i≤n-2成立.由(n+i)ai-2(i+1)ai+1=0可得递推关系式

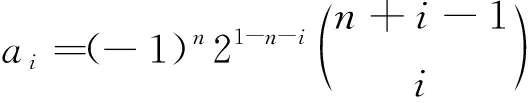
即为所求的多项式.

为了考虑x0为多项式g(x)的根及其重数问题，可将g(x)在x0处按Taylor展开，即

其中m为g(x)的次数.则(x-x0)k|g(x)当且仅当g(i)(x0)=0，i=0，1，…，k-1.

上述方法同样适用于求次数为m+n-1的多项式f(x)，使得(x-1)m|f(x)+1，并且(x+1)n|f(x)-1.此时

解法3解方程组.

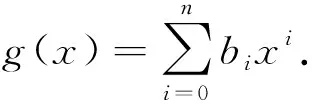
gk+1(x)=ngk(x)-xg′k(x)，

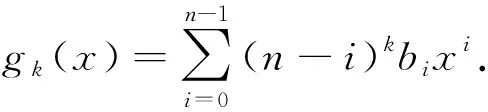
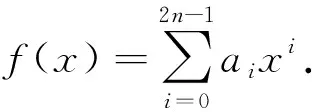
对1≤k≤n-1，有

分别求上述方程的和与差，有

因此

上述方法在理论上可适用于求次数为m+n-1的多项式f(x)，使得(x-1)m|f(x)+1，且(x+1)n|f(x)-1.但是当m≠n时关于系数的方程并不易求出其具体的解.

解法4运用积分方法求解.

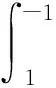
又

即为所求，即

[1，习题1.3.10]出现了三个具有相同导函数的多项式，即f(x)和f(x)±1.根据此特点，先求出含待定系数的导函数f′(x)，再积分求得含待定系数的原函数f(x)，通过f(x)±1的根来确定系数，并最终得到f(x).

上述方法同样适用于求次数为m+n-1的多项式f(x)，使得(x-1)m|f(x)+1，并且(x+1)n|f(x)-1.此时

比较上述四种解法，解法1更具有一般性并且能够深入问题的本质.首先借助多项式的中国剩余定理可以明确解的存在唯一性，并利用定理可以给出具体的解.一方面，解法2、解法3和解法4局限于一次不可约因式情形，特别是解法3在m=n时才最有效，而解法1对于一般的互素因式方幂仍然适用.另一方面，在利用这些方法求解之前，尤其是解法2和解法3采用的待定系数法是需要解在存在假设下的形式即解的次数条件.而习题中解的次数条件可以利用中国剩余定理来确定，在此前提下才使得使用待定系数法成为可能.同时还可以利用中国剩余定理得到解的存在唯一性.因此在这种意义下，从中国剩余定理的角度可以更清楚地看到该问题的本质.当然，正如前言中所提到的，解的次数条件也可以通过带余除法得到.解的唯一性可以通过同余性质来证明，即多项式中国剩余定理证明过程中解的唯一性部分.但是存在性却需要通过求解待定的系数方程是否有解得出.特别是解法3在m≠n时对应的方程并不容易求解.在已经知道解的存在唯一性前提下，可以得到解法3中m≠n时待定系数方程解的存在唯一性，从而得到对应的系数矩阵可逆.读者也可尝试给出系数矩阵可逆的一个直接的证明.

值得一提的是，通过不同的解法可以得到一些有趣的组合恒等式.例如由解法1和解法2的解

可以得到

由解法1和解法4的解

得到

有兴趣的读者还可以利用上述不同解法得到的解的不同表达式来推导出其他形式的组合恒等式.