量子仿射李超代数Uq(osp(2n+1|2m)(1))的Serre关系
2022-03-21王明豪
王明豪, 许 莹
(合肥工业大学 数学学院,合肥230601)
1 引 言
李超代数作为一类重要的超代数在各个领域均有发展和应用.20世纪40年代,李超代数作为一个重要的例子出现在代数几何的研究过程中.之后,Gerstenhaber在探讨环与代数的形变理论的一系列工作中也发现了李超代数[1].与此同时,李超代数在Spencer研究流形的pseudogroup结构中也发挥了重要的作用[2].从20世纪70年代开始,物理学家把李超群(李超代数)应用到量子场论的超对称性的研究中,从而将具有不同自旋和统计性质的粒子联系起来,建立了一系列的超对称理论模型并得到了相应的实验证实.1977年,Kac首先给出了有限维单李超代数的分类[3],从而奠定了之后很多李超代数和李超群研究工作的基础.
量子超代数作为李超代数的量子形变代数也日益引起关注.1988年,Kulish引入了量子超群Uq(osp(2|1))的结构.不久,Tolstoy[4]定义了所有的Kac-Moody超代数的量子超代数,并给出了q-形变的Cartan-Weyl基以及extremal projectors的具体表达式.量子超代数最重要的性质是具有Hopf超代数结构及辫子结构,这使得它迅速在范畴论[5-7]和表示论[8]中产生巨大影响.
Serre在研究有限维李超代数的结构中给出了有限维半单李代数的Chevalley生成元和Serre关系的表达式,从而给出了李代数最常用的实现形式.这些表达式在李代数的表示论中起了非常重要的作用.之后,Gabber和Kac将这些结论推广至Kac-Moody代数[9].这些表达式已经成为李代数的经典结构表达式.但由于李超代数结构的复杂性,长时间以来,李超代数的Serre关系式一直不够清晰.张瑞斌教授在研究李超代数的量子泛包络代数的过程中给出了李超代数的Serre表达式[10].张瑞斌教授在论文中指出,在李超代数的结构中,不仅存在Serre关系,还存在更深层次的关系,被称为高阶Serre关系.这些研究成果在量子超代数中起到非常重要的作用,特别是在低微拓扑[11],统计物理[12],非交换几何[13]等领域.
论文将在参考文献[10]的研究基础之上,延续Kac在参考文献[3]中采用的记号,对李超代数osp(2n+1|2m)(1)的所有根系情况展开讨论,给出Uq(osp(2n+1|2m)(1))的Serre关系的具体表达形式(参见定理1).
2 量子仿射李超代数osp(2n+1|2m)(1)
下面,将给出论文需要的基础理论知识.
2.1 李超代数的定义
首先,回顾李超代数的定义.
定义1(李超代数的定义) 李超代数是超代数G=G0⊕G1具有一个算子[,],且满足以下公理:
[a,b]=(-1)(dega)(degb)[b,a], [a,[b,c]]=[[a,b],c]+(-1)(dega)(degb)[b,[a,c]].
用元素εi来表示李超代数根系的偶部,用元素δv来表示李超代数根系的奇部.给定正整数k和l,令ζ(k|l)是上由元素εi(i=1,2,…,k)和δv(v=1,2,…,l)组成的k+l维向量空间.赋予ζ(k|l)一个对称的非退化双线性形式(见[1]).设g是一个特殊的线性或正交辛李超代数.选择尽可能最小的正整数k和l.则g的根系集Φ可以表示成ζ(k|l)的子集.
为了描述仿射李超代数osp(2n+1|2m)(1)的根系,在向量空间ζ(k|l)原有的基元素中增加一个新的元素ε0=δ,将新的向量空间记为εδ(k|l).并通过下式将ζ(k|l)的双线性型扩充为εδ(k|l)的双线性型{见[12]).则osp(2n+1|2m)(1)的根系可表示为
αi=εi-εi+1(1≤i 注 对于仿射李超代数osp(2n+1|2m)(1)来说,这里的元素ε0=δ属于偶部. 定义2对所有的i,j,定义bij=(αi,αj).则李超代数g对应于根系Π的Cartan矩阵可表示为A=(aij),其中 注1αii=0当且仅当αi是一个奇的迷向根. 根据Kac在参考文章[3]的讨论,可以用邓肯图[3]来表示李超代数的根系.用表示偶根,用⊗表示奇的迷向根,用⊕表示奇的非迷向根,用×表示或⊗,具体取决于根是奇的还是偶的. 注2 (i) 这里的符号与参考文献[3]略有不同; 定义3李超代数osp(2n+1|2m)(1)所有可能的邓肯图如下表所示: 类型g=osp(2n+1|2m)(1)类型g=osp(2n+1|2m)(1)(1)·○⇒·○×…×⇒·○α0α1 αm+n·○⇒·○×…×⇒α0α1 αm+n(3)×·○α0·○α1 αm+n…×⇒·○×·○α0·○α1 αm+n…×⇒(2)·○⇒·○2←…→×α0 α1 αm+n·○2←…→×⇒α0 α1 αm+n(4)×α0α1 αm+n…×⇒·○×α0α1 αm+n…×⇒ 量子仿射李超代数是论文的研究对象,下面介绍量子仿射李超代数的定义. 定义4设Uq(g,Π)是上对应于李超代数g的基础根系Π的量子化泛包洛超代数[3],其生成元为ei,fi,ki±1,其中es,fs,(s∈τ)是奇元素,其余的元素是偶元素.Uq(g,Π)满足以下关系式: (ii) 若ass=0,(es)2=(fs)2=0, 若aii≠0,i≠j,(Adei)1-aij(ej)=(Adfi)1-aij(fj)=0, (iii) 与邓肯图相关的高阶Serre关系如下: (其中图Ⅰ,图Ⅱ,图Ⅲ中的⊗均表示第s个位置的根)相关的高阶Serre关系如下: AdesAdes-1Ades(es+1)=0,AdfsAdfs-1Adfs(fs+1)=0, [Ades+1(es),[Ades+1(es),Ades(es-1)]v1]v2=0, 其中v1=q-(αs,αs+1),v2=q(αs,αs+1); [Ades+2(Ades+1es),[Ades+1es,Adeses-1]v1]=0, 其中[a,b]v1=ab-v1ba. AdesAdes+1(es-1)-Ades+1Ades(es-1)=0, 注1q∈,且q≠0,±1.其中 下面,将给出量子仿射李超代数Uq(osp(2n+1|2m)(1))的Serre关系的具体表达式. 性质1① 若αi是偶根,则对所有的i≠j, ② 若αs是奇根且ass=2,且αj也是奇根.则对所有的j≠s, ③ 若αs是奇根且ass=2,且αj是偶根,则对所有的j≠s, 证分情况讨论:(i)当i∈τ,j∈τ时, (a) 若i=m+n,j=m+n-1,则(αi,αi)=-1,(αi,αj)=1且aij=-2.通过计算有 同理若i=0,j=1,可得到相同的等式. (b) 若i=m+n,j≠m+n-1,则(αi,αi)=-1,(αi,αj)=0且aij=0.通过计算有 同理若i=0,j≠1,亦可得相同等式. (ii) 当i∈τ,j∉τ时, (a) 若i=m+n,j=m+n-1,则(αi,αi)=-1, (αi,αj)=1且aij=-2.通过计算有 同理若i=0,j=1,可得到相同的等式. (b) 若i=m+n,j≠m+n-1,则(αi,αi)=-1,(αi,αj)=0且aij=0.通过计算有 同理若i=0,j≠1,亦可得相同等式. (iii) 当i∉τ,j∈τ时, (a) 若i=m+n,j=m+n-1,则(αi,αi)=1,(αi,αj)=-1且aij=-2.通过计算有 同理若i=0,j=1,可得到相同的等式. (b) 若i=m+n,j≠m+n-1,则(αi,αi)=1,(αi,αj)=0且aij=0.通过计算有 同理若i=0,j=1,可得到相同的等式. (c) 若1≤i≤m+n,j=i-1/i+1,此时需对αi进行讨论:若αi=εs-εs+1(1≤s≤i),则(αi,αi)=2,(αi,αj)=-1且aij=-1,通过计算有 Adei(ej)=eiej-q-1ejei, 若αi=δs-δs+1(1≤s≤i),则(αi,αi)=-2,(αi,αj)=1且aij=1,通过计算有 Adei(ej)=eiej-qejei, (d) 若1≤i≤m+n,j≠i-1/i+1,有(αi,αj)=0且aij=0.则通过计算有 类似(iii)亦可证i∉τ,j∉τ时的情形. 注意到以上均是关于元素ei部分的证明,仿照ei部分的证明可证明关于fi部分的等式亦成立. 根据上面的讨论,知道仿射李超代数Uq(osp(2n+1|2m)(1))具有不同的邓肯图. 一般情况下,不同的邓肯图对应着不同构的量子群结构.将按照邓肯图的不同,对高阶Serre关系分别展开论证. 为了书写的简便,引入如下的记号: 下面将分别给出高阶Serre关系的具体表达形式. 性质2图Ⅰ中的高阶Serre关系为 eses-1;s;s+1+(-1)[es-1][es+1]es-1;s;s+1es=0, fsfs-1;s;s+1+(-1)[fs-1][fs+1]fs-1;s;s+1fs=0. 证(i) 若αs=δt-εi(1≤t≤s,1≤i≤s),则通过邓肯图分析有 (a) 若s+1∈τ,则(αs,αs+1)=-1.此时有s-1∈τ,且(αs-1,αs)=1.则 Ades(es+1)=eses+1+q-1es+1es, Ades-1(Ades(es+1))=es-1eses+1+q-1es-1es+1es-qeses+1es-1-es+1eses-1, (b) 若s+1∉τ,则(αs,αs+1)=-1.此时有s-1∈τ,且(αs-1,αs)=1.则 Ades(es+1)=eses+1+q-1es+1es, Ades-1(Ades(es+1))=es-1eses+1-q-1es-1es+1es+qeses+1es-1-es+1eses-1, (ii) 若αs=εt-δt(1≤t≤s,1≤i≤s),则通过邓肯图分析有 (a) 若s+1∈τ,则(αs,αs+1)=1.此时若s-1∈τ,且(αs-1,αs)=-1.则 Ades(es+1)=eses+1+qes+1es, Ades-1(Ades(es+1))=es-1eses+1+qes-1es+1es-q-1eses+1es-1-es+1eses-1, (b) 若s+1∈τ,则(αs,αs+1)=1.此时若s-1∉τ,且(αs-1,αs)=-1.则 Ades(es+1)=eses+1+qes+1es, Ades-1(Ades(es+1))=es-1eses+1+qes-1es+1es-q-1eses+1es-1-es+1eses-1, (c) 若s+1∉τ,则(αs,αs+1)=1.此时若s-1∈τ,且(αs-1,αs)=-1,则 Ades(es+1)=eses+1-qes+1es, Ades-1(Ades(es+1))=es-1eses+1-qes-1es+1es+q-1eses+1es-1-es+1eses-1, (d) 若s+1∉τ,则(αs,αs+1)=1.此时若s-1∉τ,且(αs-1,αs)=-1.则 Ades(es+1)=eses+1-qes+1es, Ades-1(Ades(es+1))=es-1eses+1-qes-1es+1es-q-1eses+1es-1+es+1eses-1, 注意到以上均是关于元素ei部分的证明,仿照ei部分的证明我们可证明关于fi部分的等式亦成立. 仿照性质2的证明同样可以推出图Ⅱ以及图Ⅲ的高阶Serre关系等价表达式. 性质3图Ⅱ的高阶Serre关系为 eses-1;s;s+1+(-1)[es-1]es-1;s;s+1es=0,fsfs-1;s;s+1+(-1)[fs-1]fs-1;s;s+1fs=0. 性质4图Ⅲ的高阶Serre关系为 eses-1;s;s+1-(-1)[es-1]es-1;s;s+1es=0,fsfs-1;s;s+1-(-1)[fs-1]fs-1;s;s+1fs=0. 性质5(B)中的高阶Serre关系为 (es+1es+q-1eses+1)Es-1;s;s+1-v2Es-1;s;s+1(es+1es+q-1eses+1)=0, (fs+1fs+q-1fsfs+1)Fs-1;s;s+1-v2Fs-1;s;s+1(fs+1fs+q-1fsfs+1)=0. 其中 v2=q(αs,αs+1). 证Ades+1(es)=es+1es+q-1eses+1, [Ades+1(es),Ades(es-1)]v1=Ades+1(es)Ades(es-1)-v1Ades(es-1)Ades+1(es) [Ades+1(es),[Ades+1(es),Ades(es-1)]v1]v2 +q3es+1eses-1eses+1es-q3eses+1eses-1eses+1 =(es+1es+q-1eses+1)Es-1;s;s+1-v2Es-1;s;s+1(es+1es+q-1eses+1)=0. 仿照ei部分的证明可证明关于fi部分的等式亦成立. 性质6(C)中的高阶Serre关系为 e′s+2;s+1;sE′s;s-1;s+1-E′s;s-1;s+1e′s+2;s+1;s=0, f′s+2;s+1;sF′s;s-1;s+1-F′s;s-1;s+1f′s+2;s+1;s=0. E′s;s-1;s+1=(es+1;s;s;s-1+es;s-1;s+1;s-q2(es+1;s;s-1;s-es-1;s;s;s+1)+q(es;s+1;s-1;s-es;s-1;s+1;s) -q-1es;s+1;s;s-1+q3es-1;s;s+1;s], F′s;s-1;s+1=(fs+1;s;s;s-1+fs;s-1;s+1;s-q2(fs+1;s;s-1;s-fs-1;s;s;s+1)+q(fs;s+1;s-1;s-fs;s-1;s+1;s) -q-1fs;s+1;s;s-1+q3fs-1;s;s+1;s]. eg;h;uv=egeheuev,fg;h;uv=fgfhfufv. 证若s+2∈τ则 Ades+2(Ades+1es)=es+2es+1es-q-1es+2eses+1+q-1es+1eses+2-q-2eses+1es+2, [Ades+2(Ades+1es),[Ades+1es,Adeses-1]v1] -eses-1eses+1es+2es+1es+eses+1es-1eses+2eses+1-eses-1es+1eses+2eses+1-eses+1es-1eses+1eses+2 -es+1eses+2eses-1eses+1+eses+1es+2eses+1es-1es-eses+1es+2eses-1es+1es-eses+1eses-1es+2es+1es +eses+1es+2es+1eses-1es-eses+1es+2es-1eses+1es-eses+1es-1eses+2es+1es+eses-1es+1eses+2es+1es -es+1eses+2eses+1eses-1-eses+1es+2eses-1eses+1-eses+1eses-1es+2eses+1+eses+1eses-1es+1eses+2 +eses-1eses+1eses+1es+2)+q-3(eses+1es+2eses+1eses-1-eses+1eses-1eses+1es+2) =e′s+2;s+1;sE′s;s-1;s+1-E′s;s-1;s+1e′s+2;s+1;s=0. 同理可以证明s+2∉τ时的情形.仿照ei部分的证明可以得到fi所满足的等式. 性质7(D)中相关的高阶Serre关系为 e″s;s+1;s-1-e″s+1;s;s-1=0,f″s;s+1;s-1-f″s+1;s;s-1=0. 注意这里记号与上面略有不同,其中 证若s+1∈τ, Ades+1(es-1)=es+1es-1+q-1es-1es+1, AdesAdes+1(es-1)=es+1eses-1+q-1eses-1es+1-qes+1es-1es-es-1es+1es, Ades(es-1)=eses-1+q2es-1es, Ades+1Ades(es-1)=es+1eses-1+q2es+1es-1es-q-2es-1eses+1-es-1eses+1, AdesAdes+1(es-1)-Ades+1Ades(es-1)=es;s+1;s-1-es+1;s;s-1=0. 类似地,可以证明s+1∉τ时的情形.仿照ei部分的证明可以得到fi所满足的等式. 综上,总结出如下主要定理: 定理1设Uq(osp(2n+1|2m)(1))是上的量子化泛包洛超代数[3],其生成元为其中es,fs(s∈τ)是奇元素,其余的元素是偶元素.Uq(osp(2n+1|2m)(1))满足以下关系式 和如下的Serre关系式: ① 若αi是偶根,则对所有的i≠j, ② 若αs是奇根且ass=2,且αj也是奇根.则对所有的j≠s, ③ 若αs是奇根且ass=2,且αj是偶根,则对所有的j≠s, ④ 若ass=0,则(es)2=(fs)2=0. 以及如下的高阶Serre关系式: (其中图Ⅰ,图Ⅱ,图Ⅲ中的⊗均表示第s个位置的根) 图Ⅰ:eses-1;s;s+1+(-1)[es-1][es+1]es-1;s;s+1es=0,fsfs-1;s;s+1+(-1)[fs-1][fs+1]fs-1;s;s+1fs=0. 图Ⅱ:eses-1;s;s+1+(-1)[es-1]es-1;s;s+1es=0,fsfs-1;s;s+1+(-1)[fs-1]fs-1;s;s+1fs=0. 图Ⅲ:eses-1;s;s+1-(-1)[es-1]es-1;s;s+1es=0,fsfs-1;s;s+1-(-1)[fs-1]fs-1;s;s+1fs=0. (es+1es+q-1eses+1)Es-1;s;s+1-v2Es-1;s;s+1(es+1es+q-1eses+1)=0, (fs+1fs+q-1fsfs+1)Fs-1;s;s+1-v2Fs-1;s;s+1(fs+1fs+q-1fsfs+1)=0. 其中Es-1;s;s+1,Fs-1;s;s+1,v2见性质5. e′s+2;s+1;sE′s;s-1;s+1-E′s;s-1;s+1e′s+2;s+1;s=0,f′s+2;s+1;sF′s;s-1;s+1-F′s;s-1`;s+1f′s+2;s+1;s=0. 其中e′s+2;s+1;s,f′s+2;s+1;s,E′s;s-1;s+1,F′s;s-1;s+1见性质6. e″s;s+1;s-1-e″s+1;s;s-1=0,f″s;s+1;s-1-f″s+1;s;s-1=0. 主要研究了量子仿射李超代数的量子泛包络代数的Serre关系(含高阶Serre关系),给出了量子仿射李超代数Uq(osp(2n+1|2m)(1))的量子泛包络代数中的Serre关系的具体表达式(见定理1).计算过程具有一定的复杂性.给出的表达式对研究量子仿射李超代数的结构和表示理论都有重要的意义,例如:在文献[14]中通过Serre关系等确定了量子对应的同构表达式.此外,需要指出的是论文中给出的方法具有普遍的适用性,可以解决经典的仿射李超代数的所有Serre关系表达式.除此之外还可以找到很多其它各种李代数的结构以及同构的例子[15-16],对李代数的研究工作还有很多探索和进步的空间. 致谢作者非常感谢相关文献对本文的启发以及相关审稿专家对本文提出的指导意见.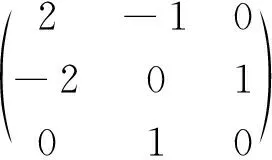

2.2 量子仿射李超代数


[Adfs+1(fs),[Adfs+1(fs),Adfs(fs-1)]v1]v2=0,
[Adfs+2(Adfs+1fs),[Adfs+1fs,Adfsfs-1]v1]=0,v1=q-(αs,αs+1);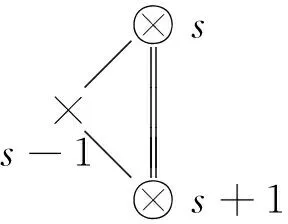
AdfsAdfs+1(fs-1)-Adfs+1Adfs(fs-1)=0,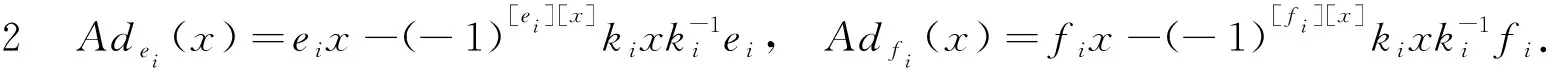
3 量子仿射李超代数Uq(osp(2n+1|2m)(1))的Serre关系
4 量子仿射李超代数Uq(osp(2n+1|2m)(1))的高阶Serre关系

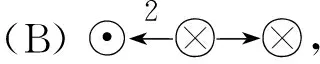

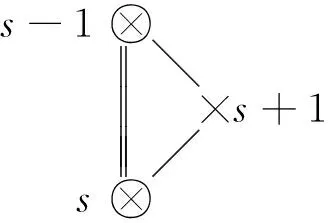
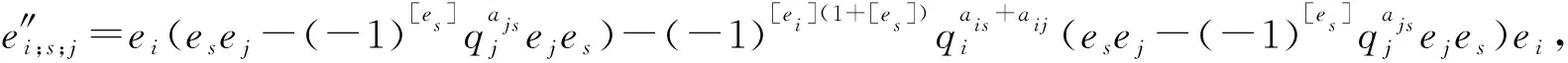
5 结 论
