离心泵动静干涉的试验及数值分析

2022-03-21闫明珠

设备管理与维修 2022年4期

闫明珠

（大庆石化公司热电厂，黑龙江大庆 163714）

0 引言

目前，动静态干扰的研究主要集中在压力脉动特性上。主要通过建立监测点和显示轴部流场来进行分析。利用PIV（Particle Image Velocimetry，粒子图像速度）技术研究了离心泵在非工作状态下由于语言分离和动静态干扰引起的流场变化。基于尺度自适应方法的数值模拟与试验相结合。不规则涡的结构与叶轮的相对位置有关。转子与定子的相互作用对线圈的晶粒压力分布有重要影响。离心泵内部流场具有明显的周期性脉动，容积的非对称性对流场的传播产生动、静态干扰。重点研究了动、静态干扰对心室区内压脉冲和湍流的影响。离心泵动静态干扰的测试方法主要有两种：试验法和数值模拟法，利用PIV 技术测量离心泵的内部流量。本文主要研究垫片区动、静态作用下叶轮的流量和脉动，结果表明当设计流量为0.2 倍时，叶轮内的流动分离得到充分发展，静态和动态扰动对电流分离的影响明显减弱。任芸等以比转速74 的离心泵为研究对象，应用像素膨胀和离心泵流动的动静态混合机理，研究叶轮容积交界处旋转表面的流动参数分布。

1 试验台简介及数值模型

1.1 试验台简介

本文采用热轧丝探头测量试验参数，试验环境为空气，试验所用离心泵比转速为26，转子处于关闭状态。利用PIV 技术研究了叶轮内不稳定流动循环的发生和发展。KSB 螺旋形的重组和加工。如果介质为空气，匹配相同的雷诺数，则其设计参数为当前试验参数。结果表明，不稳定流开始产生0.6 倍的最优条件，演变为0.4 倍的最优条件，几乎延伸整个叶轮流道0.1 倍的最优条件，车轮流量为879 m3/h，转速为3000 r/min，扬程为216 m。测量风机出口处的流量参数时，靠近叶轮流道中的电流最不稳定，将传感器置于风机出口后3 mm 处（图1）。图y 显示轴的长度，b 在蜗壳前板处为y/b=0，在后底板处为y/b=1。

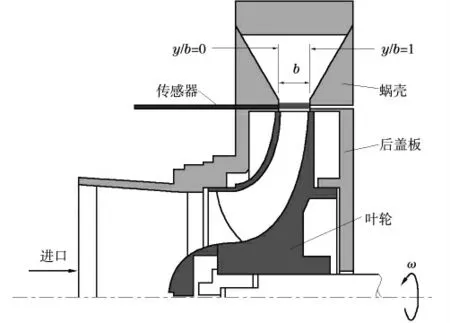
图1 试验台与泵体轴截面

由于偶然的湍流，试验过程中，流动方向的瞬时波动相对于向内方向是波动的，沿轴线方向Y/b=0.029～0.971 均匀布置17 个测点，即从间隔1.8 mm 的每2 mm 圆上各布置一个测点，得到了消除偶然湍流脉动影响后转子位置处的参数值。取测点位置，求和20～25。

1.2 数值方法介绍

速度入口用于数值模拟，速度方向垂直于入口表面，出口打开，但流动角度的波动是确定的，压力给定为101 325 Pa，选择防滑壁，如果接口稳定，则为冻结转子，因此本文采用基于叶片位置的平均法，如果接口不稳定，则是瞬态动静态滑动条件，参考压力在0.SAS 模拟中设置，以确保库仑数小于1，并且应使用数值结果验证时间周期由转子旋转所需的时间定义，采用基于有限元法的有限体积法，其中凸概念与高分辨率图离散。本研究采用ANSYS ICEM 模块对设计域（包括进水管、叶轮、容积和前后腔）进行平衡，进水管长度为进水管尺寸的5 倍，使进水管处的曲线为0，并定性地研究了静态和动态干扰对流动的影响，认为叶轮旋转对进口流场的影响可以忽略不计，从而获得相对稳定的流场。叶面、斜垫片等关键部位的网格可以进行压实，网格如图2 所示。当将实验与数值模拟进行比较时，数值模拟值基于几个循环的平均值。

图2 网格划分

2 结果分析

2.1 数值模拟验证

本文选择5 组网络（G1、G2、G3、G4、G5）来检查网络独立性。该方案综合了迎风差分和中心差分的优点，结果如表1 所示。其中包括施工条件下的系数：

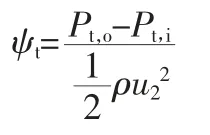
其中，Pt，o和Pt，i为泵的出口和进口总压力；ρ 是进气密度；u2是外边缘的线速度。在避免缺陷中心差振荡的基础上，利用迎风微分的优点，膨胀风微分来表示凸项。

由表1 可知，若矩形网封条数大于298 万个，采用另一类Euler 反微分来提高不确定概念的精度，方形网封条数大于43 000 个，则压头系数变化小于0.03%，复输运方程采用二阶微分来表示不确定项。考虑到成本和计算周期，本文方形网封条数引入图3（G3）。

表1 网格无关性验证

图3 是采用不同湍流模型的主要系数。径向速度很高，径向速度在垫片部隔板区域减小，这是两者之间的比较。数值模拟结果是由几个周期内不确定结果的平均值得出的。数值模拟结果与基于时间平均值的实验结果非常吻合。其中，M 是测量值，NSST是使用SST 模型的模拟值，NSAS是使用SAS 模型的模拟值。渠道中部通过时存在一定的负径向速度。SAS 模型和SST 模型的数值预测结果明显优于其他数值模型。然而，模型与试验结果之间的差异不到5%，达到了工程流体力学所需的精度，在垫片部隔板区域下游进一步减小。

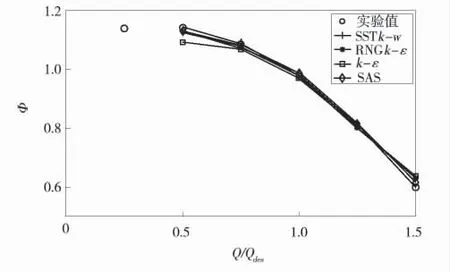
图3 扬程系数对比

图4 显示了在叶片位于叶片垫片部的情况下，压力面通过时，径向速度较高，测量旋转时压力系数CP 的比较。另外，HS表示叶轮的背面，SS 表示叶轮的正面，SAS 模型比SST 模型更精确，而且SAS 结果的分辨率更高，能更好地反映场的细节。因此，本文中包含的数值模拟值均用SAS 进行计算。

图4 回转面上压力系数分布

2.2 试验结果分析

在低流量条件下，只有当颗粒通过时，在远离叶片的位置径向速度逐渐减小，叶轮出口处的高径向速度逐渐移向通道的中心部分，容积出口之间的压力逐渐减小，定位是在隔板内侧下游有一低压区，然后移向通道的压力侧，径向速度为负，负面积随着距底部的距离而增大，可以看到在圆的位置（0-653 745）圆周很小但半径间隙很大，说明半径梯度很大，在设计流量下垫片前有一高压区，垫片两侧下游有一低压区。流场是一种强烈影响的因素，当叶轮通道靠近垫片部时，径向速度分布不均匀。叶轮流道压力面附近径向速度较高。

2.3 数值结果分析

叶轮内部压力从入口和出口逐渐升高，随着流量的增大而减小，在流量较小的情况下，压力在体积上逐渐增大，从垫片部到体积出口，在设计流量下，体积外壁的压力大于内壁的压力。高流速下的压力分布与低流速不一致，隔膜的位置和前半部分径向速度为正，在其他情况下为负。外侧和隔板垫片前有一高压区，在高流速下，垫片下游的压力区域较低，而在平均位置，舱壁下游的压力较高。