基于离心机模型试验的甘肃江顶崖古滑坡复活机理研究*

郭长宝 张永双 刘定涛 滑 帅 任三绍 李 雪 金继军

(①中国地质科学院地质力学研究所， 北京 100081， 中国) (②自然资源部活动构造与地质安全重点实验室， 北京 100081， 中国) (③中国地质科学院水文地质环境地质研究所， 石家庄 050061， 中国) (④华北科技学院， 廊坊 065201， 中国)

0 引 言

2018年7月12日，甘肃舟曲县南峪乡江顶崖古滑坡发生复活(图 1a)，新发生的滑坡体体积约(480～550)×104m3，滑坡堆积体造成白龙江南峪乡段河道堵塞、水位上涨，形成堰塞湖(图 1b)，引起国道G345线中断、淹没南峪村和南峪电站(Guo et al.，2020)，造成重大损失。近年来，包含江顶崖古滑坡在内的古滑坡复活灾害频发，造成了巨大损失，进一步引起了研究者对古滑坡变形和灾害研究的重视。穆鹏(2011)认为江顶崖古滑坡具有显著的分级分块滑动特性，降雨、滑坡区高陡的地形、河流冲刷及不良的岩土体工程地质性质是该滑坡复活的主要因素。古滑坡一般指第四纪以来滑动过的滑坡，是斜坡长期复杂演化过程的产物，古滑坡现今多处于基本稳定状态，但有可能发生复活或再次滑移(戚筱俊， 2002； 张永双等， 2018)。古滑坡复活可能是受自然因素影响发生的，如降水、河流侵蚀、地震等引起古滑坡复活，也可能是人类工程活动诱发的。古滑坡复活极易造成重大经济损失，如在20世纪50年代，陇海铁路西安—宝鸡段卧龙寺老滑坡复活，体积约2.0×107m3，将陇海铁路向南推移100多米(张茂省等， 2011)； 在20世纪90年代中期，南昆铁路八渡车站古滑坡发生复活，治理费用达9000余万元(王恭先等， 2004)； 2014年美国华盛顿州OSO古滑坡发生复活，复活体积达760×104m3，掩埋了高速公路SR530，滑坡造成43人死亡(Iverson， et al.，2015)等等，古滑坡复活现象为世界范围内关注的重要研究内容和难题(黄润秋等， 2007；Sassa， et al.，2013； 张永双等， 2018)。

国内外研究者对古滑坡复活机理开展了大量研究，主要研究方法有：物理模拟、工程地质分析和数值模拟等。物理模拟是采用相似材料，通过模拟斜坡演变过程中有关因素的改变来再现斜坡变形破坏过程，进而分析其力学机制和变形破坏机制(张云祥， 2010； 赵建军等， 2019； 晏长根等， 2021)，该类试验对揭示滑坡变形破坏过程最为直观。由于普通的室内小尺寸模型试验，无法模拟真实的应力场而引起重力失真，造成试验结果与实际值有较大偏差，而离心机试验能弥补这方面的不足。由于土工离心模型试验能再现自重应力场以及与自重有关的变形过程而具有独特的优点，成为与原型相似性较好的古滑坡复活力学模型试验方法，在滑坡灾害成灾机理中得到了广泛应用(冯振， 2012； 吴昊宇等， 2015)。因此，为了深入研究江顶崖古滑坡2018年的复活机制，本次通过离心机物理模拟，研究了江顶崖滑坡在不同含水率下复活变形发展过程、滑坡破坏过程中位移场演化趋势、滑坡体内部应力-应变响应规律及孔压增长模式等关键性问题，进而提出江顶崖古滑坡复活的成因机制，对于区域防灾减灾和古滑坡复活机理研究具有一定的指导意义。

1 江顶崖古滑坡基本特征

1.1 地质背景

江顶崖古滑坡位于甘肃省舟曲县城东南侧白龙江左岸炭窑山下，也被称为南峪滑坡(陈洪天， 1991； 王景荣等， 1994； 焦赟等， 2011； 穆鹏， 2011)，该流域内地质构造和地形地貌极为复杂、历史强震发育，大型滑坡和泥石流等地质灾害极为发育。受活动断裂、历史强震、降雨和人类工程活动等因素的影响，近年来该区曾发生过甘肃舟曲2010年8月8日泥石流灾害(胡向德等， 2011； 孟兴民等， 2013)，江顶崖滑坡1991年、2007年和2010年3次发生大规模复活(焦赟等， 2011)、泄流坡滑坡多次复活滑动(黄晓等， 2013； Jiang et al.，2016)等极为严重的灾害事件。

图 2 江顶崖古滑坡工程地质剖面图Fig. 2 Engineering geological section of Jiangdingya ancient landslidea. 滑坡侧壁滑带与基岩出露关系； b. ZK3钻孔揭露滑带土特性

1.2 古滑坡复活特征

江顶崖古滑坡全长640～700m，宽度240～250m，体积(640～970)×104m3(图 2)。江顶崖古滑坡自1807年发生大规模滑动(陈洪天， 1991)以来，曾多次发生复活，造成白龙江堵江断流，之后经常发生滑动； 20世纪以来，比较明显的是1985年在江顶崖古滑坡体上出现滑坡征兆，并于1986年、1988年、1990年、1991年和2018年分别发生大规模滑动，后4次还发生堵江事件，造成了极为严重的损失。

2018年，江顶崖滑坡复活滑体呈长舌型，纵长约580m，前缘宽约300m，中部宽约190m，后缘宽约185m，面积约0.12km2，在滑体侧壁可见清晰滑动剪切带与出露基岩(图 2a)，钻探揭露厚层滑带(图 2b)，滑体平均厚度约40～50m，体积(480～550)×104m3。滑坡的发生受降雨影响大，Guo et al.(2020)研究认为滑坡发生滑动时其滑带含水率为14.03%，是在强降雨作用下诱发形成的滑坡。

2 江顶崖古滑坡离心机模型试验

2.1 土工离心机试验原理

土工离心模型试验是将模型进行一定比例缩尺后置于离心机中，再按相同比例将重力加速度进行放大后所得的离心加速度进行试验(王锴， 2020)，由于惯性力和重力的高度等效性，从而使得模型和原型的应力、应变相等，变形相似，破坏机理相同，再现原型变形破坏过程。其基本原理为：将按比例缩小的物理模型放置在高速旋转的大型土工离心机中，模型在试验过程中将受到较高的离心加速度影响，当离心加速度大小合适时，模型所产生的离心力正好可以用于补偿地质模型因缩小比尺带来的自身重力损失(Bowman E T et al.，2010)。

离心机最早于1973年应用于岩土工程等方面的研究，美国学者Buky利用离心机开展矿山结构物破坏的相关研究。目前，土工离心机已广泛应用于软土地基固结、沉降与承载力问题、黏土边坡稳定性研究，以及挡土墙、隧道、涵管、土石坝、近海平台等许多土与结构物互相作用的研究中(魏迎奇等， 2018)，并取得了重要进展，如离心机振动台揭示了强震作用下的边坡倾倒变形、土质滑坡变形机制和动力响应规律(巨能攀等， 2019； 黄珮伦等， 2020)； 超大直径盾构隧道动态掘进过程对地表城际铁路沉降影响(杨林松等， 2021)； 揭示了不同加密型抗液化处理的小型土石坝边坡地震响应规律(刘庭伟等， 2020)。

2.2 试验设备

本次试验采用成都理工大学地质灾害防治与地质环境保护国家重点实验室的TLJ-500土工离心试验机(图 3)。该试验机由离心机主机、900kW直流电机、数据采集及传输系统、拖动系统、监视系统、数据处理系统、模型箱及机械手等系统组成，最大容量500g·t、最大离心加速度可达250g，模型箱最大尺寸为1.2m(长)×1.0m(宽)×1.2m(高)(表 1)。

图 3 TLJ-500型土工离心机Fig. 3 The TLJ-500 geotechnical centrifuge

表 1 TLJ-500型土工离心机主要参数Table 1 Main parameters of TLJ-500 geotechnical centrifuge

2.3 滑坡物理模型

2.3.1 滑坡原型

本次滑坡物理模拟主要是反演分析2018年滑坡复活启滑机理，模拟范围主要为2018年的复活区域(图 4)。

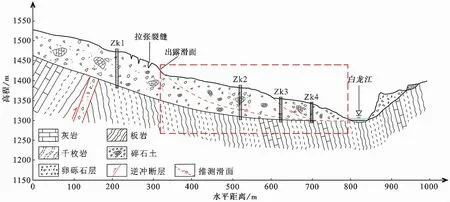
图 4 江顶崖古滑坡工程地质剖面图(虚线框为本次离心机模拟滑坡范围)Fig. 4 Engineering geological section of Jiangdingya ancient landslide(the dashed box simulates the landslide range for this centrifuge model test)

2.3.2 离心机模型比尺及结构

模型比尺的选择需要综合考虑原型的大小、离心机的容量、模型箱的尺寸、研究问题的性质和模拟精度等。若要模拟江顶崖古滑坡原型和滑坡区范围，则其水平距离接近600m，滑坡宽度最大为300m(前缘)，滑坡高度达到180m，而试验模型箱最大尺寸为1.2m(长)×1.0m(宽)×1.2m(高)，相似材料密度和模型质量均无法满足试验要求，综合考虑模型尺寸和原型条件，设计模型尺寸长宽高为1.0m×0.5m×0.3m，模型比尺n=600。离心机模型与滑坡原型主要物理量的相似比见表 2。在制备模型时，模型的物理量严格按照相应的相似比尺寸设计。根据滑坡原型结构，模型结构主要包括滑床、滑体和滑带。

表 2 离心机模型与原型相似比Table 2 Similarity ratio of centrifuge model and prototype

2.4 试验工况

根据笔者2018年7月22日现场调查与取样测试结果，滑坡体后缘出露地表的滑带表层含水率为9.74%，后缘地表以下0.5m位置处滑带含水率为20.76%，在Zk3钻孔(图 2b)29.8m位置处滑带土含水率为14.03%(郭长宝等， 2019)，其中钻孔位于滑体中前部，滑坡在剪切过程中发生排水现象，其含水率低于滑体后缘滑带土的含水率，滑体后缘地表下含水率更接近于江顶崖滑坡启滑时的坡体含水率。因此，为了揭示江顶崖古滑坡复活变形发展过程，采取滑坡现场滑体和滑带材料进行重塑，分别配制接近于滑坡后缘地表、地表以下0.5m和钻孔深部滑带土不同含水率(10%， 15%， 20%)江顶崖滑体离心机模型来研究江顶崖古滑坡的复活机理。在试验过程中，逐渐提高加载离心加速度来模拟滑坡失稳现象，试验工况如表 3所示。试验过程主要分为固结阶段、变形失稳阶段或趋于稳定阶段。

2.5 模型材料的力学参数

2.5.1 滑床材料

江顶崖滑坡滑床主要由炭质板岩、千枚岩、砂岩夹灰岩构成。在制作离心模型前，先确定相似材料的选择及配比，通过相似三定理、离心模型试验主要比尺关系，参考前人相似材料研究成果，最终确定滑床采用重晶石粉、碎石、石英砂、石膏和水按照一定重量配合比拌合制作(李光等， 2019； 郑达等， 2019)(表 4)。

表 4 滑床相似材料配比表Table 4 Proportioning table of similar materials for sliding bed

表 3 离心机模型试验方案Table 3 Centrifuge model test plans

2.5.2 滑体、滑带材料

为能够真实反映滑坡原型岩土体的物理力学特性，本次试验滑体和滑带采用滑坡现场原型材料来制作，并根据现场材料级配进行粒组配比，对配比材料进行物理力学试验，以使滑体材料和滑带材料力学参数与现场接近(表 5)。

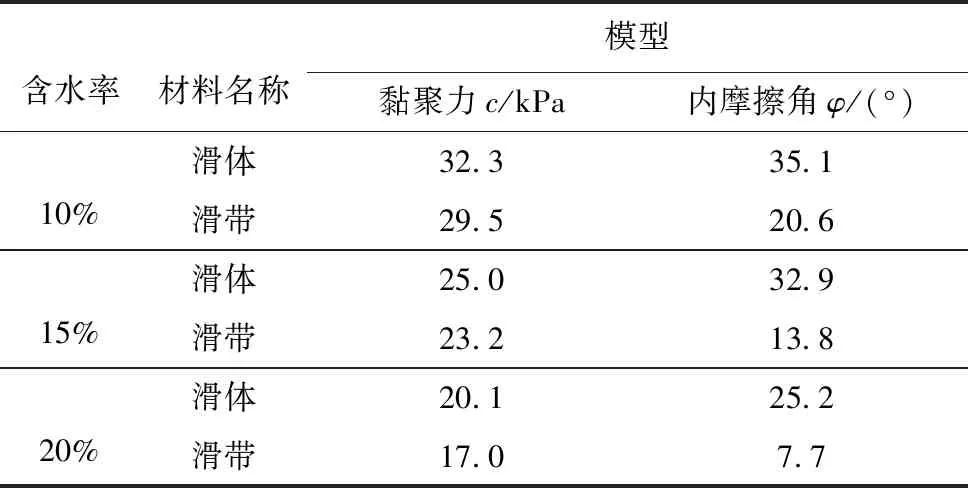
表 5 滑体及滑带力学参数取值Table 5 Values of mechanical parameters of sliding body and sliding belt

2.6 传感器的类型及埋设

参考以往离心机模拟试验的经验和成果，本次离心机模拟试验监测仪器采用中国工程物理研究院总体工程研究所研发的高速离心机专用土压力传感器(TY1008)、孔隙水压力传感器(KY1008)和多角度摄像头(图 5)，通过线缆与控制系统相连。监测传感器布设原则具体如下。

图 5 传感器布设点位图Fig. 5 Layout of sensors for the test

(1)土压传感器布置：主要布置在滑带内，由上至下分别布置4个土压传感器TY-1、TY-2、TY-3、TY-4，另在滑体后缘(TY-5)、中部(TY-6)及前缘(TY-7)各布置一个土压传感器，土压传感器的量程为1MPa，其直径为1.4cm。

(2)孔隙水压力传感器布置：主要布置在滑带内，由上至下分别布置3个孔压传感器KY-1、KY-2、KY-3，孔压传感器的量程为500kPa，其直径为1.4cm。

(3)多角度摄像头，实时对滑坡模型变形进行高清摄像和坡表位移的捕捉。

图 8 LST-1模型在含水率为10%时的坡表裂缝发育过程图Fig. 8 The development process of cracks on the slope surface of the LST-1 test model when the water content is 10%a. t=9min， 加速度=50g； b. t=15min， 加速度=60g； c. t=16min， 加速度=80g； d. t=18min， 加速度=100g； e. t=19min， 加速度=120g； f. t=28min, 加速度=150g

2.7 离心机模型制作过程

离心机模型制作过程主要有观测网格制作(图 6)、滑床制作、滑体与滑带(软弱层)制作，制作好的模型如图 7所示。

图 6 观测网格制作Fig. 6 Completed observation grid

图 7 制好的江顶崖滑坡模型图Fig. 7 Completed model of Jiangdingya landslide

3 离心机试验结果分析

3.1 滑坡模型破坏特征

图 9 LST-2模型在含水率为15%时的坡表裂缝发育过程图Fig. 9 The development process of cracks on the slope surface of the LST-2 test model when the water content is 15%a. t=7min， 加速度=30g； b. t=9min， 加速度=40g； c. t=10min， 加速度=50g； d. t=12min， 加速度=60g； e. t=14min， 加速度=80g； f. t=19min, 加速度=100g

图 10 LST-3模型在含水率为20%时的坡表裂缝发育过程图Fig. 10 The development process of cracks on the slope surface of the LST-3 test model when the water content is 20%a. t=3min， 加速度=8g； b. t=4min， 加速度=9g； c. t=5min， 加速度=13g； d. t=6min， 加速度=20g； e. t=7min， 加速度=30g； f. t=12min, 加速度=50g

如图 8 所示，在LST-1试验中，滑体含水率为10%的情况下，试验结束后仅在坡体中后部产生少量裂缝，但在整个试验过程中滑坡体并没有产生滑动破坏。由图 9可知，在LST-2试验中，含水率为15%的情况下，试验进行至9min离心加速度达到40g时，坡体中后部开始产生裂缝，随着离心加速度增加至50g，裂缝逐渐发展，裂缝总体为弧形分布，呈拉裂性质，当离心加速度从60g增加至100g，裂缝逐渐向前缘发展贯通，最终造成滑坡的整体滑动。由图 10可知，在LST-3试验中，含水率为20%的条件下，试验仅进行至3min离心加速度仅为8g时即开始产生裂缝，离心加速度仅增加1g(即达到9g)时，裂缝便迅速发展，试验进行至5min离心加速度为13g时，裂缝已经向前缘发展贯通，前缘土体在受到后缘土体挤压情况下，前缘土体发生土体膨胀现象，随着离心加速度不断增加，坡体持续滑动破坏。

3.2 土压力变化分析

(1)据图 11a分析，在含水率为10%的情况下，离心加速度加载至150g之前，土压力计读数随着离心机加速度增加整体上逐渐增大，滑坡体与离心加速度呈现线性相关性和跳跃性，表明坡体处于稳定状态。TY-5和TY-7的读数在离心机加速度逐渐加载至150g后增长缓慢，TY-5和TY-7最大读数分别为31.36kPa和34.77kPa，这表明滑坡体在中后部和前缘已有微略变形的趋势，由图 8a可以看出此时滑坡体产生少许裂缝，但坡体整体还处于稳定状态。

(2)据图 11b分析，在含水率为15%的情况下， ①离心加速度0～45g阶段，土压计读数变化趋势与离心加速度变化趋势一致； ②离心加速度45～60g阶段，即坡体开始产生裂缝阶段，在试验进行至9min和11min时，TY-2和TY-4读数突然下降，由图 9裂缝发育过程可知，此时坡体产生裂缝造成了土压力的读数下降； ③离心加速度60～100g阶段，坡体处于裂缝迅速发育扩展阶段，此时土压计读数平均增长率不断增大，表明离心加速度产生微量的增加，土压力的读数便迅速增大，由图 9可知，在这一阶段坡体产生的裂缝在很短的时间内就迅速发展； ④离心加速度维持100g阶段，坡体处于失稳状态，在试验进行至19min时，TY-5读数突然下降，而试验进行至20min时，TY-6读数才突然下降，TY-6读数下降滞后于TY-5，该现象说明滑坡变形破坏从中后缘开始，并逐渐向滑坡前缘发展，坡体已达到失稳状态，推测其为推移式滑动。

(3)据图 11c分析，在含水率为20%的情况下， ①离心加速度10～30g阶段，裂缝处于发展阶段。TY-3、TY-4读数增加的趋势基本一致，当试验进行至10min时，TY-3和TY-4读数增加趋势逐渐大于TY-2，随着离心加速度逐渐增大，TY-3和TY-4读数增加趋势更为明显。该现象说明随着裂缝从中后缘开始产生，滑坡后部的推力在不断地增加，且不断地向滑坡前缘传递，导致滑坡前缘的土压力增幅更为明显； ②离心加速度30～50g阶段，坡体处于失稳状态，随着离心加速度不断增加，滑坡后缘推力不断向滑坡前缘增加，造成裂缝不断向前缘扩展，最终造成滑坡的整体滑动破坏。

图 11 不同含水率下土压力随加速度变化趋势图Fig. 11 Trend graph of earth pressure with acceleration under different water contenta. 含水率为10%； b. 含水率为15%； c. 含水率为20%

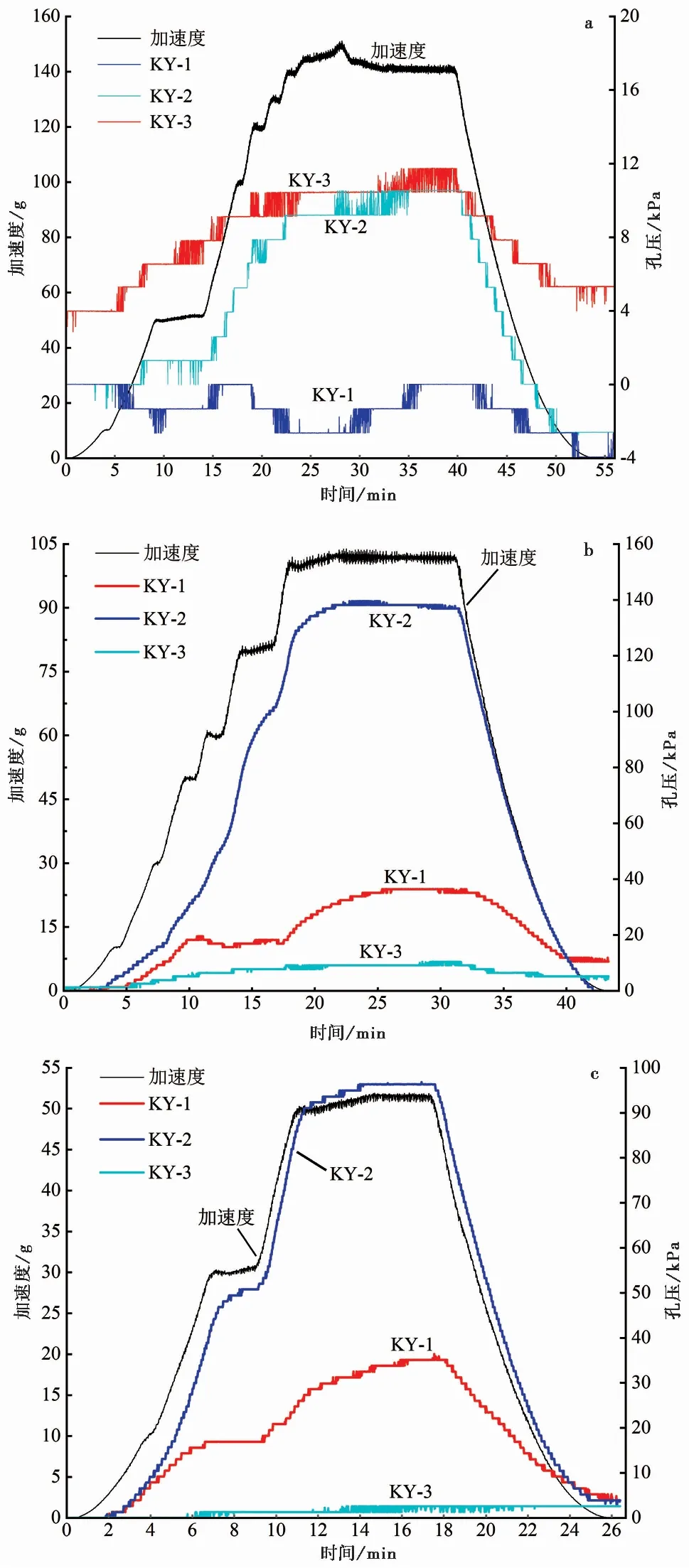
图 12 不同含水率孔隙水压力随加速度变化趋势图Fig. 12 Trend graph of pore pressure with acceleration under different water contenta. 含水率为10%； b. 含水率为15%； c. 含水率为20%

3.3 孔隙水压力变化分析

本次试验一共布置了3个孔隙水压力计，孔隙水压力计具体位置如图 5所示，以此来分析KY-1、KY-2、KY-3的变化。

(1)据图 12a分析，在含水率为10%条件下，KY-1的读数一直呈现负增长，最大孔隙水压力为-4kPa，这表明该处滑坡体为非饱和土体，水体主要沿着颗粒向土体内部渗透，土体颗粒之间存在水-气弯液面(陈洪凯等， 2017)，所以测得的孔隙水压力为负值； KY-3读数大于KY-2，在试验进行27min时，KY-2读数突然增加，最大至11.74kPa，而KY-3读数大小滞后于KY-2，在试验进行到32min时KY-3读数突然增大，最大增加至10.55kPa。表明在试验过程中滑坡体产生向前的挤压，中后缘开始产生裂缝使滑体内水分向前缘流动，使孔隙水压力突然增加。由图 11a的土压力变化趋势图可知，TY-5率先发生变形破坏，导致孔隙水往KY-3位置汇集，造成KY-3的读数升高。在加速度维持在140g的时间段内，孔隙水压力先保持不变后突然增加，表明在此过程中滑坡体产生位移变形挤压，滑坡中后缘产生少量裂缝使水分向前缘流动，使其孔隙水压力逐渐增加。

(2)据图 12b分析，在含水率为15%条件下，KY-2读数随加速度成比例升降，KY-2读数明显大于KY-1，表明在试验过程中滑坡体产生向前的挤压变形破坏。试验在60～100g阶段时，KY-1的读数由19.53kPa缓慢减小至15.66kPa。试验在加速度维持100g阶段，KY-2读数逐渐增大，最大可达138.21kPa，由图 11b土压力变化趋势及图 10滑坡裂缝发育过程图可知，此时坡体中后部已产生裂缝，坡体中后部的水沿着裂缝往坡体前缘汇聚，造成KY-1读数上升。

(3)据图 12c分析，在含水率为20%条件下，从加速度增加至8g开始，KY-2读数大于KY-1读数，而从图 11a坡表裂缝发育图可知，此时坡体已经开始从中后部产生裂缝，后部土体向前挤压，造成KY-2读数大于KY-1读数。加速度达到50g，试验进行至15min时，KY-2达到最大值96.35kPa，此时坡体已经开始处于失稳阶段，在加速度维持在50g的时间段内，KY-1和KY-2的增长率缓慢直至趋于平缓，表明滑体在小离心荷载的作用下，产生位移变形挤压，坡体处于失稳状态，造成孔隙水压力读数也发生明显的变化。

3.4 江顶崖古滑坡复活启滑过程分析

3.4.1 滑带土力学强度变化分析

为了分析滑带土力学强度的变化，在LST-3试验含水率为20%情况下对滑坡滑动前后的滑带土进行直剪试验，破坏前滑带土黏聚力c值为17kPa，破坏后为12kPa； 破坏前内摩擦角φ为7.76°，破坏后为5.58°。由此可见滑动后土体较滑动前黏聚力c减少了5kPa，衰减了29.41%； 内摩擦角φ减少了2.18°，衰减了28.09%。由此可知，滑坡模型在含水率为20%情况下，滑坡的变形大幅减弱了滑带土的力学参数，诱发了滑坡的产生。

3.4.2 滑坡变形过程分析

试验表明，江顶崖滑坡的变形受含水率的控制，坡体的变形破坏是由中后部逐渐发展的，随着坡体含水率的增加，滑坡启滑所需的加速度就越小。在含水率分别为15%情况下，开始产生裂缝的离心加速度为40g，失稳时的离心加速为100g，而在含水率分别为20%情况下，开始产生裂缝的离心加速度为8g，失稳时的离心加速为50g。根据试验分析滑坡的变形过程主要分为以下3个阶段： ①变形启动阶段，在此阶段坡体中后部裂缝开始产生； ②变形加速阶段，在此阶段中后部裂缝迅速发育，并迅速扩展至坡体前缘； ③失稳阶段，在此阶段，坡体表面拉张裂缝扩展贯通，潜在滑移面形成，整体发生失稳滑动。

4 江顶崖古滑坡复活机理讨论

江顶崖古滑坡复活机理复杂，在断裂活动和地震作用下形成的破碎岩土体和斜坡结构特征为滑坡复活提供了内因，强降雨作用增加了坡体的自重并弱化了岩土体的力学强度，在暴雨期形成的强烈河流侵蚀作用进一步切割了坡脚，从而诱发了滑坡的复活，其是在内外动力耦合作用下形成的典型古滑坡复活(郭长宝等， 2019)。根据离心机物理模拟试验结果，结合野外调查，以及已有Guo et al. (2020)等的调查分析，本文认为降雨作用造成江顶崖古滑坡中后部含水率升高，中后部产生拉裂缝随后产生推移滑动，并且受到前缘河流侵蚀牵引情况下，形成了前缘河流侵蚀牵引、滑坡中后部推移的耦合启滑机制，最终造成江顶崖古滑坡的复活。

4.1 降雨对古滑坡复活的影响

降雨是诱发大型滑坡的主要因素之一，Ren et al.(2013)认为当甘肃舟曲地区降雨量达到30mm时将会非常容易诱发大型滑坡； 代聪等(2021)认为江顶崖滑坡在2018年7月11日～2018年7月12日降雨量达28mm，达到全年最高峰，最终导致了江顶崖滑坡整体失稳。郭长宝等(2019)认为在7月10日降雨量更是达到了65mm的暴雨级别； Lumb(1962)发现当24h内降雨量超过100mm或先前15d内降雨量超过350mm时，易诱发滑坡，而江顶崖6月25日～7月10日15d内累计降雨量已超过300mm。由于江顶崖滑坡体结构松散，且裂缝较多，强降水很容易通过裂缝，形成入渗通道，降雨入渗到滑带内，增加了滑带土的含水率，软化了滑带土的力学强度，同时入渗的降雨在相对隔水层(炭质板岩)形成上层滞水，增加了岩土体自重，增大了下滑力，最终导致滑坡的发生。

4.2 滑坡变形过程中的超孔隙水压力对滑坡启滑的影响

滑坡启滑的临界孔隙压力主要由斜坡岩土体的密度、有效孔隙度、潜在滑移面上覆岩土体厚度、斜坡组成物的黏聚力和内摩擦角及斜坡的坡角决定(麻土华等， 2014)。

(1)

式中：θ为滑坡上存在着一个倾斜的软弱层面的倾角(°)；ρ为岩土体的密度(g·cm-3)；g为重力加速度；z为潜在滑移面的深度(即上覆岩土体厚度，m)；c为岩土体的黏聚力(kPa)；φ为岩土体的内摩擦角(°)。根据式(1)，θ取30°、ρ取 2.16 g·cm-3、g取9.8m·s-2、z取0.3m、c取27kPa、φ取30.5°可求得临界孔隙压力Uwc=67.27kPa，在滑体含水率为10%的情况下，最大孔隙水压力为11.77kPa，小于临界孔隙水压力，而试验在15%和20%情况下最大孔隙水压力分别为138.21kPa和96.35kPa，均超过了临界孔隙水压力Uwc，最终引起了滑坡滑动。

5 结 论

本文以甘肃江顶崖古滑坡复活为原型，在野外调查基础上开展了其复活过程的离心机模型试验，得到以下主要结论和认识：

(1)结合离心机模拟试验与野外调查分析，强降雨是导致江顶崖古滑坡复活的直接原因，强降雨入渗导致滑带土体力学强度降低，并在前缘河流侵蚀耦合作用下，形成后部推移-前缘牵引复合式启滑机制。

(2)模拟了不同含水率下滑坡启滑过程，获得了滑坡破坏时土压力、孔隙水压力变化规律，试验表明坡体的变形破坏是由中后部逐渐发展的，随着含水率的增加，滑坡启滑所需的离心加速度就越小。在含水率为15%、20%情况下坡体失稳所需离心加速度分别为100g和50g，而在含水率为10%情况下，试验结束后仅在坡体中后部产生了少量裂缝，与实际情况相符。

(3)试验表明江顶崖古滑坡的复活变形过程主要分为3个阶段： ①变形启动阶段(裂缝开始形成阶段)； ②变形加速阶段(裂缝发展阶段)； ③失稳阶段。

(4)降雨是导致古滑坡复活的主要原因，降雨引起土体含水率的变化，一定程度上降低了土体强度，并导致土体中孔隙水压力发生变化，降低了土体的抗滑力，进而降低了坡体的稳定性，导致滑坡的形成。

致 谢本次试验测试在成都理工大学地质灾害防治与地质环境保护国家重点实验室完成，任洋副教授、郑光副教授对本次试验进行了指导； 中国地质科学院地质力学研究所杨志华副研究员、中国地质大学(北京)刘健硕士生参加了野外工作，在此一并表示感谢。