基于三点公式的直角四面体优化模型

向枫桦，杨宾峰，赵 震，李 博，郭娇娇

(空军工程大学信息与导航学院，陕西 西安 710077)

0 引言

磁场具有抗干扰能力强、穿透性强等优势[1]，在室内、水下、地下以及人体这些特殊环境中作用尤为突出[2-4]，已经成为一个研究热点，涉及磁场的技术主要有磁传感器技术[5]和磁测量技术[6]。

常见的磁传感器模型有平面模型和立体模型，平面模型主要有三角形、正方形和十字形等传感器模型，立体模型主要有直角四面体、正四面体和正六面体等结构。三角形传感器的设计思想属于两点公式，由于两点公式误差较大，因此该结构测量精度不高[7]。正方形传感器采用三点公式中的端点公式，由于三点公式优于两点公式，因此该结构测量精度优于三角形结构，但是在z轴方向误差较大[8]。十字形传感器采用三点公式中的中点公式，由于中点公式优于端点公式，因此该结构测量精度优于正方形结构，但是同样在z轴方向误差较大[9]。直角四面体传感器虽然可以充分利用每个轴上的磁场信息，但是由于采用两点公式，因此整体误差较大[10]。正四面体传感器运用差分方程进行求解，虽然方法新颖，但是最后的测量精度同样不高[11]。正六面体传感器采用三点公式中的端点公式设计思想，虽然充分利用了三个轴上的信息，但是测量点与磁偶极子位置偏差较大，测量精度同样不高[12]。总之，传统传感器模型存在误差大或者无法充分利用z轴磁场信息的问题。本文针对此问题，提出基于三点公式的直角四面体优化模型。

1 磁场梯度张量与数值微分基础

1.1 梯度张量矩阵

磁梯度张量(magnetic gradient tensor ,MGT)蕴含了大量的磁场信息[13]。MGT是磁场梯度测磁技术的扩展和发展，磁感应强度的三分量在三个方向上的分量变化率就是磁梯度张量矩阵，磁梯度张量矩阵一共有9个元素[14]，记作G，如下式：

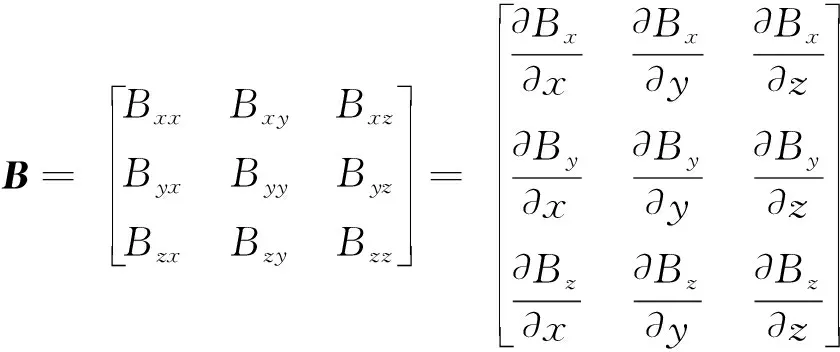
(1)

根据Maxwell方程组，磁感应强度的散度和旋度均为0，可以推出：

(2)

然后可以得出如下结论：

(3)

在式(3)中，可以看出梯度张量矩阵中的9个量只有5个独立的元素。

1.2 梯度张量矩阵理论值计算

任意一点A(x,y,z)的磁场三分量为：

(4)

在式(4)中，可以看出Bx和By是关于x和y的轮换对称多项式。

将式(4)中的磁场三分量分别求偏导数，得到理论上的独立的五个磁梯度张量的表达式为：

(5)

1.3 数值微分基础

如果一个函数f(x)满足Δx=xk+1-xk=xk+2-xk+1足够小这个条件时，并将这个函数记为f(x)=f(xk)。

则有：

1)两点公式：

(6)

(7)

2)三点公式：

①端点公式：

(8)

(9)

②中点公式：

(10)

2 基于三点公式的直角四面体模型

2.1 直角四面体模型

传统直角四面体模型一共4个传感器，每个轴上都分布两个传感器，相邻传感器之间的距离相等，如图1所示。

图1 直角四面体传感器模型Fig.1 Right-angle tetrahedral sensor model

根据两点公式，得到MGT的独立元素表达式为：

(11)

2.2 基于端点公式的直角四面体模型

由于端点公式需要用3个点来计算导数，因此每个轴上需要3个传感器。如图2所示，该模型一共7个传感器，每个传感器的型号大小一样，每个轴上都分布3个传感器，相邻传感器之间的相等，大小均为d。

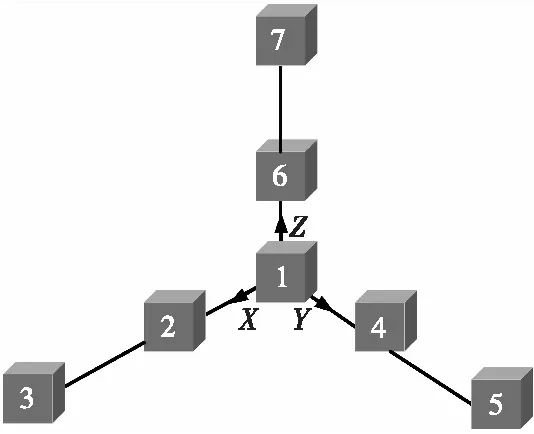
图2 基于端点公式的传感器模型Fig.2 Sensor model based on endpoint formula

根据端点公式，得到MGT的独立元素表达式为：

(12)

2.3 基于中点公式的直角四面体模型

如图3所示，该模型一共6个传感器，每个轴上都分布2个传感器，相邻传感器之间的距离相等，大小为d。

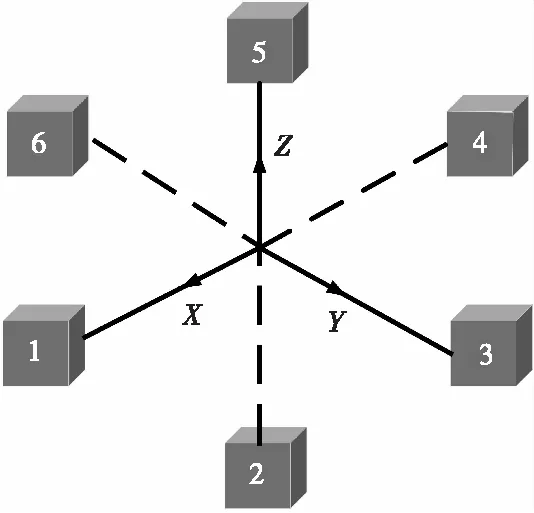
图3 基于中点公式的传感器模型Fig.3 Sensor model based on midpoint formula

根据中点公式，MGT的独立元素表达式为：

(13)

在式(13)中，由于该模型既可以测量出Bxy，又可以测量出Byx，并且两者的值大小不一样，为了充分利用磁场的信息，因此，对于Bxy是取两者的平均值，其他量也类似。

3 仿真分析与优化设计

3.1 测量阵列

利用Matlab软件，对基于中点公式和基于端点公式的测量阵列进行理论仿真。以磁偶极子为原点建立三维坐标系，采样阵列为81个点，其中z轴的距离恒定为1 m，x轴从-2 m到2 m，间隔为0.5 m，取9个点、y轴从-2 m到2 m，间隔为0.5 m，也取9个点，建立如图4所示的一个9×9的方格测量阵列。

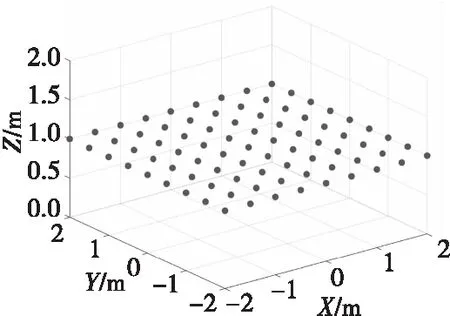
图4 测量阵列分布Fig.4 Measurement array distribution

3.2 不同传感器模型的对比

为了比较不同传感器模型的测量精度，在上述的测量阵列上对MGT中的5个独立元素进行仿真计算，并与理论值进行对比分析，在Matlab中分别得到基于端点公式和中点公式的独立元素分布图，如图5所示。

在图5中：基于中点公式的传感器模型的独立元素分布曲线基本上与理论曲线一致；基于端点公式的传感器模型独立元素分布曲线与理论曲线在曲线形状和曲线宽度上不一致。

为了进一步比较传感器模型的精度，引入了常见的精度最高的十字形传感器模型，与基于三点公式的两种改进型模型进行对比分析。

相对误差计算公式：

(14)

得到的相对误差分布如表1所示。

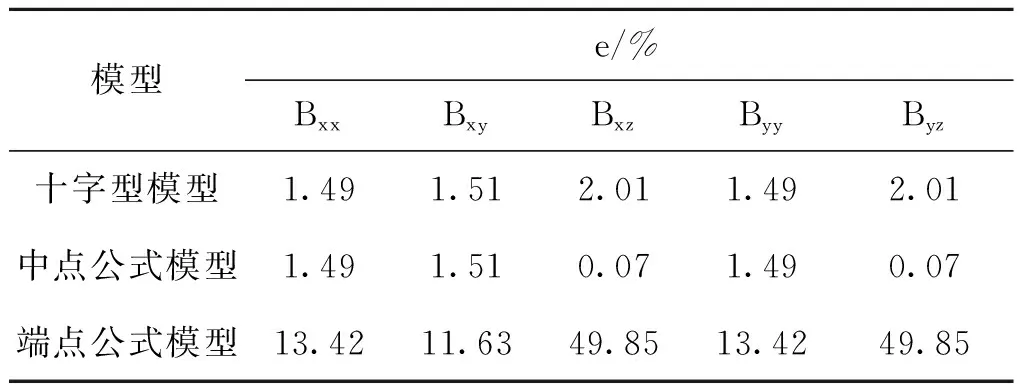
表1 不同模型传感器的相对误差对比Tab.1 Error comparison of different model sensors

在表1中，基于中点公式的传感器由于在x-y平面的设计与十字形相同，因此两者的定位精度一样，但是由于增加了z方向的传感器，因此，在z方向上测量精度更高。

选取效果最好的中点公式模型，仿真得到的三维分布图如图6所示。

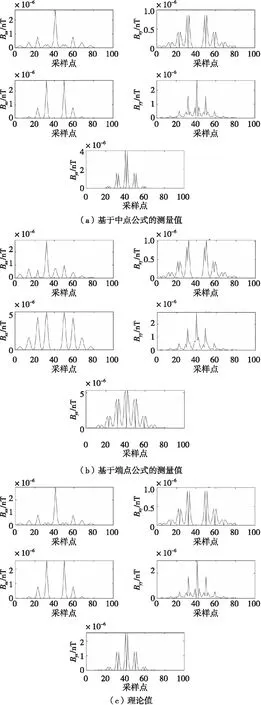
图5 独立元素的对比图Fig.5 Contrast figure of individual elements

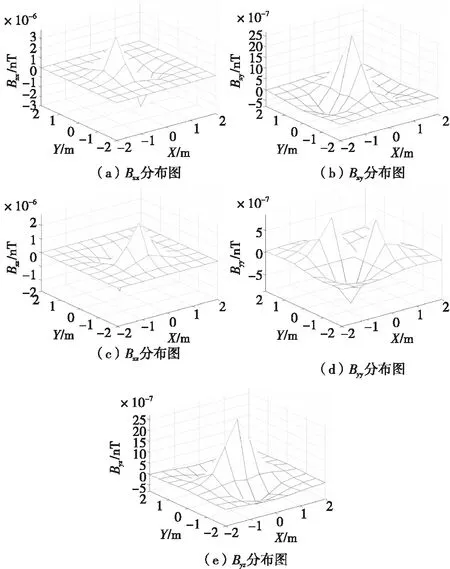
图6 三维分布图Fig.6 Three-dimensional distribution

在图6中，Bxx关于x轴对称，Bxy关于x轴和y轴平分线对称，Bxz关于x轴和z轴平分线对称，Byy关于y轴对称，Byz关于y轴和z轴平分线对称。

3.3 目标函数构建

将磁场三分量以函数形式表示为：

(15)

在基于中点公式的传感器中，不再以等距建立模型，在x，y轴上，增加一个偏量ad，z轴方向增加一个偏量bd，同时保持同一个方向的传感器的距离为2d，建立的磁场梯度的5个独立元素的误差函数如下。

构建以下这个优化模型，在-1～1范围内，求解f(a,b)的最小值，具体模型如下所示：

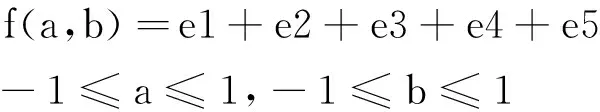
(16)

(17)

3.4 亲和力计算

亲和力计算公式为：

(18)

式(18)中，tk是抗原和抗体k的结合强度。

结合强度tk采用海明距离计算，表达式为：

(19)

3.5 免疫克隆算法实现流程

步骤1 初始化

设置免疫个体的维数为2，最大免疫代数为200次，免疫范围的上限为1、下限为-1，免疫初值为0，相似度阈值为0.2，变异概率为0.7以及目标函数为f(a,b)等。

步骤2 计算个体浓度和激励度

分别对个体进行浓度和激励度计算，并将激励度按升序排列。

步骤3 免疫循环

免疫循环阶段不断计算亲和度和免疫种群激励度，对抗体进行促进和抑制，保留亲和度最高的个体[16]。

步骤4 群体更新

再生新种群的刺激度，使免疫种群与新种群融合。

3.6 仿真分析

在200次的迭代运算后，目标函数达到了一个最优值为1.262 6×10-9，其中a为-8.157 4×10-2，b为6.813 4×10-2，迭代曲线如图7所示，将优化后的算法与前面基于中点公式的模型进行对比，如表2所示。

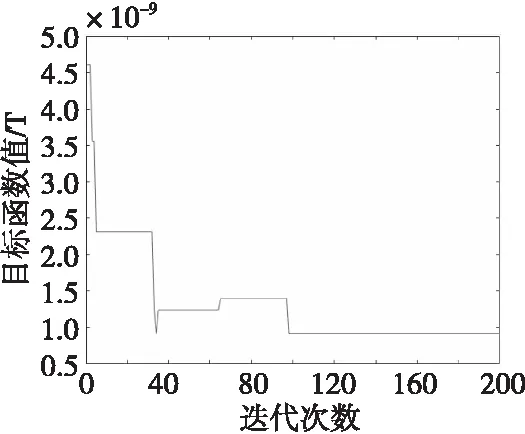
图7 亲和度进化曲线图Fig.7 Affinity evolution curve

在图7中，经过200次的迭代运算后，目标函数的值达到了一个最小值，此时就可以得到最佳优化模型。

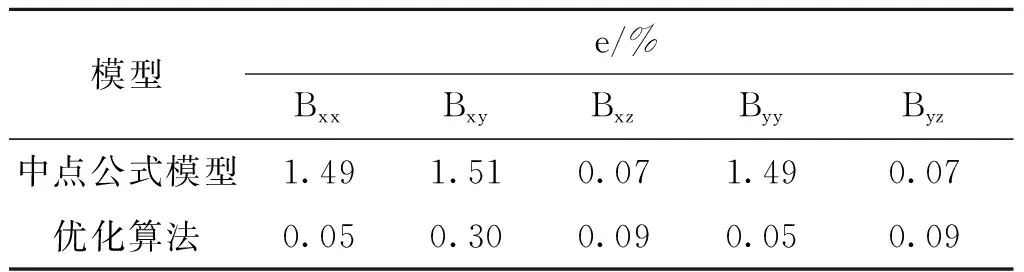
表2 优化模型与原模型的误差对比Tab.2 Error comparison of optimization model and original model

在表2中显然可以看出，相对于基于中点公式的原模型来说，5个磁场独立分量经过优化之后，误差明显减小，说明优化的结果是理想的。

4 结论

本文提出基于三点公式的直角四面体优化模型。该模型运用三点公式重新对直角四面体模型进行设计并提出新的梯度张量计算公式，两种结构进行对比分析，得出基于中点公式的直角四面体模型效果好的结论。在此基础上，基于免疫克隆算法对基于中点公式的直角四面体模型进行优化处理，再次提高对梯度张量的测量精度。仿真结果表明，本方法能充分利用磁场的三轴信息对磁场梯度张量进行测量，并能够提高磁梯度张量的测量精度。