新型四自由度3T1R并联机器人机构运动学分析与优化设计
2022-03-21彭红梅陈亚陆彩满刘艳梨吴洪涛
彭红梅,陈亚,陆彩满,刘艳梨,吴洪涛
新型四自由度3T1R并联机器人机构运动学分析与优化设计
彭红梅1,陈亚1,陆彩满1,刘艳梨2,吴洪涛2
(1.江苏安全技术职业学院 机械工程学院,江苏 徐州 221011;2.南京航空航天大学 机电学院,南京 210016)
针对自动化生产线分拣需求,提出一种新型四自由度的三平移一转动(3T1R)并联机器人机构。根据方位特征集设计理论验证并联机器人机构的运动性质。利用机构的构型特点建立运动学方程模型,对其进行位置正解和逆解的分析,通过数值法搜索得到并联机器人机构的工作空间图形和转动能力等高线图。同时分析并联机器人机构的雅可比矩阵X以及奇异性。最后以工作空间最大化作为适应度函数,基于遗传算法对机构结构尺寸进行最优化分析。该机构操作空间具有规则形状、无空洞、较大的特点,优化后的并联机器人机构工作空间性能提升45%。操作空间内运动灵活性较好,优化后工作空间性能得到显著改善。在电子包装自动化生产线搬运分拣领域具有较好的应用前景。
3T1R;并联机器人机构;方位特征集;工作空间;转动能力;奇异位形
三平移一转动(3T1R)并联机器人机构因其具有精度高、承载能力强、刚度大等诸多优点,广泛应用于分拣、包装及搬运等工程实际领域[1-2]。3T1R动并联机器人机构可通过改变动平台的姿态角使得工件姿态得以调整。在物料分拣、自动搬运、零件装配等应用场景中具有较好的应用前景[3-4]。
近年来3T1R并联机器人机构的分析与综合研究一直是学者们研究的重点。李宏伟等[5]以平行四边形机构构成的3TIR并联机器人机构为研究目标,介绍支链的构成和运动副的分布情况,根据理论方法计算机构自由度,与根据方位特征集计算得到的自由度结果完全一致。利用机构的运动特点建立运动学方程数学模型,完成运动学位置逆解计算,并提出一种确定工作空间准确的边界形状新型数值搜索法。该方法具有原理简单、搜索效率高、边界精度高等优点。此外,研究工作空间体积与结构参数尺寸的影响关系。GHAFFARI等[6]提出了一种3T1R并联机器人机构,该机构一般可用于涡轮叶片的加工,该机构具有部分解耦、结构简单、对称分布、控制容易的特点,并完成位置正解和位置逆解分析,并通过算例分析验证其正逆解可靠性,同时建立机构的动力学模型,并通过计算证明了机构在工作空间中不存在运动奇异的情况。利用几何方法对机构的工作空间进行了分析,得到了机构执行器在给定任务下所需的行程长度。沈惠平等[7]针对三平移一转动拓扑结构复杂所引起的新机型的研究和开发困难的问题,通过降低机构的耦合度来降低机构运动学分析难度,并通过具体案例分析降耦的全过程。畅博彦等[8]设计实现了整周回转运动的三平移一转动并联机器人机构,所提出的机构可通过平面二维移动放缩机构模块化装配,为了便于计算利用降耦设计原理对机构进行构型优化设计,以达到降低耦合度但不改变运动性质的效果。建立运动方程计算位置正逆解,图形化分析工作空间和转动能力,并通过讨论奇异性出现的可能情况,以此来指导开发人员调整设计参数避免这类问题出现,并讨论参数变化对操作空间影响趋势,分析机构执行末端的转动最大角度得到转动能力图谱。
受文献[9]启发,设计一种新型的3T1R并联机器人机构,它具有空间三平移和绕着轴转动的运动特点,机构的结构类型为2PRPU,即每条支链由2条完全相同的PRPU支链构成,基于方位特征集设计理论验证构型为2PRPU的3T1R并联机器人机构性质,并建立3T1R并联机器人机构的运动学模型。以一组算例详细分析并联机器人机构的操作空间指标,研究不同高度下对转动能力的影响,最后以实际性能需求为目标模型对该机构进行参数的优化设计。
1 并联机器人机构简介
1.1 机构模型
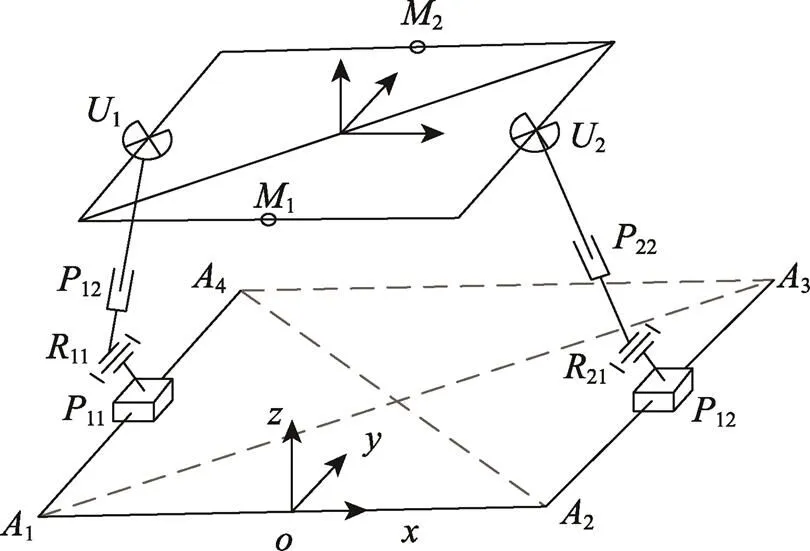
图1 3T1R并联机器人机构的结构
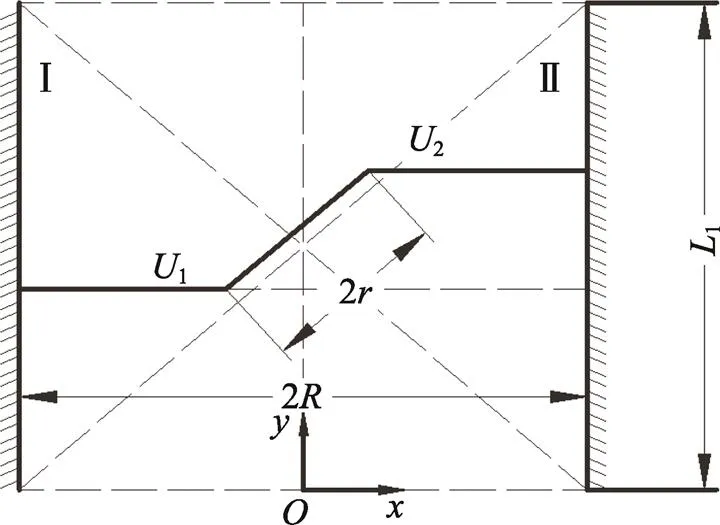
图2 xOy面投影的结构简图
1.2 机构的拓扑特性分析
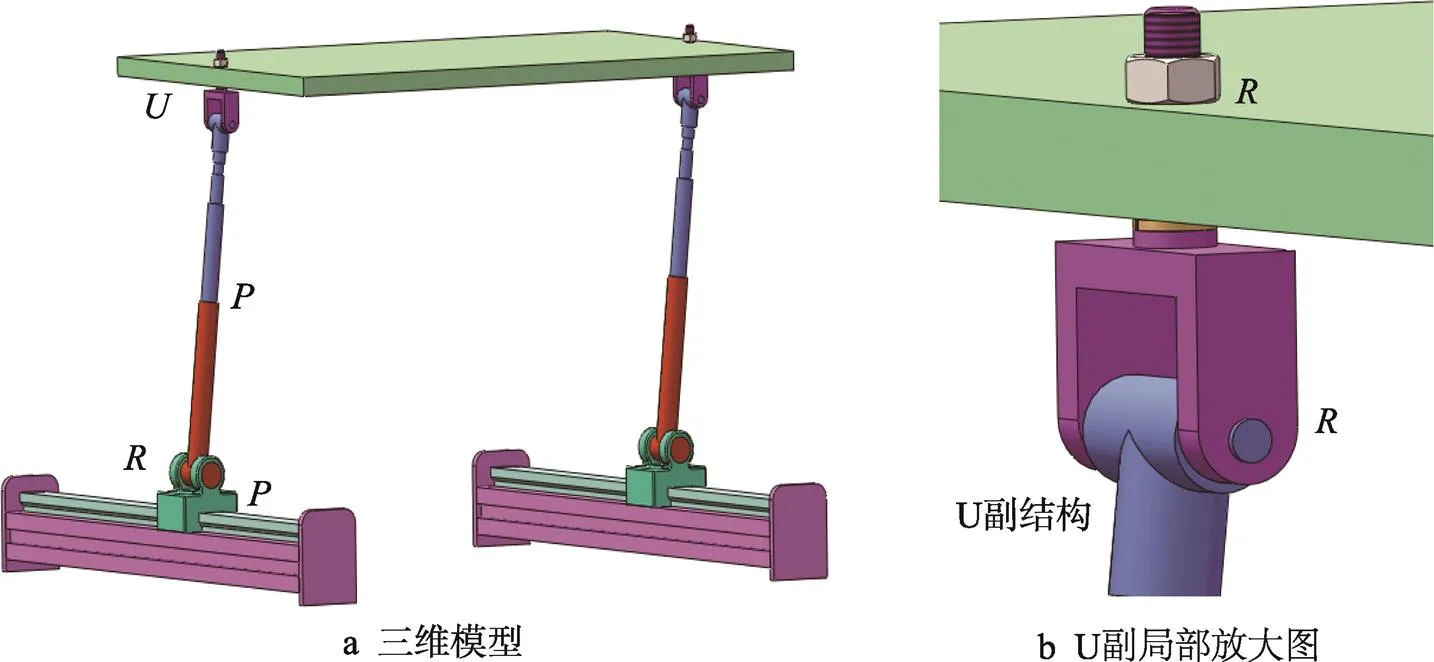
图3 3T1R并联机器人机构的三维模型
(1)
1)通过支链的方位特征集,将支链1、2设置为一个独立运动回路,计算得到的位移方程数:
(2)
2)分析构型为2PRPU的3T1R并联机器人机构动平台参考点的POC集:
Pa(1-2)=b1b1=
(3)
3)自由度计算为:
(4)
4)机构的耦合度是评价机构运动控制难易程度的特性参数,耦合度越高,机构控制越难实现,耦合度分析需要根据支链的约束度来计算,已知主动副的数目为4,分析得到SOC的约束度:
0 (5)
(6)
综上所述的拓扑结构特性分析,验证3T1R并联机器人机构具有空间、、方向移动,且沿着动平台轴线转动的特性。另外,耦合度=0说明机构具有解耦性,控制运动易实现,位置分析不复杂。不需要通过数值搜索法来计算正解,可直接推导得到正解解析式。
2 位置分析
2.1 位置正解分析
OP(7)
(8)
根据式(8)推导出位置正解见式(9)。
(9)
根据式(9)分析表明,构型为2PRPU的3T1R并联机器人机构的位置正解并不复杂,结果清晰简单,且整个计算过程容易,根据输入位移能得到4组执行末端位姿解。
2.2 位置逆解分析
(10)
3 奇异分析
3.1 机构雅克比矩阵
(11)
3.2 逆解奇异性分析
3.3 正解奇异性分析
4 工作空间分析
工作空间形状可能直接影响机构应用范围[10]。当机构的操作空间内部不连续时,会使得应用受到极大约束限制,因此研究机构时,分析工作空间尤为关键。
4.1 可达工作空间分析
极限搜索法搜索并联机器人机构的工作空间需要根据建立的运动方程模型进行求解,下面选择尺寸参数分析并联机器人机构工作空间,具体参数值见表1。
表1 算例的结构参数值

Tab.1 Structural parameters of an example
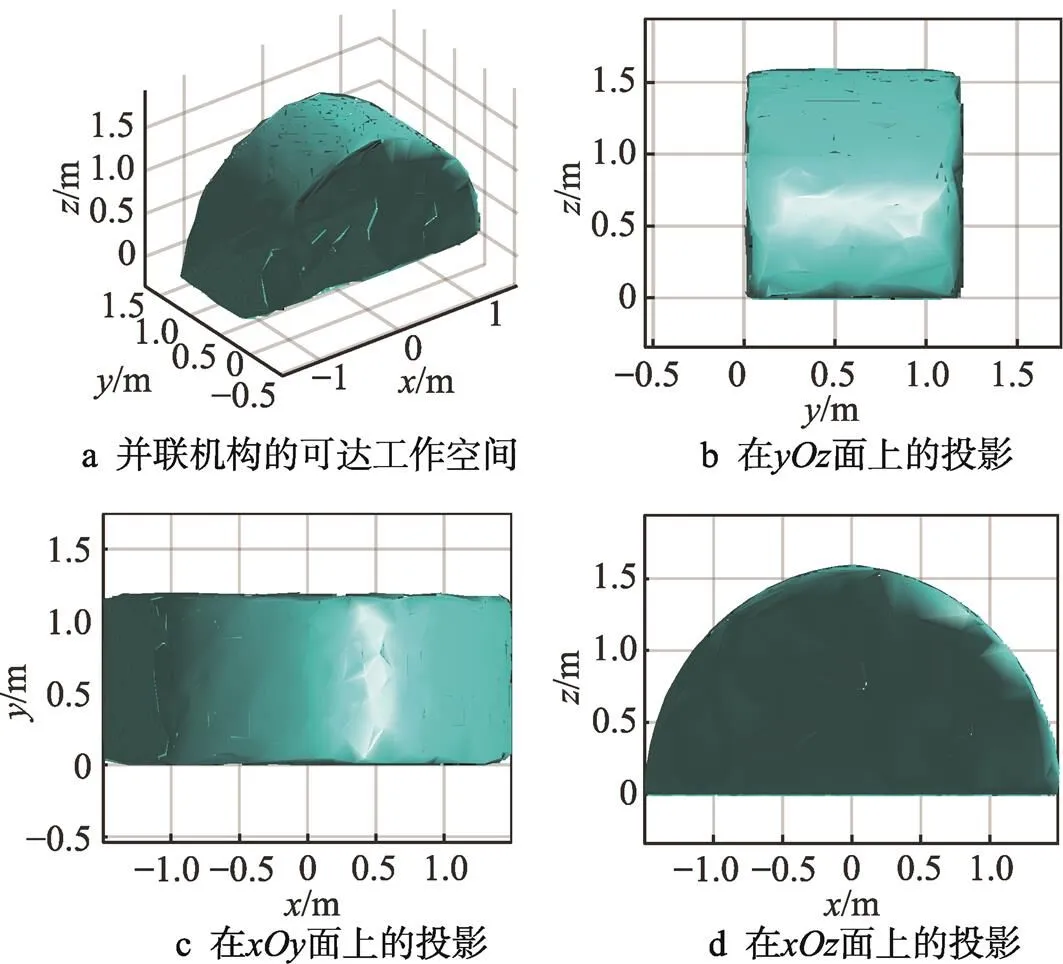
图4 3T1R机构可达工作空间图
由图4分析可得,可达工作空间形状是对称图形,沿着每个投影面的图形是规则的,边界光滑饱满且内部无空洞的情况。工作空间三维图沿着投影面边界形状为长方形,且沿着=0对称分布;沿着投影面边界形状也是长方形,且沿着=0对称分布。沿着投影面边界呈对称的半椭圆形状,且沿着=0对称分布。该并联机器人机构整体的运动范围相对较大,可满足高速轻载自动化生产线搬运分拣作业需求,可应用于电子包装、食品医药、现代物流分拣等领域。
4.2 定姿态工作空间分析
不同姿态角的定姿态工作空间大小和形状存在差异[11]。分析姿态角为30°、60°、90°下的定姿态工作空间见图5—7。
由图5—7对比分析可得,3种定姿态(30°、60°、90°)工作空间三维图基本相同,姿态角对工作空间投影面影响比较大,对轴方向几乎没影响。2种工作空间的形状基本相同,仅大小上存在差异。姿态角对工作空间形状的影响不够显著。
5 并联机器人机构转动能力分析
由于3T1R并联机器人机构具有三平移一转动的运动特性,动平台可沿着轴转动,转动能力也是衡量3T1R并联机器人机构性能优劣的重要评价指标。转动能力指工作空间内动平台执行末端转动的最大范围[12],因此,研究转动能力对指导设计并联机器人机构的开发极其重要[13]。为了简化计算,通过分析不同高度下所对应截面的下可达工作空间内动平台执行末端转动的范围。分别取0、0.5、1、1.3等高度,对比分析操作空间内的并联机器人机构的转动能力。不同截面()下,转动能力等高线图见图8。
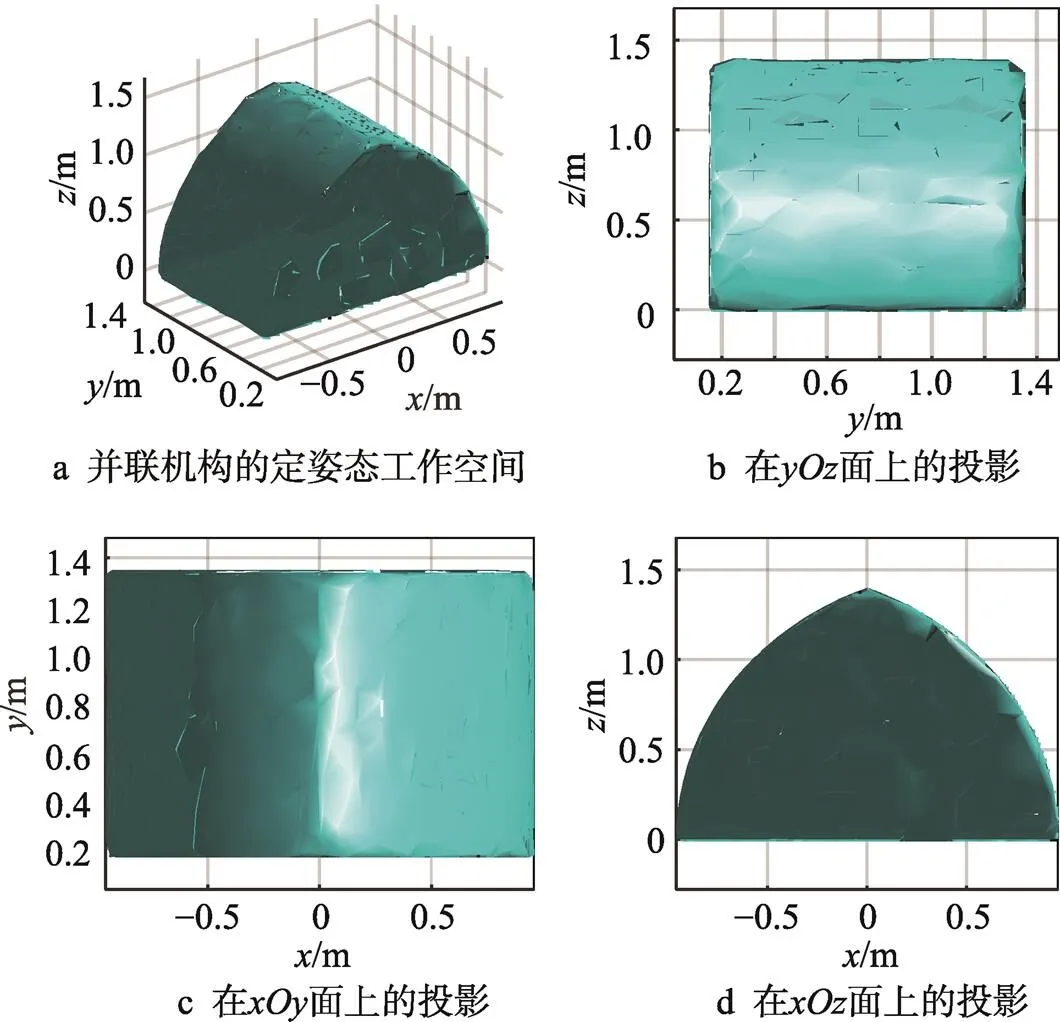
图5 姿态角q=30°时的定姿态工作空间
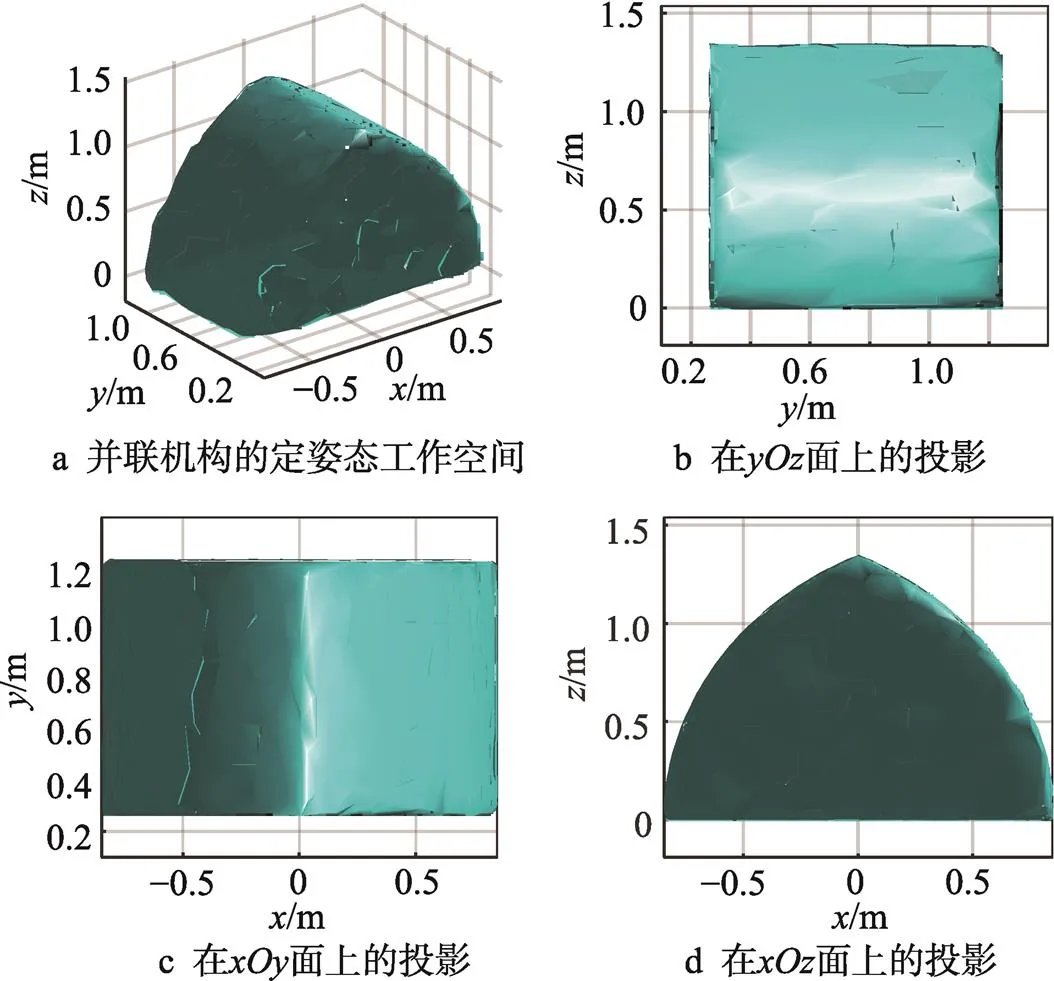
图6 姿态角q=60°时的定姿态工作空间
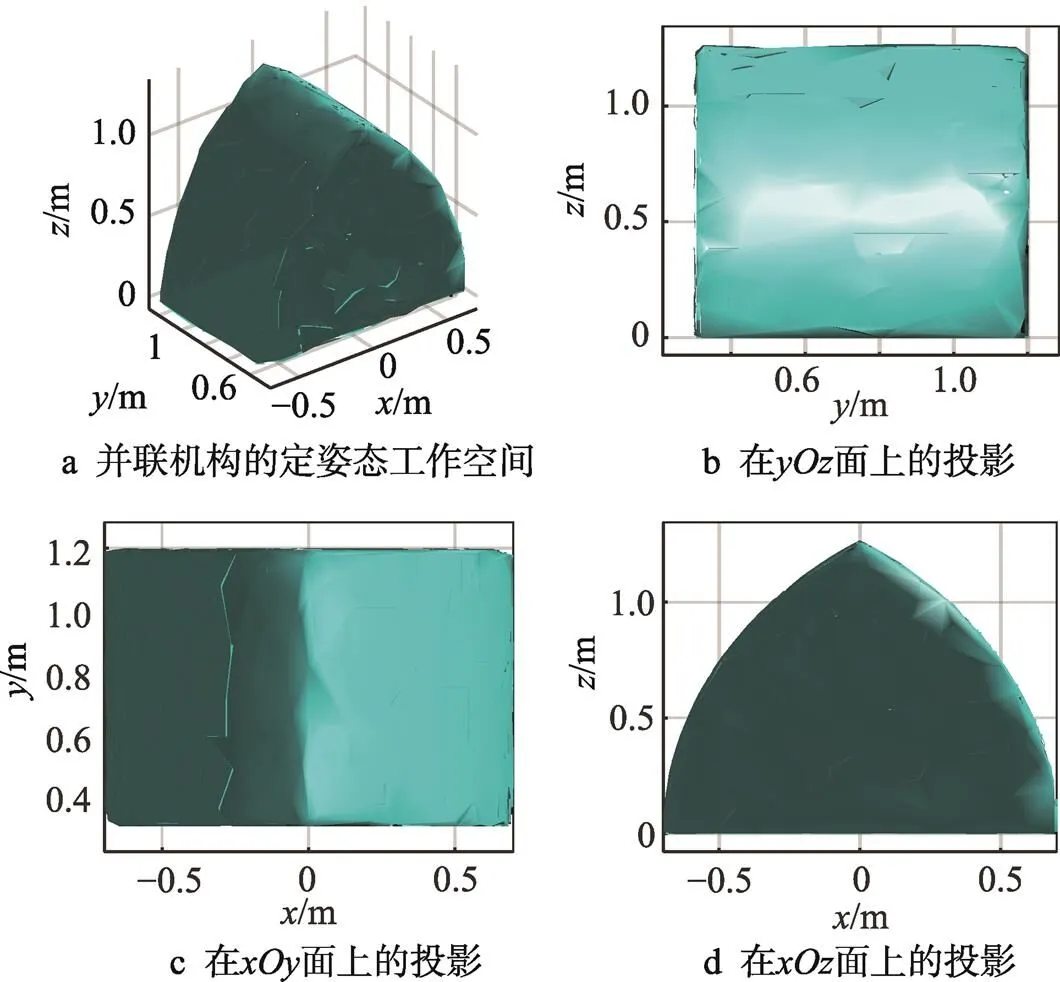
图7 姿态角q=90°时的定姿态工作空间
6 结构参数优化
6.1 模型优化的建立和算法选择
参数优化指在结构参数的范围内,通过优化方法搜索得到一组最佳工作性能最优化参数值,因此,以可达工作空间大小作为优化目标模型,分别对动、静平台的半径、,移动副最大移动距离,移动副最大移动距离等参数优化。优化过程是指给定、、、的范围,搜索出满足优化函数的最优解。参数优化范围选择参考文献[14],适应度函数优化模型为:
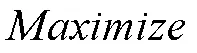
条件
文中选择模拟自然进化过程搜索遗传算法进行参数最优化设计[15],算法选择的参数进化代数为40,种群大小为40,适应度计算采用排序法,选择随机遍历抽样算法,重组方式选择分散重组,交叉概率为0.6,变异概率为0.008。
6.2 优化算例
根据6.1节提出的目标函数模型对其进行仿真优化,通过Matlab软件得到优化仿真图见图9—10。
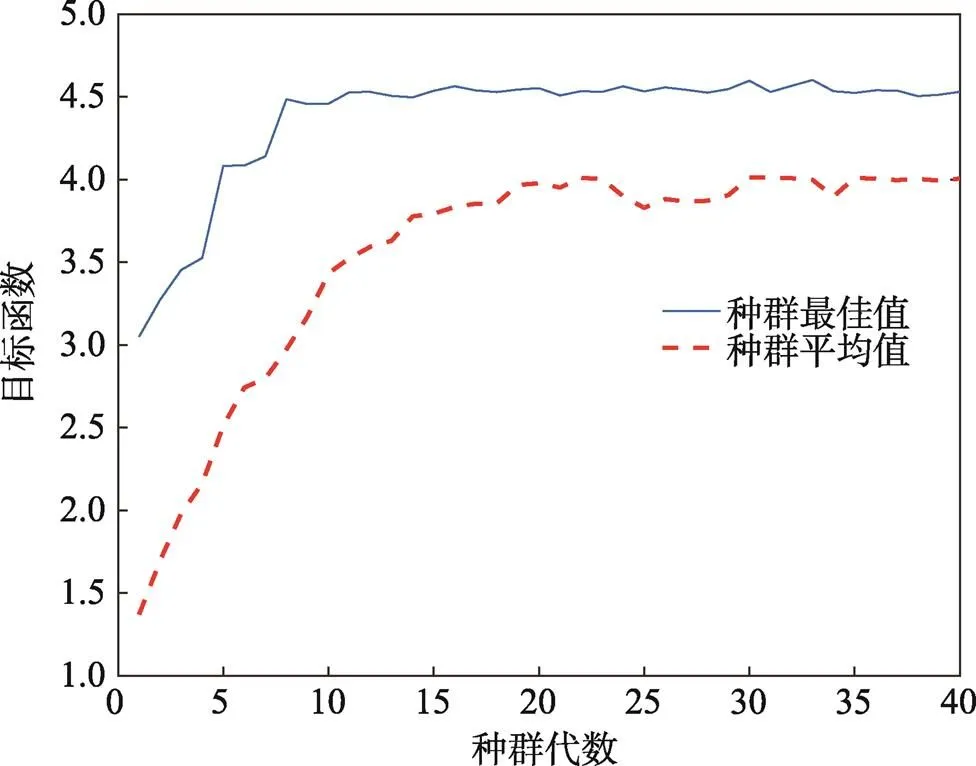
图9 最佳目标函数变化曲线
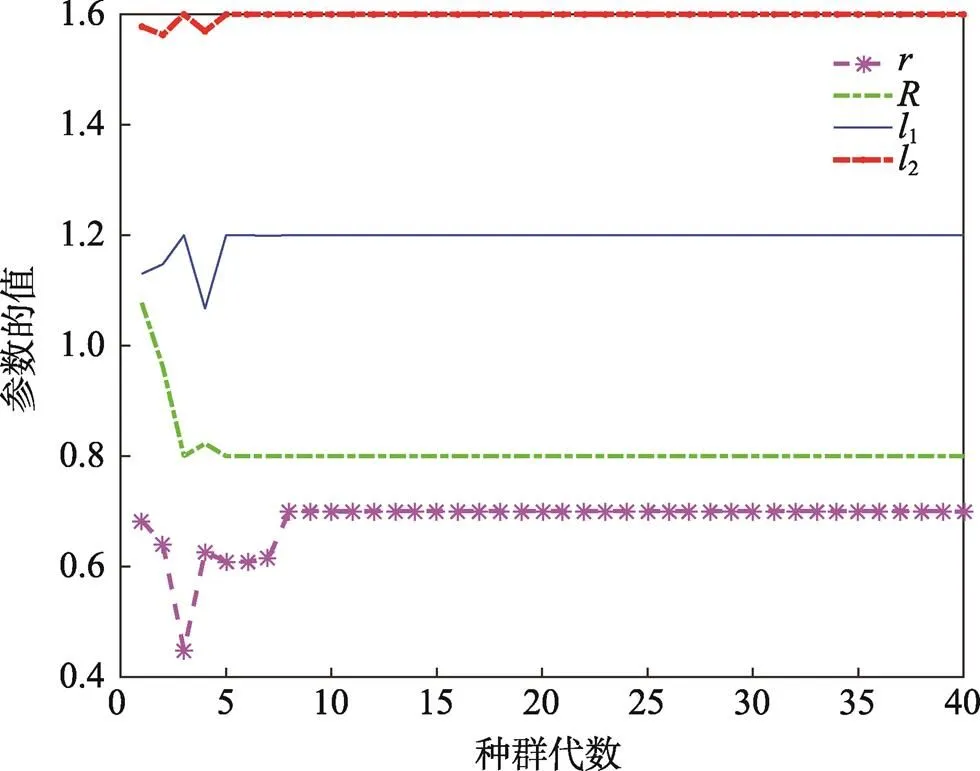
图10 设计参数变化曲线
由图9—10分析可得,迭代次数为15左右时已经得到最优目标=4.5m3。最优化对应的尺寸的参数、、、1、2分别为0.7、0.8、1.2、1.6 m。
根据优化后的参数值得到此参数下的三维图,进行对比分析,优化后的可达工作空间见图11。对比分析表明,优化后边界形状光滑丰满、对称分布。较优化前工作空间(=3.09 m3)大;优化后操作性能改善显著,较优化前的性能提升45%。
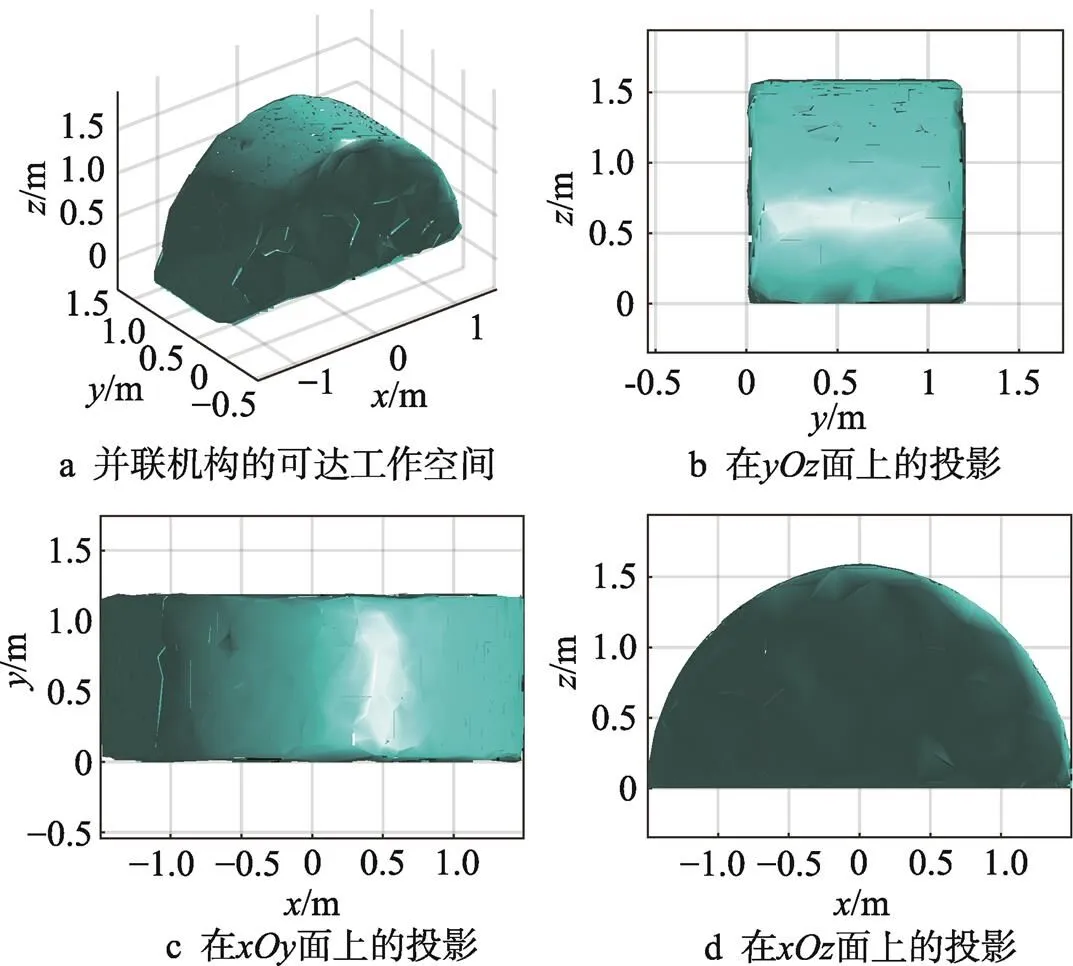
图11 优化后的工作空间
7 结语
1)设计一种构型为2PRPU的3T1R并联机器人机构,根据方位特征方程的理论推导出机构具有空间三维移动且沿着轴的运动性质。
2)完成位置正解和逆解分析。结果表明,并联机器人机构最多存在4组正解和4组逆解。
4)算例分析机构得到较好的工作空间性能,工作空间形状对称分布,内部无空洞情况,临界位置光滑饱满。另外,分别计算为0、0.5、1、1.3等高度下的转动能力。分析表明,随着越大,所对应的转动能力逐渐减小。
[1] 洪俊坤, 车林仙, 杜力, 等. 2-(CRR)2R结构降耦并联机构及其运动学分析[J]. 机械传动, 2019, 43(4): 51-60.
HONG Jun-kun, CHE Lin-xian, DU Li, et al. 2-(CRR) 2R Parallel Mechanism with Decoupling-Reducing Structure and Its Kinematics Analysis[J]. Journal of Mechanical Transmission, 2019, 43(4): 51-60.
[2] 沈惠平, 张震, 杨廷力, 等. 3T1R并联机构结构降耦设计与运动学分析[J]. 农业机械学报, 2017, 48(10): 380-389.
SHEN Hui-ping, ZHANG Zhen, YANG Ting-li, et al. Structure Coupling-Reducing Design and Kinematics Analysis of 3T1R Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(10): 380-389.
[3] ZHANG Xing, YANG Ming-xing, MU De-jun, et al. Unified Formulas of Constrained Jacobian and Hessian Matrices for 3T1R Overconstrained Parallel Mechanisms[J]. Mechanics Based Design of Structures and Machines, 2021, 1: 1-15.
[4] BRIOT S, BONEV I A. a New 3T1R Decoupled Parallel Manipulator for Pick-and-Place Applications[J]. Mechanism & Machine Theory, 2010, 45(5): 707-721.
[5] 李宏伟. 4自由度3T1R并联机构工作空间与转动能力分析[J]. 机械设计与研究, 2020, 36(5): 75-80.
LI Hong-wei. Workspace and Rotation Capacity Analysis of 4-DOF 3T1R Parallel Mechanism[J]. Machine Design & Research, 2020, 36(5): 75-80.
[6] GHAFFARI H, PAYEGANEH G, ARBABTAFTI M. Kinematic Design of a Novel 4-DOF Parallel Mechanism for Turbine Blade Machining[J]. The International Journal of Advanced Manufacturing Technology, 2014, 74(5-8): 729-739.
[7] 沈惠平, 强恒存, 曾氢菲, 等. 基于结构降耦的一类低耦合度新型3T1R并联机构的拓扑设计[J]. 中国机械工程, 2017, 28(10): 1163-1171.
SHEN Hui-ping, QIANG Heng-cun, ZENG Qing-fei, et al. Topological Design for a Class of Novel 3T1R Parallel Mechanisms with Low Coupling Degree Based on Coupling-Reducing[J]. China Mechanical Engineering, 2017, 28(10): 1163-1171.
[8] 畅博彦, 李晓宁, 金国光, 等. 具有整周回转能力的3T1R并联机构运动学分析[J]. 农业机械学报, 2019, 50(7): 406-416.
CHANG Bo-yan, LI Xiao-ning, JIN Guo-guang, et al. Kinematics Analysis of Novel 3T1R Parallel Manipulator with Full Rotational Capability[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(7): 406-416.
[9] 吴存存, 杨桂林, 陈庆盈, 等. 四自由度2PPPaR并联机构运动学及性能分析[J]. 机械工程学报, 2018, 54(3): 36-45.
WU Cun-cun, YANG Gui-lin, CHEN Qing-ying, et al. Kinematic and Performance Analysis of a 4-DOF 2PPPaR Parallel Manipulator[J]. Journal of Mechanical Engineering, 2018, 54(3): 36-45.
[10] 崔马茹, 武建德, 李瑞琴, 等. 3-URPR并联机构的逆运动学与可达工作空间分析[J]. 包装工程, 2020, 41(21): 196-201.
CUI Ma-ru, WU Jian-de, LI Rui-qin, et al. Inverse Kinematics and Reachable Workspace of 3-URPR Parallel Mechanism[J]. Packaging Engineering, 2020, 41(21): 196-201.
[11] 马振东, 马春生, 米文博, 等. 基于2-RPS/UPRS并联机构的自动分拣机运动分析[J]. 包装工程, 2021, 42(1): 157-162.
MA Zhen-dong, MA Chun-sheng, MI Wen-bo, et al. Kinematics Analysis of Automatic Sorter Based on 2-RPS/UPRS Parallel Mechanism[J]. Packaging Engineering, 2021, 42(1): 157-162.
[12] 沈惠平, 许正骁, 许可, 等. 低耦合度且部分解耦的3T1R并联机构设计与分析[J]. 农业机械学报, 2019(2): 373-383.
SHEN Hui-ping, XU Zheng-xiao, XU Ke, et al. Design and Analysis for Partially Decoupled 3T1R Parallel Mechanism with Low Coupling Degree[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019(2): 373-383.
[13] 刘勇, 许勇, 宋伟, 等. 对称3T1R并联机构构型设计与位置分析[J]. 机械设计与研究, 2019, 35(2): 55-59.
LIU Yong, XU Yong, SONG Wei, et al. Configuration Design and Position Analysis of Symmetrical 3T1R Parallel Mechanisms[J]. Machine Design & Research, 2019, 35(2): 55-59.
[14] 李旭, 罗霞, 罗成, 等. 基于离散蒙特卡洛的一种3T1R并联机构工作空间分析[J]. 机械, 2020, 47(5): 27-32.
LI Xu, LUO Xia, LUO Cheng, et al. A Discrete Monte Carlo Approach to Workspace Analysis of a Type of 3T1R Parallel Mechanism[J]. Machinery, 2020, 47(5): 27-32.
[15] 李伟, 何鹏举, 杨恒, 等. 基于粗糙集和改进遗传算法优化BP神经网络的算法研究[J]. 西北工业大学学报, 2012, 30(4): 601-606.
LI Wei, HE Peng-ju, YANG Heng, et al. An Effective Backpropagation Algorithm for Optimizing BP Neural Network Based on Rough Set and Modified Genetic Algorithm[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 601-606.
Kinematics Analysis and Optimization Design of a New Four Degree of Freedom 3T1R Parallel Robot Mechanism
PENG Hong-mei1, CHEN Ya1, LU Cai-man1, LIU Yan-li2, WU Hong-tao2
(1.Department of Mechanical Engineering, Jiangsu College of Safety Technology, Xuzhou 221011, China; 2.School of Electrical and Mechanical, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The work aims to propose a novel 4-DOF 3-translational-1-rotational (3T1R) parallel robot mechanism to meet the needs of sorting in automatic production line. The kinematic properties of the parallel mechanism were verified according to the design theory of orientation feature set. Based on the configuration characteristics of the mechanism, the kinematics equation model was established, and the forward and inverse position solutions of the mechanism were analyzed. The workspace figure and rotation capacity contour map of the parallel mechanism were obtained by numerical method. At the same time, the Jacobian matrixXand singularity of the parallel mechanism were analyzed. Finally, with the maximum workspace as the fitness function, the structure size of the mechanism was optimized based on genetic algorithm. The operating space of the mechanism had the characteristics of regular shape, no cavity, large size, and good motion flexibility in the operating space. The workspace performance of the optimized parallel mechanism was increased by 45%. The kinematic dexterity in the workspace is good. The performance of the workspace is significantly improved after optimization. It has a good application prospect in the field of electronic packaging automatic production line handling and sorting.
3T1R; parallel mechanism; position and orientation characteristics; workspace; rotation ability; singularity
TB486;TH122
A
1001-3563(2022)05-0188-08
10.19554/j.cnki.1001-3563.2022.05.026
2021-06-10
国家自然科学基金(51975277)
彭红梅(1977—),女,江苏安全技术职业学院讲师,主要研究方向为机械自动化、机械优化设计。
