金属橡胶减振器抗冲击特性有限元仿真研究
2022-03-21鲍继轩原霞薛双桥徐少男马艺霖王钊晖
鲍继轩,原霞,薛双桥,徐少男,马艺霖,王钊晖
缓冲与隔振
金属橡胶减振器抗冲击特性有限元仿真研究
鲍继轩,原霞,薛双桥,徐少男,马艺霖,王钊晖
(中北大学 机械工程学院,太原 030051)
提出一种用于工程计算的金属橡胶数值模拟方法,为制备缓冲性能良好的金属橡胶材料提供了理论基础。建立金属橡胶减振器有限元模型,由Sprng-Dampr165单元定义金属橡胶材料;通过数值模拟,计算了不同负载质量对其抗冲击特性的影响,并对其进行可行性分析。有限元结果表明,响应加速度峰值在负载质量为4.2 kg时,最大误差为27.72%;在负载质量为9.8 kg时,最大误差为38.15%,试验结果与有限元结果趋势相同,验证了其可行性。当冲击载荷较小时,提出的数值模拟方法在模拟金属橡胶减振器的抗冲击特性时有着较好的表现。
金属橡胶;非线性刚度;抗冲击特性;弹簧阻尼单元
金属橡胶材料是一种经过螺旋卷绕制、毛坯缠绕、冷冲压成型的新型结构阻尼材料,由于其既有橡胶的阻尼特性,又有金属材料的耐高温、抗腐蚀、抗冲击特性,因而又被称为金属橡胶材料[1-4]。迄今为止,国内外学者对建立金属橡胶本构模型做了大量研究。侯军伟等[5]提出了金属橡胶简支梁本构模型。邵晓宙等[6]提出了一种金属橡胶M-R修正模型,适用于数值模拟。闫辉等[7-9]对金属橡胶减振系统进行了宽带随机振动试验和冲击试验。马艳红等[10-13]推导了不同结构参数的金属橡胶刚度和阻尼的表达式。唱忠良等[14]进行了金属橡胶减振器冲击加速度响应最大值的理论推导。在工程实际中,构件损坏往往是由冲击载荷引起的。目前为止,对于冲击问题的研究仍集中在试验和理论研究上。综上所述,抗冲击有限元仿真研究对优化减振器的设计具有重要指导意义。
文中提出一种由Sprng-Dampr165单元定义金属橡胶材料的数值模拟方法,对一军用装甲车减振器进行冲击数值模拟,并与试验数据对比,测试此方法的可靠性,并为新型金属橡胶减振器的研发提供理论依据。
1 金属橡胶减振器静态和冲击试验
1.1 静态压缩试验
装甲车某型号金属橡胶减振器见图1,该减振器主要包括端盖、底座、连接轴和2块金属橡胶缓冲垫。2块金属橡胶缓冲垫交替作用,起到缓冲保护的作用,端盖与底座依靠连接轴相连接。
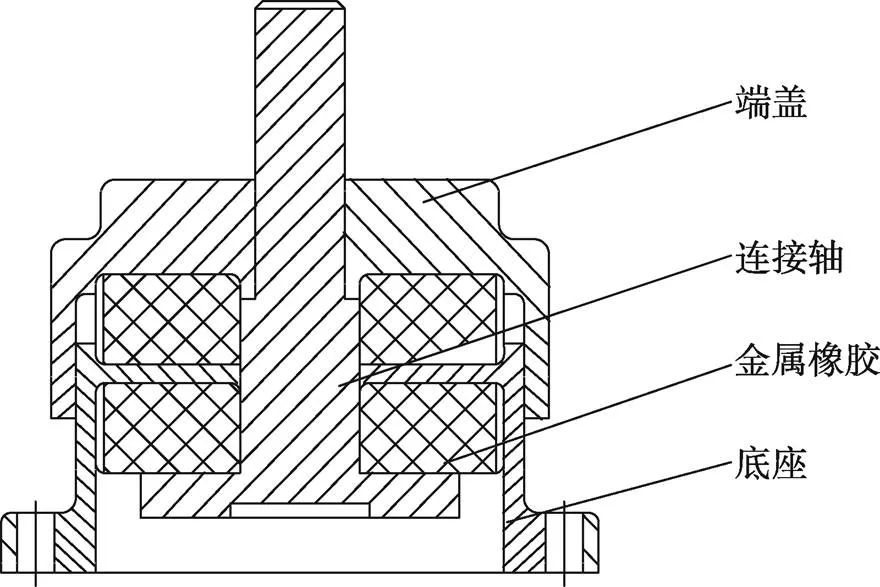
图1 金属橡胶减振器结构
对相对密度为0.20、0.25和0.30的金属橡胶减振器(预紧量为20%)进行准静态压缩试验,得到有限元模型所需的仿真参数,见图2。静态压缩试验见图3。
1.2 冲击试验
试验使用的冲击试验装置是苏州苏试试验仪器DC-10000-100型号的电动式振动台,该试验机由振动控制仪、冲击台体、加速度计等装置组成,见图4。
试验开始前,振动控制系统将已经由计算机设定的参数转化为冲击加速度激励,具体步骤如下:首先振动控制系统使冲击台面上升到指定位置,随之台面自由下落,与底座上的波形发生器碰撞,产生符合要求的半正弦激励。上下2个加速度传感器分别将采集来的冲击台面上的冲击激励,以及由减振器振动传递后配重上的响应加速度信号发送到数据采集系统,便于在计算机上观察和处理,试验场景见图。

图2 不同相对密度的准静态压缩曲线

图3 准静态压缩试验
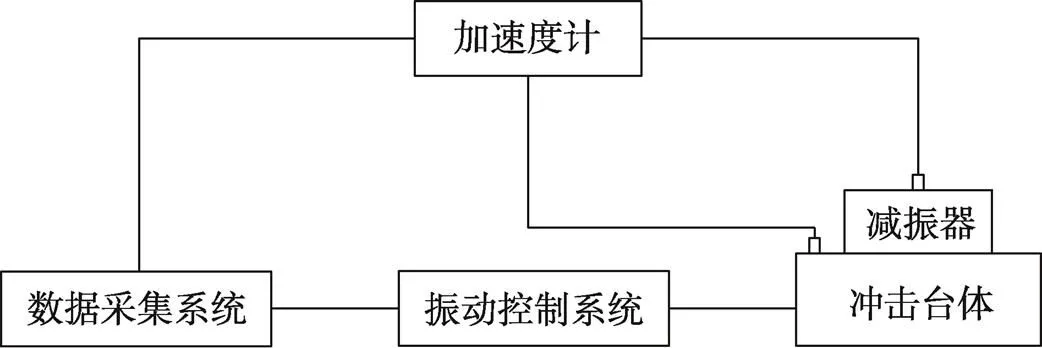
图4 冲击试验原理

图5 冲击试验
对试件参数与准静态压缩试验相同的金属橡胶减振器进行冲击试验,分别安装质量为4.2 kg和9.8 kg的配重,采用特定的波形发生器,使其产生脉冲宽度为6 ms的半正弦加速度脉冲激励,见图6。
由图7可以看出,跌落高度和负载质量与加速度响应峰值成正比,与加速度响应衰减速率成反比,因为金属橡胶材料刚度的大小受到其位移变形量的 影响[15]。
2 金属橡胶减振器冲击仿真
2.1 仿真模型的建立
以1.1节提到的金属橡胶减振器为基础,用Ansys Workbench建立相应的有限元模型,并与试验施加相同的加速度激励,在减振器缓冲作用下,激励传递至配重质量块。
以图8中的仿真原理模型为依据,建立等效模型,对其进行网格划分见图9,其中底座、端盖和连接轴材料为铝合金,负载质量采用钢板制成,材料参数见表1。4个非线性弹簧单元和4个阻尼单元对称分布在端盖与底座,底座与连接轴之间,对并联的弹簧单元的弹簧刚度和阻尼单元的阻尼系数进行叠加,计算单个弹簧阻尼单元的弹簧刚度及阻尼系数。接下来,对模型中的所有节点在和方向上的运动自由度进行约束,对底座的底面施加冲击激励,方向竖直向上,施加效果见图10。
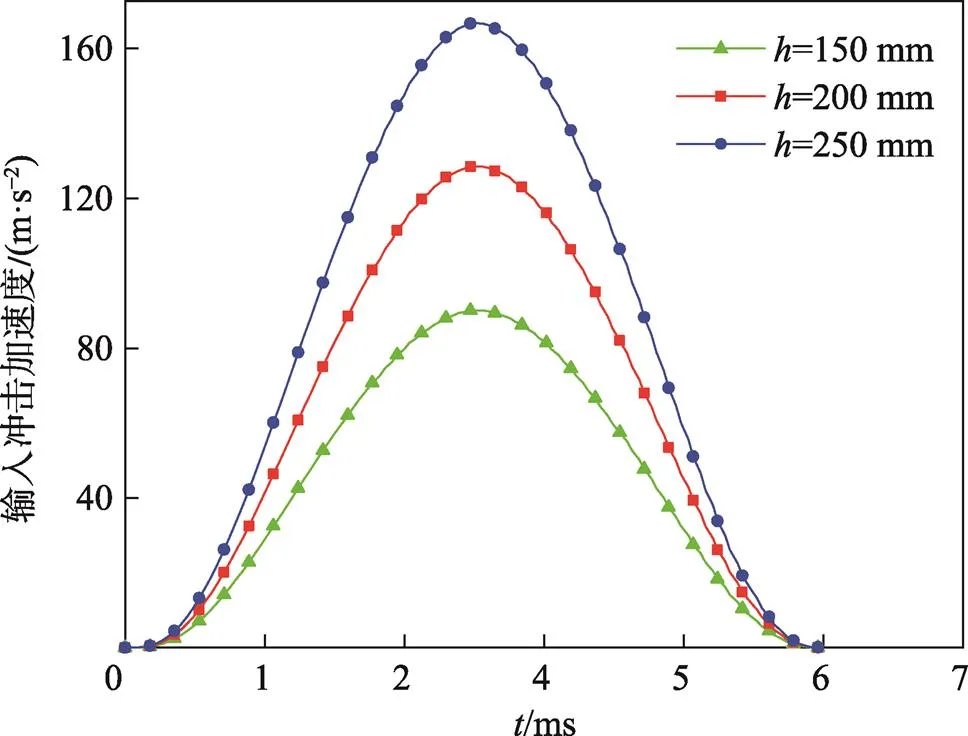
图6 不同跌落高度的加速度激励
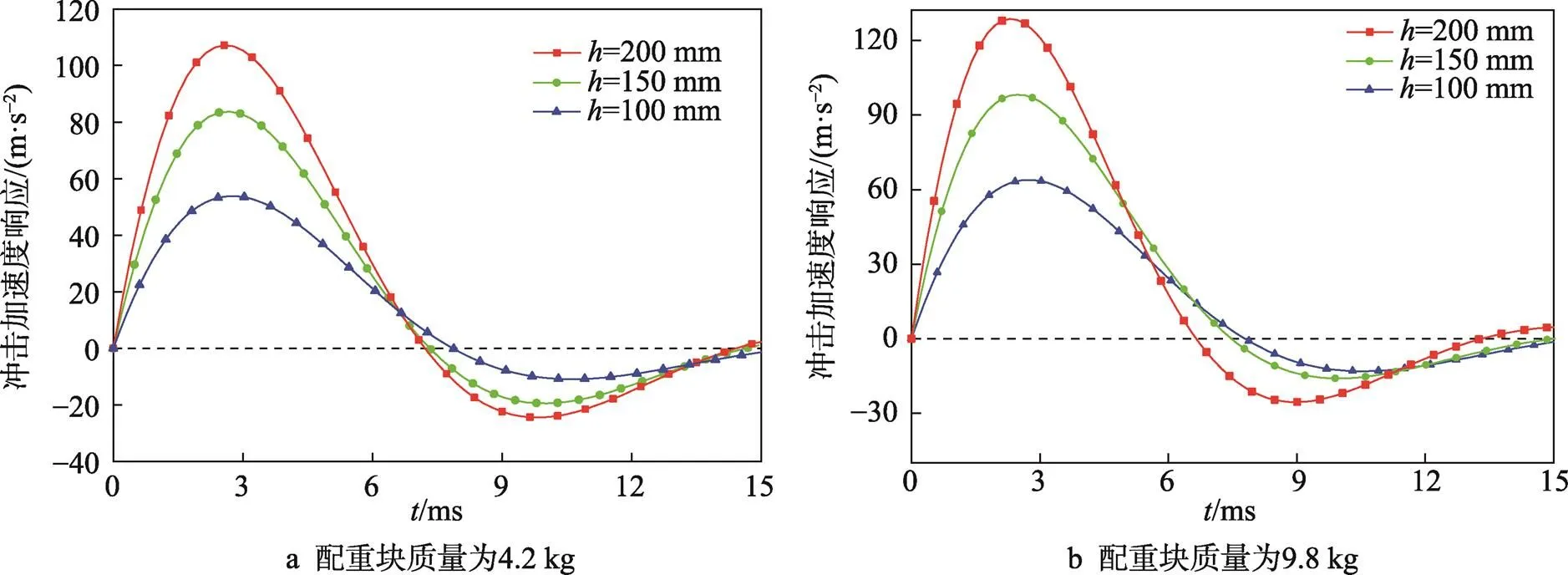
图7 冲击试验结果
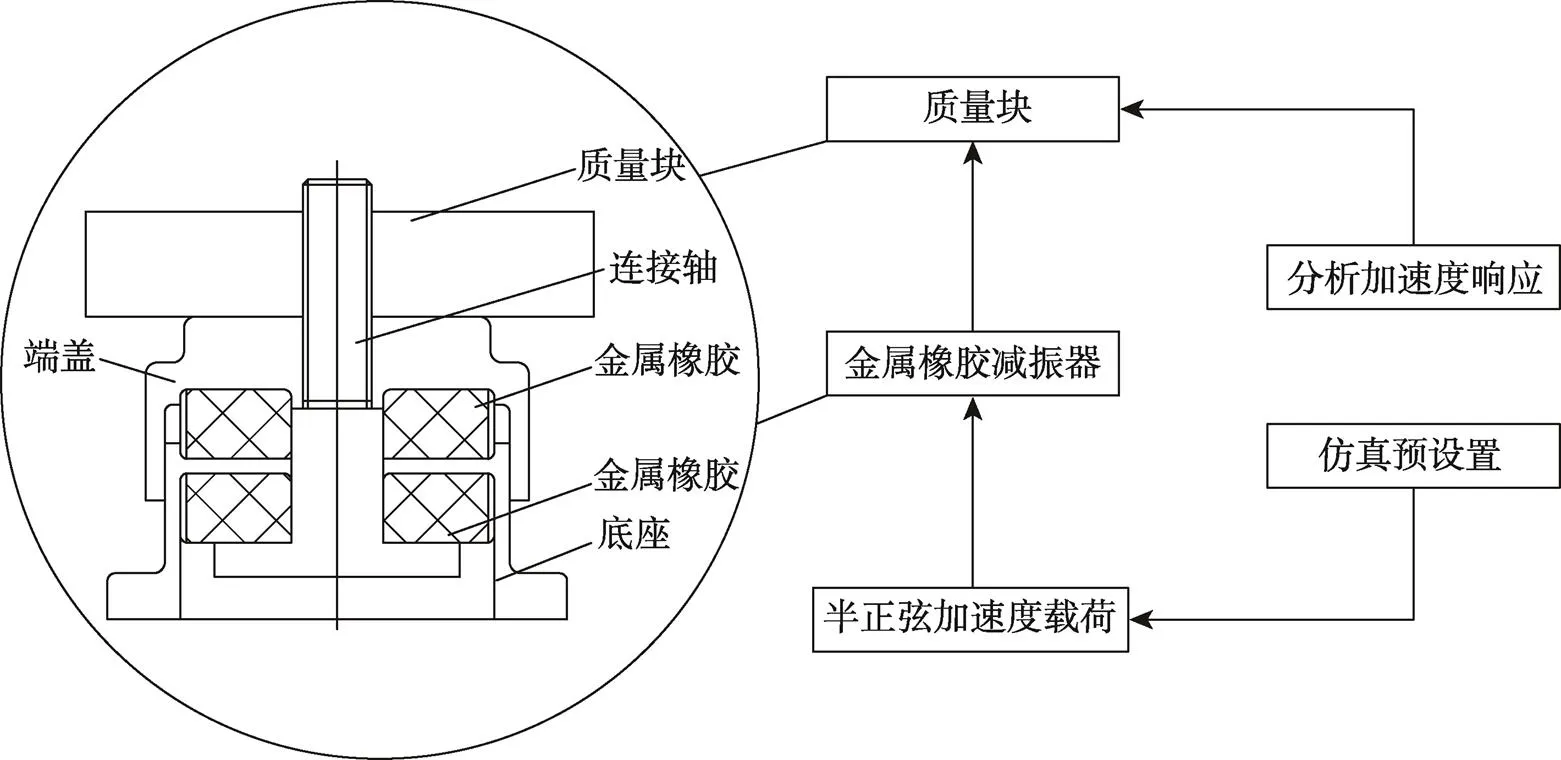
图8 抗冲击仿真原理
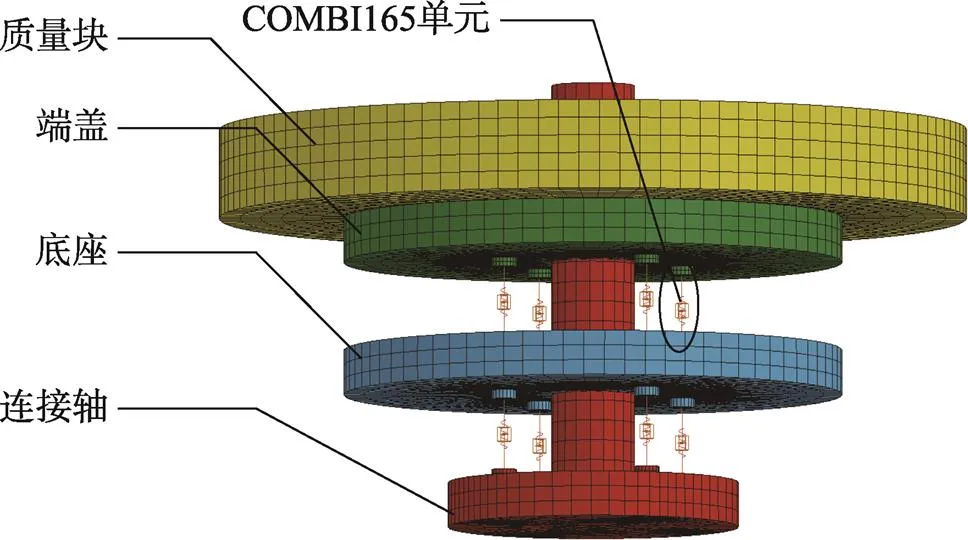
图9 有限元模型
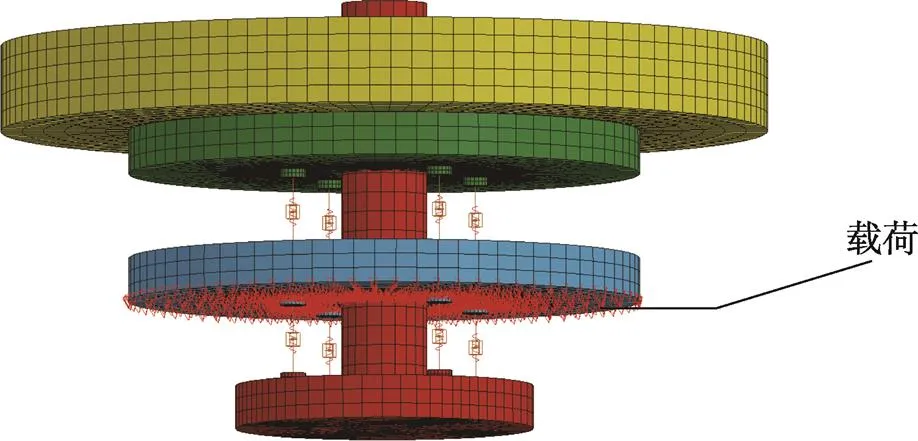
图10 载荷施加
表1 材料参数

Tab.1 Material parameters
2.2 弹簧阻尼单元冲击仿真参数识别
Sprng-Dampr165单元包括非线性弹簧单元和阻尼单元,将金属橡胶试件的冲击特性本构曲线经过处理导入到弹簧单元中,金属橡胶材料属性的定义问题得到解决。图1所示的金属橡胶减振器,因为连接轴与端盖螺纹连接,则减振器无论受到拉伸载荷还是压缩载荷,2个减振元件总是一个处于卸载状态,另一个处于加载状态,因此,模拟上、下2个减振元件时,采用对称分布互为并联的2层弹簧单元(每层4个),2种工作状态下的减振元件的刚度叠加决定了金属橡胶减振器的刚度。设减振元件的刚度为(),为减振元件的位移变形量,则金属橡胶减振器的总刚度为:
(1)
单个弹簧单元的非线性刚度为:
(2)
根据实际工况确定金属橡胶减振器的缓冲元件位移变形量为4 mm。对相对密度为0.20的金属橡胶试件的非线性刚度进行分段化处理,见图11,考虑到减振器的平衡位置,根据式(2)弹簧单元的非线性刚度,将其起点平移至原点。如图12所示,对其积分即可定义金属橡胶材料的非线性刚度,见图13。

图11 分段式非线性刚度
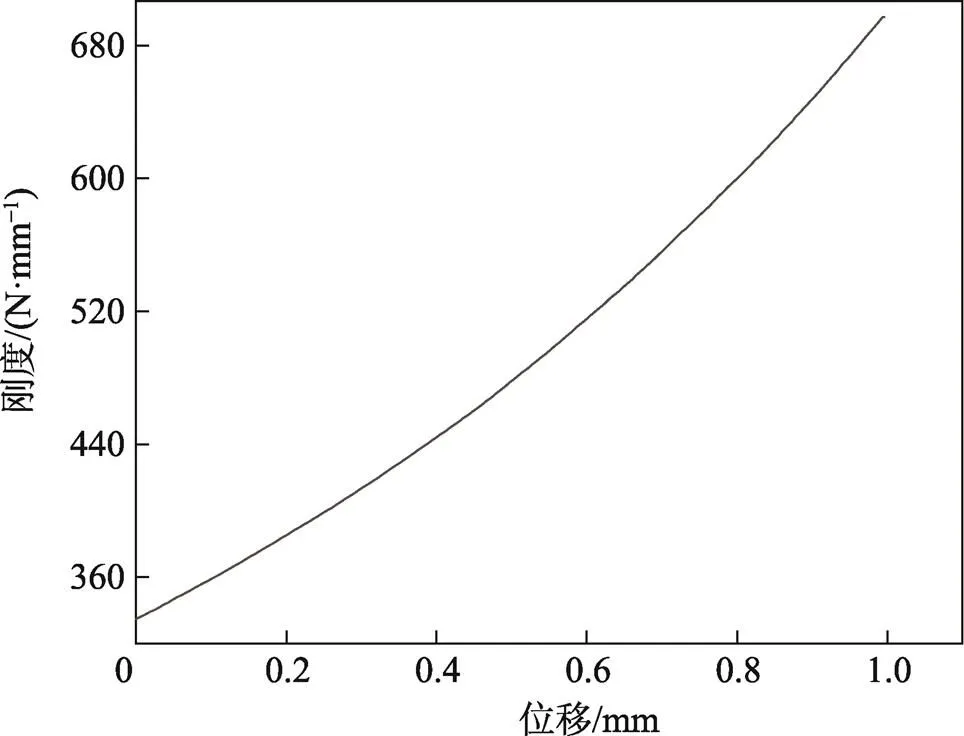
图12 叠加后的非线性刚度
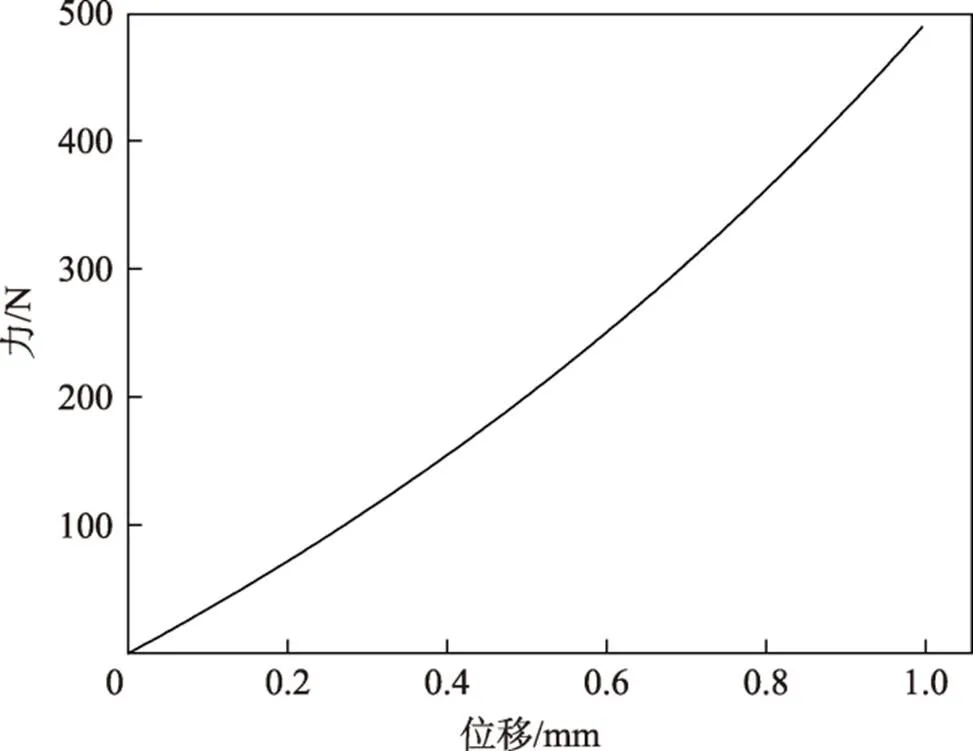
图13 有限元模型输入力-位移曲线
SPRNG-DAMPR165单元通过常阻尼系数定义金属橡胶材料的阻尼,其公式为:
(3)
2.3 仿真结果分析
2.3.1 试验结果与仿真结果对比分析
从图14可以看出,Sprng-Dampr165单元模拟金属橡胶减振器冲击试验时,能够很好地描述减振器在受到冲击载荷后的加速度响应特征,其结果误差见表2。冲击加速度响应到达峰值的时刻,数值模拟的计算值滞后试验值;加速度响应峰值的试验值大于数值模拟的计算值。冲击高度由150 mm增加到250 mm的过程中,由于冲击高度的增加导致Sprng-Dampr165单元变形量增加,准静态试验得到的刚度与实际刚度之间误差增大,致使数值模拟计算误差增大。
2.3.2 相对密度对冲击性能的影响
考虑金属橡胶减振器的影响因素时,其相对密度是不可忽略的。金属橡胶的非线性刚度和阻尼取决于其相对密度的变化,其固有频率取决于刚度。对相对密度为0.20、0.25和0.30的金属橡胶减振器进行数值模拟,对其施加如图15所示的半正弦激励信号。
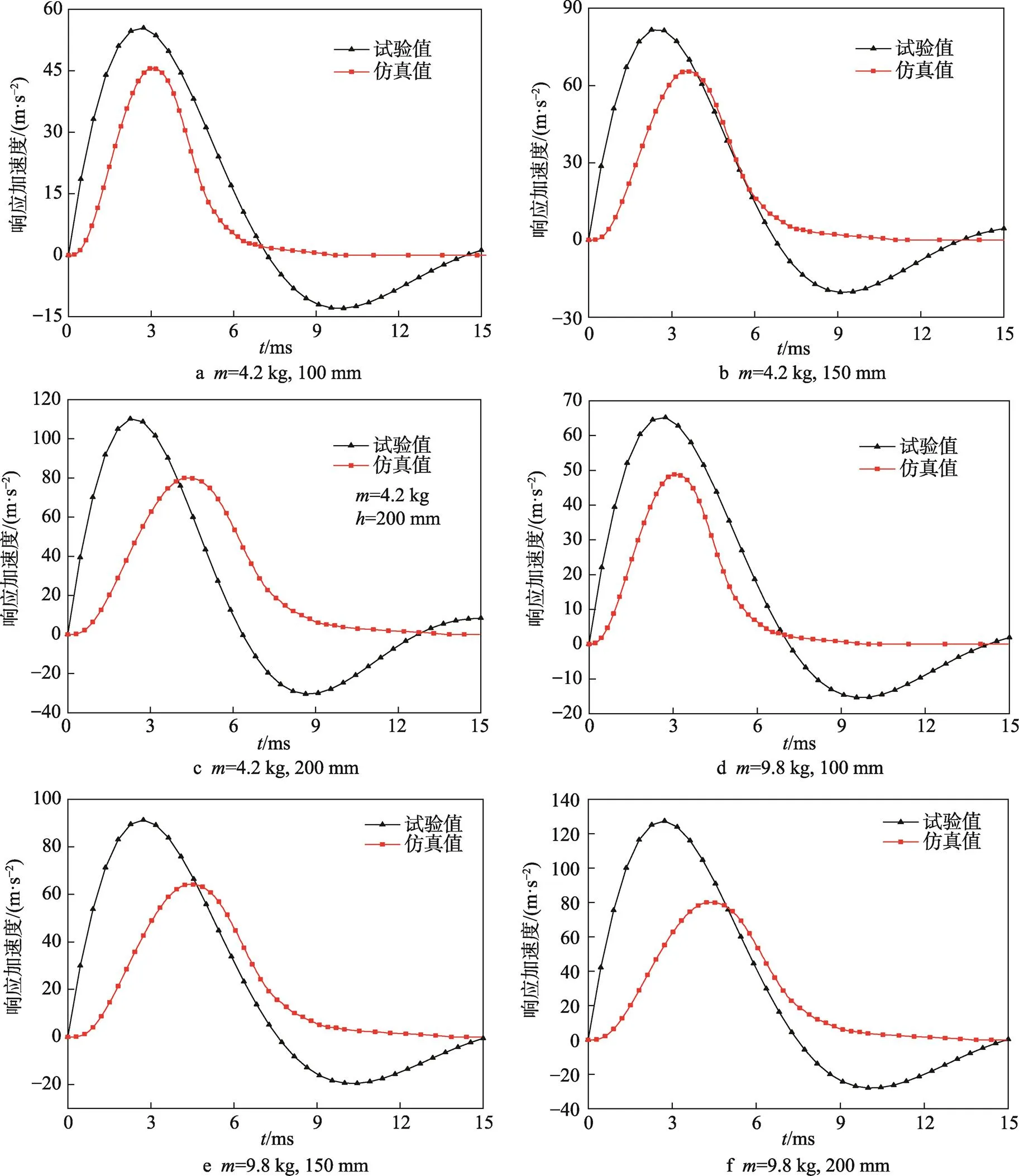
图14 试验结果和数值模拟计算结果对比
表2 冲击试验结果和数值模拟结果对比

Tab.2 Comparison between shock test results and numerical simulation results
由图15可知,响应加速度曲线的峰值明显低于激励加速度曲线的峰值,其到达峰值的时刻晚于激励加速度的峰值时刻。由表3可以看出,金属橡胶的相对密度在0.20~0.30区间增加时,响应加速度峰值由29.0472上升到31.7765,到达峰值时间由1.543 ms下降到1.441 ms,冲击隔离系数由0.5928上升到0.6485。这表明,随着相对密度增加,金属橡胶的抗冲击性能变差。这是因为相对密度的增加,内部金属丝之间接触对增多,摩擦力增大,导致金属橡胶的刚度增大,导致其抗冲击性能变差。
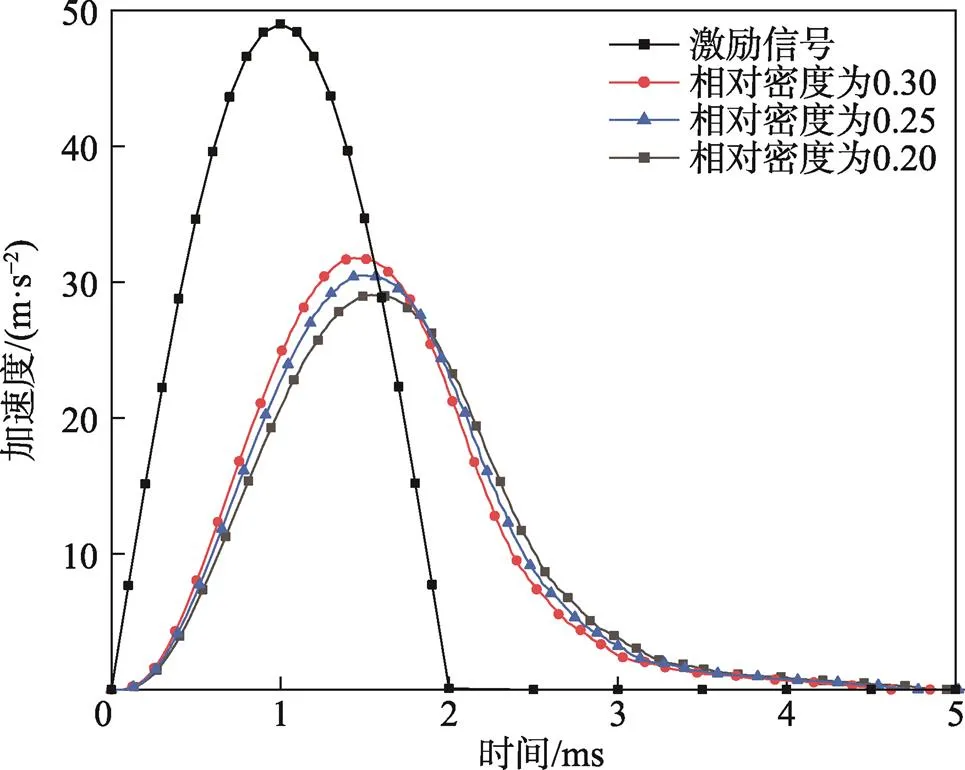
图15 不同相对密度减振器的响应加速度曲线
表3 不同相对密度减振器的冲击隔离系数
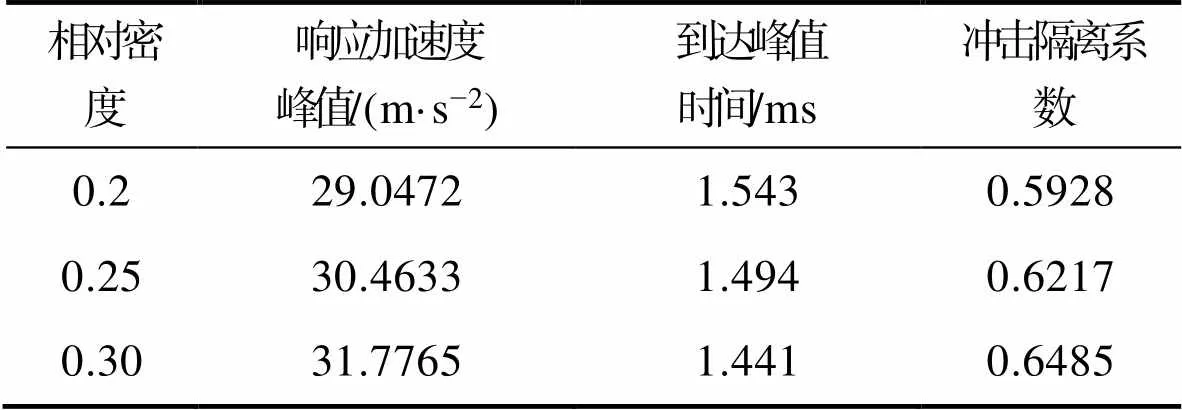
Tab.3 Shock isolation coefficient of dampers with different relative densities
2.3.3 激励峰值对冲击性能的影响
随着脉冲信号激励峰值的增加,减振器失效的可能性也会增加。研究不同峰值作用下的冲击性能将为减振器的设计提供一定的理论依据,因此,对相对密度相同的金属橡胶减振器进行数值模拟,对其施加半正弦激励信号,其脉冲宽度为2 ms,激励峰值为2~10;各激励峰值减振器的响应加速度曲线,见图16。
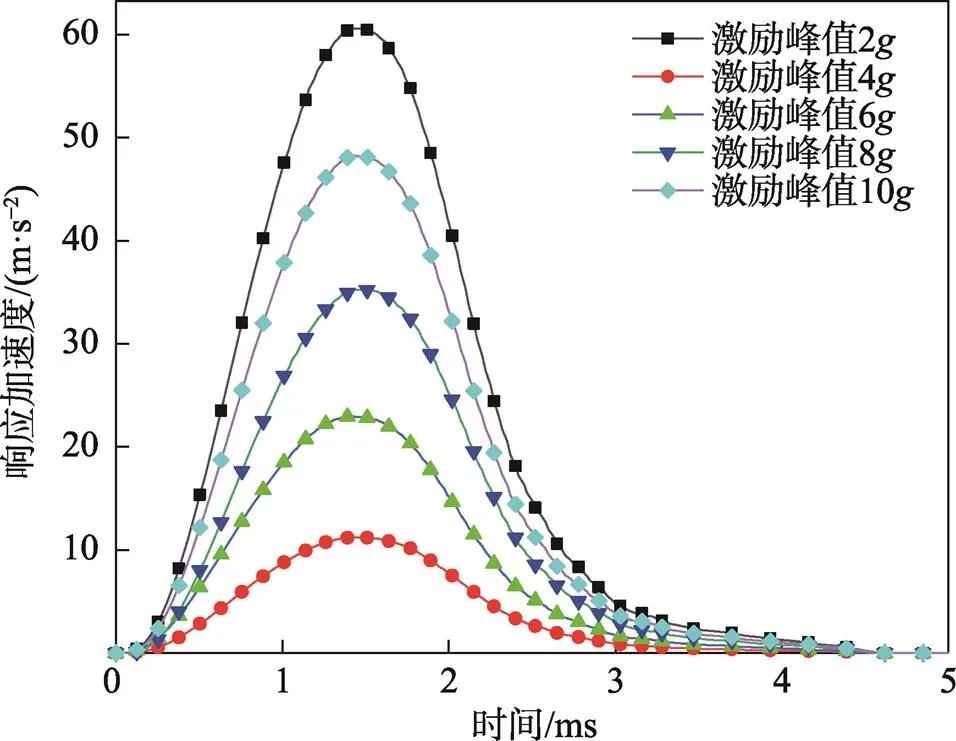
图16 不同激励峰值的响应加速度曲线
由表4可以看出,激励加速度峰值在2~10区间增加时,到达峰值时间由1.466 ms下降到1.454 ms,冲击隔离系数由0.5727上升到0.6186。这表明,随着激励加速度峰值的增加,其抗冲击性能随激励峰值的增大而变差。这是由于激励峰值的增加,金属橡胶减振器的振动峰值增加,导致金属橡胶的刚度增大,减振缓冲效果减弱,从而其抗冲击性能变差。
表4 不同加载幅值的减振器抗冲击特性评价参数
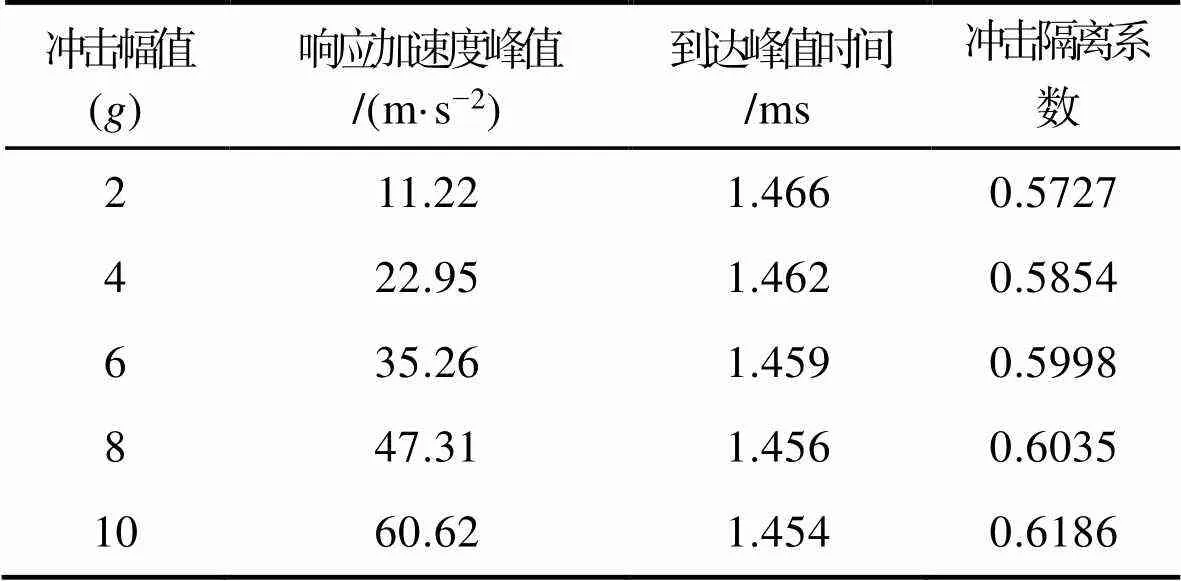
Tab.4 Response acceleration curves of dampers with different loading amplitudes
3 结语
所提出的仿真方法在较小的冲击载荷下,可以较好地模拟金属橡胶减振器的抗冲击特性。随着冲击载荷的激励峰值增加,仿真结果误差增大,误差最大不超过39%。随着相对密度和激励峰值的增加,金属橡胶减振器的抗冲击性能变差,到达峰值的时间减小,冲击隔离系数增加。
[1] 白鸿柏, 詹智强, 任志英. 金属橡胶声学性能研究进展与展望[J]. 振动与冲击, 2020, 39(23): 242-254.
BAI Hong-bai, ZHAN Zhi-qiang, REN Zhi-ying. Progress and Prospect of Acoustic Properties of Metal Rubber[J]. Journal of Vibration and Shock, 2020, 39(23): 242-254.
[2] 李玉龙, 何忠波, 白鸿柏, 等. 金属橡胶的研究及应用进展[J]. 兵器材料科学与工程, 2011, 34(1): 103-108.
LI Yu-long, HE Zhong-bo, BAI Hong-bai, et al. Advances in Research and Application of Metal Rubber[J]. Ordnance Material Science and Engineering, 2011, 34(1): 103-108.
[3] XUE Xin, YANG Pei, SHAO Yi-chuan, et al. Manufacture Technology and Anisotropic Behaviour of Elastic-Porous Metal Rubber[J]. lnternational Journal of Lightweight Materials and Manufacture, 2020, 3(2): 88-99.
[4] REN Zhi-ying, CHEN Qi-sheng, BAI Hong-bai, et al. Study on Damping Energy Dissipation Characteristics of Cylindrical Metal Rubber in Nonforming Direction[J]. Advances in Materials Science and Engineering, 2018(11): 1-10.
[5] 侯军伟, 原霞, 杨伟, 等. 简支梁金属橡胶本构模型[J]. 机械科学与技术, 2021(8): 1299-1304.
HOU Jun-wei, YUAN Xia, YANG Wei, et al. Constitutive Model for Simply Supported Beams of Metal Rubber[J]. Mechanical Science and Technology for Aerospace Engineering, 2021(8): 1299-1304.
[6] 邵晓宙, 樊文欣, 王亚飞, 等. 金属橡胶Mooney-Rivlin修正模型试验[J]. 包装工程, 2021, 42(9): 135-140.
SHAO Xiao-zhou, FAN Wen-xin, WANG Ya-fei, et al. Experimental Investigation on Mooney-Rivlin Modified Model of Metal Rubber[J]. Packaging Engineering, 2021, 42(9): 135-140.
[7] 夏宇宏, 姜洪源, 魏浩东, 等. 金属橡胶隔振器抗冲击性能研究[J]. 振动与冲击, 2009, 28(1): 72-75.
XIA Yu-hong, JIANG Hong-yuan, WEI Hao-dong, et al. Shock Protection Characteristics of Metal Rubber Isolators[J]. Journal of Vibration and Shock, 2009, 28(1): 72-75.
[8] 闫辉, 姜洪源, 刘文剑, 等. 金属橡胶隔振器随机振动加速度响应分析[J]. 物理学报, 2010, 59(6): 4065-4070.
YAN Hui, JIANG Hong-yuan, LIU Wen-jian, et al. Analysis of Acceleration Response of Metal Rubber Isolator under Random Vibration[J]. Acta Physica Sinica, 2010, 59(6): 4065-4070.
[9] 卢成壮, 李静媛, 周邦阳, 等. 金属橡胶的刚度特性和阻尼试验研究[J]. 振动与冲击, 2017, 36(8): 203-208.
LU Cheng-zhuang, LI Jing-yuan, ZHOU Bang-yang, et al. An Experimental Study on Stiffness Characteristics and Damping of Metal Rubber[J]. Journal of Vibration and Shock, 2017, 36(8): 203-208.
[10] 朱彬, 马艳红, 张大义, 等. 金属橡胶迟滞特性本构模型研究[J]. 物理学报, 2012, 61(7): 474-481.
ZHU Bin, MA Yan-hong, ZHANG Da-yi, et al. A Constitutive Model of Metal Rubber Based on Hysteresis Property[J]. Acta Physica Sinica, 2012, 61(7): 474-481.
[11] 朱彬, 马艳红, 洪杰. 金属橡胶刚度阻尼模型理论分析[J]. 北京航空航天大学学报, 2011, 37(10): 1298-1302.
ZHU Bin, MA Yan-hong, HONG Jie. Theoretical Analysis on Stiffness and Damping Characteristics of Metal Rubber[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(10): 1298-1302.
[12] MA Yan-hong, ZHANG Qi-cheng, ZHANG Da-yi, et al. The Mechanics of Shape Memory Alloy Metal Rubber[J]. Acta Materialia, 2015, 96: 89-100.
[13] YANG Pei, BAI Hong-bai, XUE Xin, et al. Vibration Reliability Characterization and Damping Capability of Annular Periodic Metal Rubber in the Non-Molding Direction[J]. Mechanical Systems & Signal Processing, 2019(132): 622-639.
[14] 唱忠良, 刘松, 邹广平, 等. 金属丝网橡胶减振器冲击响应有限元仿真研究[J]. 哈尔滨工程大学学报, 2018, 39(9): 1505-1510.
CHANG Zhong-liang, LIU Song, ZOU Guang-ping, et al. Finite Element Simulation on Shock Response of Metal-Net Rubber Damper[J]. Journal of Harbin Engineering University, 2018, 39(9): 1505-1510.
[15] 刘泽. 金属丝网橡胶减振器振动及抗冲击力学性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2016: 71-84.
LIU Ze. Vibration and Shock Resistance Mechanics Performance of Metal-Net Rubber Damper[D]. Harbin: Harbin Engineering University, 2016: 71-84.
Finite Element Simulation of Shock Resistance of Metal Rubber Damper
BAO Ji-xuan, YUAN Xia, XUE Shuang-qiao, XU Shao-nan, MA Yi-lin, WANG Zhao-hui
(School of Mechanical Engineering, North University of China, Taiyuan 030051, China)
The work aims to propose a numerical simulation method of metal rubber for engineering calculation, so as to provide a theoretical basis for preparing metal rubber materials with good damping properties. A finite element model of metal rubber damper was established, and the metal rubber material was defined by Sprng-Dampr165 element. Through numerical simulation, the effect of different load masses on the shock resistance was calculated, and the feasibility was analyzed comparatively. According to the finite element results, the maximum error of response acceleration peak was 27.72% when the load mass was 4.2 kg. When the load mass was 9.8 kg, the maximum error was 38.15%, and the test results had the same trend as the finite element results, which verified the feasibility. When the impact load is small, the proposed numerical simulation method has a good performance in simulating the shock resistance of metal rubber damper.
metal rubber; nonlinear stiffness; shock resistance; spring damping element
TB485.1;U260.34+2
A
1001-3563(2022)05-0136-07
10.19554/j.cnki.1001-3563.2022.05.019
2021-06-09
山西省重点研发计划国际科技合作项目(201903D421035)
鲍继轩(1995—),男,中北大学硕士生,主攻振动与噪声控制。
原霞(1976—),女,博士,中北大学副教授,主要研究方向为振动与噪声控制、滑动轴承。
