复合场问题中的两个拓展运动模型剖析

■山东省齐河县第一中学 冯宗国

复合场问题中的螺旋线运动模型与摆线运动模型在近几年的高考试题中均有所考查,下面通过模型的讲解、典型例题的剖析、同类型试题的训练等三个环节对螺旋线运动、摆线运动这两个复合场中带电粒子的运动模型进行系统梳理,以期对同学们的复习备考有所帮助。

一、螺旋线运动模型

1.模型讲解。

情景1:如图1所示,带正电粒子的初速度大小为v0,方向与匀强磁场方向间的夹角为θ。

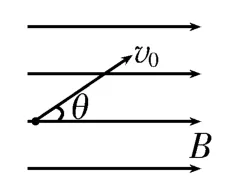
图1

分析:以磁场的方向为x轴正方向建立如图2所示的三维直角坐标系,可以将初速度v0分解为vx=v0cosθ,vy=v0sinθ。粒子因有分速度vy而受到yOz平面内的洛伦兹力,在x轴方向上不受力。粒子在x轴方向上以速度vx做匀速直线运动,在yOz平面内以速度vy做匀速圆周运动,这两个分运动是相互垂直的,其合运动的轨迹类似于弹簧(如图3所示),这种运动称为等距螺旋线运动。

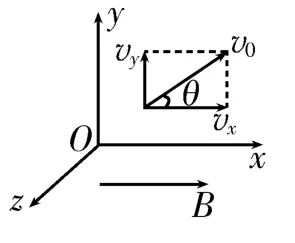
图2

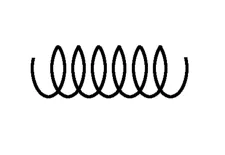
图3

拓展1:如图4所示,在上述模型中加入与匀强磁场同向的匀强电场,则粒子在x轴方向上不受洛伦兹力,只受静电力。粒子在x轴方向上做初速度为vx,加速度为的匀加速直线运动;在yOz平面内仍做匀速圆周运动。其合运动的轨迹为不等距螺旋线。

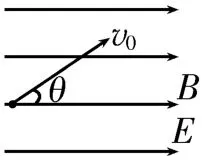
图4

2.典型例题剖析。

例1如图5所示,在三维直角坐标系中,沿z轴正方向有磁感应强度为B的匀强磁场,沿z轴负方向有电场强度为E的匀强电场。在原点O有一质量为m,电荷量为-q的粒子(不计粒子自身重力)以沿x轴正方向,大小为v的初速度发射。试求粒子在时刻的位置坐标。

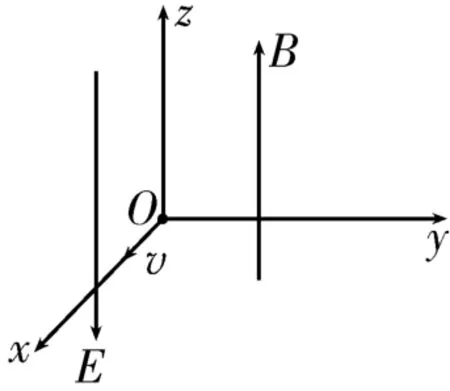
图5

解析:粒子在z轴方向上做初速度为零,加速度为的匀加速直线运动;在xOy平面内做匀速圆周运动。其合运动的轨迹为不等距螺旋线。根据,解得。粒子在xOy平面内做匀速圆周运动,其运动轨迹(俯视图)如图6所示。根据粒子做圆周运动的周期,易知粒子在时间内的运动轨迹所对的圆心角为。根据洛伦兹力提供向心力得qvB=,结合图示得粒子在时刻的位置坐标为。

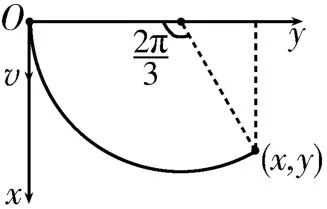
图6

3.训练提升。

练习1:如图7所示,M为竖直放置的金属板,N为记录板,分界面P将M、N两板间的区域分为宽度均为d的Ⅰ、Ⅱ两部分,M、N、P所在平面相互平行,a为M板上的小孔。区域Ⅰ、Ⅱ内分别充满平行于M板水平向里的匀强磁场B和匀强电场E。一质量为m,电荷量为+q的粒子,从a孔以初速度v0进入磁场,过分界面P上的b点(图中未画出)进入电场,最终打到记录板N上。不计粒子自身重力。以初速度v0所在直线为z轴,取向右为正方向,取z轴与记录板N的交点O为坐标原点,以平行于记录板N水平向里为x轴正方向,以竖直向上为y轴正方向,建立三维直角坐标系。求:

图7

(1)b点到z轴的距离L。

(2)粒子打到记录板N上时的x轴坐标。

提示:(1)粒子在区域Ⅰ内做匀速圆周运动,根据洛伦兹力提供向心力得qv0B=,解得。根据几何关系得L=,解得。

(2)设粒子在区域Ⅰ内的运动轨迹所对的圆心角为α,根据几何关系得cosα=。粒子从b点进入区域Ⅱ,在yOz平面内做匀速直线运动,在xOy平面内做匀加速直线运动。在z轴方向上满足vz=;在x轴方向上满足qE=。联立以上各式解得x=。

二、摆线运动模型

1.模型讲解。

情景2:如图8所示,在竖直向下的匀强电场与垂直于纸面向里的匀强磁场的复合场中,带正电的粒子具有水平初速度v0,已知电场强度为E,磁感应强度为B,且。

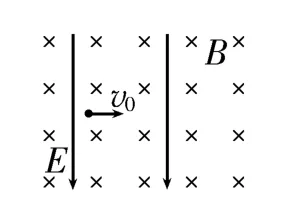
图8

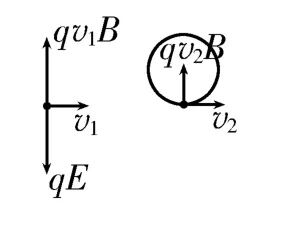
图9

图10

拓展2:若将上述模型中的带电粒子由静止释放,则可将初速度(v0=0)分解为v1=,即粒子一边做匀速直线运动,一边在释放点以下沿逆时针方向做匀速圆周运动。

2.典型例题剖析。

例2如图11所示,在竖直平面内有垂直于该平面(纸面)向里的匀强磁场,磁感应强度为B。竖直平面内的a、b两点在同一水平线上,相距为L。带电荷量q＞0,质量为m,重力不可忽略的粒子P,以初速度v从a点对准b点射出。不计空气阻力,不考虑粒子P与地面接触的可能性,粒子P通过b点。

图11

(1)求L的可能值,以及对应的粒子P从a点运动到b点所经过的时间t。

(2)对满足(1)问要求的L值,粒子P能否从a点由静止释放后也可以通过b点? 若能,求粒子P在运动过程中可以达到的最大速率vmax。

解析:(1)若粒子P做匀速直线运动,则粒子P受力平衡,即qv1B=mg,解得粒子P的速度。当v=v1时,L为任意值,。当v≠v1时,粒子做摆线运动。每经过一个圆周运动的周期,粒子就回到初始高度。粒子P从a点运动到b点所经过的时间)。因为粒子P完成一个完整的圆周运动不会产生位移,所以。

(2)将粒子P从a点由静止释放属于v≠v1的情况,显然它可以通过b点。粒子P在a点以下做圆周运动初始时刻的速度。当粒子P两个分运动的速度同向时,合速度最大,最大速率vmax=v1+。

3.训练提升。

练习2:如图12所示,空间存在一复合场,匀强电场竖直向下,匀强磁场垂直于纸面向里,x轴正方向水平向右。一质量为m,带电荷量为+q的小球以大小不同的初速度从O点沿x轴正方向射出。已知电场强度为E,磁感应强度为B,重力加速度为g。

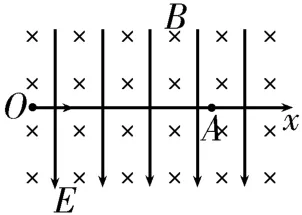
图12

(1)若小球做直线运动到达A点,求初速度的大小v0。

(2)若小球由静止释放,则它会做曲线运动通过A点,求A点的横坐标和小球离开x轴的最大距离。

提示:(1)若小球做直线运动,则小球受力平衡,即qv0B=mg+qE,解得v0=。

(2)将小球由静止释放,小球的曲线运动可视为速度为v0的匀速直线运动和速度为v0的匀速圆周运动的合运动,即摆线运动。根据,解得小球做圆周运动的半径,周期T=。要使小球通过A点,则需满足xA=v0t,t=nT(n=1,2,3,…),解得xA=。根据几何关系可知,小球离开x轴的最大距离d=。

综上所述,螺旋线运动与摆线运动均是匀速圆周运动与直线运动的合运动。不同的是,螺旋线运动的两个分运动是相互垂直的,摆线运动的两个分运动是共面的。当带电粒子的初速度具有沿磁场方向(或反方向)的分量时,可以考虑是不是螺旋线运动。当带电粒子受到的洛伦兹力与静电力(或重力) 不能抵消时,可以考虑是不是摆线运动。分析螺旋线运动和摆线运动这两个运动模型都体现了分解的思想。在处理螺旋线运动时,还采用了降维思想。在处理摆线运动时,引入了速度选择器的速度,还体现了补偿思想。