细长旋成体亚声速超大攻角非定常流动特性研究
2022-03-20王方剑王宏伟李晓辉
王方剑 王宏伟 李晓辉 董 磊 黄 湛 陈 兰
(中国航天空气动力技术研究院,北京 100074)
引言
空空导弹作为现代空战的主要攻击手段,要求比目标飞机更高的机动性和敏捷性.新型空空导弹在面对新一代飞机时必须具备全方位攻击能力,尤其对来自后方目标的威胁,则需要更高转弯率和更大机动包络线的航向反转机动等先进高效机动方法.为了保证高效机动的顺利完成,要求导弹在超大攻角(α=0°~ 180°)范围内具有飞行和机动控制能力[1].以往对超大攻角流动的观测和研究大多集中在α=40°~ 60°范围内,最大角度不超过90°[2-14].在超大攻角条件下,复杂的非定常分离流问题广泛存在,包括非定常涡的产生、脱落、干扰和非定常非对称等气动现象[2-10].因此,提高对细长体复杂非定常气动特性的认识尤为重要.
早在20 世纪50 年代[3],对细长体(锥柱体)分离流动特性的探索就已经开始.在小攻角处,细长体背风侧形成对称的轴向集中涡[4].随着攻角的增大(达到30°左右),流型由对称型转变为非对称型.随着旋涡沿轴向向后发展,旋涡一个接一个离开物面,形成旋涡脱落流动结构,并以一定角度向下游流动.此时如果观察其横截面,会发现形成类卡门涡街的流动形式[5].
在无侧滑来流条件下的侧向力是非对称涡的重要标志[9-10].Lamont 和Hunt[11]的研究表明,在大部分攻角范围内(0°~ 90°),沿旋成体轴向的侧向力呈振荡分布.Dexter[12]发现侧向力强烈依赖于旋成体滚转角.在一个可独立滚转的头尖部上进行的风洞试验表明,滚转角所造成的对侧向力的影响主要头尖部带来.Luo 等[13]在一个椭圆形截面头尖部的旋成体上进行了压力分布测量,结果表明,椭圆形截面头尖部侧向力随滚转角的变化规律比圆形更容易预测,且两种头尖部的最大侧向力基本相同.通过在头尖部附近安装一根可伸缩的钢丝[14]或沙砾[15],可以通过改变头尖部的周向角来有效地控制侧向力的方向.大多数文献采用的试验模型是头部尖锐的旋成体外形,然而头部形状也会对流动产生一定影响.Hsieh 等[16-17]对半球形头部旋成体在攻角从0°~50°的工况下的分离流进行了试验和数值研究.令人惊讶的是,分离流包含了许多复杂的流动结构特征,这是三维流所独有的.结果表明,半球形头部旋成体同时存在两个分离区(头部分离泡和横流分离区).
20 世纪80 年代以前,由于缺乏强大的计算软件和先进的风洞试验方法,学者们关注点主要集中在附着流和稳定分离区上[18].随着技术的发展,一些非定常流动特性被揭示出来.Zeiger 等[19]对细长旋成体的流动特性进行流动显示水洞试验,认为在大攻角时,细长体旋成体上的流动可主要分为3 种流动形态,第1 种流动形态是头尖部附近的产生的较为集中的涡旋,随着流动沿轴向向后发展,流动结构逐渐体现为旋涡脱落流动形态(第2 种流动形态),涡脱落方向与旋成体呈一定角度,当流动发展至接近底部时(横截面位置X/D 从10 到32),脱落的旋涡涡轴与旋成体平行,形成第3 流动形态.管小荣和徐诚[20]、杨云军和周伟江[21]、张赢和刘超峰[22]、刘仙名和符松[23],采用数值模拟方法细致的研究了非对称旋涡的演化与发展,研究表明不同的Re、湍流模型均会对旋涡非对称流动的模拟产生一定影响.Degani 和Zilliac[24]的研究表明,其非定常流动主要包括类卡门涡街的低频流动、剪切层失稳引起的高频流动,以及介于以上两种频率之间的旋涡干扰流动.Ayoub 和Karamcheti[25]同时测量了细长旋成体表面压力和尾流速度波动.结果表明,在头部区域存在一定的旋涡脱落现象.在离旋成体头部不同距离处,涡脱落产生了一个接近10.5 Hz 的频率.
除此之外,马赫数对旋成体分离流动细节也有一定影响,Keneer[26]对旋成体前体在不同马赫数及攻角细长体流动进行研究,在风洞试验纹影照片中可以观察到,第一脱落涡在高亚声速下(Ma=0.6)的轨迹比低速(Ma=0.25)时更接近表面,侧力系数从Ma=0.25 时的1.9 降至Ma=0.6 时的0.8,同时也可以看到,在Ma=0.6 时,攻角55°时后半部分出现不对称,旋涡较为分散,而Ma=0.25 在此攻角下攻角还较为集中,这体现出旋成体高亚音速流动与低速旋涡流动相比,分离流动的旋涡位置、旋涡强度、涡破裂位置、分离位置均有一定的不同.
在传统的复杂分离流动数值模拟工作中,基于雷诺平均Navier-Stokes (RANS)方程的流场预测方法对附着流以及小分离流动有较好的模拟能力,计算成本较低,是工程运用中最广泛的一种方法,但由于RANS 方法平均了小尺度的旋涡脉动,难以精细的模拟较大范围的分离与复杂的旋涡流动.大涡模拟方法(LES)能够较好的模拟大范围分离旋涡流动现象,但对边界层的网格密度有非常高的要求,带来很大的计算成本.所以为了结合RANS 方法与LES方法的优势,Spalart[27]提出了基于S-A 湍流模型的DES 方法,引入特征长度参数,根据特征长度选择不同的流动模拟方法,在近壁面区域,采用RANS 方法,在远离物面的区域,选择LES 方法进行模拟,能够兼顾数值计算精度与效率.深入研究发现,DES 方法会发生模型应力耗散现象(modeled stress depletion,MSD),导致在流动中出现网格诱导分离问题(grid induced separa-tion,GIS).2006 年,Spalart 等[28-37]提出了延迟脱体涡模拟方法(DDES)有效解决MSD与GIS 问题,该方法被广泛应用于圆柱扰流、空腔流动和起落架分离流动能计算研究中.
从细长体大攻角的研究情况来看,之前对细长体大攻角流动研究速域主要集中在低速,并且研究攻角范围主要在α=0°~ 90°之间,本文针对细长旋成体在高速(Ma=0.6)超大攻角下(α=0°~ 180°)存在的旋涡非定常性、旋涡脱落和旋涡非对称等复杂流动现象,采用基于结构网格的DDES 数值方法,开展细长旋成体复杂气动非定常特性研究,为新型机动导弹超大攻角气动设计提供理论支撑.
1 研究方法
本文采用数值模拟与油流显示风洞试验相结合的方法来研究细长体超大攻角流动特性问题.其中数值模拟采用Roe 方法求解Navier-Stokes 方程,细致分析细长体超大攻角在不同攻角下的非定常流动特性及压力脉动特性,油流显示风洞试验用于获得细长体模型表面的流动拓扑,通过对比试验结果与数值结果,验证数值模拟结果的准确性.
1.1 数值方法与算例验证
控制方程为三维可压缩Navier-Stokes 方程,广义坐标表示为

空间离散采用基于MUSCL 方法插值方法的FDS-Roe 格式,黏性项采用二阶中心差分离散,对流和压力项使用3 阶迎风格式.时间推进格式为隐式LUSGS 方法,保证了较高的时间计算精度.非定常计算采用双时间步长方法,同时采用多重网格算法加快子迭代的收敛速度.
在用湍流模型进行流动模拟时,控制方程中应加入雷诺应力相关项.本文采用的湍流模型是基于Menter 的两方程剪切应力输运湍流模型(SST),表达式为

DES 方法的扩展形式是基于SST 湍流模型,其中湍流尺度为

DES 长度尺度dDES表示为

式中,Δ 为当前网格单元与周边单元的最大距离,CDES是SST 湍流模型中附加的经验模型常数,CDES表示为


为了解决MSD 与GIS 问题问题,Spalart[27]提出了延迟函数fd,将SST 湍流模型的湍流能量输运方程的耗散项重新定义为与网格尺度和湍流黏度有关的DES 长度尺度,结合延迟函数fd的长度尺度dDES被重新定义为

因此,dDES不仅与网格尺度有关,而且与湍流黏度有关,可以防止湍流模拟过早地切换到LES 模式.
算例验证采用高雷诺数圆柱扰流算例进行计算,圆柱直径为D=457 mm,圆柱长度为5.66D,圆柱两端采用对称边界条件,其他边界采用自由来流条件.图1 为圆柱扰流计算域,为保证满足自由来流边界条件,在流向计算域为30D,图2 是圆柱横截面网格.计算参数为:Ma=0.25,Re=3 × 106,物理时间步长为Δt=4 × 10-4s,一共计算5000 个物理时间步,计算物理时间为2 s.

图1 圆柱扰流计算域Fig.1 Domain of calculation

图2 圆柱横截面网格Fig.2 Zoomed-in-view of mesh around the cylinder
图3 是圆柱扰流压力分布试验值[38-40]与计算值压力分布对比,其中纵轴是压力系数,横轴是方位角θ,计算值是截取了圆柱中间截面(y=2.83D)的压力分布时均值,通过计算获得的圆柱升力斯特劳哈尔数St=0.32,并将取一个周期内的60 个瞬时值进行平均,得到时均值.图中显示,计算值与试验值吻合较好,说明本文所采用的DDES 方法能够较好的捕捉圆柱尾迹的旋涡结构,见图4.

图3 压力分布试验值[38-40]与计算值压力分布对比Fig.3 Comparisons of pressure coefficients distribution[38-40]

图4 圆柱扰流尾迹流动结构Fig.4 Q-criterion iso-surface of wake
1.2 油流流动显示技术
为了便于油流的光学测量技术的应用,试验选定在中国航天空气动力技术研究院FD-12 风洞常规亚跨声速试验段作为流场显示试验的主要试验环境,该试验段长度为3.8 m,试验段横截面尺寸为1.2 m ×1.2 m,两侧沿来流方向对称布置4 个窗口,内芯顶部也具有光学窗口,是目前能够实现常规攻角机构试验光学条件最好的试验段.由于模型需要安装在常规攻角机构上,攻角调节范围是-15°~ 25°,无法实现连续的大攻角变化,需要通过预置攻角模块来实现不同阶段的攻角调节.
如图5,模型为了实现180°可翻转设计安装,头部和尾部均可与支撑段连接,因此,头部需要设计可拆卸段,适合尾部的支撑连接.

图5 模型的支撑设计Fig.5 Support design of experimental model
由前述风洞试验条件可知,常规试验段和攻角机构的攻角调节范围是-15°~ 25°,流动显示试验模型为了在风洞中实现0°~ 180°的攻角变化,需要对模型的攻角进行预置.在0°~ 30°范围内,预置-15°的攻角,在60°~ 90°范围内,预置-75°的攻角,配合模型头尾更换,可以实现模型0°~ 180°的攻角变化.
传统油流试验,一般在风洞运行结束后,对表面油流图像进行拍摄,获取表面流动结构.在高速、大攻角条件下,较强的流动分离、风洞台阶波干扰、油流自身重力等时刻在影响着表面流动图谱,而暂冲式风洞关车时气流冲击对表面流动影响非常大,风洞运行结束后的表面流动图谱可能与风洞运行时的表面流动图谱纯在明显差别.因此,本试验采用实时化表面油流图像拍摄方法,在风洞运行时,按照下图布局进行拍摄.同时,选取特定工况进行精细化的荧光油膜摩阻测量试验,采用紫外光源的照明系统、混有荧光指示剂的油膜、带有高通滤波片的图像采集系统,针对模型局部区域进行试验拍摄,见图6.

图6 油流流动显示试验测量布局Fig.6 Oil-flow visualization test measurement layout
2 细长旋成体外形及网格
现代高机动导弹除了细长弹身外,还具有鸭舵、尾翼等控制部件,Wang 等[41]的研究结果显示,对于细长导弹大攻角流动,其非定常特性、频率特性主要由细长弹身诱导,弹翼贡献较小,所以为了能够更清晰的研究超大攻角下的流动,本文采用的细长旋成体外形.如图7,弹身直径为60 mm,弹身全长为707.7 mm,弹身头部采用的是尖型头部设计,坐标设置为X 轴向后,Z 轴向上.

图7 细长旋成体外形 (单位:mm)Fig.7 Slender revolutionary body (unit:mm)
计算网格采用结构网格进行求解,如图8,采用O 型网格拓扑,外边界距离的设置以能够满足自由来流条件为判断准则.贴近物面的第一层网格厚度保持Y+~ 1,以确保边界层的准确模拟.为了能够精确的捕捉细长旋成体背风侧的分离涡流动,在模型的法向进行了整体加密,在模型背风侧展向网格进行适当加密,同时当攻角超过90°时,底部超前,这时底部引起的回流区模拟也非常重要,此时会在尾部附近进行加密,总网格量为1500 万.

图8 细长体网格Fig.8 Mesh of slender revolutionary body
由于本文针对大攻角下非定常流动特性问题,其对旋涡尺度的分辨以及旋涡频率特性的捕捉十分重要,所以需要对网格与时间步长无关性进行检查,即确定数值模拟结果不再随网格规模与时间步长大小而变化.因此本文对典型工况(Ma=0.6,α=60°)进行模拟,并选取升力CL与阻力Cd的平均值,以及侧向力的斯特劳哈尔数St 进行分析.首先进行网格无关性验证,采用了3 套计算网格,3 套网格在流向、周向和法向均进行变化,网格量分别为530 万、1500 万和4200 万,图9 展示了3 套网格的物面网格分布.表1 为3 套网格下的升力CL、阻力Cd、侧向力St 计算结果.从表1 我们可以看到,网格规模对CL,Cd与St 均有一定的影响,随着网格量的增加,当网格量达到1500 万时,其计算结果(CL,Cd,St)与网格量4200 万较为接近,证明网格量1500 万对于研究该问题已满足要求.

表1 网格无关性Table 1 Sensitivity of mesh resolution
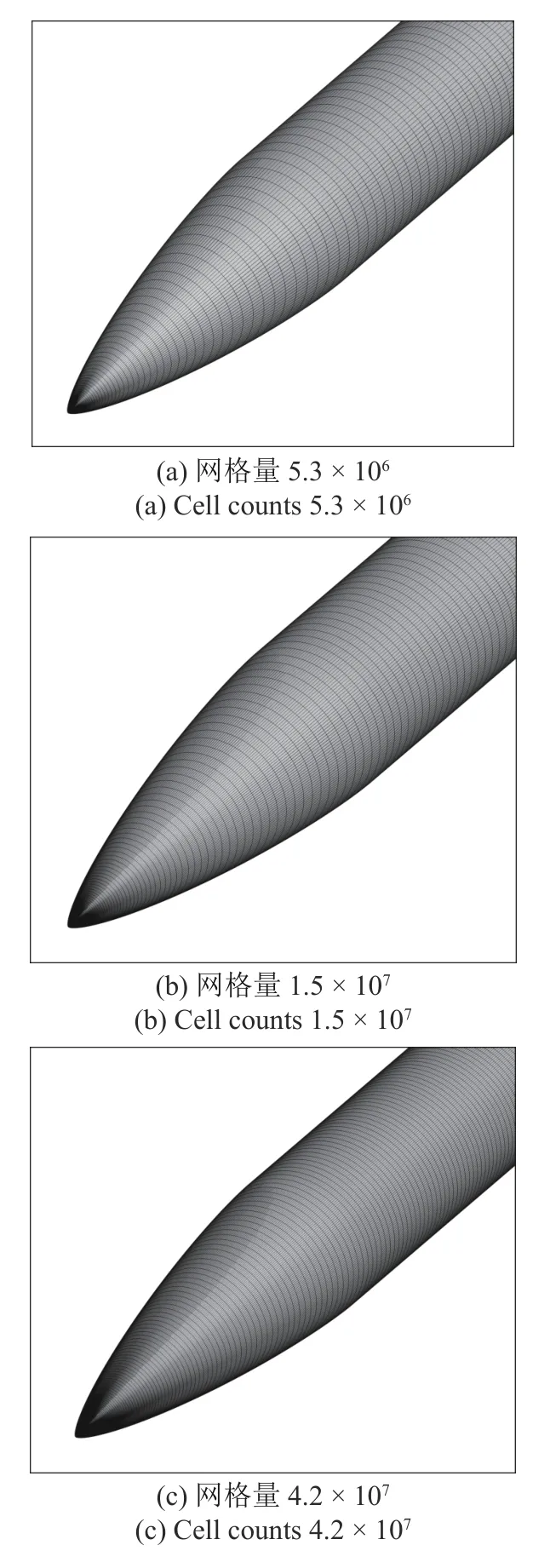
图9 3 套不同规模网格示意Fig.9 Three grids with different cell counts
在时间步长无关性方面,分别采用物理时间步长为dt=1.2 × 10-5s,2.3 × 10-5s,5 × 10-5s 进行计算,网格量为1500 万.表2 为不同时间步长下的计算那结果,从表2 中我们可以看到,时间步长的变化对升力CL、阻力Cd影响不大,但对St 影响相对较大,随着时间步长不断减小,当时间步长达到dt=2.3 × 10-5s 时,CL,Cd与St 基本不随时间步长而变化,证明时间步长dt=2.3 × 10-5s 能够满足研究要求.

表2 时间步长无关性Table 2 Sensitivity of physical time step
3 超大攻角瞬时流动特性
本文采用CFD 数值模拟手段,计算了细长旋成体在攻角α=0°~ 180°下的背风侧流动形态,侧滑角β=0°,雷诺数Re=1.29 × 106m-1,参考长度为直径D=60 mm.由于细长体在大攻角下具有较强的非定常效应,所以这里采用数值模拟得到的瞬时流场与试验进行对比.
图10 为攻角30°,CFD 模拟的表面极限流线分布,以及CFD 与油流试验图像比较,从图中我们可以看到,油流试验与数值模拟得到的主分离线位置较为一致.主分离线在模型头尖部起始并较为靠近背风侧,随着流动沿轴向向后发展,分离线周向位置逐渐向迎风侧移动,当流动发展至弹身圆柱段时,分离线周向位置沿着轴向几乎不变.

图10 CFD 物面流线与油流试验对比(α=30°)Fig.10 Surface streamlines comparisons between CFD and oil-flow test (α=30°)
图11 是攻角30°是旋成体背风侧流动及物面流线,其中背风侧流动通过采用不同截面下的涡量值来体现.从图中可以看到,旋成体背风侧主要呈现出了对称涡的流动形态,旋涡从头部起始,一直沿轴向向后发展至尾部.并且在主旋涡下方靠近物面的位置还存在二次涡流动结构.从物面流线分布也能够看到明显的主分离线以及二次分离线.图12 是X/L=0.1,0.2,0.4,0.6,0.8 截面的压力分布情况,图中显示5 个截面下压力分布均为对称分布形式,体现出旋成体在该攻角的对称旋涡流动结构.

图11 物面流线及空间流动(α=30°)Fig.11 Surface streamlines and flow (α=30°)

图12 各截面压力分布(α=30°)Fig.12 Pressure distribution of cross sections (α=30°)
图13 是CFD 物面流线与油流试验对比图,图中有4 张图,从左至右分别为油流试验拍摄的照片(图13(a)左)、通过试验照片处理出的物面流线图(图13(a)右)、CFD 手段获得物面流线图(图13(b)左)、CFD 获得的横截面流线图(图13(b)右).从图中试验获得的物面流线图(图13(a)左)与CFD 获得的物面流线图(图13(b)左)进行对比发现,存在清晰的主分离线、二次分离线、二次再附线.试验与CFD 获得分离位置与再附位置对比较好.图13(b)也展示了横截面流线,从图中可以看到较为清晰的主分离涡流动结构,同时在物面附近存在较小的二次涡流动结构.

图13 CFD 物面流线与油流试对比(α=60°)Fig.13 Surface streamlines comparisons between CFD and oil-flow test (α=60°)
图14 是攻角在α=60°下的背风侧旋涡流动形态,图中可以看到,在旋成体的前半段(约X/L=0.4 之前),其旋涡流动还较为对称,随着旋涡流动沿轴向向后发展,背风侧旋涡流动逐渐转化为非对称旋涡流动形态.当达到X/L=0.6 截面左右时,旋涡流动变的不再集中,逐渐发展为旋涡脱落的流动形态,此时二次旋涡也变的不再稳定,在物面上也观察不到较为明显的二次分离线.图15 是各截面的压力分布情况,从图中也可以看到,在截面X/L=0.1~ 0.2,其压力分布较为对称.在X/L=0.4 位置,旋涡流动开始出现轻微的非对称形态,随着旋涡向后发展,非对称愈加明显清晰.

图14 物面流线及空间流动(α=60°)Fig.14 Surface streamlines and flow (α=60°)
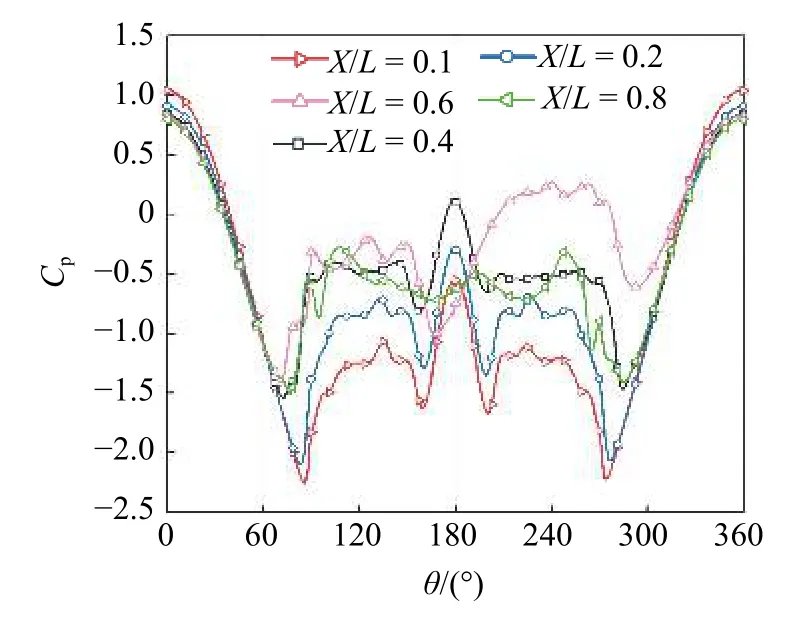
图15 各截面压力分布(α=60°)Fig.15 Pressure distribution of cross sections (α=60°)
图16 是攻角α=90°工况下的流动图像.图中我们可以看到,由于此时旋成体轴线与来流成垂直关系,在背风侧的轴向流动速度很低,所以背风侧无法形成集中涡流动结构,在不同截面下基本都体现出了旋涡脱落的流动现象,并且具有较强的非对称性.从压力分布中(图17)我们也可以看到,由于背风侧旋涡流动主要是涡脱落流动形态,旋涡在物面附近形成的吸力较弱,没有出现吸力峰值.

图16 物面流线及空间流动(α=90°)Fig.16 Surface streamlines and flow (α=90°)

图17 各截面压力分布(α=90°)Fig.17 Pressure distribution of cross sections (α=90°)
图18 是攻角α=120°下油流试验物面流线与CFD 物面流线的对比.从图中可以看到明显的主分离线,CFD 计算结果与油流试验结果吻合很好,没有看到比较明显的二次分离线在模型底部附近均出现了主分离线“弯曲”的现象,这主要是旋成体底部诱导的分离流动的影响.图18 还展示了旋成体在对称面的流动特性,图中我们看到,当来流流过模型的底部时会背风侧产生一个回流区,该回流区在轴向的影响范围约为1.2D.

图18 CFD 物面流线与油流试验对比(α=120°)Fig.18 Surface streamlines comparisons between CFD and oil-flow test (α=120°)
图19 是α=120°攻角下空间流动与物面流线.图中我们可以看到,当自由来流在底部附近产生回流区后,随着流动沿轴向向后发展,背风侧流动逐渐发展非对称旋涡流动,并伴随着一定的旋涡脱落现象.图20 是不同截面下的压力分布情况,可以看到在不同截面下压力分布始终为非对称.

图19 物面流线及空间流动(α=120°)Fig.19 Surface streamlines and flow (α=120°)

图20 各截面压力分布(α=120°)Fig.20 Pressure distribution of cross sections (α=120°)
图21 是攻角150°下试验与数值模拟结果的对比情况.从图中我们可以看到,随着攻角进一步增加,底部分离带来的回流区在模型轴向的影响范围将进一步加大,影响范围约为2.5D.随着流动沿轴向向后发展,模型背风侧逐渐发展为旋涡流动,油流试验中的分离线逐渐清晰起来.图22 是在攻角150°下的空间流动,从图中我们可以看到,旋涡流动在回流区后开始逐渐发展起来,在流动刚流过回流区时,旋涡涡位较低,并且仍然受底部回流区的影响.随着流动继续向后发展,非对称旋涡流动越来越清晰起来,受底部回流区的影响逐渐减弱.

图21 CFD 物面流线与油流试验对比(α=150°)Fig.21 Surface streamlines comparisons between CFD and oil-flow test (α=150°)
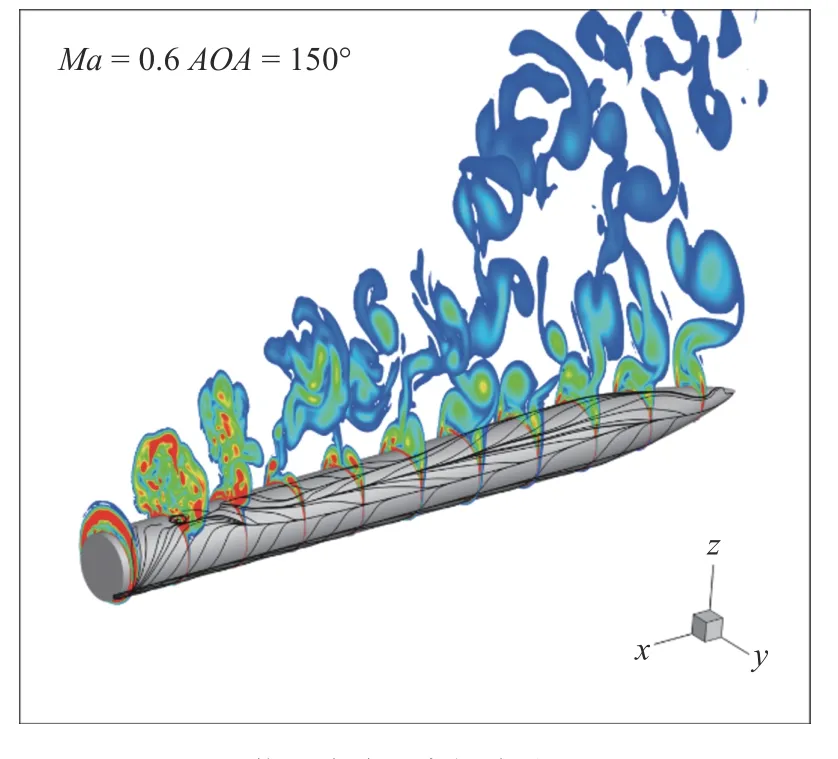
图22 物面流线及空间流动(α=150°)Fig.22 Surface streamlines and flow (α=150°)
图23 是攻角180°工况下物面流线与油流试验的对比情况,图中一共分为上下两张附图,上面附图为CFD 得到物面流线以及对称面的涡量分布图,下面附图为油流试验照片,在此攻角下主要流动特性为底部分离引起的复杂回流流动.从试验以及数值模拟结果我们都可以看到,在底部附近会出现一个十分明显的分离线,并且回流区再附位置主要在距离底部约2.5D 的位置,试验与计算结果对比较好.同时在对称面涡量分布中我们可以看到,来流经过底部时会产生较强的剪切层,随着流动向后发展逐渐失稳,与回流区中的小尺度旋涡流动相互作用,形成较为复杂的具有较强非线性的局部流动.

图23 CFD 物面流线与油流试验对比(α=180°)Fig.23 Surface streamlines comparisons between CFD and oil-flow test (α=180°)
4 超大攻角旋涡流动时序演化
上一节对超大攻角瞬时流动进行分析,但细长体在超大攻角下体现为复杂的非定常流动现象,其背风侧旋涡的强度、位置、涡脱落均会随着时间产生变化,所以本节对超大攻角旋涡流动的时序演化进行分析.本文每个计算物理时间步为Δt=2.3 ×10-5s,共计算2000 个物理时间步,总计算物理时间为0.046 s,以保证足够的时长使得流动进入稳态,并选取后1200 步进行分析.
图24 是攻角α=60°下在X=350 mm 截面背风侧涡量图随时间的变化.从图中我们可以看到,在该截面下背风侧,呈现出了两个集中涡以及两个二次涡,集中涡的涡量和涡位随着时间增加较小,呈现出轻微的非对称流动形态.随着流动沿着轴向向后发展,当流动发展至X=550 mm 截面,如图25,集中涡体现出明显的非对称流动特性,同时随着时间的变化,体现出旋涡脱落特性,产生类卡门涡街式的旋涡交替脱落现象.

图24 截面涡量随时间变化(α=60°,X=350 mm)Fig.24 Vortice of cross section (α=60°,X=350 mm)

图25 截面涡量随时间变化(α=60°,X=550 mm)Fig.25 Vortice of cross section (α=60°,X=350 mm)
图26 是攻角α=90°下在X=350 mm 截面下的涡量图随时间变化.从图中我们可以看到,此时弹身垂直于来流,来流流过弹身后会产生较长的剪切层,随着剪切层逐渐发展,慢慢卷起旋涡,旋涡强度相对较弱,并且旋涡距离物面较远,旋涡对物面的诱导能力较低,没有发现明显的二次涡结构.弹身两侧剪切层诱导的旋涡呈现较为明显的非对称性,并且随着时间增加,旋涡逐渐脱离剪切层向后脱落,左右旋涡的涡脱落现象交替进行.

图26 截面涡量随时间变化(α=90°,X=350 mm)Fig.26 Vortice of cross section (α=90°,X=350 mm)
图27 是攻角α=120°下的X=350 mm 截面涡量图.从图中我们可以看到,此时旋涡距离物面较近,出现了明显的非对称旋涡流动结构,同时在物面附近会诱导出较小尺度的二次涡结构,随着时间发展,左右旋涡的涡位会出现切换现象,涡位较高的旋涡逐渐脱落并飘向尾迹区.图28 是Y=0 mm 的涡量分布图,图中可以看到,在底部附近的回流区存在较多的小尺度旋涡结构,随着时间增加,距离物面较近小尺度涡在物面附近形成回流区,距离物面较远的小尺度涡慢慢脱落飘向尾迹区.弹身(圆柱等直段)附近也存在较强的涡量分布,这是圆柱段集中涡涡量在Y=0 mm 平面的投影,反应出了超大攻角下旋涡具有复杂的三维效应.

图27 截面涡量随时间变化(α=120°,X=350 mm)Fig.27 Vortice of cross section (α=120°,X=350 mm)

图28 截面涡量随时间变化(α=120°,Y=0 mm)Fig.28 Vortice of cross section (α=120°,Y=0 mm)
图29 是攻角α=150°下的X=350 mm 截面涡量图.图中我们可以看到,旋成体背风侧产生了两个集中涡,涡位较低,随着时间增加,旋成体背风侧的涡位出现左右切换的现象,并且随着时间的增加逐渐脱体向下游运动.图30 是Y=0 mm 截面涡量图,来流流过底部后会出现较为明显的剪切层,剪切层逐渐向后发展逐渐失稳变成小尺度涡飘向下游,同时在底部回流区内依然为很多小尺度旋涡流动.

图29 截面涡量随时间变化(α=150°,X=350 mm)Fig.29 Vortice of cross section (α=150°,X=350 mm)

图30 截面涡量随时间变化(α=150°,Y=0 mm)Fig.30 Vortice of cross section (α=150°,Y=0 mm)
图31 是攻角α=180°时在Y=0 mm 截面的涡量分布图,从图中我们可以看到,来流会在底部处拖出明显的剪切层,剪切层逐渐向后发展逐渐失稳,一部分涡量会变成小尺度旋涡向下游发展,另一部分会再附至物面,在头部形成一个回流区,回流区内的小尺度旋涡相互干扰作用,形成复杂的非定常回流流动结构.

图31 截面涡量随时间变化(α=180°,Y=0 mm)Fig.31 Vortice of cross section (α=180°,Y=0 mm)
5 超大攻角物面压力脉动特性
为了更好的对细长体超大攻角下非定常流动频率特性进行分析,如图32 所示,取两个主要截面,一个是X=350 mm 截面,位于模型中间位置,能够较好的描述背风侧由圆柱引起的旋涡流动;另一个是X=550 mm 截面,能够较好的描述模型底部附近流动.在这两个平面内,分别取了一个检测点(m1 点和m2 点),通过提取检测点的压力脉动,可以更深入的分析非定常流动的频域特性.

图32 监测点及截面位置示意图Fig.32 Location of monitored point and cross section
图33 是攻角α=60°下监测点m2 的压力脉动,在此截面流动已经体现出了明显的非定常特性,从测压点的压力脉动就可以看出来,通过对m2 点压力脉动进行频谱分析,发现压力脉动具有主频,主频为f=543 Hz.

图33 监测点压力脉动(α=60°,X=550 mm)Fig.33 Fluctuating pressure of monitored point (α=60°,X=550 mm)
图34 是两个监测点(m1 点和m2 点)的压力系数脉动数据.从图中可以看到,压力脉动较为明显,体现出了明显的非定常性,通过压力脉动进行频谱分析,发现在攻角α=90°下没有发现明显的主频现象,这主要是由于该攻角下,旋涡距离物面较远,对物面诱导能力较弱的原因.
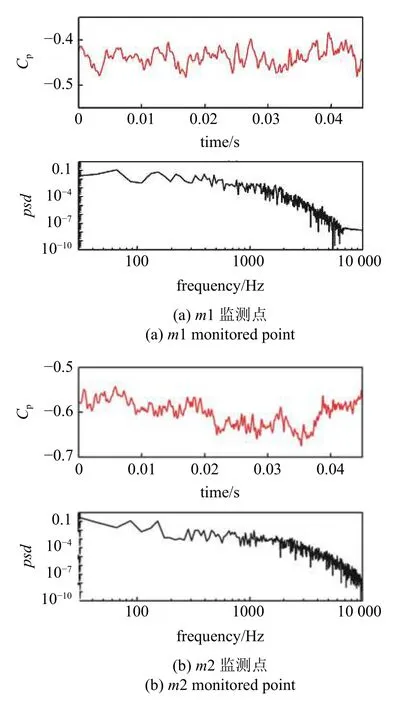
图34 监测点压力脉动(α=90°)Fig.34 Fluctuating pressure of monitored point (α=90°)
图35 展示了监测点m1 和m2 的压力脉动情况,m1 点的压力脉动体现出了圆柱段旋涡的切换情况,从频谱分析中可以看到,该点的压力脉动有一定的主频,主频为f=717 Hz 左右,但是该主频并没有特别集中,这里面也体现出了圆柱段的旋涡结构不仅仅存在较大尺度的集中涡结构,同时也存在较小尺度的旋涡,小尺度涡与大尺度涡相互干扰影响,造成一定程度上的频率分散.m2 点体现出了底部分离回流区的压力脉动特性(如图35(b)),可以看到在m2 点在较低频率(1000 Hz 以内)没有发现主频,但是在高频段出现了较为明显的主频,主频为5391 Hz左右,这主要是在该截面的压力脉动主要由底部分离回流区中的小尺度旋涡带来,小尺度旋涡频率较高,对应压力脉动频率也较高.

图35 监测点压力脉动(α=120°)Fig.35 Fluctuating pressure of monitored point (α=120°)
图36 为α=150°监测点m1 和m2 的压力脉动情况,图中可以看到,集中涡所产生的脉动存在主频,主频为543 Hz 左右.从监测点m2 的频谱分析来看,类似α=120°所发现的高频脉动,在α=150°下的高频脉动为5086 Hz 左右,但是此压力脉动能量较低.

图36 监测点压力脉动(α=150°)Fig.36 Fluctuating pressure of monitored point (α=150°)
图37 是攻角α=180°下m2 点压力脉动,用于监测底部回流区的压力脉动情况.从图中可以看到,底部回流区引起了较高频的压力脉动,脉动频率为f=5173 Hz.

图37 监测点压力脉动(α=180°)Fig.37 Fluctuating pressure of monitored point (α=180°)
从以上分析可以看到,不同攻角下,超大攻角非定常流动体现出了不同的物面压力脉动特性,主要有两类主频,一类为圆柱段非对称旋涡诱导的较低频率,另一类为攻角超过90°时,底部分离流动诱导的较高的频率.本文将特征频率进行无量纲化,提取出脉动主频的斯特劳哈尔数St

式中f 为流动频率,D 为直径,V 为特征速度.对于非对称旋涡诱导的频率,类比圆柱扰流流动,特征速度取横截面流动速度V=V∞sinα,对于底部分离流动诱导的流动频率,特征速度取V=V∞.图38 是不同攻角下的流动St,图中我们可以看到,由非对称涡引起的物面压力脉动主要集中在攻角60°~ 150°,其中流动主频St 范围为St=0.19~ 0.33,而由底部分离诱导的非定常流动在120°~ 180°都有主频,其脉动频率较高,无量纲主频范围为St=1.55~ 1.64.
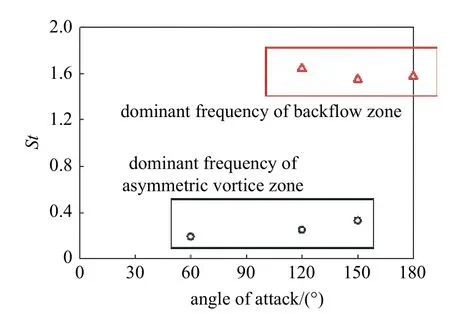
图38 不同攻角下的非定常流动频率St 数Fig.38 St of unsteady flow versus angle of attack
6 结论
本文结合数值模拟DDES 方法与油流显示试验方法,研究了细长旋成体在Ma=0.6 时超大攻角范围内(α=0°~ 180°)的流动特性,得到以下结论.
(1)数值模拟与油流显示试验获得的物面流线吻合较好,在攻角范围α=30°~ 60°和α=150°背风侧旋涡较为集中并且离物面较近时,均能捕捉到明显的分离线、再附线等物面流动拓扑形式,在攻角范围α=90°~ 120°,背风侧旋涡距离物面较远,物面流动拓扑以一次分离线为主,当攻角α=180°时,物面的分离线与再附线主要由底部分离回流区产生.
(2)在攻角范围α=0°~ 90°,细长体背风侧流动特性主要体现为由圆柱段产生的分离涡流动结构,当攻角α=30°时,分离涡位对称集中涡,攻角至α=60°时,细长体头部附近依然为对称涡,在尾部附近非定常非对称涡结构,攻角至90°时,细长体背风侧均为非对称旋涡结构,并伴有多尺度旋涡干扰、涡脱落等现象.
(3)攻角α=120°~ 150°范围内,细长体底部朝前,底部产生较为明显的回流区,回流区内存在较多小尺度旋涡相互作用干扰,随着流动逐渐沿轴向向后发展,流动逐渐发展为非对称涡流动.当攻角达到α=180°时,来流经过底部时会产生较强的剪切层,随着流动向后发展逐渐失稳,与回流区中的小尺度旋涡流动相互作用.
(4)由非对称涡引起的物面压力脉动主要集中在攻角60°~ 150°,其中流动主频St 范围为St=0.19~0.33,而由底部分离诱导的非定常流动在120°~180°都有主频,其脉动频率较高,无量纲主频范围为St=1.55~ 1.64.
本文此次研究旨在对超大攻角下细长体的流动特性有个较为清晰的认识,下一步将对非定常气动特性对机动飞行的影响及其控制策略做进一步研究.
