TSTO 马赫7 安全级间分离问题的数值研究1)

王 粤 汪运鹏, 薛晓鹏 姜宗林

* (中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

** (中南大学航空航天学院,长沙 410083)

引言

在超声速/高超声速条件下,发生在双体构型飞行器中的激波/激波与激波/边界层干扰一般会导致飞行器面临严重的气动力/热问题[1-3],直接影响飞行任务的成败.双体构型飞行器已广泛应用于航空航天任务中,比如导弹的机身与舵翼[1]、运载火箭的逃逸塔与末级[4]、火星探测器着陆舱与降落伞[5]以及两级入轨空天飞行器(two stage to orbit,TSTO)[6]等.TSTO 以低成本、高效率以及可靠性成为现在除运载火箭之外的可重复使用航班化航天运输系统的现实选择,受到了广泛的研究[7-10].TSTO 一般由火箭动力的轨道级和吸气式冲压组合动力的助推级组成[11-12].根据当前的TSTO 的动力匹配,TSTO 一般在高超声速条件下级间分离,会在两级之间产生强烈的激波/激波与激波/边界层干扰,在飞行器表面产生强烈的非定常气动载荷,直接影响两级能否安全分离[13].由于两级之间复杂的气动干扰使得级间分离成为TSTO 的隐形难题,所以充分理解两级间的复杂气动干扰及其流动机理对合理避免两级发生碰撞风险具有重要意义.

TSTO 级间分离中的复杂气动干扰与以下因素相关,比如级间分离来流马赫数(Ma)、雷诺数(Re)以及攻角(α)、两级飞行器机身相对间距及夹角(β)、TSTO 飞行器构型以及两级的相对动态运动等[14-15].这些因素对TSTO 级间分离的影响从20 世纪五六十年代就已经开展了静态和动态研究.对于TSTO级间分离静态研究,Moelyadi 等[16]通过无黏数值模拟研究了不同来流Ma 以及相对位置下TSTO级间分离流动,发现两级之间的强气动干扰是由入射激波、反射激波以及膨胀波相互作用的结果.Kitamura 等[17-18]以及Ozawa 等[19-22]研究了Ma=8.1情况下圆柱球头-三角翼的TSTO 飞行器构型在不同间距下的流动,发现在一定间距条件下,两级之间的流动存在一定的不稳定性,并分析了这种流动不稳定性与IV 型激波干扰的关系,解释了激波干扰导致壁面产生高压、高热流的物理机制.Bordelon等[23]通过风洞试验研究了来流Ma=2.74～ 4.96 下的TSTO 级间分离流动,证明了两级飞行器的气动力主要是受强激波干扰的影响,而且在分离过程中的某些位置,飞行器是静不稳定的.Jia 等[24]对不同轨道级的头部构型下的两级之间气动干扰进行了数值研究,分析了两级表面的压力、热流分布,揭示了两级间不同轨道级头部构型下的流场特性及机制,发现弯锥头部模型可以最大减少轨道级头部压力及热流峰值.

虽然静态的数值模拟或者试验研究在TSTO 级间分离问题上得到了一些有益结果和讨论,但是两级飞行器的相对动态运动引起的流动非定常效应却无法在静态研究中得到体现,所以关于TSTO 级间分离的动态研究极其重要.Brenner[25]通过重叠动网格技术对TSTO 级间分离进行了动态无黏数值模拟,给出了分离过程中的瞬态气动干扰.Cvrlje[14]研究了Ma=6.8 来流下TSTO 级间分离的非定常流动,并且分析了在一定间距下轨道级以给定频率进行俯仰振荡的气动特性,发现在级间分离过程中流动不稳定性对纵向运动稳定性的影响不可忽略.Moelyadi等[26]将轨道级的攻角以及与助推级相对的分离距离以给定的余弦函数变化来控制轨道级的运动,通过动网格技术对TSTO 级间分离过程进行无黏数值模拟,结果表明在分离初始阶段轨道级的气动力/矩发生强烈变化时的非定常动态效应必须小心考虑.Liu 等[6]对TSTO 在Ma=3～ 6 下的级间分离用重叠动网格技术进行了数值模拟,结果发现两级飞行器只有在来流攻角α=-2°条件下可以安全分离.此外,对于其他双体构型飞行器的分离运动,Wang等[4,27-28]研究了Ma=3 情况下3 种外形的火箭逃逸塔分离系统的气动干扰流场,分析了分离距离对流场的影响,发现在逃逸塔与火箭的分离过程中流场的非定常振荡对其安全分离是一个隐含风险.

总的来说,在影响TSTO 级间分离的众多因素中,两级飞行器之间的相对位置及相对运动对TSTO的安全级间分离来说是至关重要的,相对位置决定了两级间的复杂气动干扰类型,而相对运动在两级气动干扰流场引入了非定常效应.大多数关于级间分离的动态研究基本是通过指定分离路径、分离速度、或者运动方式来给定TSTO 的级间分离运动,而关于TSTO 自由的气动分离以及相应非定常复杂流动研究则报道较少.TSTO 飞行器在级间分离过程中为了使两级尽快分开一定距离,可能需要轨道级释放前对其进行机械抬升(抬升角即两级机身夹角(β)),不同抬升角度情况下两级之间的气动干扰会对两级的相对分离轨迹产生重要影响,决定了TSTO 能否安全分离.为了深入理解轨道级机械抬升释放前以及级间分离过程中的两级间流动物理机制,本文使用重叠网格方法,对Ma=7 层流条件下轨道级不同抬升角度(β)下的两级入轨飞行器级间分离流场进行了三维的静态和动态数值研究,对轨道级机械抬升过程的静态和动态干扰流动结果进行了对比,结合TSTO 级间分离前和级间分离过程中的波系结构以及三维分离的拓扑结构分析了级间分离中这种复杂气动干扰流动机制对两级飞行器的影响特性.

1 计算模型与数值方法

1.1 TSTO 模型

本文计算所用的TSTO 模型包括两个楔形分别作为轨道级和助推级,其中省略了两级之间的连接分离系统,几何信息如图1 所示,其中两级模型的对称面与O-XY 平面重合,坐标系原点定义为助推级前缘中点,坐标轴方向如图1 所示.轨道级下壁面与助推级上壁面形成的夹角为轨道级抬升角β.该TSTO构型是参考德国Sanger[29]TSTO 构型进行简化缩比得到的,并且假设两级间的无量纲初始间距为h/do=0.26.尽管楔形构型比较简单,但是该构型可以体现出级间分离中本质上的高超声速流动物理过程,而且楔形构型符合升力体外形.在本文的数值模拟中,来流攻角α=0,不同轨道级抬升角度β 下的TSTO 级间分离的静态和动态计算算例如下表1 所示,并且假设轨道级绕固定点(342,7,0) mm 动态改变抬升角度β 准备释放分离,无量纲旋转角速度为,其中U∞=2130 m/s 为自由来流速度,lb=0.432 m 为助推级模型长度.在分离的过程中轨道级在气动力矩的作用下绕重心发生旋转运动,重心以及力矩参考位置为几何质心,轨道级的无量纲质量为,惯性矩为,其中ρ∞为自由来流密度.

图1 TSTO 计算模型(单位:mm)Fig.1 TSTO computational model (unit:mm)

表1 算例设置Table 1 Simulation type of each case

1.2 来流条件

数值模拟使用的自由来流条件如下表2 所示.

表2 自由来流条件Table 2 Freestream conditions employed in the present simulations

1.3 数值方法

数值模拟采用有限体积法,通过求解可压缩理想气体Navier-Stokes (N-S) 守恒型控制方程得到TSTO 级间干扰流动.对流通量采用基于多项式插值的二阶TVD (total variation diminishing)格式对界面进行重构[30],采用Minmod 限制器抑制流场间断处的非物理震荡,并且使用HLLC (Harten-Lax-van Leer contact)近似黎曼求解器计算界面处的数值通量[31];对于黏性通量采用相同的非TVD 多项式插值方法进行计算.此外,黏性系数通过Sutherland 公式进行计算[32].不同β 下的两级间的气动干扰定常流场静态模拟采用隐式计算,并结合多重网格方法加速收敛;TSTO 级间分离动态模拟使用重叠动网格技术对N-S 方程和六自由度动力学方程耦合求解.非定常计算通过隐式双时间步长方法进行时间推进;为了捕捉到流场的物理细节变化,无量纲时间步长固定为 dt·U∞/lb=0.005 .

流场初始化采用如表2 所示的自由来流条件计算出守恒变量.对于边界条件,来流入口边界为自由来流条件;出口边界对计算域的解进行中心外推插值;壁面条件使用绝热无滑移条件.流动假设为层流流动,数值计算不使用湍流模型,因为来流雷诺数较小,而且在相关文献中研究表明,层流的数值模拟结果与风洞实验结果相近[33-34].

1.4 网格及其无关性验证

重叠网格方法被广泛用于模拟多体相对运动[35].如图2(a)所示,数值计算使用的TSTO 网格由助推级网格(背景网格)与轨道级网格组成.这两套三维计算网格基于混合网格方法生成,包含结构网格块和非结构网格块,由六面体和棱柱网格单元组成,并在不同网格块的交界处确保网格密度过渡的光滑性.在两级的壁面处采用附面层网格进行划分,壁面第一层网格高度满足y+＜ 5 用来保证较好的边界层分辨率.如图2(b)和图2(c)所示,在计算过程中,轨道级网格的外边界作为切割边界,与切割边界相交的网格单元作为切割单元,然后用其切割助推级网格中朝向轨道级网格的单元,形成助推级网格的的内边界(外边界与内边界形成两套网格的重叠区域);这样两套网格在重叠网格区域进行流场数据交换和插值,插值精度为2 阶精度;助推级和轨道级网格在重叠区域具有相近的网格单元尺度,可以避免数值解在网格重叠区域处出现由网格大小不一致引起的流场间断.由于流场与两级飞行器的动力学运动方程是耦合求解的,所以网格会同物体以相同的速度进行移动,并且在每一个时间步重新计算重叠网格连接区域,并对流场进行求解.

图2 计算网格Fig.2 Computational grid

网格无关性验证采用的3 套网格(粗糙、中等和精细网格) 单元数目分别为:500 万,1000 万和1500 万.图3 给出了TSTO 在轨道级抬升角度β=8°时这3 套网格计算得到的助推级上壁面对称线上的流向压力与摩擦力系数分布曲线.可见,粗糙网格计算结果与另外两套网格差异明显,而中等网格和精细网格的计算结果差异很小,数据差异小于0.5%,可以认为达到了网格无关性要求.所以综合考量计算效率和流场分辨率,使用中等网格用来计算和讨论TSTO 流场.

图3 网格无关性验证Fig.3 Grid independency verification

1.5 数值方法验证

1.5.1 激波/层流边界层干扰

激波/边界层干扰是TSTO 级间分离过程中非常重要的流动现象,所以这里采用文献[36]中的激波/层流边界层干扰试验结果与数值模拟结果进行对比,验证程序算法计算该问题的可靠性.试验的来流条件为Ma=2.15,Re=1.2 × 106m-1,更多的试验条件细节可以查阅文献[36].此处的数值计算依旧采用重叠网格进行计算,计算网格和流场纹影图分别如图4(a)和图4(b)所示.如图4(c)所示,数值计算出的平板流向压力P/P0与试验测量得到的数据吻合较好,可以认为采用的数值方法求解激波/边界层干扰这类复杂流动是可靠的.

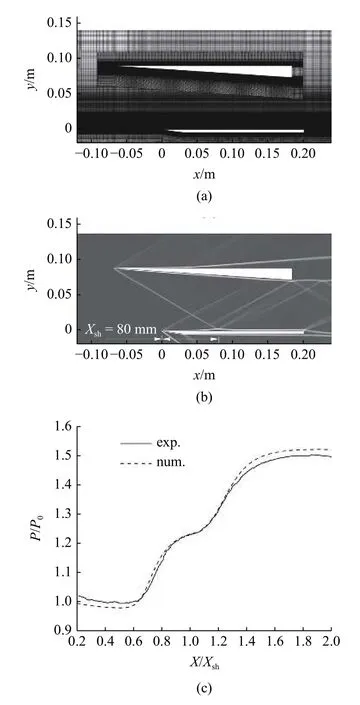
图4 激波/层流边界层干扰.(a)计算网格,(b)流场数值纹影,(c)平板流向压力数值与试验结果对比Fig.4 Shock wave/laminar boundary layer interaction.(a) Computational grid.(b) Numerical schlieren of flow field.(c) Streamwise pressure distribution of plate:comparison between numerical and experimental results

1.5.2 三维机翼/外挂物投放分离

三维机翼/外挂物投放分离试验是用来验证多体相对运动(分离)数值计算的标准案例之一[37-38].该著名的机翼/外挂物构型由美国空军实验室设计,由带有翼片的外挂物和45°前缘后掠角的半三角翼组成.机翼翼根弦长7.62 m,展长为6.6 m,渐缩比0.134.挂架安装在机翼的跨中下方位置,长度为2.29 m.外挂物长度为3.02 m,重心位置距离前端1.42 m,质量为907.8 kg,惯性矩为Ixx=27.12 kg·m2,Iyy=Izz=488.1 kg·m2.外挂物几何外形如图5(a)所示,具体的几何信息可以查阅文献[6]或文献[37].图5(b)展示了数值验证所用的混合网格(结构和非结构网格),使用重叠动网格方法对超声速飞行条件下的三维机翼/外挂物的六自由度分离运动进行无黏计算,网格总数850 万.自由来流条件为Ma=1.2,Re=7.87 × 106m-1,攻角为0°.在试验与计算过程中,在外挂物表面安装了两个喷射器用来加速外挂物与挂架的分离,抵消初始分离时刻外挂物受到的气动低头力矩.喷射器作用在外挂物上的力方向竖直向下,其中前置喷射器布置在距离外挂物头部1.24 m 处,施加作用力大小为10 679.4 N;后置喷射器布置在距离外挂物头部1.75 m,施加作用力大小为42 717.5 N,喷射器施加作用力的行程长度为0.1 m.图5 给出了外挂物在分离过程中由数值计算得到的位移与欧拉角随时间变化曲线,并与试验结果进行了对比.从图中可以看出,无黏数值计算得出的外挂物六自由度运动线位移与角位移与风洞试验结果符合程度较好,可以认为本文使用的重叠动网格求解六自由度运动具有较好的可靠性.

图5 机翼/外挂物投放分离:(a)几何模型,(b)计算网格,(c)外挂物线位移和角位移数值与试验结果对比,(d)外挂物线位移和角位移数值与试验结果对比Fig.5 Wing-poly-store separation case:(a) geometry,(b) computational grid,(c) and (d) are the linear and angular displacements of the store,respectively

2 结果与讨论

2.1 轨道级释放前流动物理及气动特性

2.1.1 分离前两级间流动物理机制

图6 给出了分别由静态和动态模拟得到的由复杂气动干扰影响最大的轨道级下壁面和助推级上壁面的空间平均压力系数随轨道级抬升角度(β)的变化曲线,由于壁面三维空间平均压力可以体现在作用在两级上的整体气动力载荷水平,所以此处选择壁面空间平均压力进行讨论.从图6 可以看出,一方面,两级壁面压力都是随着β 的增大而增大,表明两级间激波/边界层干扰导致的载荷强度逐渐增强,而且这种逐渐增强的气动干扰的强度递增速率(体现为压力系数曲线斜率)会随着β 的增大而增大,表明两级间的气动干扰随β 增加更加剧烈,流动变得更加复杂,此外轨道级受到的气动干扰要比助推级的更强;另一方面,由静态和动态模拟分别得到的壁面压力数据结果在随β 变化上没有明显的差别,二者符合程度较好.在进一步验证了动态模拟结果的准确性和可靠性的同时,可以全程表现出不同轨道级抬升角度(即β 连续变化)下两级间的流动变化细节和非定常效应.

图6 静态和动态模拟中TSTO 壁面空间平均压力随轨道级抬升角度变化曲线Fig.6 TSTO spatial average walls pressure change with the orbiter’s lifting angle (β) in static and dynamic simulation

图7 给出了不同抬升角度β 下的TSTO 的典型流场的主要流动结构以及对称面上两级壁面压力空间分布曲线.图8 给出了不同β 下TSTO 两级壁面的极限流线(摩擦力线)不同流动拓扑结构.由图7(a)和图8(a)所示,在β=0°时,助推级上壁面的边界层打在轨道级头部,由于边界层外缘流动速度为超声速,一部分流动在轨道级上壁面形成前缘激波S2,另外小部分超声速流动在下壁面形成一微弱的斜激波S3.这道弱激波在助推级上表面反射,发生激波/边界层干扰(shock wave/boundary layer interaction,SBLI),使得干扰区附近的两级壁面压力升高,并在助推级上表面形成一个小的分离区(recirculation zone).该分离区体现在助推级上壁面一个从分离鞍点S (separation saddle point) 出发的分离线(S)(separation line) 和从再附结点Na (attachment node)出发的再附线(A) (attachment line)围成的区域.由于激波/边界层干扰的强度十分微弱,所以该分离区很小,鞍点S 和结点Na 很接近,而且轨道级下壁面无类似的分离区域.由于是三维分离流动,当β=0°时该分离区在三维流动中体现为绕轨道级两侧的侧向涡,但是当β 增大后,该分离区则体现为绕轨道级两侧的马蹄涡(horseshoe vortex),并沿着分离线在三维流场向下游延伸,在尾流区与两级背面的附着涡发生干扰形成复杂的尾涡结构,并诱导产生压缩激波与尾涡发生相互作用.

图7 不同β 下TSTO 典型流场结构(左)(包含两级壁面压力云图、对称面数值纹影图、间隙内数值纹影图及压力云图以及用马赫数染色的流线图)及其对称面上壁面压力分布曲线(右)Fig.7 Typical flow structures of TSTO (left) (pressure contours of TSTO,numerical schlieren on symmetry plane,numerical schlieren and pressure contours of flow in clearance,and streamlines colored by Mach number contours) and wall pressure distribution on symmetry plane (right) in different lifting angle (β) cases

图7 不同β 下TSTO 典型流场结构(左)(包含两级壁面压力云图、对称面数值纹影图、间隙内数值纹影图及压力云图以及用马赫数染色的流线图)及其对称面上壁面压力分布曲线(右)(续)Fig.7 Typical flow structures of TSTO (left) (pressure contours of TSTO,numerical schlieren on symmetry plane,numerical schlieren and pressure contours of flow in clearance,and streamlines colored by Mach number contours) and wall pressure distribution on symmetry plane (right) in different lifting angle (β) cases (continued)

随着β 增大,TSTO 绕流流场的大致流动结构没有明显改变,只是两级间隙内的气动干扰强度增强,使得间隙出口的流动条件发生改变,两级背面后的附着涡从汇聚状态逐渐分离,并且轨道级背面尾流中的压缩激波与助推级的尾涡发生干扰.尾流中的这种压缩激波/涡干扰强度会随着β 的增加而增强,并且干扰位置会逐渐向下游移动,并会产生一道反射激波(reflected shock)与轨道级的尾涡发生相互作用,如图7(d)所示.

对于两级间隙内的流动干扰,当β 从0°增加到2°时,轨道级下方的斜激波强度稍稍增强,助推级上壁面的分离区域增大,再附结点Na 远离分离鞍点S,再附线(A)与分离线(S)之间的流通区域增大.当轨道级头部下方的入射激波S3 与助推级上壁面边界层发生干扰时,会分别产生一簇压缩波和膨胀波系,由于此时两级间距不大,所以压缩波会没有汇聚成斜激波.压缩波和膨胀波系在间隙内来回反射,直至间隙出口,可以看到助推级上壁面和轨道级下壁面的压力在间隙内的分布呈波峰对波谷依次交替的分布形状,如图7(b)所示.但是由于压缩波在轨道级上壁面引起的压升不至于使边界层发生分离,所以壁面极限流线的拓扑结构没有发生本质改变,如图8(b)所示.

当β 增大至4°时,两级间隙内的压缩波和膨胀波的反射结构转变为激波在间隙内的反射,反射激波与两级壁面边界层发生干扰.由图7(c)所示,轨道级下方的入射激波S3 打在助推级上壁面的边界层发生激波/边界层干扰,边界层流动发生分离后再附产生一道再附激波S4,S4 打在轨道级下壁面发生间隙内的第二次激波/边界层干扰.由图中的壁面压力分布曲线可以看出,间隙内的激波/边界层干扰引起了明显的压升,压力分布的趋势变化显示发生了两次激波/边界层干扰,分别在助推级上壁面和轨道级下壁面,而且引起了轨道级下壁面流动分离,在壁面上形成了分离鞍点S 和再附结点Na 的拓扑结构.由于干扰强度的增加,助推级上壁面的流动分离区增大,从图8(c)可以看到再附结点Na 的位置又向下游移动.

当β 增大至6°时,TSTO 绕流流场结构与4°情形类似,只是三维分流流动的拓扑结构发生变化.由于干扰强度的进一步增加,轨道级下壁面由于激波/边界层干扰产生的再附激波打在助推级上壁面引起了二次分离流动,助推级上壁面存在第二个分离鞍点S2 和再附结点Na2,由轨道级壁面反射的激波强度比较小,所以在助推级上壁面引起的二次分离流动区域比较小.同时可以看到助推级上壁面的再附结点Na1 位置又向下游移动,说明该分离区域不断增大,同理可见轨道级下壁面的分离区域在变大的同时还向下游移动,如图8(d)所示.

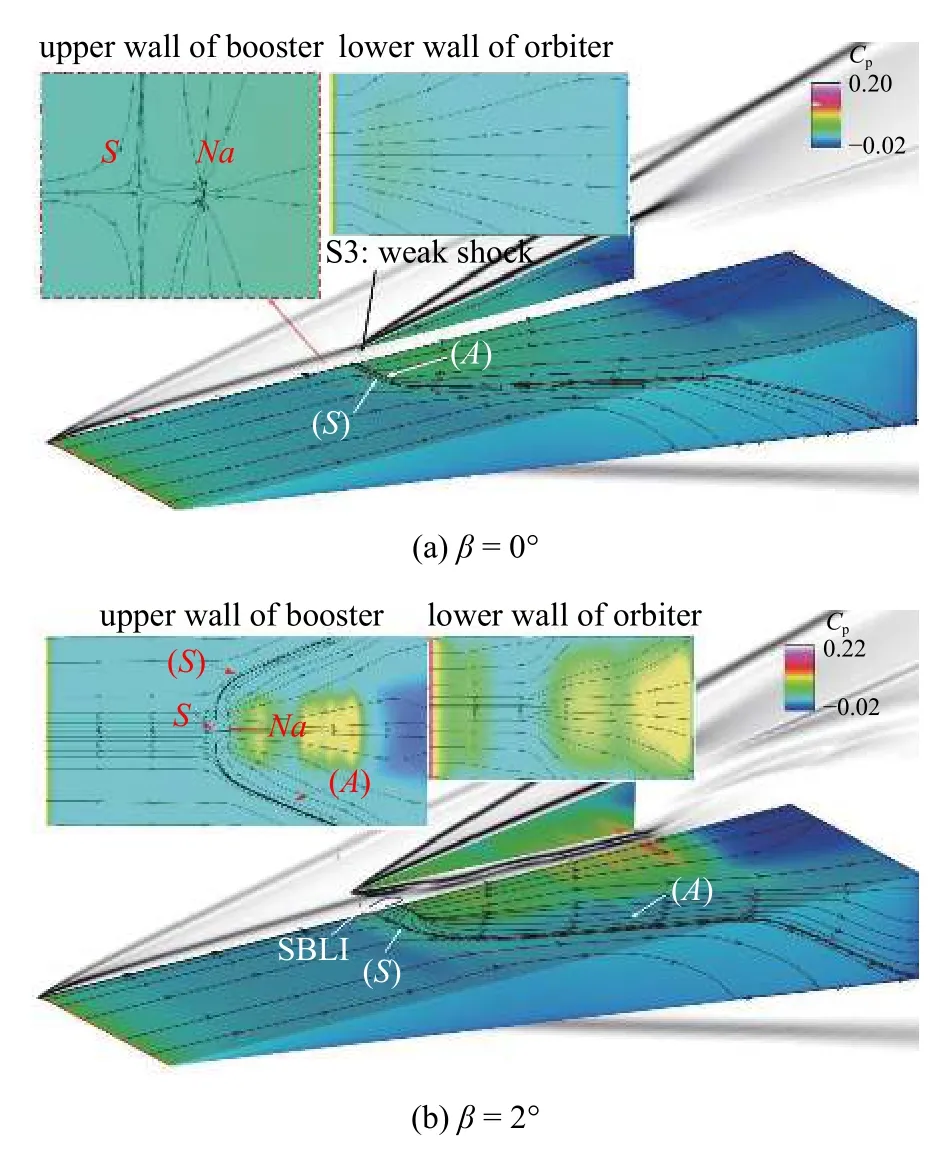
图8 不同β 下TSTO 对称面数值纹影与壁面压力空间分布及其流动拓扑结构Fig.8 Numerical schlieren and wall pressure distribution of TSTO,as well as its flow topology structure at different orbiter’s lifting angle(β) cases

在β 继续增加的过程中,虽然干扰强度增加,但是TSTO 流场结构和三维分离的流动拓扑结构都没有发生改变,但是当β 增大到12°时,两级间隙内的强气动干扰使得壁面产生了非常高的压升,间隙内的三维流动拓扑结构变得更加复杂.从图8(e)可以看出,第一个分离区域在变大的同时,分离鞍点S1向上游移动,并在再附结点Na1 下游的毗邻位置产生了一个二次分离流动区域,形成分离鞍点S2 和再附结点Na2.由助推级上壁面的二次分离流动再附过程产生的再附激波打在轨道级下壁面诱导产生分离流动(分离鞍点S1 和再附结点Na1),类似的,该分离流动再附时产生的激波打在助推级上壁面,在间隙出口附近形成三次分离流动(S3,Na3),该三次分离流动在轨道级下壁面引起其轨道级下壁面的二次分离流动,并且助推级下壁面的分离区域已经向下游移动到间隙出口附近.

2.1.2 安全分离问题讨论

在深入了解了轨道级释放前的TSTO 流场结构后,考虑到轨道级释放后的级间分离安全性,需要考察TSTO 的气动特性.图9 分别给出了静态和动态模拟中不同轨道级抬升角β 下的轨道级和助推级的气动力/矩变化曲线(对于俯仰力矩,正值表示抬头力矩,负值表示低头力矩,下同).随着β 的增大,可以看到轨道级的气动力/矩逐渐增加,这是由于两级间隙内的气动干扰逐渐增强,由于轨道级下壁面的高压区会随着β 的增大向下游移动,所以其俯仰力矩增加速率要高于气动升力.并且可以看到轨道级的升力和俯仰力矩分别在β ＜ 2°时和β ＜ 4°时小于0,说明在β ＜ 2°时肯定是不利于轨道级的分离,因为负升力和低头力矩的综合作用会使得轨道级与助推级发生碰撞.从图9(b)的助推级气动特性可以看出,随着β 的增大,助推级的气动阻力没有明显变化,说明轨道级的气动阻力对β 的变化(即气动干扰的增强)不敏感,但是助推级的气动升力会随之减小,而且由于助推级上壁面的高压区向下游的移动,其俯仰力矩也会逐渐增大.

图9 静态和动态模拟中TSTO 气动特性随轨道级抬升角度变化曲线Fig.9 TSTO aerodynamic characteristics change with the orbiter’s lifting angle (β) in static and dynamic simulation

TSTO 分离前的气动特性直接影响级间分离过程中两级的运动轨迹,决定两级能否发生碰撞.根据一般航天分离需要遵循的原则和要求[39],考虑到TSTO 级间分离的安全和可靠性,需要两级能够在预定的时间内能够正常分离,分离后不发生碰撞;两级之间不发生强干涉,分离过程对两级的气动干扰在姿态控制系统的控制能力内,飞行器不产生失稳现象;降低级间分离过程中飞行器的振动、冲击及局部变形及其可能造成的危害和影响.综合上述考虑可知,当轨道级抬升角小于4°时,两级无法安全分离,因为在未分离前轨道级受到负升力和低头力矩作用,在无额外控制力作用情况下会与助推级发生碰撞.而当轨道级抬升角大于或者等于4°时,TSTO分离的安全可靠性需要通过对级间分离过程的气动特性和分离时间等要素进一步判断,所以下一节主要对轨道级抬升角度β ≥ 4°的气动分离过程进行分析与讨论.

2.2 TSTO 级间动态分离过程分析

2.2.1 两级分离过程的动态流动物理机制

本节结合重叠动网格方法耦合求解N-S 方程组和六自由度动力方程,研究了TSTO 的气动分离以及随时间变化的气动干扰对两级气动特性的影响.假设助推级在分离过程中保持固定,轨道级零初始动量条件下释放,因为从2.1.2 节的TSTO 的气动特性来看,不同抬升角度下,助推级的气动特性变化相对于轨道级来说较小,并在分离过程中保持飞行状态尽可能不变以减少对轨道级的影响.

对于此处TSTO 级间分离来说,轨道级抬升角一般要大于4°以至于轨道级有足够大的升力利于分离,所以对初始两级夹角β=4°,6°,8°,10°,12°情况下的TSTO 级间分离分别进行了动态模拟.图10 给出了轨道级在不同初始分离两级夹角下的级间分离过程中的位移和俯仰角变化情况,其中无量纲分离时间为 t′=tU∞/lb.随着初始分离两级夹角的增加,作用在轨道级上的气动力越强,轨道级的位移越大.换言之,初始分离两级夹角越大,TSTO 级间分离所需时间越短.此外,在较大的初始两级夹角下,由于轨道级受到的气动力矩更大,俯仰角增加的更快.而且轨道级在β ＞ 6° 情况下的线位移和角位移的变化趋势和大小是相近的,这表明在这种情况下,两级间的流动结构在整个分离过程中是相似的.此外在较大的初始两级夹角下,由于轨道级受到的气动力矩更大,俯仰角增加的更快.而对于β=4°情况下的分离,从2.1 节可知,初始分离下轨道级受到较小的低头力矩压制,而且气动升力并不大,所以轨道级的分离耗时相对较长,而且俯仰角增加缓慢,这种分离情况并不理想,所以下面主要讨论以β=8°情况下的TSTO级间分离流动.

图10 级间分离过程中轨道级的位移以及俯仰角变化Fig.10 The displacement and pitching angle of the orbiter during stage separation

图11 给出了β=8°情况下级间分离过程中两级飞行器俯仰力矩系数随时间变化曲线.整个分离过程可以根据两级气动力/矩或者流场的变化分为3 个阶段:I.小间隙流动;II.大间隙流动;III.无流固干扰阶段.对于阶段I,轨道级头部未越过助推级前缘分离激波,在两级间隙内存在强气动干扰,在两级壁面上存在复杂的分离流动拓扑结构,且轨道级的气动特性快速增加.当轨道级头部刚刚越过助推级前缘激波,流场过渡到阶段II,流场主要两级壁面的激波/边界层干扰为主.当助推级前缘激波不与轨道级下壁面发生干扰时,流场过渡到阶段III,此时流场主要以两级的前缘激波与尾流中的涡相互干扰为主,而且两级之间不再发生相互干扰,级间分离完成,轨道级准备入轨.图11 中在两级俯仰力矩曲线上标注了一序列点,分别对应图12 所示的流场.下面分析TSTO 气动分离过程中的流动物理现象及其对气动力特性的影响.

图11 两级飞行器俯仰力矩系数在分离过程中随时间变化曲线(β=8°)Fig.11 Time history of the pitching moment coefficient during stage separation at the case of β=8°

图12 给出了TSTO 级间分离过程3 个阶段中5 个具有代表性的瞬时流场.在分离阶段I,两级间隙内的干扰强度随着两级间隙的增加,气动干扰强度稍微减弱,轨道级下壁面压升逐渐减小,所以轨道级受到的气动力减小.但是由于间隙的增加,入射激波S3 与助推级上壁面边界层干扰产生的再附激波S10 打在轨道级尾部的强度会逐渐减弱,并且在时刻t′=6.16,该再附激波不再与轨道级下壁面发生干扰,而且分离边界层再附过程中产生的膨胀波作用在轨道级下壁面尾部,所以轨道级尾部高压区域强度就会减小,产生的低头力矩逐渐减小并消失,而且助推级前缘激波S1 打在轨道级头部,使得头部压力升高,轨道级在这双重作用下在时刻t′=6.16 的抬头力矩在干扰阶段达到极大值.另外由于气动干扰的减弱,助推级的气动升力在阶段I 增加.

图12 β=8°情况下TSTO 级间分离过程中不同时刻流场(左:流动结构,右:对称面马赫数云图和数值纹影图)Fig.12 Flow-fields of different instants during stage separation at the case of β=8° (left:flow structure,right:Mach number contous and numerical schlieren on symmtery plane)

图12 β=8°情况下TSTO 级间分离过程中不同时刻流场(左:流动结构,右:对称面马赫数云图和数值纹影图)(续)Fig.12 Flow-fields of different instants during stage separation at the case of β=8° (left:flow structure,right:Mach number contous and numerical schlieren on symmtery plane) (continued)

对于时刻t′=8.38,入射激波S3 与助推级上壁面边界层的干扰向下游移动,由于激波/边界层干扰诱导边界层发生分离,助推级边界层分离的“拱起”诱导产生一簇压缩波系,该压缩波系与轨道级下壁面的作用随着激波/边界层干扰的位置一起向下游移动,并且助推级边界层再附过程产生的膨胀波与轨道级下壁面的作用位置也向下游移动.这两种综合作用使得轨道级下壁面压升区域从轨道级模型的重心上游移动到下游,并且尾部壁面压力减小,导致轨道级抬头力矩继续减小,同时助推级的上壁面压升也向下游移动,使得助推级抬头力矩增加,使得助推级的抬头力矩维持在一个较高的“平台”,如图11所示.另外由图12(b)所示,助推级上壁面的再附激波开始与轨道级尾流发生干扰,这种干扰引起轨道级尾涡的拉伸变形.

对于时刻t′=12.33,随着两级间隙的增加,助推级上壁面由激波/边界层干扰产生的分离高压区域进一步向下游移动,并且两级间隙内的气动干扰强度进一步减弱,轨道级下壁面不再受到助推级上壁面激波/边界层干扰的影响.另外由于助推级前缘激波打在轨道级下壁面的位置向下游移动,使得轨道级抬头力矩继续减小,而且助推级的俯仰力矩将从此刻开始明显减小.另外,再附激波S6 与轨道级尾流中的压缩激波S5 发生I 类激波干扰,产生透射激波S8,S9.

对于时刻t′=14.79,此时助推级上壁面的分离区运动到尾部末端,壁面上的再附激波S6 即将脱离并消失,所以助推级的俯仰力矩将降为未受干扰状态.由于轨道级末端不再受到气动干扰的影响,所以尾部压力分布达到最小值,而且助推级前缘激波S1 打在轨道级头部下方的位置也在向下游移动,将越过质心位置,所以此时轨道级的抬头力矩达到在阶段II 达到极小值.由于助推级上壁面再附激波S6 强度减弱,所以尾流中激波S6 与S5 的激波干扰强度减弱,轨道级尾涡变形逐渐恢复.

对于时刻t′=19.72,助推级上壁面不存在激波与边界层干扰,分离区域消失,位于助推级上壁面的马蹄涡也完全消失.微弱的助推级前缘激波S1 与轨道级入射激波S3 相交透射产生的激波S5 作用在轨道级的末端,下一刻轨道级将会完全不再受激波干扰作用影响,所以此时流场进入阶段III,此时助推级已经进入未受干扰状态,轨道级可以调整入轨姿态准备入轨,级间分离完成.另外透射激波S4 与助推级的尾流发生干扰.透射激波S5 与轨道级附着涡附近的膨胀扇发生相互作用,两级间只存在激波与尾流的干扰.

最后,从图13 级间分离过程中的壁面分离流动拓扑结构可以看出,随着两级间隙的增加,助推级上壁面的分离流动拓扑结构从一开始的双“鞍点S-结点Na”模式(见2.1.1 节)转变为单“鞍点S-结点Na”模式.而且助推级上壁面的三维分离区域(马蹄涡)逐渐向下游移动,并且分离区域逐渐减小.由于间隙内干扰强度的减弱,轨道级下壁面的压升未能产生分离流动,分离模式从一开始的“鞍点S-结点Na”很快转换为无分离模式.

图13 β=8°情况下TSTO 级间分离过程中不同时刻的对称面数值纹影图与助推级上壁面压力空间分布及其流动拓扑结构Fig.13 Numerical schlieren and wall pressure distribution of TSTO,as well as its flow topology structure of different instants during stage separation at the case of β=8°

图13 β=8°情况下TSTO 级间分离过程中不同时刻的对称面数值纹影图与助推级上壁面压力空间分布及其流动拓扑结构(续)Fig.13 Numerical schlieren and wall pressure distribution of TSTO,as well as its flow topology structure of different instants during stage separation at the case of β=8° (continued)

2.2.2 动态分离气动特性与安全分离条件分析

图14 给出了不同轨道级抬升角下的TSTO 级间分离过程中的两级气动特性变化,对应2.2.1 节中的流动物理分析.从不同的初始轨道级抬升角度下的分离过程来看,不同β 情况下气动特性变化趋势是相似的,再次说明两级间的流动结构在整个分离过程中是相似的.由于复杂的气动干扰,分离过程中两级气动力的急剧变化不是有利的,但是客观存在的.级间分离过程中的强气动干扰会给两级飞行器局部带来过高力、热载荷,可能会对飞行器产生振动以及局部变形等危害,并且其带来的过高或者过于剧烈的气动力变化在短的分离时间内不利于飞行器的稳定性控制.考虑这里两个因素,从图14 可以看出,6° ≤ β ≤ 8°情况下的TSTO 级间分离过程中的气动力变化相比于β ＞ 8°情况下的要相对平稳一些,并且两级间的气动干扰强度会小一些,不存在强干涉.从图14(b)中助推级的气动特性从分离开始到进入到阶段III 的分离时间来看,当β ≤ 10°时,随着轨道级初始抬升角的增加,完成级间分离所需的时间越短,并在β ＞ 10°时达到饱和.对于较小的轨道级抬升角比如β ＜ 6°,所需的分离时间更长,因为轨道级的气动升力不足够大,分离时间过长会增加TSTO高速分离过程中的不确定性,比如β=4°时的分离时间几乎是β=8°的两倍.综合考虑来说,轨道级抬升角在6°～ 8°可能对TSTO 级间分离具有更高的安全可靠性,在合适的较短分离时间内,两级间在不发生强干涉情况下能够平稳的安全分离,轨道级不与助推级发生碰撞,并且以合适的姿态角进行入轨.

图14 TSTO 级间分离气动特性Fig.14 Aerodynamic characteristics of TSTO during stage separation

图14 TSTO 级间分离气动特性(续)Fig.14 Aerodynamic characteristics of TSTO during stage separation(continued)

3 结论

本文对零攻角Ma=7 层流条件下的不同轨道级抬升角度β 下的TSTO 级间分离流动结合重叠网格技术分别进行了静态和动态数值研究.通过分析TSTO 壁面压力系数的变化、流场结构以及三维流动分离拓扑结构,深入探讨了两级间的气动干扰的流动物理机制,得到主要结论如下.

(1)轨道级释放前,TSTO 两级间隙内的气动干扰强度随着β 的增大而增强,并且变得更加复杂.这种复杂气动干扰伴随着两级间隙内激波/边界层干扰以及以马蹄涡为代表的三维分离结构.

(2)轨道级释放前,TSTO 三维分离流动拓扑结构随着β 的增加变得更加复杂,助推级上壁面分离区域增大,而且临界点逐渐增加(助推级上壁面分离鞍点S 和再附结点Na 对数从1 对增加到3 对,轨道级下壁面分离鞍点S 和再附结点Na 对数从0 对增加到2 对).

(3)在级间分离过程中,两级间的气动干扰强度会随着两级间隙的增加而减弱,助推级上壁面的分离区域逐渐向下游移动并减小,轨道级下壁面从初始状态的鞍点-结点分离流很快转变为无分离流动.

(4)在级间分离过程中,两级间的气动干扰强度会随着初始分离抬升角度β 的增大而增大,而且两级的气动特性变化幅度增加,分离时间会逐渐减小.根据目前数值分析结果,β 为6°～ 8°时(相对于其他轨道级抬升角度大小)可实现两级间更加安全可靠的分离.

参数列表