分部积分法的解题技巧

张磊，王利岩，吴玉斌，王辉

分部积分法的解题技巧

张磊，王利岩，吴玉斌，王辉

（沈阳航空航天大学 理学院，辽宁 沈阳 110136）

分部积分公式的作用是将积分问题化繁为简，从而达到计算目的．通过算例依次探讨了分部积分法的降幂、消去和循环作用，对照这些作用将分部积分问题分为３大类，梳理出分部积分法的使用规则．为了提高分部积分法的运算效率，对分部积分公式做了推广，借助图表生动形象地展示了求原函数的过程．通过例题分析表格法的有效性，进一步加深了学生对概念和公式的理解，提高了计算效率．

分部积分法；不定积分；图表法

不定积分算法的研究不同于极限、导数和定积分，教材中不定积分的概念通过分析语言直接给出，这种不具构造性的定义方式导致了解题方法的灵活多变．有些积分问题，用了常规方法后甚至会将被积表达式变得更复杂，以致无法计算．因此，有关不定积分计算方法和运算技巧的探究一直受到微积分学者的广泛关注．刘春平[1]介绍了含指数函数的原函数求不定积分的运算技巧，推广并证明了不定积分的链条相消法；高翔[2]讨论了被积函数为正指数次幂的指数函数与任意指数函数、正弦函数、余弦函数、双曲正弦函数、双曲余弦函数的不定积分问题，逐次分部积分后找出运算规律，用数学归纳法证得含有参数的不定积分公式；朱海[3]等梳理了部分消元法、配项与凑微分法、变量代换法和添项法等在有理函数不定积分计算中的应用，通过典型题目展示了有理函数求不定积分的常见方法与解题技巧；赵未莲[4]分析了“口诀”在微积分学习中的辅助作用，分析了不定积分计算口诀的利弊，对分部积分法的“十字口诀”进行补充，通过记忆口诀，常见的５种基本初等函数的分部积分得以解决；吴星[5]等从题目出发，结合具体算例通过观察被积函数结构梳理出求不定积分问题的思路；成凯歌[6]证明了被积函数为有限个函数乘积时不定积分的存在性及计算规律．这些研究对不定积分的常见解题方法和技巧做了进一步探究，也为多元函数积分学中的二重积分、三重积分、线面积分等问题的研究奠定了理论基础．

1 分部积分法解题规律

高等数学中，对乘积的求导公式两端取不定积分可得到分部积分公式[7]．

这些原则可以整理为分部积分口诀：反对幂三指，后者凑微分；幂角若相遇，两次同样凑．一般地，不定积分计算时最先考虑换元积分法，换元积分法不能计算时改用分部积分法．如果被积函数有三角函数或指数函数，将三角函数或指数函数凑微分，通过分部积分公式的降幂作用完成计算．如果被积函数含对数函数和反三角函数，将对数函数或反三角函数之外的函数凑微分后再用分部积分公式，利用消去作用去掉对数与反三角函数．当被积函数为指数函数乘正弦函数或指数函数乘余弦函数等形式时，可以通过2次分部积分将待求积分循环出来．

2 分部积分公式的推广

2.1 分部积分的推广公式

整理可得分部积分的推广公式

2.2 图表法计算不定积分

值得注意的是，可以通过图示将式（2）呈现给学生，方便记忆（见图1）．由此可得到计算不定积分的图表法．

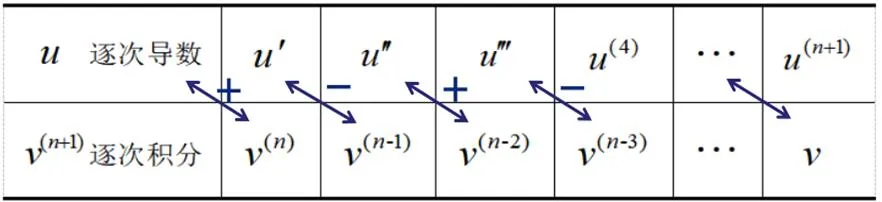
图1 分部积分推广公式递推图

Step5 填正负号：将各箭头上的2个对应项相乘后按照正负交错添写+、-号，首项为+号；

Step6 整理：将带有正负号的各项相加，写出原函数．

从图表法的解题步骤可以看出，与反复使用分部积分公式相比图表法在处理不定积分问题时可以较大程度地简化解题步骤．构造图表时如遇下述情况应停止求导或求积：（1）第１行出现0；（2）第１行的某元素再次出现或第１行某元素的常数倍再次出现；（3）箭头上两元素的乘积便于积分；（4）箭头上两元素的乘积有规律可寻．

2.2.3 图表法的优势与不足 （1）图表法的优势：通过对被积函数中的乘积因子分别进行求导运算和积分运算，学生可以借助表格清晰直观地确定原函数．尤其是被积函数中含高次多项式时，图表法可以避免前次运算结果的重复抄写，减少疏漏和笔误．另外，对于被积函数为幂函数乘幂函数、三角函数乘指数函数或原函数含抽象函数形式的不定积分问题，也可以尝试用图表法求原函数．值得注意的是，图表法不仅可以用于不定积分的计算，对定积分的计算也是有效的．图表法与积分公式法对比教学，更容易激发学生对积分的学习兴趣．（2）图表法的局限：图表法适用于部分特定类型的被积函数，为了便于迅速找到原函数，使用前需要观察被积函数的部分因子，当因子符合消去、降幂、循环作用时公式才有效．如果被积函数为对数函数乘三角函数形式或被积函数仅含反三角函数时，则无法利用图表法求解．

图2 例2解题过程演示

例2中多项式次数等于3，解题时可以利用3次分部积分对多项式函数降次以达到计算目的，但过程冗长且重复，因此选用图表法求解，将多项式函数写入第１行，借助基本求导公式对其逐次求导至0，将指数函数写入表格的第2行，借助基本积分公式逐次求积分，观察图表即可快速求解该题．

3 结语

分部积分法是积分计算的常用方法，也是本科阶段考查的重点内容．教学过程中发现，学生对公式本身掌握较好，但应用公式解决实际问题的能力有待提高．本文阐述了分部积分法在使用时的选取规则，并给出了被积函数含有多项式因子时的图表法，对照图表学生可以快速地写出不定积分结果，一定程度上提高了计算速度和准确度．

值得注意的是，在积分计算时循规蹈矩的方法有时未必是最简方法，这就要求学生在课下勤思考，多动手，熟练掌握分部积分法与基本公式法、换元积分法的综合运用．另外，后续学习过程中遇到复杂函数的不定积分时，可以借助积分表，也可以使用编程软件进行计算．并非全体初等函数都可积，且可积函数的不定积分不唯一．

[1] 刘春平．一类含指数函数的不定积分的计算[J]．高等数学研究，2020，23（6）：15-16．

[2] 高翔．一类函数的分部积分规律（一）[J]．高等数学研究，2019，22（6）：4-6．

[3] 朱海，代月红，杨晓芳．不定积分技巧探究[J]．黑龙江科学，2021（13）：66-67．

[4] 赵未莲．口诀在微积分教学中的应用举例[J]．科技风，2020（5）：61-62．

[5] 吴星，刘盼．面向问题教学的不定积分解法探究[J]．教育教学论坛，2020（26）：298-299．

[6] 成凯歌．多个函数乘积的不定积分计算[J]．高师理科学刊，2020，41（2）：13-17．

[7] 同济大学数学系．高等数学：上[M]．北京：高等教育出版社，2015．

[8] 李小斌，朱佑琳．不定积分的一个注记[J]．高等数学研究，2018，21（7）：13-15．

[9] 吴丽华．浅谈不定积分教学中的几点思考[J]．高教学刊，2019（11）：111-113．

[10] 刘琳．求不定积分几种常用方法[J]．科技经济导刊，2019（11）：141-142．

[11] 陆生琪．不定积分求解技巧解析[J]．高教学刊，2017（15）：194-196．

[12] 王玮．浅析分部积分法的运算规律[J]．课程教育研究，2019（42）：189-190．

The skills of calculating integration by parts

Zhang Lei，Wang Liyan，Wu Yubin，WANG Hui

（School of science，Shenyang Aerospace University，Shenyang 110136，China）

The function of formulas of integration by parts is to simplify the integration problem，so as to achieve the purpose of calculation．The effects of power reduction，elimination and circulation of integration by parts are discussed by examples，according to these functions，the issues on integration by parts are divided into three categories and the rules of integration by parts are sorted out．In order to improve the efficiency of integration by parts，the formula of integration by parts was extend，and the process of finding the original function was vividly shown with the help of tables．The effectiveness of the table method is analyzed through examples to deepen students' understanding of concepts and formulas and improve calculation efficiency.

integration by parts；the indefinite integral；laws of drawing

O172∶G642.0

A

10.3969/j.issn.1007-9831.2022.02.017

1007-9831（2022）02-0088-04

2021-09-18

辽宁省教育厅青年项目（L201730）；辽宁省科技厅博士启动项目（201601173）；沈阳航空航天大学教改项目（JG2020081）

张磊（1986-），女，黑龙江鸡西人，讲师，博士，从事控制论与微积分研究．E-mail：hitzhanglei@163.com