基于本征正交分解的子结构化模型降阶方法
2022-03-19张凌锋林谢昭
张凌锋,林谢昭
(福州大学机械工程及自动化学院,福建 福州 350108)
由多个组件经连接形成机械结构件是一种常见的制造手段。为获得高性能的结构件,需要应用优化设计方法来确定组件间的最优连接位置。有限元模型往往因自由度数目庞大而难以用于结构优化的多次重分析,基于响应面等“黑箱模型”方法有时也无法正确评估原系统的目标特性,因此构建具有一定精度、低计算成本的降阶模型,对系统目标函数进行快速估值,可以满足优化设计过程中计算的需要。子结构模态综合法(component mode synthesis,CMS)是构造降阶模型的有效方法之一[1-3],它将结构分割成几个由界面连接的力学上彼此独立的子结构,分别对子结构进行模态分析获得降阶基,然后通过子结构边界上的力和位移等协调条件,拼装组成系统级的降价模型(reduced order model,ROM)。一般来讲,保留其低阶模态即可满足工程求解精度的要求。目前,虽然已经开发了许多CMS技术,但它们本质上并不是为了复杂结构的优化设计而构造的,因为当整体结构中某些组件参数发生变化时,ROM无法轻易地被重新构造。
在动力学领域,还可通过对系统的响应(样本数据)进行本征正交分解(proper orthogonal decomposition,POD)[4],获得本征正交模态(proper orthogonal models,POMs)来构造缩减基集合。POD能将大量相互依赖的变量缩减成少数几个不相关的变量,即POMs,同时尽可能多地保持在原变量中所具有的变化,这样就能用较少的基数目来精确地表示结构动态特性。POD法提供了一种研究线性和非线性力学系统的替代方法。Steindal等[5]认为,在Galerkin方法中,POMs是构造降阶基的最好选择。在系统质量矩阵与单位矩阵成比例的情况下,POMs严格地收敛于模态振型[6]。尉飞等[7]利用POMs代替线性特征模态,得到一种能解决具有局部非线性问题的降阶模型;Confalonieri和Liang等[8-10]利用POD对耦合系统中的各物理域进行降阶处理,以适应多场耦合的系统仿真分析;Wang等[11]将POD方法与子结构综合法结合用于复杂结构件的模态分析,以此来精确预测结构中某一组件的动力响应,从而避免了对结构的整体分析;王小娟等[12]提出了一种POD结合平衡截断方法的模型降阶技术。因此,可以尝试将POD用于构造能适应结构优化设计参数变化的降阶模型,当结构参数在一定范围内发生改变时,POMs就不需要重新构造而具有足够的计算精度[13]。
本文将Craig-Bampton(CB)方法与POD结合,由POD确定需要修改的子结构本征特性,通过组件的POMs获得子结构的降阶变换矩阵,结合动态子结构装配技术,从而获得系统级的降阶模型(ROM),当子结构组件参数发生改变时,无需使用完整的修改后的动力学方程组进行昂贵的重分析。通过算例验证了该ROM在不同载荷、不同板厚时的快速重分析能力。
1 PCB-ROM的构造
POD结合CB方法构造降阶模型,是围绕着子结构组件进行的。对于参数发生变化的子结构,采用POD模态(POMs)作为缩减基;对于参数未改变的子结构组件,则仍采用CB主模态构造其低阶模态基。获得各个子结构组件动态特性的降阶表达之后,根据各子结构间的边界协调条件,进行模态综合,获得整体结构的降阶模型(PCB-ROM)。
以图1所示的简单平板结构件为例,将其分割为a、b两个子结构,子结构的坐标分割为界面坐标xj和非界面坐标xi,则子结构的无阻尼运动学方程为:
(1)
对应的组件边界界面条件:
xaj=xbj
(2)
faj+fbj=0
(3)
式中:m,k分别为子结构的质量矩阵和刚度矩阵;f为子结构界面力;g为作用于子结构的外力。
假设子结构a的参数发生变化,则POMs坐标变换矩阵为:
(4)

求解POMs的具体计算过程如下:首先通过静力有限元分析获得整体结构的节点位移矩阵,然后分解得到子结构的内部节点位移,并存储到位移快照矩阵X中:
(5)
式中:n为子结构内部节点自由度;k为取样次数。
将快照矩阵去均值处理后,获得系统的相关矩阵R:
R=VVT
(6)

(7)

子结构的POMs坐标变换矩阵为:
(8)

将a、b两个子结构经过坐标变换后的方程“堆积”起来,可得:
(9)
由位移、界面力协调条件可得到第二次坐标变换为:
(10)
式中:B为布尔矩阵;q为广义坐标。
将式(10)代入式(9),可得到降阶后系统的运动方程为:
(11)

式(11)即为PCB-ROM模型的表达式。对于多个组件连接成的复杂结构而言,可以采用上述POD结合CB的方式构建降阶模型。
2 算例验证
以U型板件为例,边界条件以及载荷情况如图2所示。弹性模量E=2.1×1011N/m3,密度ρ=7.9×103kg/m3,泊松比μ=0.3,板厚为t=50 mm(薄板结构)。在ABAQUS中采用壳单元建立有限元模型(FEM),单元数为1 400,节点数为1 491个,总自由度数为8 946。其中,子结构S1和S4所划分网格均为15×20,节点数为336(内部节点数315,界面节点数21),自由度数为2 016;子结构S2和S3所划分网格均为20×20,节点数为441(内部节点数399,界面节点数2×21),自由度数为2 646。
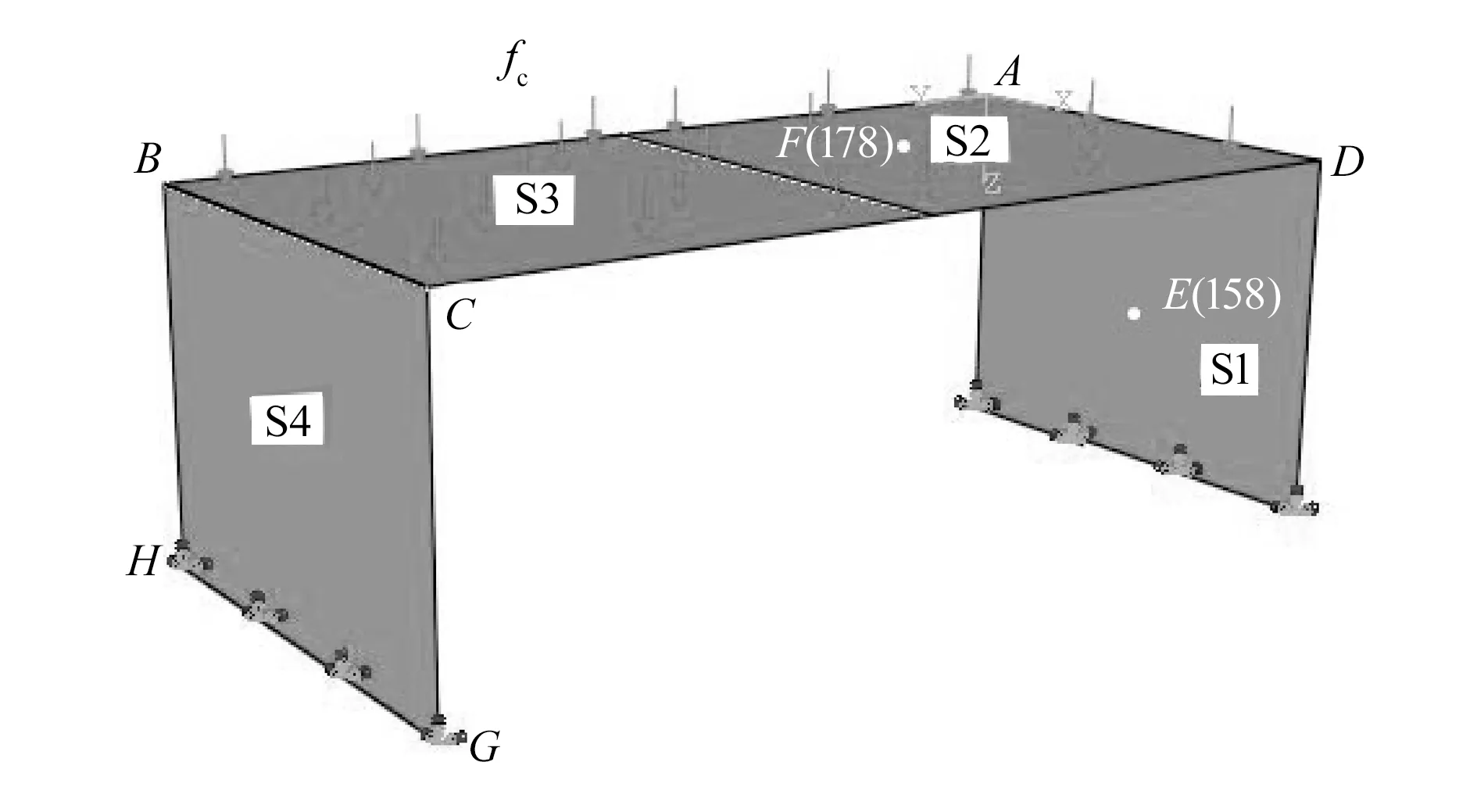
图2 U型连接板
假设U型板件中子结构S1、S3发生变化,而子结构S2、S4没有发生改变。利用1节中所描述的POD结合CB的方法构造U型板的ROM(记为PCB-ROM)时,通过求解子结构S1、S3的POMs构造S1、S3的低阶模态,利用CB方法构造S2、S4的低阶模态。对不同大小的面载荷fc,分别提取子结构S1和S3的位移,共得到6组位移快照矩阵。由POD能量比原则可知,选取m=1阶POMs即可满足所选的基向量所含“能量”占总基模态“能量”99.99%的要求。对于子结构S2和S4,采用保留主模态作为缩减基函数构造子结构降阶模型,考虑结构20 Hz内的固有频率,由主模态截断标准得到的保留主模态数也为1。因此,PCB-ROM的自由度数为382,其中子结构内部的自由度数为4,界面的自由度数为378。
利用传统的CB方法构造该U型板件的ROM(记为CB-ROM),同样如果考虑结构20 Hz内的固有频率,4个子结构要保留的主模态数均为1,则CB-ROM的自由度为382,其中子结构内部自由度数为4,界面自由度数为378。
2.1 PCB-ROM与CB-ROM的比较
表1给出了上述3种模型的自由度数和结构频率重分析的计算时间。由表1可知, PCB-ROM的重分析效率比CB-ROM提高了约10倍,大幅度降低了重分析的计算成本。

表1 FEM与PCB-ROM以及CB-ROM的比较
计算精度方面,这里先给出PCB-ROM、CB-ROM与FEM(作为标杆)分别计算得到的低阶频率结果对比,如图3所示。结果表明, 虽然PCB-ROM的计算误差大于CB-ROM,但PCB-ROM计算的前两阶固有频率的误差均小于1%,仍具有足够的计算精度。

图3 PCB-ROM和CB-ROM的低阶固有频率及相对于FEM结果的误差
计算结构的静态变形时,假设U型板子结构S2、S3上所施加的面载荷fc=3 kN,3种模型计算得到的静变形结果如图4和图5所示。考虑到模型的对称性,这里只给出子结构S3和S4的静变形结果。由3种模型计算得到的结构件CD边上节点的位移比较结果如图6所示。由图可知,由PCB-ROM和CB-ROM计算的静变形位移响应曲线与FEM曲线吻合度良好,说明PCB-ROM与CB-ROM都具有很好的复现全自由度模型结果的能力。

图4 子结构3的静态变形结果比较

图5 子结构4的静态变形结果比较

图6 PCB-ROM、CB-ROM和FEM计算得到的CD边处位移响应结果对比


图7 简谐载荷激励下,PCB-ROM、CB-ROM与FEM计算得到的E、F点的位移响应曲线
综上所述,本文所提出的PCB-ROM能够以较高的计算精度和较低的计算成本,很好地表达原始模型的特性,能够代替原FEM模型,满足工程上的重分析需求。相较于传统的CB-ROM, PCB-ROM有着高得多的计算效率。
2.2 PCB-ROM对子结构参数变化的适应性研究
为验证PCB-ROM能够应用于多组件连接结构件的优化设计中,需要考查当子结构设计参数发生变化时,PCB-ROM的快速重分析能力。以对称结构U型板为例,取3种不同的S1、S3板厚t1和t3组合:1)t1=40 mm,t3=50 mm;2)t1=40 mm,t3=60 mm;3)t1=50 mm,t3=60 mm。利用PCB-ROM求解这3种不同板厚组合结构的第一、二阶频率,并与FEM的计算结果进行比较,结果见表2。由表2可知,PCB-ROM与FEM模型计算的第一、二阶频率相吻合,满足工程精度要求。

表2 PCB-ROM与FEM计算的第一、二阶频率结果的比较
求解上述相同简谐载荷激励下U型板的响应。利用PCB-ROM和FEM分别计算0~20 Hz频段内不同板厚组合下U型板结构的位移响应,频率步长为0.01 Hz,受限于篇幅,这里仅仅给出结构上挠度值较大的F点(子结构2内节点编号为178)的位移响应曲线,如图8所示。结果表明,二者的计算结果相吻合,即当板厚在一定范围内变化时,原来构造的PCB-ROM能够很好地近似表述板厚变化后结构的静动态特性,无需重构板厚变化后结构的ROM。说明PCB-ROM对不同的板厚变化具有良好的适用性,可以将其用于优化设计。

图8 简谐激励下,不同板厚组合下PCB-ROM与FEM的F点处的响应结果对比
3 结束语
本文提出用POD来构造需要修改的子结构的缩减基,结合动态子结构装配技术获得系统级的降阶模型。对结构的固有频率、静变形以及谐振载荷激励下的动态响应等的计算结果表明,PCB-ROM能替代原结构的FEM模型,实现结构的快速重分析。与传统的CB-ROM相比,PCB-ROM能够利用POVs清楚地指示POMs的贡献程度,且建模及分析计算的效率得到很大程度的提高。在不同载荷、不同子结构板厚组合的情况下,PCB-ROM都具有良好的计算精度和适用性,能够正确地反映结构组件由于参数变化而导致的特性改变。因此,POD-CB降阶方法可替代复杂的FEM,用于组合机床、液压机底座等多组件复杂结构动力特性的优化设计中。
