基于Kahan方法的磁流变抛光凸元件几何特性分析

杨 航,佘 娜,张云飞,黄 文,贾 阳

(1.遵义师范学院工学院,贵州 遵义,563006；2.中国工程物理研究院 机械制造工艺研究所,四川 绵阳,621900；3.华中光电技术研究所 武汉光电国家实验室,湖北 武汉,430073)

1 引 言

空间光学、天文光学、惯性约束聚变以及紫外光刻等高技术领域对光学系统的要求不断提高[1-2]。光学元件在以后的航空、国防、宇宙探索、核聚变等诸多邻域都将起到越来越重要的作用,高精度的光学零件与高要求压力场的光学元件对于某些领域更是具有不可替代的作用。为了一些光学元件的表面的精度、表面的质量以及表面压力场都能满足需要的条件[3-4],世界上许多国家对光学元件的表面进行了大量的研究,并找寻加工的方法,这些方法中包括了离子束加工、在线电解修整磨削拋光、Teflon法抛光、磁流变抛光(MRF)等[5-6],但是因为其研究的工作还不够,有些技术不是很完善。在这些技术中,MRF技术是利用了抛光液在磁场中形成一段凸起的“柔性缎带”[7-8],通过“柔性缎带”在加工工件表面进行抛光[9-10],为可控的柔性抛光技术[11]。MRF是用来获得超高精度光学表面的技术,运用磁流变抛光技术加工光学元件将变得越来越广泛。对于磁流变抛光区域压力的研究,董敏运用磁流变抛光技术对微结构动压平面进行了研究[12]。对于一些压力场控制严格的凸光学元件,特别是对于航空、航天、激光核聚变等领域对凸光学元件的压力场控制极为严格时,磁流变抛光区域的压力场就变得极为重要。总的来说,磁流变抛光压力场的实验获取方法存在三方面的困难:(1)因为流场尺度小,与设备属于同一量级,不论是点式还是薄膜式的传感器介入都会引起磁流变抛光区域压力场畸变,导致测得的数据精度丧失或失效；(2)传感器对压力场的测定成本居高不下,且不能够获得实时、动态、多参数耦合流场；(3)目前基于牛顿法、荣格库塔方法开展的数值计算由于受到多因素、多场耦合产生的非线性积分特性,计算效率低下甚至无法计算。面向这些问题,本文提出基于Kahan方法的快速数值计算,使高效率磁流变抛光区域流场几何特性获取成为可能。

2 凸光学元件与磁流变抛光区域压力分析

2.1 磁流变抛光过程

磁流变抛光是指被加工工件(本文所研究的凸光学元件)放置在一个运动抛光轮上方,加工工件与抛光轮的上部会形成一个很小的距离,使加工工件便于在运动的抛光轮上部形成一个很小的间隙,如图1所示。

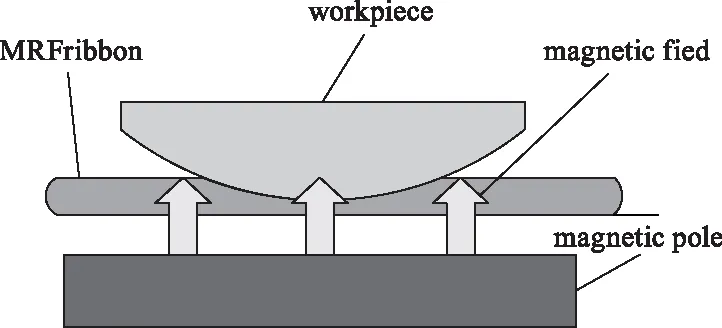
图1 磁流变抛光加工凸光学元件的示意图

在运动的抛光轮下方布置一电磁铁磁极,与加工工件相互对应,就会在加工工件与抛光轮的小间隙附近产生一个非均匀的磁场。当磁流变抛光液随着抛光轮运动到加工工件与抛光轮形成的小间隙的附近时,以附着在抛光轮上流动的磁流变液转变成一段凸起的“柔性缎带”,抛光液受力凝聚、变硬,成为粘度很大的类似Bingham质的流变液。当这样具有较高粘度的“柔性缎带”Bingham介质进入狭小间隙时,抛光液会与加工工件相接触,使介质对光学元件表面所相接触的区域会产生一定的剪切作用,进而把光学元件表面区域的部分材料去除,达到微量去除的目的,在加工工件的表面与抛光液相互接触并被去除材料的部分被称为抛光区。

2.2 凸光学元件曲率分析

本文研究凸光学元件曲率对磁流变抛光区域压力场的影响,图2为磁流变抛光过程中,磁流变液的中平面下凸光学元件与抛光液形成的抛光区在XOY坐标下的参数,定义抛光区任意一点为Q,Q点与凸光学元件顶点的距离为h(m),x为该点在X坐标轴上的坐标值。

图2 XOY坐标示意图

从图中可以得到关于x的方程,其表达式如下:

x2=R2-(R-h)2=2Rh-h2

(1)

式中,R为凸光学元件的半径,由公式可知x是关于R的函数。

考虑到影响x的不止凸光学曲率,还有光学元件的嵌入深度,而嵌入的深度又与嵌入的角度相关,所以本文主要研究影响压力的主要因素有光学元件的曲率R、光学元件在磁流变液中的浸入深度L、光学元件浸入磁流变液的角度A三个方面。

2.3 凸元件与磁流变液压力场的形成

磁流变抛光的数学模型是以Preston方程为依据所建立的。凸光学元件抛光时,磁流变抛光液对于加工工件的压力P是由许多方面的因数来影响的参数,但它主要由两个部分组成:即磁场所产生的压力和流体动压力。其中流体动压力,是在无滑动的边界条件、恒定粘度和可忽略的物体作用力的假设条件下由Reynolds方程所解出；磁场产生的压力也包括两部分:磁化压力和磁致伸缩压力,但由于本文所研究的磁流变抛光液在流动过程中近似为不可压缩流体,在梯度磁场中,随着体积的变化,磁流变抛光液的磁致伸缩压力可以近似为零,所以只考虑磁化压力。则有:

(2)

式中,η0为抛光液粘度；h0为Q点在Y轴上的长度；Ux为抛光轮转速；μ0在真空下的磁导率；Mf为磁流变抛光液的磁化强度；H是在外加磁场的磁场强度。其中磁场强度的表达式为:

(3)

式中,h1为磁极到工件的最小距离。

由式(2)与(3)压力是关于x的函数,再根据2.2小节得到的结论,可知压力与光学元件的曲率R、光学元件在磁流变液中的浸入深度L、光学元件浸入磁流变液的角度A三个方面有关。

3 基于Kahan线性化的多场耦合积分的快速计算方法

3.1 Kahan线性化原理

对于一般形式的微分方程组:

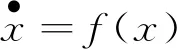
(4)

其中:

f(x)≜A(x)+B(x)+C

(5)

式中,A、B、C分别为n维二次型矩阵、n维方阵、n维列矩阵。采用固定点中心迭代,有:

xt+1=xt+s[A(xt+1,xt)+B(xt+1,xt)+C(xt+1,xt)]

(6)

其中,t为迭代步次；s为步长。有:

(7)

显然,该积分方法是对称和线性隐式的。

3.2 压力场多因素耦合快速计算方法

对于式可以看作具有一般形式:

p≜f(Ux,h,x,M,R,μ0,η0)

(8)

因此,按照式(6)开展数值积分计算,可以将多物理场、多因素耦合的非线性微分方程转化为线性隐式方程进行求解。对多因素的独立调控并不影响单次积分的迭代总时间。在时间效率上有极大的优势。这是开展几何特性多工艺因素分析的基础。

4 凸元件几何特性计算

4.1 实验设计

为了研究在磁流变抛光过程中磁流变抛光区域的压力场,除了本文主要研究的凸光学元件的曲率、嵌入深度与嵌入角度以外,其影响该过程的工艺参数还有很多,如磁流变抛光液入口的运动速度、压强以及抛光液参数等。

由于磁流变液在附加磁场的作用下,磁流变液转变成一段凸起的“柔性缎带”,抛光液受力凝聚、变硬,形成具有一定屈服应力的类固体。考虑到流动状态磁流变抛光液的流动特征,流体模型选取的是k-epsilon的湍流模型,由于磁流变液在梯度磁场下成为粘度很大的类似Bingham介质的磁流变液可以近似由Herschel-Bulkley模型来代替,所以可采取Herschel-Bulkley模型参数进行试验。具体磁流变液各关键参数如表1。

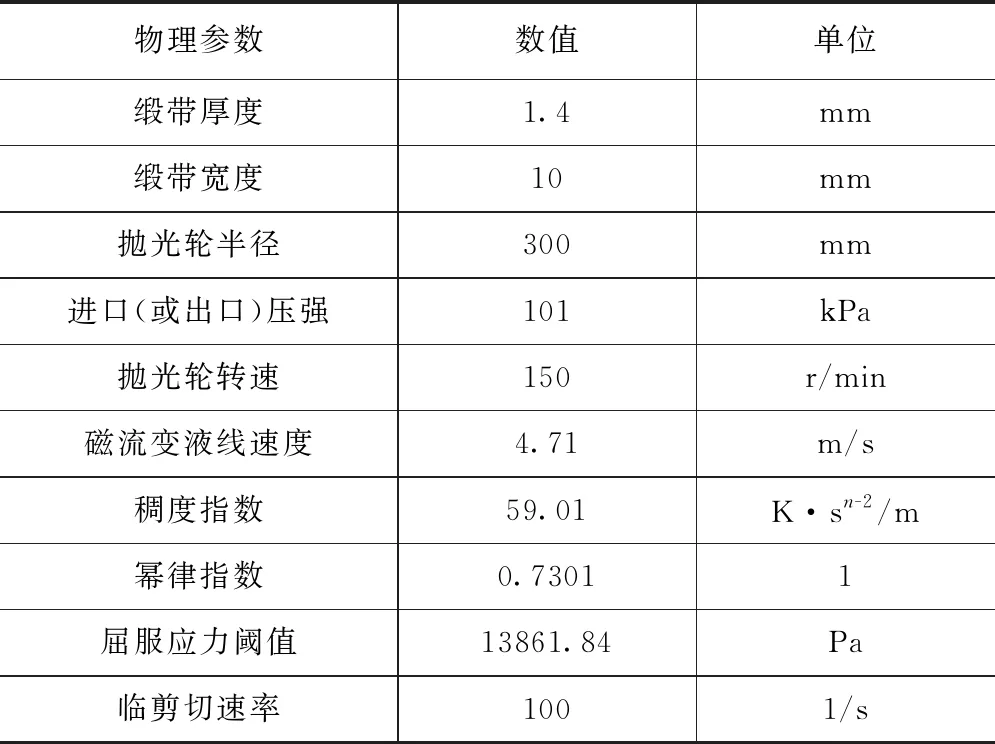
表1 选取的磁流变抛光各参数

确定了以上参数进行分析时,共分为三组实验:

(1)第一组实验是以抛)轮转速150 r/min、嵌入深度为1 mm、嵌入角度为0°作定值,改变凸光学元件的曲率的情况下来分析磁流变抛光区域的压力场,具体参数如表2所示。

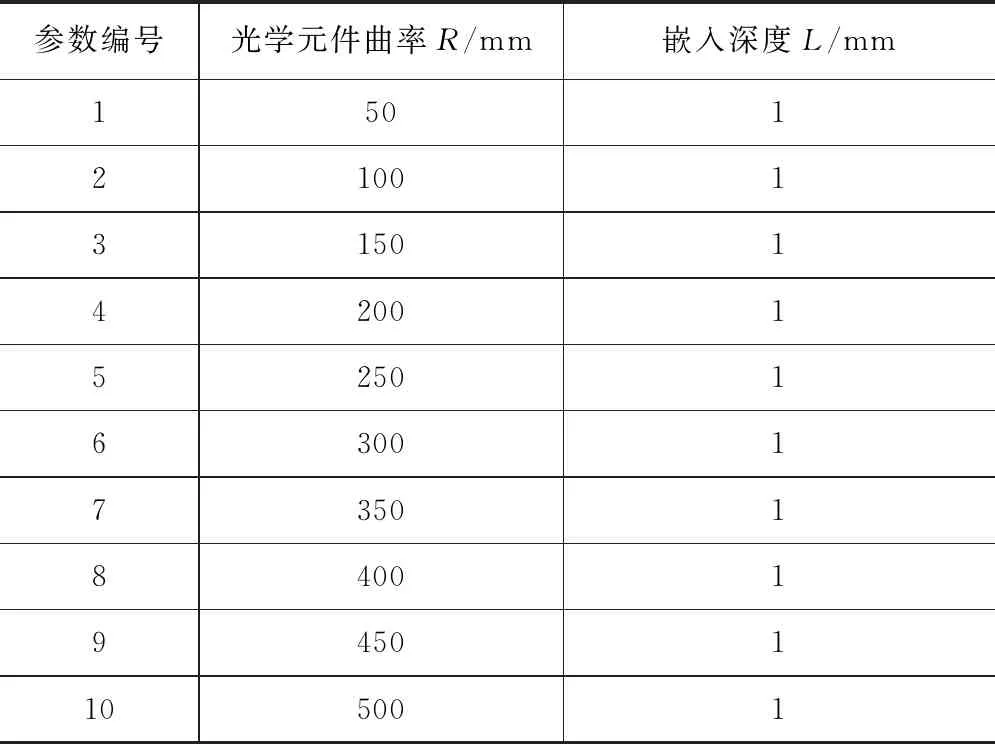
表2 光学元件曲率在50 mm至500 mm的实验参数

(2)第二组实验是以抛)轮转速150 r/min、凸光学元件曲率为200 mm、嵌入角度为0作定值,改变凸光学元件的嵌入深度的情况下来分析磁流变抛光区域的压力场,具体参数如表3所示。

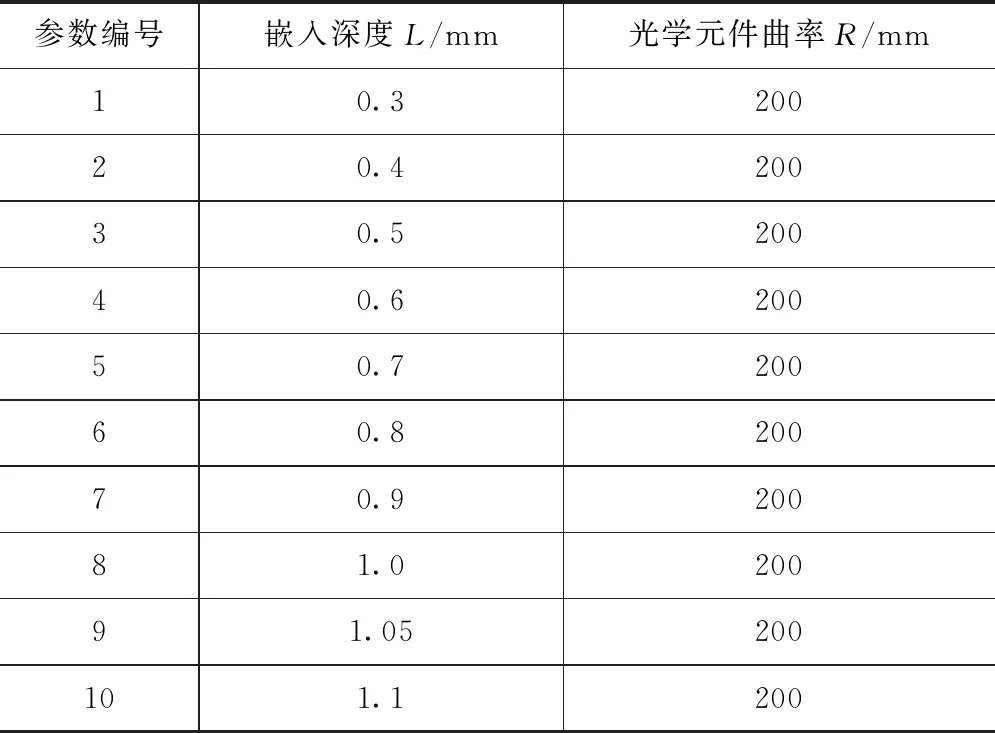
表3 嵌入深度在0.3 mm至1.1 mm的实验参数

(3)第三组实验是以抛)轮转速150 r/min、凸光学元件曲率为200 mm、嵌入深度为1 mm作定值,改变凸光学元件的嵌入角度的情况下来分析磁流变抛光区域的压力场,具体参数如表4所示。

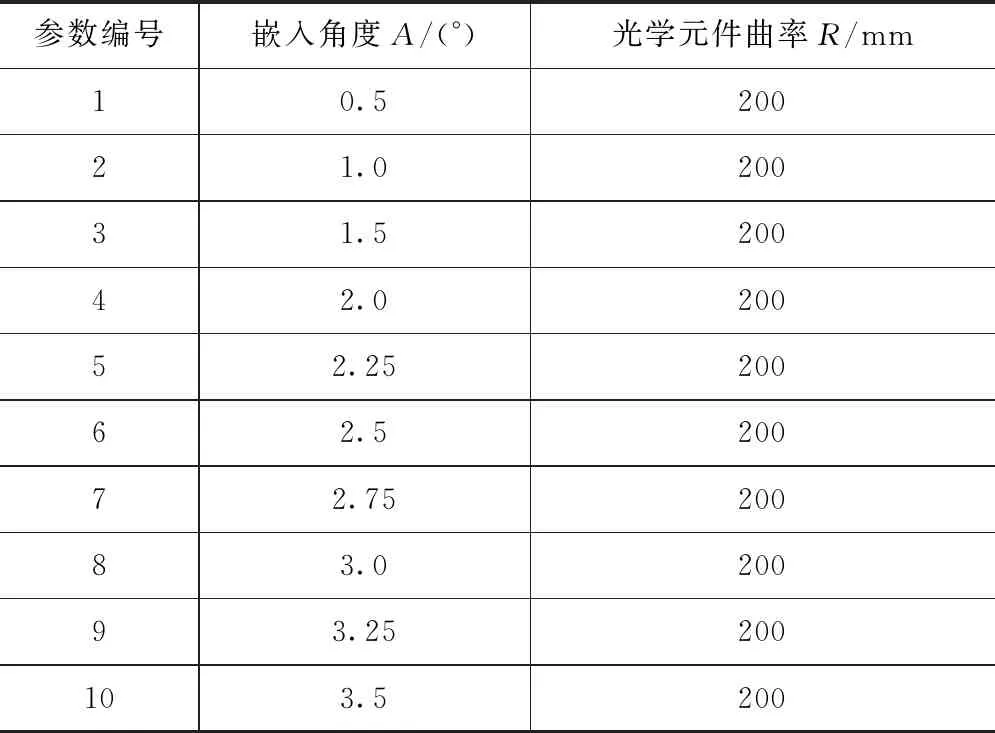
表4 光学元件嵌入角度在0.5°至3.5°之间的实验参数

4.2 凸元件曲率对凸面的压力影响

在磁流变抛光的过程中,由于凸光学元件的曲率的不同会对抛光区域内磁流变抛光液的压力产生变化,以嵌入深度为1 mm与嵌入角度为0°作定值,凸光学元件不同的曲率作为研究对象,图3为不同曲率时仿真实验所得出的对磁流变抛光区域压力对应的结果。

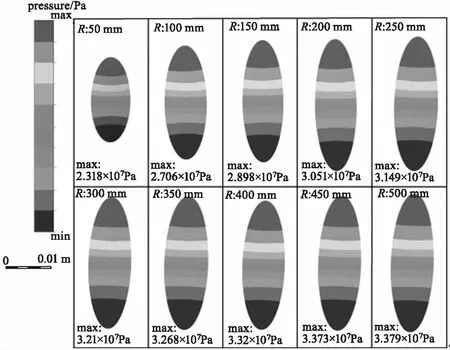
图3 曲率在50 mm至500 mm的磁流变抛光区域压力分布图

由曲率在50 mm至500 mm经过计算到数据,得到在磁流变抛光区域中凸光学元件曲率不同时,抛光液的压力分布曲线图,如图4。

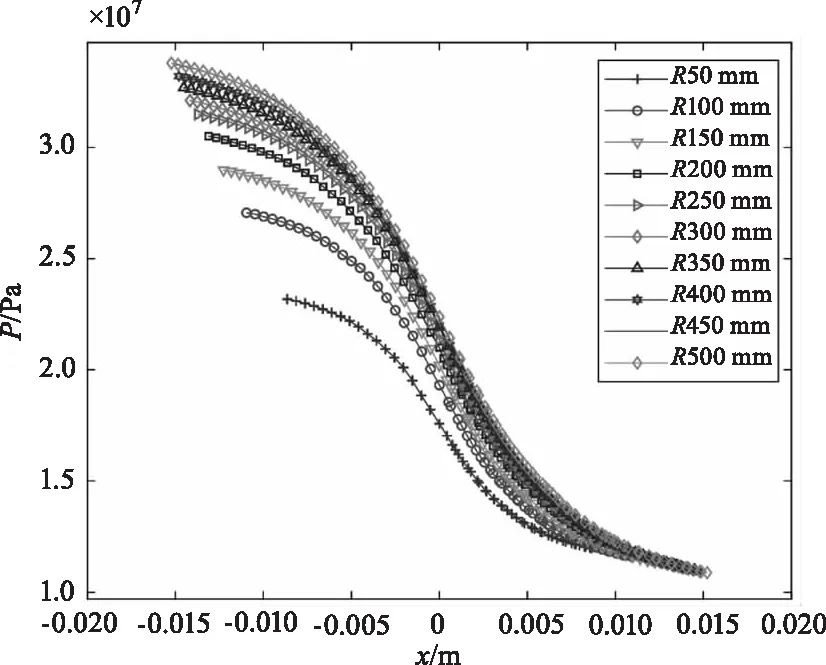
图4 凸光学元件曲率在50 mm至500 mm的压力分布曲线图

从图4中可以看出,凸光学元件曲率对磁流变抛光区域压力的影响具有规律,由单个曲线可知,磁流变抛光区域中磁流变抛光液进入凸光学元件的x不断增加,其压力减小；这与工程经验一致,浸入长度出口方向存在较高的压力梯度,边缘部分存在急剧的压力泄露现象。这也是磁流变抛光边缘部分难以去除的原因。并由图4可知,抛光液进入光学元件的前段压力缓慢减小,中段压力减小较快,后段压力缓慢减小。由图4中不同曲率压力曲线的变化可知,磁流变抛光区域中凸光学元件的曲率不断增加,其压力不断增大；在抛光区域中抛光液进入凸光学元件的前段时,凸光学元件曲率的增加使压力增大更为显著；在后段时变化微小,特别是在磁流变抛光液与凸光学元件出口的位置,凸光学元件曲率越大压力反而较小。

4.3 相同曲率下凸元件嵌入深度对凸面的压力影响

在磁流变抛光过程中,由于凸光学元件嵌入深度的不同会对抛光区域压力产生变化,以凸光学元件曲率为200 mm与嵌入角度0°为定值,以不同的嵌入深度作为研究对象,图5是不同的嵌入深度下计算出的对磁流变抛光区域压力分布图。

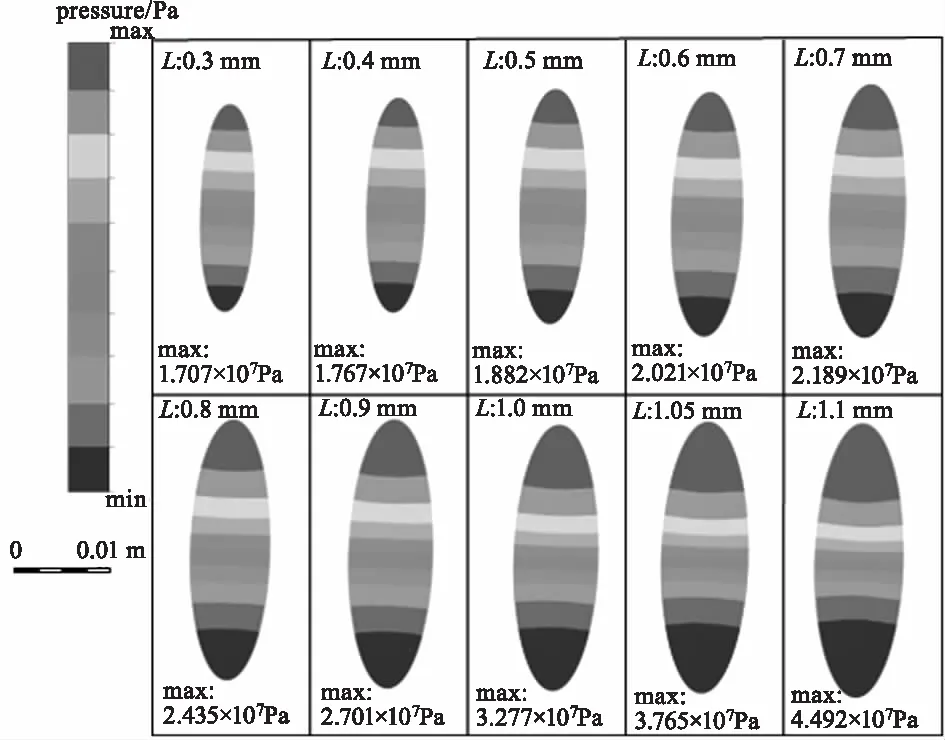
图5 嵌入深度在0.3 mm至1.1 mm的磁流变抛光区域压力分布图

由嵌入深度在0.3～1.1 mm下经过计算得到数据,得到在磁流变抛光区域中凸光学元件嵌入深度不同时,抛光液进入的压力分布曲线图,如图6。

由图6可知,当深度一定时,磁流变抛光区域中磁流变抛光液进入凸光学元件的位移不断增加,其压力减小；抛光液进入凸光学元件的前段压力缓慢减小,中段压力减小较快,后段压力缓慢减小。由图6中不同深度曲线的变化可知,磁流变抛光区域中凸光学元件的嵌入深度不断增大,其压力不断增加；当嵌入深度越小时,抛光液进入凸光学元件的位移压力曲线越平缓,即变化速率越小；当嵌入深度越大时,抛光区域的压力曲线越陡峭,即变化速率越大；当抛光液进入凸光学元件前段时,凸光学元件嵌入深度的增大使压力增加更为显著,在后段时变化微小,特别是在磁流变抛光液与凸光学元件出口的位置,图中所有线合为一点,即凸光学元件嵌入深度改变时其压力不变。这也就揭示了抛光过程入口区域与出口区域压力场变化的不一致性,出口区域梯度较高,对于不同曲率条件并不能产生明显的压力差异。而入口区域由于有较长的压力接触区,因此能够明显看到压力的变化。

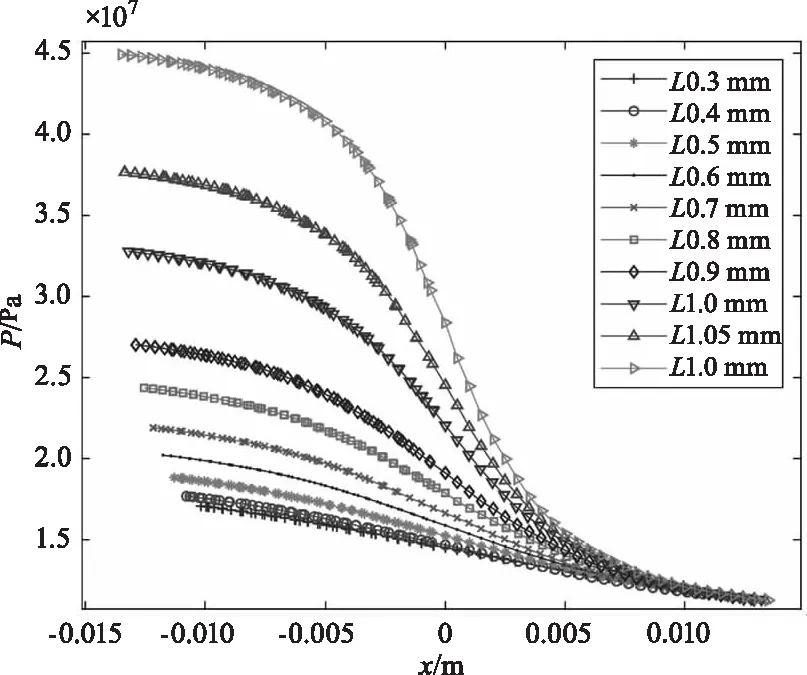
图6 凸光学元件嵌入深度在0.3 mm至1.1 mm的压力分布曲线图

4.4 相同曲率下凸元件嵌入角度对凸面的压力影响

在磁流变抛光过程中,由于凸光学元件的嵌入角度的不同会对抛光区域产生影响,以凸光学元件曲率为200 mm与嵌入深度为1 mm为定值,不同的嵌入角度作为研究对象,图7是不同的嵌入角度时计算所得出的抛光区域压力分布图。

图7 嵌入角度在0.5°至3.5°的磁流变抛光区域压力分布图

由嵌入角度在0.5°～3.5°的计算得到数据,得到在磁流变抛光区域中凸光学元件嵌入角度不同时,抛光液进入的压力分布曲线图,如图8。

由图8可知,当角度一定时,当磁流变抛光液进入凸光学元件的位移不断增加,前段压力缓慢减小,中段压力减小较快,后段压力缓慢减小。受到压力场形成机制的影响,前端与后端出现明显的压力角度响应机制。由图8中不同嵌入角度的变化曲线图可知,磁流变抛光区域中凸光学元件的嵌入角度越小,其位移压力曲线图越平缓,即压力减小速率越慢；凸光学元件的嵌入角度越大,其位移压力曲线图越陡峭,即压力减小速率越快；当磁流变抛光液进入凸光学元件前段时,磁流变抛光区域中凸光学元件的嵌入角度不断增大,其压力不断增加；在抛光液进入凸光学元件最深点附近,也就是凸光学元件的顶点位置(X轴的0点位置)靠左段,抛光区域压力曲线相交,即压力趋于相等；当磁流变抛光区域中抛光液进入凸光学元件后半段时,磁流变抛光区域中凸光学元件的嵌入角度不断增大,其压力不断减小,最终在磁流变抛光液与凸光学元件出口的位置,图中所有线合为一点,即凸光学元件嵌入角度改变时其压力不变。

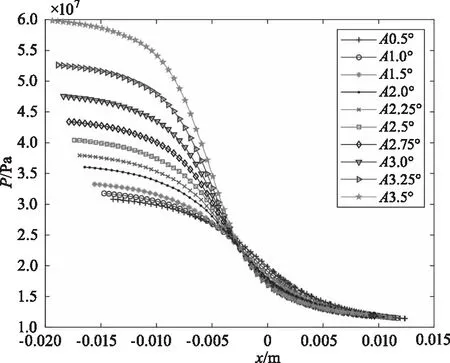
图8 凸光学元件嵌入角度在0.5°～3.5°的压力分布曲线图

5 结 论

本文依赖于Kahan方法对变抛光区域压力场进行快速多因素耦合计算研光学元件几何特性对磁流变液抛光区域压力场影响机制的问题。该方法较为方便的处理多场耦合计算问题。主要结论如下:

(1)无论凸光学元件曲率、嵌入深度、嵌入角度怎么变化,磁流变抛光区域中磁流变抛光液进入凸光学元件的位移不断增加,其压力减小。

(2)基于嵌入深度10 mm为定值,凸光学元件曲率在50 mm至500 mm的变化下对磁流变抛光区域压力的研究,当抛光区域中凸光学元件的曲率不断增大,其压力不断增加；当抛光液进入凸光学元件的不同位移下,位移较小时压力变化显著,压力随曲率的增大而增加；当位移较大时压力变化变化微小,特别是在磁流变抛光液与凸光学元件出口的位置,凸光学元件曲率越大压力反而较小。

(3)基于曲率200 mm为定值,凸光学元件嵌入深度在0.3 mm至1.1 mm的变化下对磁流变抛光区域压力的研究,当抛光区域中凸光学元件的嵌入深度不断加大,其压力不断增加；当嵌入深度越小时,压力的变化速率越小；当抛光液进入凸光学元件的不同位移下,随嵌入深度的增大；当位移较小时压力变化显著,位移较大时压力变化趋于零。

(4)基于曲率200 mm与嵌入深度1 mm为定值,凸光学元件嵌入角度在0.5°至3.5°的变化下对磁流变抛光区域压力的研究,当抛光区域中磁流变抛光液进入凸光学元件前段时,磁流变抛光区域中凸光学元件的嵌入角度不断增大,其压力不断增加；当磁流变抛光区域中磁流变抛光液进入凸光学元件后半段时,磁流变抛光区域中凸光学元件的嵌入角度不断加大,其压力不断减小；当磁流变抛光液与凸光学元件出口的位置时,压力变化为零。