一种基于PEM和EOM联合调制的波片参量检测方法

李春阳,张敏娟,李克武,杨 坤,辜 航,张 宁

(1.中北大学信息与通信工程学院,山西 太原 030051;2.中北大学山西省光电信息与仪器工程技术研究中心,山西 太原 030051)

1 引 言

在偏振光学中,波片通常由双折射晶体制成,是物理学、光偏振领域、光学精密测量等领域中应用广泛的重要光学元件。但由于制造工艺等因素,实际相位延迟量测量往往有一定的偏差[1]。光的相位和偏振状态的变化取决于波片的关键参数相位延迟量和快轴方位角。当波片稍有变化时,光经过波片后相位和偏振态将发生明显的变化。因此在使用波片之前需要对波片参量精确测量,研究波片相位延迟量和快轴方位角的一种新测量方法具有重要意义[2]。

目前,对光学材料波片双折射参量的检测方法主要包括旋转消光法、移相法、傅里叶波片法、电光调制法、偏振光迈克尔逊干涉法、椭偏测量法[3-7]等,这些测量方法都 有各自的适用范围和优缺点。旋转消光法是通过光强的变化测量波片的相位延迟量,测量过程容易引起误差；移相法、傅里叶波片法都需用到一个高精度的标准波片进行相位补偿,无法准确测量快轴方位角；迈克尔逊干涉法需要对光程差调零和调节平面反射镜的位置,操作比较复杂,可以同时测量波片的相位延迟量和快轴方位角,但是该方法测量结果易受环境干扰,稳定性较低。椭偏测量法则是需要使用椭偏仪、单色仪等多个光学器件,只能测量波片一定波长范围内的相位延迟量,方法有局限性同时比较容易引入测量误差。

电光调制法可以测量任意相位延迟量的波片,但因为分束器的自然双折射等因素使光束不稳定导致其精度不高。因此与传统的检测方法相比本文利用弹光调制(PEM)具有光谱范围宽、调制频率高等优势[8]和电光调制器(EOM)具有相位延迟量可控、响应速度快的优点,提出一种基于弹光和电光联合调制的波片双折射参量检测方法,基于FPGA与数字锁相技术提取调制信号的倍频分量和直流分量,根据四倍频与二倍频的比值保持PEM的稳定控制,并在片上可编程系统中对EOM的两种工作模式进行数据分析与算法优化处理,可以快速精确测量并显示波片相位延迟量和快轴方位角的大小,大大提高了测量的速度与准确度。

2 基于PEM和EOM联合调制的检测系统

检测系统的光路如图1所示,激光器发出激光依次通过起偏器P1、PEM、分束器、待测波片、EOM、检偏器P2,将入射激光分出两路信号,探测器1获取的是激光经PEM、待测波片、EOM后的调制信号,探测器2获取的是激光只经过PEM后的调制信号,监测PEM的稳定性。

图1 系统光路框图

为了方便运用Stokes参量和穆勒矩阵,PEM调制快轴保持水平方向(x轴),起偏器、检偏器保持快轴方向成45°和-45°,而EOM调制快轴成-22.5°。检测系统中所有的光学元件都可以用穆勒矩阵进行表示,斯托克斯参量则可以用来描述偏振光和全偏振光[9]。通过起偏器后的入射光(Stokes)参量为:

Sin=I0[1,0,1,0]T

(1)

式中,I0表示通过起偏器后光束的总强度。PEM与检偏器P2的穆勒矩阵可表示为:

(2)

式中,δ0与f分别为弹光调制器的调制幅值和调制频率。

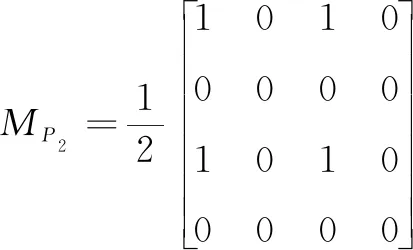
(3)

样品的相位延迟和快轴方位角分别用β和θ来表示,则待测样品的穆勒矩阵为:

(4)

EOM驱动控制器能输出0～15 kV的可调电压,未施加电场V=0时,电光调制器无双折射现象发生,即入射光通过EOM不发生调制；当施加半波电压V=Vπ时,使用半波电压1132 V,此时调制快轴平行于晶片Y方向,入射光经电光调制器发生双折射产生的o光和e光的两个偏振分量为π[10]。因此EOM在未施加电场V=0和施加半波电压V=Vπ两种情况下的穆勒矩阵要分别描述:

(5)

入射光在各光学元件忽略光在传输过程中的损失,处于轴向理想匹配状态下,经检偏器后出射光的Stokes参量可以表示为:

Sout=SinMPEMMSMEOMMP2

(6)

将式(1)～(5)代入式(6),在EOM未施加电场时探测器输入的光强为I1,施加半波电压后输入的光强为为I2:

(7)

利用第一类贝塞尔级数简化展开:

(8)

公式中,k表示正整数,J0、J2k、J2k-1分别表示为第0阶、2k阶、(2k-1)阶贝塞尔级数。将式(8)代入式(7),忽略3阶及3阶以上的贝塞尔级数,检测得出电光调制器在两种状态下的光强分别为:

(9)

由上式可知,待测波片的双折射参量均包含在调制信号的基频分量中。将PEM的相位调制幅值设置为δ0=2.405 rad,使得J0(2.405)=0,同时也要控制EOM的工作模式,在两种情况下输出的直流信号为:

(10)

式中,K1是由光电探测器转换系数决定。根据数字锁相技术在EOM的两种工作模式下分别提取弹光调制基频项:

(11)

式中,K2是与前置放大和锁相放大增益有关的常数。 消去初始光强I0和光电探测器转换系数K1,可以消除入射激光不稳定对系统测量准确度的影响,将数字锁相输出的基频分量与直流分量进行对比可得到:

(12)

利用PEM和EOM联合调制偏振光,在EOM不施加电压和施加半波电压时分别检测偏振信号的基频分量和直流分量,求解出相位延迟量和快轴方位角:

(13)

3 PEM稳定控制与数字锁相技术

由于弹光调制器为谐振器件,存在频率温漂特性以及驱动的不稳定都可导致其相位调制幅度发生变换引入测量误差[11],对数字锁相的效果有一定的影响,因此在本系统中需要稳定PEM实现偏振信号的检测。

检偏器P3的Muller矩阵为:

(14)

入射光经过图1所示参考光路后,由式(1)、式(2)和式(14)得偏振信号,得出射偏振光的Stokes参量:

Sout=SinMPEMMP3

(15)

探测器2接收到的光强用第一类贝塞尔级数展开为:

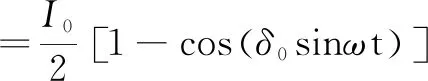
(16)

则探测器的输出为:

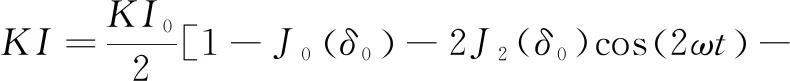
2J4(δ0)cos(4ωt)-2J6(δ0)cos(6ωt)-…]

(17)

式中,K是与光电探测器转换系数有关的光电常数。二倍频分量、四倍频分量分别为:

(18)

(19)

因此由贝塞尔函数的有关公式(19)可知两者的比值为:

(20)

倍频信号由探测器2输出,因此可以通过数字锁相技术得到,为了减小误差准确求解相位延迟量β和快轴方位角θ,由0阶贝塞尔级数可以求出使J0(δ0)=0时对应的点,即PEM的相位调制幅值需要设置为δ0=2.405 rad,此时的倍频比值J4/J2=0.15。弹光调制器相位延迟量与倍频的比值、0阶贝塞尔级数关系如图2所示。

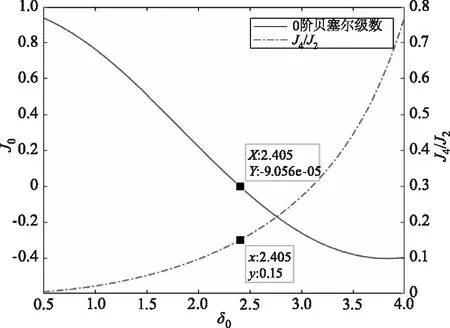
图2 相位延迟量与倍频比值、0阶贝塞尔级数的关系

在同一FPGA内使用数字锁相技术,利用DDS技术生成控制弹光调制器工作的方波信号和数字锁相器的正余弦参考信号,保持相位控制字不变,改变频率控制字和占空比控制字生成需要的方波信号,以此控制驱动弹光调制器的频率和幅值,使驱动信号的频率与弹光调制器的谐振频率相同,在同一时钟下,数字锁相得到的结果具有更好的准确性与稳定性。数据处理如图3所示,探测器输出的信号经过A/D转换与参考信号进行乘累加运算,可以准确的提取其一、二、四倍频分量,通过四倍频与二倍频的比值变化调节弹光调制器驱动信号的幅值,维持δ0=2.405 rad,使弹光调制器稳定工作。

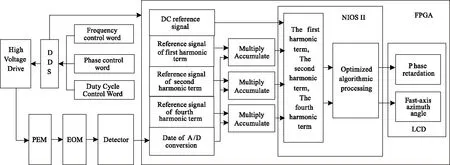
图3 数据处理流程图

由波片相位延迟量和快轴方位角测量原理和数字锁相原理可知,计算过程中含有大量的平方运算和开方运算,用硬件逻辑电路实现对数据的处理将会消耗大量资源,考虑硬件资源与设计需要,实验中搭建片上可编程系统,运用数字锁相将参考信号和A/D模数换信号进行乘累加运算,得到的数据输入到 NIOS II处理器进行优化运算,并将计算结果输出到 FPGA,实时显示相位延迟量和快轴方位角的测量结果。

4 实验验证与数据分析

实验系统如图4所示包括光学系统、高压驱动电路、FPGA 数字锁相电路、电源电路、LCD显示五部分,入射光的光源采用波长为632.8 nm的He-Ne激光器；起偏器和检偏器选用Thorlabs公司消光比为105∶1的格兰泰勒偏振棱镜；弹光调制器为实验室自行研制的具有双压电石英驱动的八角形结构硒化锌晶体,使用谐振频率为50.284 kHz；分束器采用的是大恒光电公司生产的的5∶5的分光镜；电光调制器是加工制作的有横向体电光效应的铌酸锂单轴晶体,光束通过时沿晶片光轴Z方向、Y方向上分别通光与施加电场；待测波片采用Thorlabs公司WPH05M-633 nm的零级1/4标准波片,因此波片相位延迟量理论值为π/2 rad。探测器1和探测器2采用的均是Thorlabs公司生产的FDS010硅光电二极管,可对波长范围为200～1100 nm的偏振光进行测量,满足系统光束要求。

图4 测量系统实物图

弹光调制器容易受温漂影响,在波片测量前弹光调制幅值维持在δ0=2.405 rad,保持测量系统中PEM的稳定性。改变频率控制字和占空比控制字,使驱动信号的频率与弹光调制器的谐振频率相同,调节弹光调制器高压驱动信号的幅值,使四倍频项与二倍频项比值J4(2.405)/J2(2.405)=0.15,如图5所示中曲线表示5 min内两个倍频项比值随时间的变化曲线,证明了此时PEM处于稳定状态,消除了因温漂带来的误差。

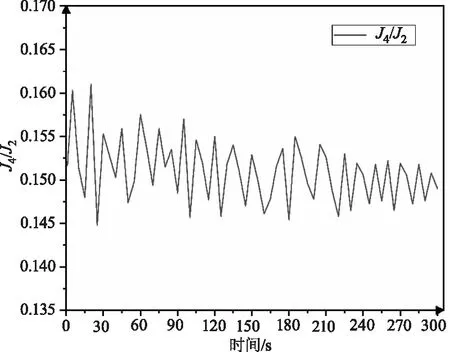
图5 倍频项比值随时间变化

实验中保持室内温度25°,波动范围达到0.1 ℃,使测量环境的温度几乎不会引起误差影响实验结果。光束首先通过未施加电场的电光调制器,经光电探测器把光信号转化为电信号输入FPGA中完成数据处理,实现倍频信号的提取,基于FPGA内部方便快捷的软核,在片上可编程系统中优化测量算法完成数据处理得到未施加电场时的一倍频分量与直流分量,延时30 s同时对电光调制器施加半波电压,此时FPGA再次对探测信号进行数字锁相,在软核中数据处理得到波片施加电场时的一倍频分量,然后对存储在FPGA中的同一快轴方向角上两次不同的一倍频分量进行算法处理,得出结果通过LCD实时显示。旋转波片从0°开始每隔10°测量一次,重复以上测量过程,最终旋转至170°,每次可以显示不同快轴方向角上的相位延迟量与快轴方向角,测量结果与对应的相对误差如图6所示。

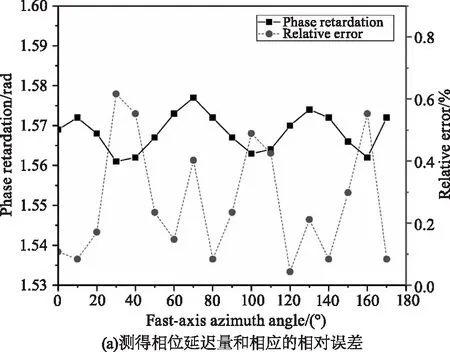
图6 相位延迟量与快轴方向角的测量结果

由测量结果可得,待测1/4波片经过多次测量后相位延迟量的平均测量值为1.568 rad,标准偏差为0.45 %,当波片快轴方位角位于30°时,由相对偏差公式λ=Δ/L×100%,(Δ为绝对偏差,L为理论值)可得,此时有最大相对偏差为0.61 %；当波片快轴转到120°时,存在最小相对偏差为0.04 %,由平均相对偏差公式α=λ/μ×100%,(λ为相对偏差,μ为测量次数)可知,相位延迟量测量的平均相对偏差为0.27 %,而快轴方位角测量值的平均相对偏差为0.25 %,波片快轴转到120°时有最大相对偏差为0.43 %。测量结果表明该方法具有较高的测量精度。

对测量系统的稳定性,每30 s测量一次1/4波片并记录实验结果,测量时间共300 s,将快轴方位角分别设置60°和90°时,实验结果如图7 所示,相位延迟量平均测量值分别为1.572 rad和1.569 rad,平均相对偏差分别为0.12 %和0.11 %,快轴方位角平均测量值分别为60.10°和90.07°,平均相对偏差分别为0.20 %和0.21 %,证明该测量系统具有很强的稳定性。

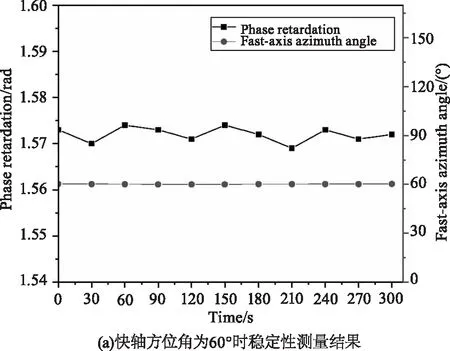
图7 不同快轴方向角测量系统稳定性

实验结果表明,该测量系统测量精度高、重复性较好,测量方法简单可以快速准确检测波片的优良。

实验中的主要误差为器件光轴定位精度、操作过程中旋转角度误差等。检偏器位置判断精度引起的误差,可以通过检测信号的基频成分实现高精度的检偏器位置判断；被测波片的快轴方向与x轴的夹角偏离导致的误差,当被测波片的快轴方向与x轴的夹角偏离45°时,其矩阵变化将导致测量结果产生误差,这项误差主要受光学分度头的调整精度决定；待测波片表面与光路不严格垂直导致的测量误差,通过调整反射光点位置可以保证被测波片表面与光束方向的垂直度从而使误差减小。

5 结 论

本文基于弹光和电光联合调制的方式对波片的相位延迟量和快轴方位角进行了快速准确测量。通过切换EOM的工作模式,基于斯托克斯参量和穆勒矩阵建立波片参量检测模型,并将PEM相位延迟量稳定控制在2.405 rad以简化测量算法,将数字锁相技术应用到波片参量测量中,实现基频、倍频分量的提取,优化算法快速准确地检测波片的相位延迟量和快轴方位角。实验测量结果相位延迟量和快轴方位角的平均相对偏差分别为0.27 %和0.25 %。本方法在保证测量精度的前提下,提高了测量速度,能够同时测量任意波片的相位延迟量和快轴方位角。