基于虚拟同步机控制的新能源发电并网系统小干扰稳定临界短路比
2022-03-18康思伟董文凯郭诗然孙红军谢小荣
康思伟,董文凯,郭诗然,孙红军,谢小荣
(1.中海油融风能源有限公司,上海市 200335;2.电力系统及发电设备控制与仿真国家重点实验室(清华大学电机系),北京市 100084)
0 引 言
目前,基于矢量控制的电压源型换流器(voltage source converter,VSC)在新能源发电领域具有广泛应用,其在为新能源发电提供快速灵活并网控制的同时,也造成电力系统中旋转惯量的降低,且难以在弱电网条件下保持良好的稳定性。为应对传统VSC不具备旋转惯量、无法有效为交流系统提供频率和电压支撑的问题[1-3],2007年,德国劳斯克塔尔工业大学Beck教授率先提出虚拟同步机(virtual synchronous generator,VSG)的概念,即将同步发电机动态方程引入换流器控制[1-6],使其可以模拟同步机的惯性和阻尼等输出特性,具备为交流系统提供频率和电压支撑的能力。这一提法随后在全球范围内得到广泛关注与认可。
除为交流系统提供频率和电压支撑外,近年来的研究表明,电压控制型VSG可在弱电网甚至是极弱电网的条件下,保持良好的小干扰稳定特性[4-13]。文献[4-5]针对基于VSG的双馈风机并网系统,通过模式分析发现,在弱电网甚至是极弱电网的条件下,VSG的振荡模式仍具有较好的阻尼特性,系统具备在小干扰作用下保持良好运行稳定性的能力。文献[6-13]基于阻抗模型,分析了VSG换流器并网系统在弱电网与极弱电网条件下的小干扰稳定性,发现在短路比(short circuit ratio,SCR)不断减小,甚至是接近于1的情况下,阻抗矩阵特征值的奈奎斯特曲线仍与(-1,0)之间保持一定距离,即系统仍具有一定的稳定裕度[6-13]。考虑到对于传统VSC并网系统,大量理论研究与工程实践都表明,系统在弱电网或极弱电网的条件下容易出现小干扰稳定性问题[14-18],因此,VSG可能成为应对弱电网条件下电能变换需求的有效解决方案。
但是,文献[19-20]进一步指出VSG更适合在弱电网条件下运行,反而不适合强电网。文献[21-22]基于线性化状态空间模型,分析了VSG换流器并网系统小干扰稳定性,发现随交流电网强度提高,VSG振荡模式在复平面上向右移动,造成系统小干扰稳定性降低。文献[23]基于阻抗模型,分析了VSG经串补线路并网系统的小干扰稳定性,发现随串补度提高,系统稳定性降低。在此,需要补充说明的是,当前VSG可分为电压控制型和电流控制型两类,对弱电网条件的良好适应性是针对电压控制型VSG而言[8],文献[21-23]中的结论也是基于仅具有电压控制环的VSG并网系统获得的。在以上研究的基础上,为有效保障系统稳定性、充分发挥此类VSG对弱电网的良好适应性与为交流系统提供频率和电压支撑的能力,本文进一步探讨与明确考虑不同电网强度影响的VSG并网系统小干扰稳定性判定方法以及系统临界稳定条件,为未来VSG并网系统规划提供参考和借鉴。
为此,本文首先建立VSG并网系统小信号模型,并将其整理为两输入两输出单位负反馈系统的表示形式。然后,基于广义奈奎斯特判据,提出一种考虑不同电网强度的VSG并网系统小干扰稳定性判定方法,定义系统小干扰稳定临界短路比(critical short circuit ratio,CSCR)。最后通过仿真算例,验证所提方法的有效性。
1 虚拟同步机并网系统小信号模型
VSG并网系统示意如图1所示。其中,VSG的动态可描述为[8]:
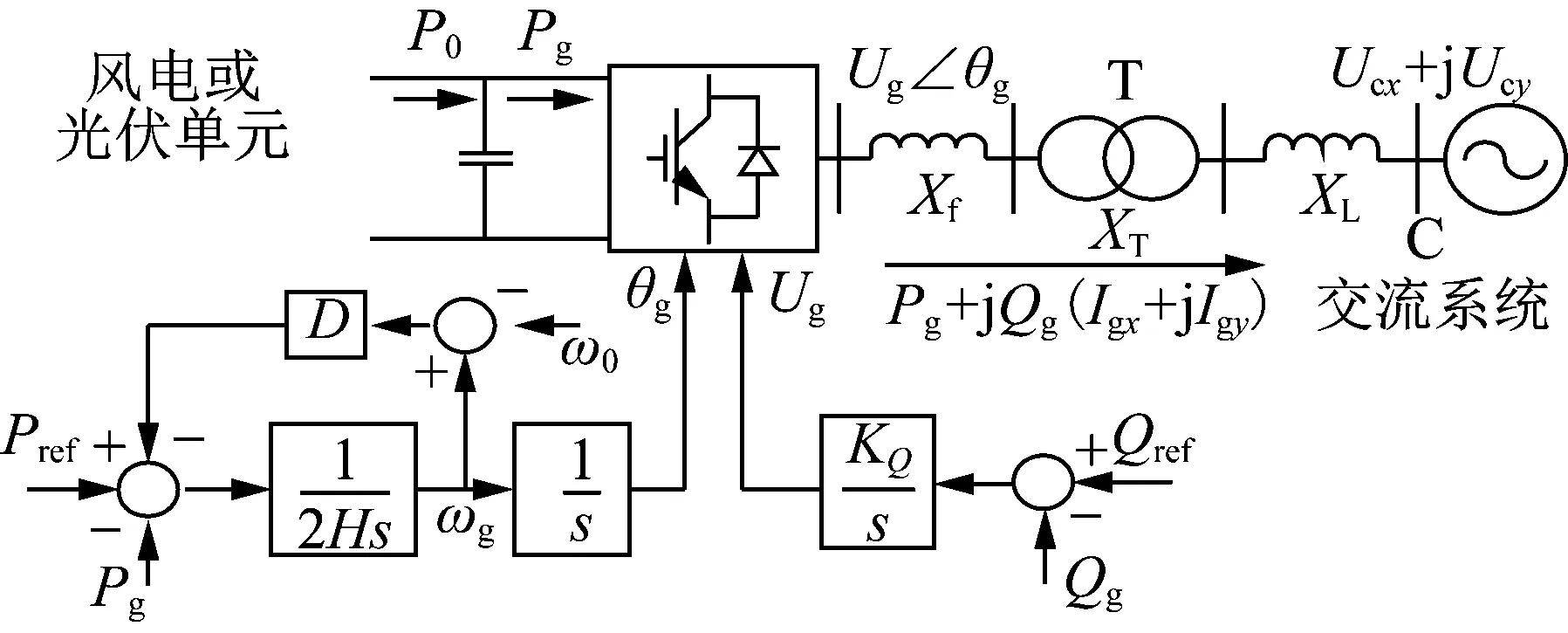
图1 VSG并网系统示意图Fig.1 A grid-connected VSG system
(1)
(2)
式中:ωg为VSG虚拟角频率;ω0为系统额定角频率;Ug、θg分别为VSG输出电压幅值和相角;H、D、KQ分别为VSG惯性常数、阻尼系数和无功控制器增益系数;Pref、Qref分别为VSG输出有功和无功的参考值;Pg、Qg为VSG输出有功和无功功率;Ugx、Ugy为交流电网公共x-y坐标系下VSG端x轴和y轴电压。
Pg+jQg=(Ugx+jUgy)(Igx-jIgy)
(3)
式中:Igx、Igy表示交流电网公共x-y坐标系下VSG端x轴和y轴的输出电流。
将式(1)—(3)线性化并写为状态空间的表示形式:
(4)
式中:ΔXg=[ΔωgΔθgΔUg]T;ΔIg=[ΔIgxΔIgy]T;ΔUg=[ΔUgxΔUgy]T;Ag=

图1中:Xf为滤波器电抗;XT为升压变压器电抗;XL为连接线路电抗。令XE=Xf+XT+XL表示VSG与交流系统间连接系统总电抗,则有
(5)
式中:Ucx、Ucy表示交流电网公共x-y坐标系下,图1中母线C的电压。
将式(5)线性化并写为状态空间的表示形式:
(6)

由式(4)和式(6),可得图1所示VSG并网系统的线性化状态空间模型:
(7)

由式(4)可得VSG小信号传递函数模型为:
ΔUg=G(s)ΔIg
(8)
式中:G(s)=Cg(sI3-Ag)-1Bg,I3为3×3单位矩阵。
将式(6)写为传递函数的形式:
(9)
式中:H(s)=(sI2-AL)-1BL,I2为2×2单位矩阵。
由式(8)和式(9)可知,图1所示的VSG并网系统小信号模型可表示为图2所示的形式;VSG并网系统的小信号传递函数模型如式(10)所示。
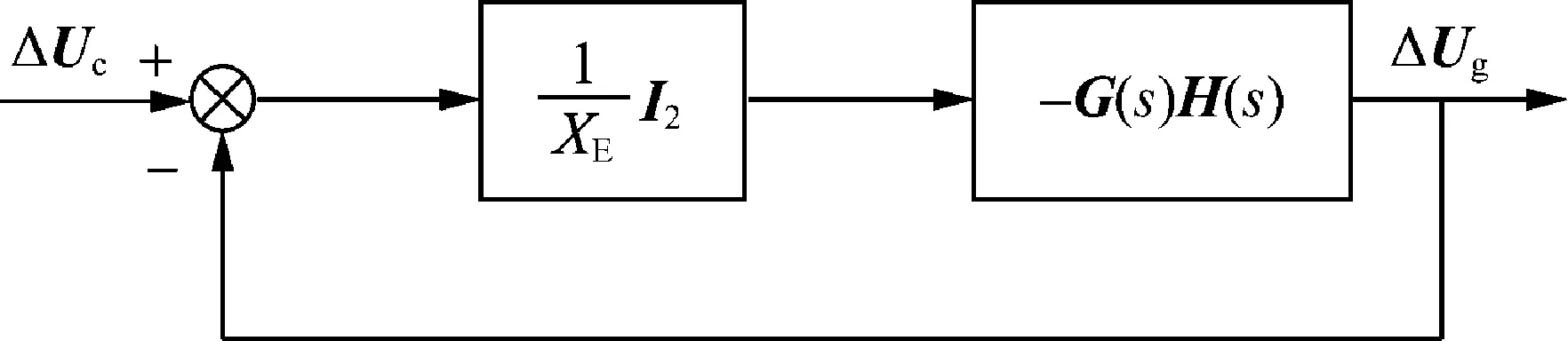
图2 VSG并网系统小信号模型Fig.2 Small-signal model of a grid-connected VSG system
ΔUg=N(s)ΔUc
(10)
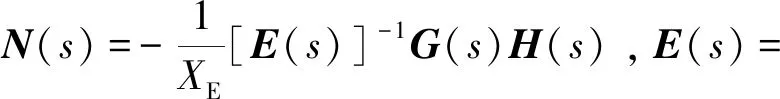
2 基于广义奈奎斯特判据的虚拟同步机并网系统小干扰稳定临界短路比
第1节给出了VSG并网系统小信号模型,本节将在此基础上探讨考虑不同电网强度影响的系统小干扰稳定性判定方法与临界稳定条件。
2.1 虚拟同步机并网系统短路比的定义
交流电网强度通常采用VSG并网点的短路比衡量,具体到图1所示系统,根据文献[24],其短路比σSCR可表示为:
(11)
式中:S表示VSG额定容量标幺值。SCR越小,交流电网强度越弱,SCR的取值为2~3时,为弱电网;SCR小于2时,为极弱电网[16-17]。在此需要作进一步说明的是,对于仅具有电压控制环的VSG而言,可将VSG端口滤波电抗看作连接系统的一部分,并将其计入系统SCR中[24];而对于具有矢量电流控制环节的并网换流器而言,滤波电抗应作为换流器的一部分而不能考虑到短路比当中。
2.2 不同电网强度下VSG并网系统小干扰稳定性判定方法
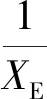
将回率矩阵F(s)的特征值记为R1(s)和R2(s),根据广义奈奎斯特判据,若系统开环稳定,则可由R1(s)和R2(s)的奈奎斯特曲线是否逆时针包围(-1,0)判断图2所示系统的稳定性[25],具体说明如图3所示。
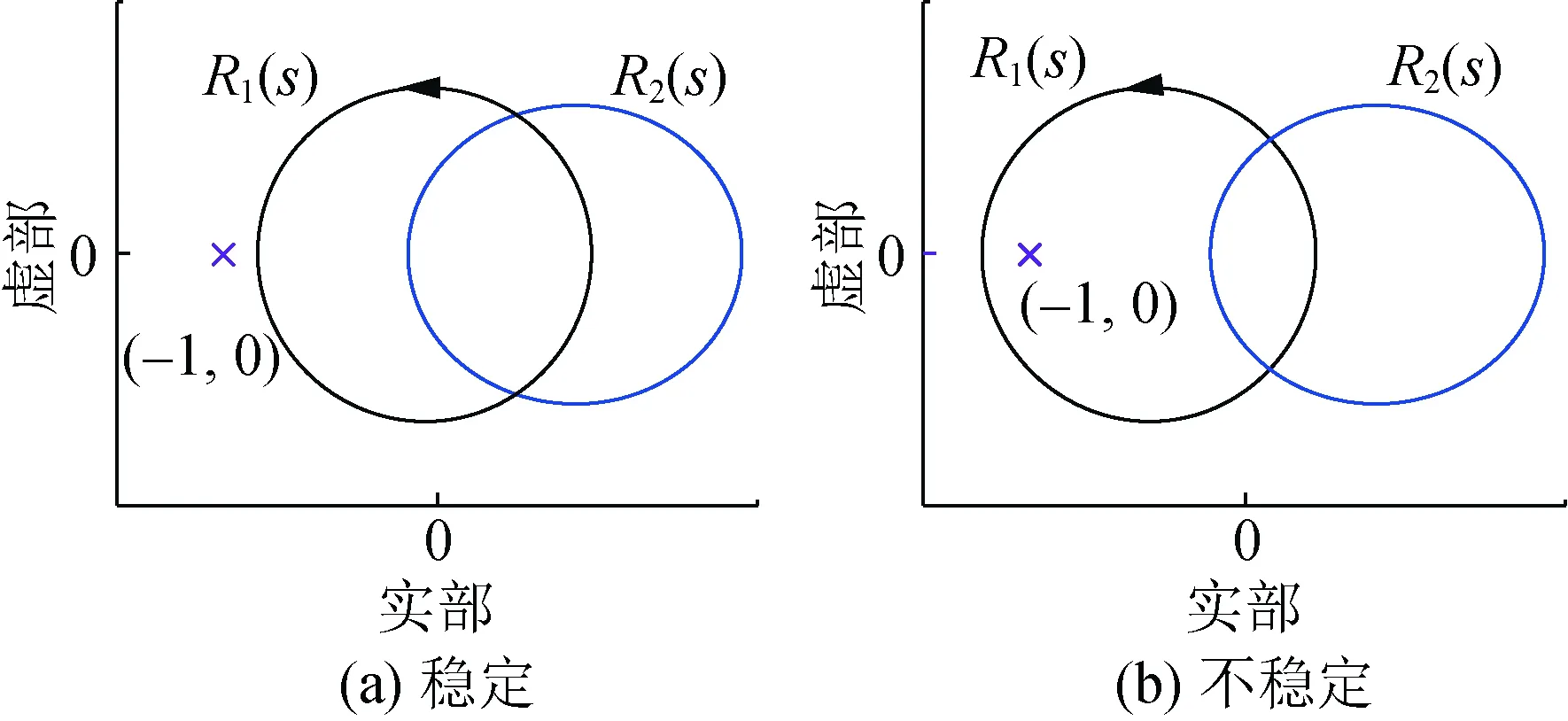
图3 回率矩阵特征值的奈奎斯特曲线Fig.3 Nyquist plots of eigenvalues of return ratio matrix
若矩阵-G(s)H(s)的特征值为λ1(s)和λ2(s),则有λ1(s)=XER1(s)和λ2(s)=XER2(s)。因此,也可根据λ1(s)和λ2(s)的奈奎斯特曲线是否逆时针包围(-XE,0)来判断图2所示系统的稳定性,具体说明如图4所示。
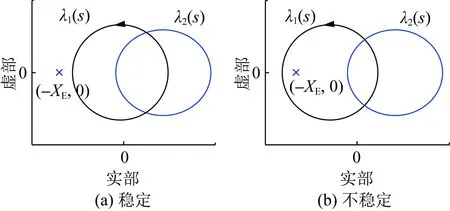
图4 矩阵-G(s)H(s)特征值的奈奎斯特曲线1Fig.4 Nyquist plot 1 of eigenvalues of -G(s)H(s)
为便于说明问题,图4给出的奈奎斯特曲线的形式较为简单,实际上,还可能出现λ1(s)和λ2(s)的奈奎斯特曲线顺时针包围(-XE,0)的情况,此时应考虑与顺时针包围的曲线抵消后,(-XE,0)是否会被λ1(s)和λ2(s)的奈奎斯特曲线“净”逆时针包围[25],来判断系统稳定性。具体说明如图5所示,图5(a)中,(-XE,0)被顺时针和逆时针包围的圈数均为1,净逆时针包围圈数为0,系统稳定;图5(b)中,净逆时针包围圈数为1,系统失稳。
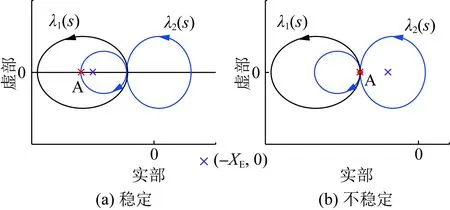
图5 矩阵-G(s)H(s)特征值的奈奎斯特曲线2Fig.5 Nyquist plot 2 of eigenvalues of -G(s)H(s)
若定义奈奎斯特曲线由上向下穿过实轴为“正穿越”,且与实轴的交点为“正穿越点”,由下向上穿过实轴为负穿越,与实轴的交点为“负穿越点”,显然,正穿越对应逆时针闭合曲线的开始或顺时针闭合曲线的结束,负穿越恰好与之相反。若某一穿越点及其左侧所有穿越点中,正穿越点数多于负穿越点数,则该穿越点可称为“净正穿越点”。由此:
1)若实轴上(-XE,0)左侧存在穿越点,且左侧距(-XE,0)最近的穿越点为净正穿越点,则(-XE,0)被奈奎斯特曲线逆时针包围,系统失稳;
2)若有穿越点与(-XE,0)重合,则系统临界稳定;
3)若上述情况1)和2)均未出现,则系统稳定。
以图5为例,图5(a)中A点及其左侧有一个负穿越点和一个正穿越点,A点非净正穿越点,系统稳定;图5(b)中,A点及其左侧有3个正穿越点和2个负穿越点,A点为净正穿越点,系统失稳(蓝色曲线在A点处有2次正穿越、黑色曲线有1次负穿越,此处应记为2个正穿越点和1个负穿越点)。
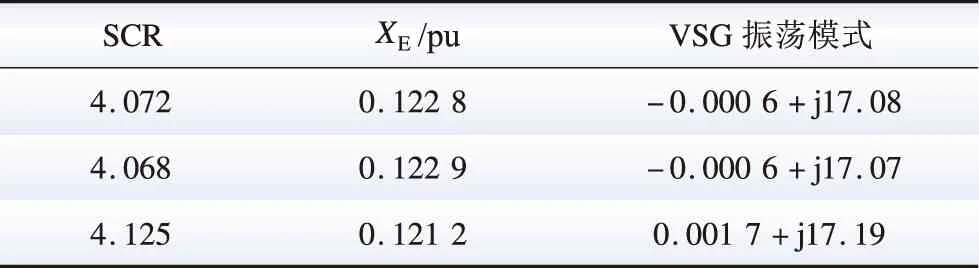
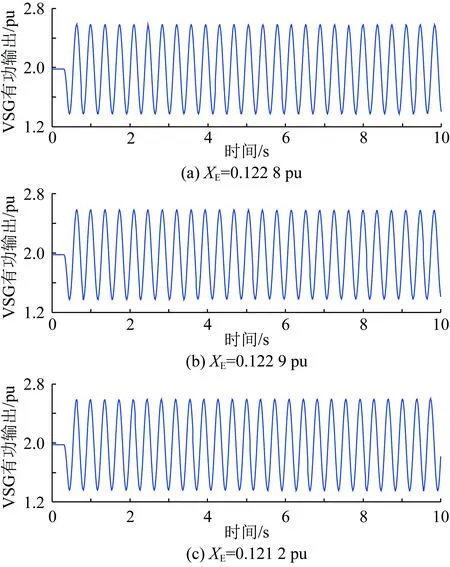
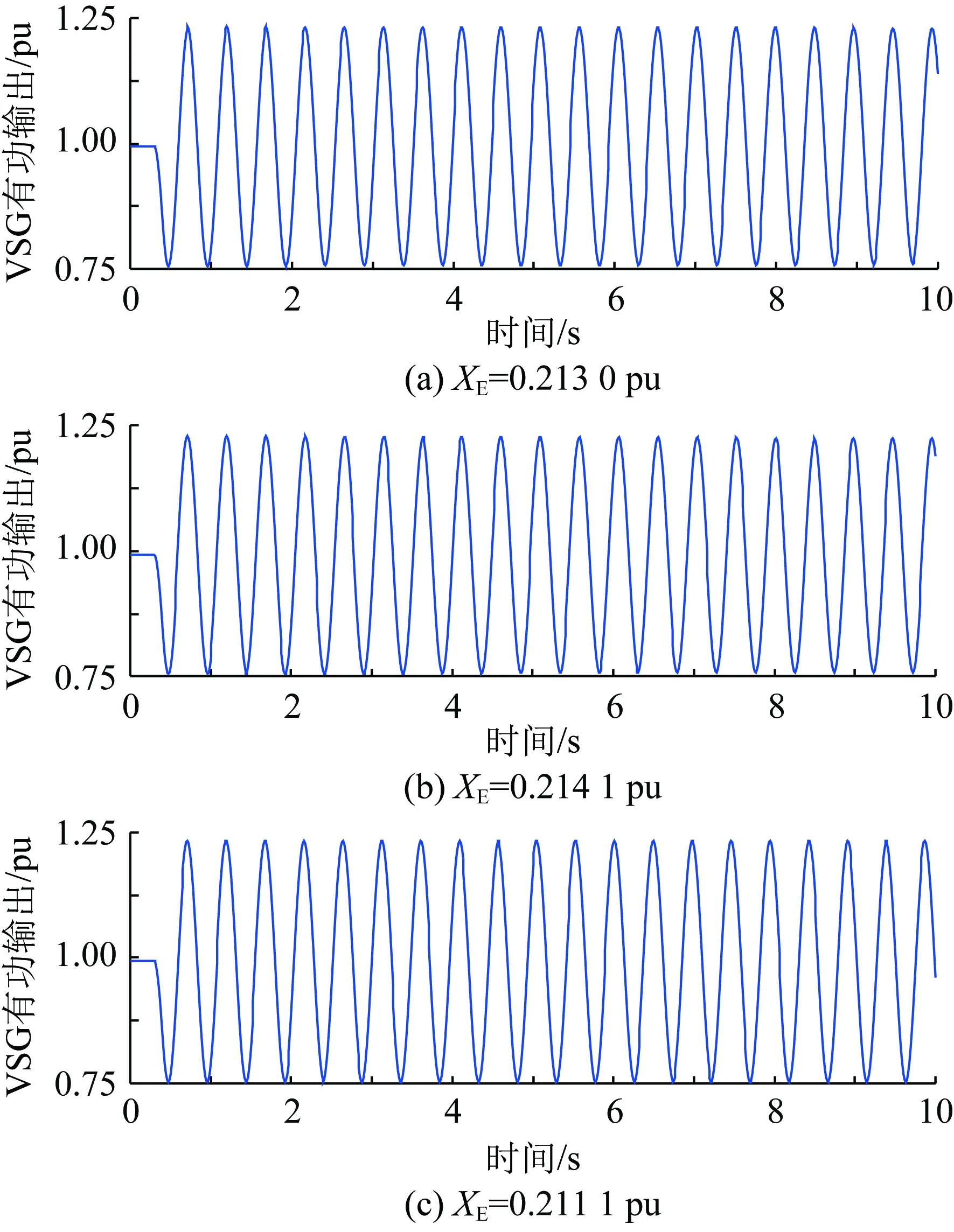
由式(4)、式(6)、式(8)和式(9),对于一给定的VSG,G(s)和H(s)的表达式与XE无关,即λ1(s)和λ2(s)奈奎斯特曲线的绘制结果基本不受XE变化的影响。在XE变化的过程中,(-XE,0)沿实轴移动,其左侧实轴被λ1(s)和λ2(s)奈奎斯特曲线穿越的情况可能也会相对发生变化,从而造成系统稳定性的变化。结合此前的分析,沿实轴由左向右,一个净正穿越点Ai(ai,0)和此后与其相邻的非净正穿越点Bi(bi,0)之间构成一个失稳区间φi={(x,0)|ai 图6 XE减小造成VSG并网系统稳定性变化图示说明Fig.6 Illustration on the stability variation of the grid-connected VSG system due to the decrease of XE 综上,可获得一种判定给定VSG在不同电网强度下构成并网系统小干扰稳定性的方法如下: 1)根据式(4)、式(5)、式(8)和式(9),建立传递函数矩阵G(s)和H(s),并绘制矩阵-G(s)H(s)特征值的奈奎斯特曲线; 2)根据奈奎斯特曲线对实轴负半轴的穿越情况,确定ξ上的失稳区间φ1i(i=1,2,…,m1,m1为区间ξ内失稳区间的个数); 3)当(-XE,0)∈φ1i时,系统失稳;当(-XE,0)与区间ξ内的穿越点重合时,系统临界稳定。 采用以上方法,对于一个VSG,在给定运行状态下,仅需一次绘制系统的奈奎斯特曲线,便可获得使VSG并网系统小干扰失稳的XE的取值区间。在未来,VSG生产厂家可考虑选择几种典型运行状态,给出图6所示的VSG并网系统奈奎斯特曲线及失稳区间,这一信息对于VSG并网系统设备选择和规划具有很好的借鉴和指导意义。 考虑到现有研究表明,对于图1所示的电压控制型VSG,其更适合于弱电网条件,反而不适合强电网[19-22]。文献[21]和[22]中进一步表明,随XE减小,VSG振荡模式在复平面上向右移动,系统小干扰稳定性降低。XE=0 pu时VSG并网系统小干扰稳定性推导见附录A,根据附录A中的推导,当XE=0 pu时,系统小干扰失稳,即VSG直接接入无穷大电网时失稳,对此,文献[8]和[23]基于阻抗模型,得到相同的结论。因此,通常来讲,应存在一个临界电网强度或临界SCR,在系统实际SCR超过该临界SCR时,系统小干扰失稳。 与上述分析对应,在区间ξ内存在一个净正穿越点A(a,0),A点与原点之间构成一个失稳区间,在XE减小的过程中,(-XE,0)沿实轴向原点移动,不断靠近A点,系统小干扰稳定裕度降低,(-XE,0)与A点重合时,系统临界稳定,(-XE,0)移动至A点右侧时,系统小干扰失稳。据此,可获得VSG并网系统小干扰稳定临界短路比的定义与确定方法如下: 令VSG处于额定运行状态,根据式(4)、式(5)、式(8)和式(9),建立矩阵-G(s)H(s),并绘制其特征值的奈奎斯特曲线,得到区间ξ内的净正穿越点A(a,0);对应的VSG并网系统小干扰稳定临界短路比(critical short circuit ration considering small-signal stability,CSCR_S)σCSCR_S为: (12) 在VSG处于额定运行状态时,为确保VSG并网系统的小干扰稳定性,系统实际SCR应小于式(12)给出的CSCR_S,对此应在VSG并网系统规划阶段重点考虑。 从本节的分析可以看出,随着电网强度的提升(或SCR的增大),VSG并网系统小干扰稳定性降低,当实际SCR大小超过所得CSCR_S时,系统失稳。对于VSG控制的原理和模型,本文主要以图1和式(1)、(2)所示的核心部分为例进行介绍;理论上讲,VSG中应引入类似于传统同步机中的调差环节,但是此时VSG的小信号模型仍能表示为式(4)所示形式,因此,本节所提CSCR_S的求解方法,在考虑VSG控制中的调差等更为细节的环节时依然适用。此外,VSG参数不同,其并网系统的CSCR_S的大小也不相同。由于VSG并网系统数学模型的复杂性,对于控制参数和调差环节对系统小干扰稳定性的影响,当前尚无法通过类似于图2所示形式直观地反映出来,须对具体案例进行具体分析。本文主要针对给定VSG的小干扰稳定临界短路比的求解,对于控制参数、运行点和调差环节等部分对系统CSCR_S的影响机理和规律,则还须进一步研究,本文不做讨论。 本节采用图1所示系统,验证第2节所提小干扰稳定性判定方法和CSCR_S的有效性,VSG参数为:D=0.6、H=5、KQ=0.4,仿真软件采用Matlab。 本节分别在VSG稳态功率输出S0为2.0 pu和1.0 pu(功率因数均为0.98)的情况下,分析XE变化时VSG并网系统的小干扰稳定性,验证2.2节所提小干扰稳定性判定方法的有效性。 对于S0=2.0 pu的情况,(-XE,0)可能的运动区间为ξ={(x,0)|-0.5 图7 S0=2.0 pu时的奈奎斯特曲线(算例1)Fig.7 Nyquist plots when S0=2.0 pu (case 1) 然后,在XE由0.30 pu减小至0.05 pu的过程中,建立式(7)所示VSG并网系统线性化状态空间模型,并计算矩阵A的特征值,得到VSG振荡模式如表1所示。由表1可以看出,随着XE的减小,振荡模式阻尼减小。当XE<0.122 8 pu时,系统小干扰失稳。 表1 S0=2.0 pu时VSG振荡模式计算结果(算例1)Table 1 Computational results of oscillation modes of the VSG when S0=2.0 pu (case 1) 最后,对算例系统小干扰稳定性进行非线性仿真分析。仿真中的扰动设置为:0.2 s时,输入VSG的有功功率P0降低20%,并于0.1 s内恢复。仿真结果如图8所示,可以看出,XE=0.20 pu时,系统稳定,XE=0.10 pu时,系统失稳,与此前基于线性化模型所得结论一致。 图8 S0=2.0 pu时非线性仿真结果(算例1)Fig.8 Non-linear simulation results when S0=2.0 pu (case 1) 对于S0=1.0 pu的情况,(-XE,0)的运动区间为ξ={(x,0)|-1 图9 S0=1.0 pu时的奈奎斯特曲线(算例1)Fig.9 Nyquist plots when S0=1.0 pu (case 1) 然后,在XE由0.65 pu减小至0.10 pu的过程中,建立式(7)所示VSG并网系统线性化模型,并计算矩阵A的特征值,得到VSG振荡模式如表2所示。由表2可以看出,随着XE的减小,振荡模式阻尼降低。当XE<0.213 pu时,系统小干扰失稳。 表2 S0=1.0 pu时VSG振荡模式计算结果(算例1)Table 2 Computational results of oscillation modes of the VSG when S0=1.0 pu (case 1) 最后,对系统小干扰稳定性进行非线性仿真分析。仿真中扰动设置同S0=2.0 pu的情况,仿真结果如图10所示,可以看出,XE=0.30 pu时,系统稳定,XE=0.10 pu时,系统失稳,与此前所得结论一致。 图10 S0=1.0 pu时非线性仿真结果(算例1)Fig.10 Non-linear simulation results when S0=1.0 pu (case 1) 本节分别以VSG额定容量为2.0 pu和1.0 pu两种情况为例,验证2.3节给出的VSG并网系统小干扰稳定临界短路比的有效性。 对于VSG额定容量为2.0 pu的情况,设定S0=2.0 pu,功率因数为0.98。由3.1节中图7,系统小干扰稳定临界短路比为4.072。为进一步验证2.3节定义的小干扰稳定临界短路比的有效性,分别在XE为0.15和0.25 pu的情况下,建立VSG的小信号模型,并绘制矩阵-G(s)H(s)特征值的奈奎斯特曲线,所得结果如图11所示。可以看出,系统小干扰稳定临界短路比分别为4.068和4.125。 图11 S0=2.0 pu时的奈奎斯特曲线(算例2)Fig.11 Nyquist plots when S0=2.0 pu (case 2) 然后,在系统实际SCR等于以上所得小干扰稳定临界短路比的情况下,建立VSG并网系统线性化模型,计算矩阵A的特征值,得到VSG振荡模式如表3所示,可以看出,当实际SCR等于小干扰稳定临界短路比时,系统基本处于临界稳定状态,验证了小干扰稳定临界短路比的有效性。 表3 S0=2.0 pu时VSG振荡模式计算结果(算例2)Table 3 Computational results of oscillation modes of the VSG when S0=2.0 pu (case 2) 此外,XE取不同值时,以上所得小干扰稳定临界短路比数值也略有差异,这是由于,虽然VSG稳态功率输出恒定,XE取值不同,对图1所示系统作稳态潮流计算,所得VSG端电压和输出电流稳态值不同,造成VSG小信号模型略有差异,矩阵-G(s)H(s)特征值的奈奎斯特曲线也有所不同,由此获得的小干扰稳定临界短路比也略有差异。但是在VSG参数和输出功率恒定的条件下,端电压和输出电流稳态值差异造成的VSG小信号模型的差异不大,因此,XE取不同值时,所得小干扰稳定临界短路比差异不大,且系统实际SCR等于小干扰稳定临界短路比时,VSG并网系统基本在临界稳定状态。 最后,在系统实际SCR等于所得小干扰稳定临界短路比时,进行非线性仿真分析。仿真中扰动设置同3.1节,所得结果如图12所示,可以看出,当实际SCR等于小干扰稳定临界短路比时,系统基本处于小干扰临界稳定状态,验证了小干扰稳定临界短路比的有效性。 图12 S0=2.0 pu时非线性仿真结果(算例2)Fig.12 Non-linear simulation results when S0=2.0 pu (case 2) 对于VSG额定容量为1.0 pu的情况,设定S0=1.0 pu,功率因数为0.98。由图9可得,小干扰稳定临界短路比为4.695。以下进一步给出XE为0.30和0.20 pu时,矩阵-G(s)H(s)特征值的奈奎斯特曲线如图13所示。由图13可得系统小干扰稳定临界短路比分别为4.671和4.737。 图13 S0=1.0 pu时的奈奎斯特曲线(算例2)Fig.13 Nyquist plots when S0=1.0 pu (case 2) 然后,在系统实际SCR等于以上所得小干扰稳定临界短路比的情况下,建立VSG并网系统线性化模型,计算矩阵A的特征值,得到VSG振荡模式如表4所示,可以看出,当实际SCR等于小干扰稳定临界短路比时,系统基本处于临界稳定状态,验证了小干扰稳定临界短路比的有效性。 表4 S0=1.0 pu时VSG振荡模式计算结果(算例2)Table 4 Computational results of oscillation modes of the VSG when S0=1.0 pu (case 2) 最后,在系统实际SCR等于所得小干扰稳定临界短路比时,进行非线性仿真分析。仿真中扰动设置同3.1节,所得结果如图14所示,可以看出,当实际SCR等于小干扰稳定临界短路比时,系统基本处于小干扰临界稳定状态,验证了小干扰稳定临界短路比的有效性。 图14 S0=1.0 pu时非线性仿真结果(算例2)Fig.14 Non-linear simulation results when S0=1.0 pu (case 2) 本文针对仅具有电压控制环的VSG并网系统,基于广义奈奎斯特判据,定义了系统小干扰稳定临界短路比,并得到了一种考虑电网强度影响的系统小干扰稳定性判定方法。 1)建立了VSG并网系统小信号模型,并将其整理为两输入两输出单位负反馈系统的表示形式。 2)采用上述建模表示形式,基于广义奈奎斯判据,获得了一种考虑电网强度影响的系统小干扰稳定性判定方法,定义了系统小干扰稳定临界短路比。 3)通过仿真算例,验证了所提小干扰稳定性判定方法和小干扰稳定临界短路比的有效性。 对于一个具体的VSG,在选定运行状态下,仅需一次绘制奈奎斯特曲线,便可获得使VSG并网系统小干扰失稳连接电抗的取值区间。这一信息对于未来VSG并网规划具有很好的借鉴和指导意义。本文是基于仅具有电压控制环结构的VSG展开研究的,除此之外还有电流控制型等其他结构的VSG。对于电网强度对其他VSG并网构成系统小干扰稳定性的影响和相关稳定判据,将在后续发表的文章中作进一步报道。
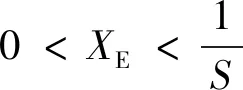
2.3 VSG并网系统小干扰稳定临界短路比
3 算例分析
3.1 算例1
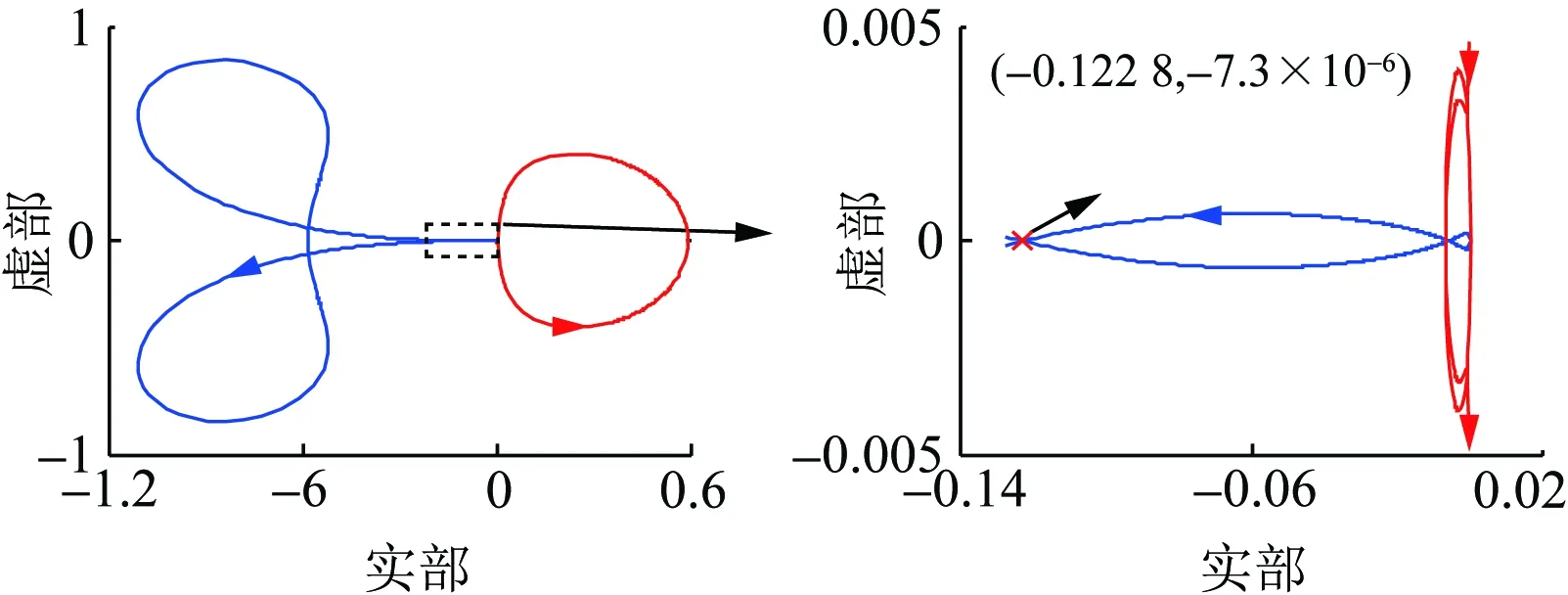


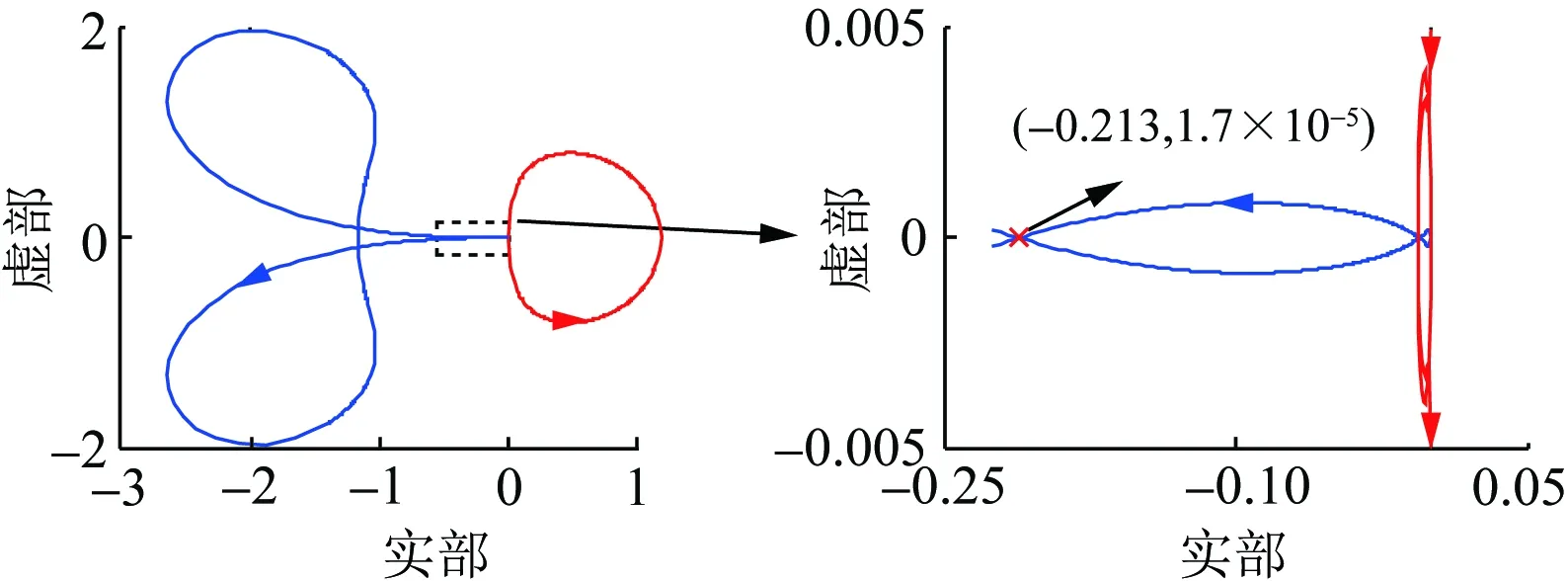

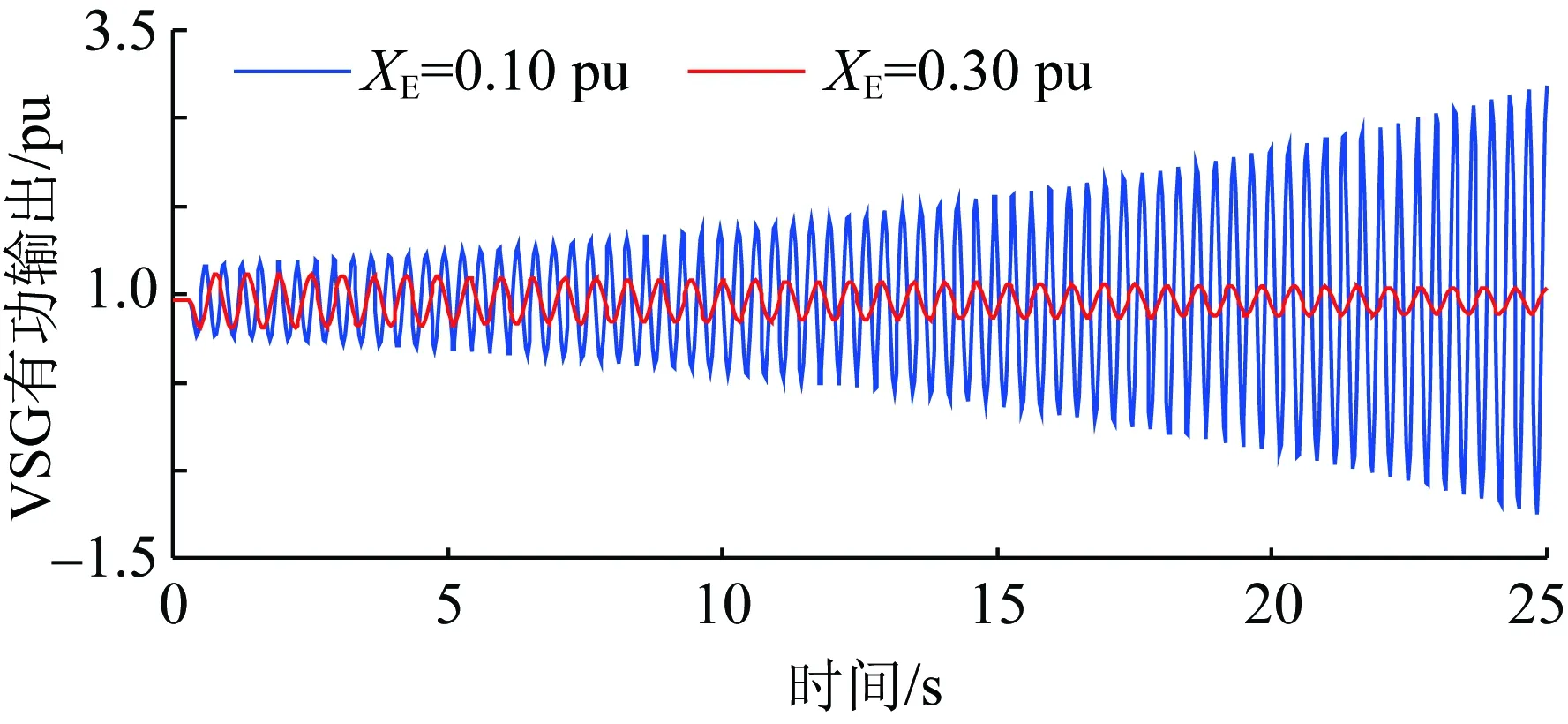
3.2 算例2
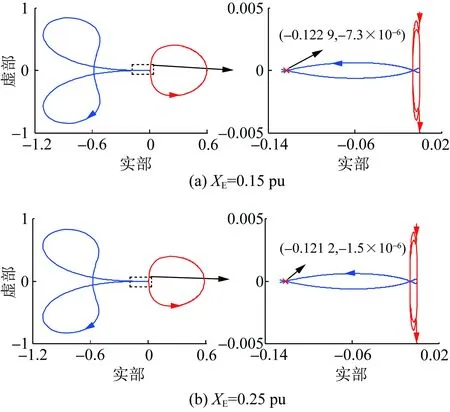


4 结 论
