融合注意力机制的输电线路故障概率预测模型
2022-03-18杨月孙博马晓忱罗雅迪孙英云
杨月,孙博,马晓忱,罗雅迪,孙英云
(1.华北电力大学电气与电子工程学院,北京市 102206;2.中国电力科学研究院有限公司,北京市 100192)
0 引 言
输电线路裸露在大气中,其运行状态直接受天气变化制约。近年来,极端气象灾害频发,高温热浪、低温冷害以及冰雪、台风等极端气候严重影响着电网安全[1-4]。2021年初,美国德克萨斯州电网受北极寒潮影响,发电机组因结冰而无法运转,电力供应急剧下降,造成严重的经济损失和社会影响[5]。因此,预测由天气导致的线路故障概率可以为电力部门提供预警参考,使其合理地制定线路防护和修复计划,保证电力系统的安全稳定运行[6]。现有的研究中,对输电线路故障进行预测大致可分为统计学方法[7-19]和人工智能类方法[20-25]。
统计学方法可分为参数模型[7-11]和非参数模型[12-19]两类。参数模型如傅里叶级数和泊松模型可以对气象信息和历史线路故障样本进行回归分析[7-8]。这种参数方法将故障发生的概率限制在给定的分布中,但线路故障发生概率遵循何种分布还未有定论。现有的研究为避免考虑故障概率的先验知识,给出了2种研究方法。一是忽略掉系统故障环节,直接将配电系统的可靠性建模为天气条件的直接函数[9-10],二是基于电力系统风险评估理论,选择描述模糊集合的函数来描述线路故障概率受气象因素的影响[11]。虽然一定程度减轻了先验知识的束缚,但本质上还是依赖给定函数对故障概率分布进行拟合。非参数模型包括马尔可夫模型、分位数法、区间法等,是一种基于数据但不依赖先验分布的方法。马尔可夫模型是建立气象与电网故障关系常用的一种非参数模型[12-14],有二态模型、三态、多态模型[15]和衍生模型[16]。马尔可夫模型假设状态变化的概率是固定的,缺乏对天气特征不确定性的考虑。天气特征具有天然的模糊性和不确定性,在对与天气相关输电线路故障进行精确概率预测时存在困难[17-18]。应用平均故障率和故障预测区间的模型则在一定程度上考虑了模型对气象不确定性。统计类方法中的非参数方法相较于参数类方法能在很大程度上减轻对故障先验分布知识的依赖,并且提高预测精度[19]。非参数法限制条件少、适应性广,但对于大样本数据,如若不采用适当的近似方法,将面临繁复的计算问题。
人工智能方法拥有强大的非线性表达能力,并且对噪声数据的容错性较强。文献[20-21]分别通过建立极限学习机(extreme learning machine,ELM)模型和融合注意力机制的自然语言处理网络来学习极端天气条件与给定分布参数之间的非线性关系,但模型有过拟合倾向,泛化能力较差。在机器学习算法中,以集成为基础的方法相较于单一的学习方法能提供更好的故障估计,并能利用模型优秀的泛化能力来应对过拟合问题[22-24]。这些模型仅建立起单一气象条件或极个别气象条件对线路故障的影响,实际并未考虑气象条件间复杂的相关性,忽略了其余潜在气象条件对电网故障的影响[23]。利用神经网络对概率进行非参数法的预测在气象相关故障的不确定性预测中有良好的表现。为了克制过拟合现象,并且考虑多种气象间的相关性,文献[25]基于贝叶斯神经网络(Bayesian neural network,BNN)建立了预测风、雨和闪电天气相关故障模型。该模型具有不确定性估计的能力,但BNN依靠输入气象信息的确定性有向图,无法发掘有向图外其他气象间的潜在联系。注意力机制则是一种能够依据输入间的相关性对输入序列进行权重分配的机制,在负荷的短期预测和风电出力的超短期预测中得到应用[26-28],而在气象相关故障概率预测中应用较少。引入注意力机制能发掘气象输入数据间的相关性,突出关键气象特征,提升预测精度。
综上,考虑到天气相关线路故障概率分布的未知性,非参数模型是研究该问题的有效工具。目前的人工智能方法利用多线程的集成学习来应对过拟合现象,但仍欠缺对气象条件间相关性以及气象条件不确定性的挖掘。多头注意力(multi-head attention,MHA)机制是一种通过多次并行计算注意力的概率分布,来量化每个输入对输出影响大小的神经网络结构[29],具有集成学习拥有的克服过拟合的优点,能够提炼多输入间的相关性并进行注意力权值分配,可用于提取输入气象间以及气象和故障概率间的相关性。本文研究的工作内容为分析气象相关输电线路典型故障的物理化学作用机理和统计特征,建立基于融合注意力机制的输电线路故障概率预测模型,并使用停电数据对模型进行检验,验证模型的有效性。
1 输电线路故障分析
1.1 气象因素对相关故障的影响
输电线路典型故障可大致分为机械类故障和绝缘类故障两类[30]。气象因素在输电线路故障成因中占比很高,其中风害、冰害、雷害是最为活跃的影响因子。
在常规的气象预报中,风的预报包括风向和风速2个特征,风向在一定程度上决定了输电塔迎风的受力面积,风速则决定了输电塔受风力破坏的大小。当风向与杆塔及导线构成了某些特殊角度,此段线路会因受较大的侧向风荷载的压迫,使塔底的承重超过设计的最大限值。风速越大,塔底受风的作用力越强。当作用力超过杆塔及线路的承受能力时,便会发生倒塔断线或杆塔倾斜事件。除上述机械故障外,风还会使线路发生风偏闪络、跳闸等绝缘性故障。
覆冰的形成与大气温度、湿度、风有关,在低温高湿的风口环境尤易形成。线路上的覆冰增加了导线(地线)开裂、杆塔变形、金具破损的可能性。在大风天气下,线路的不均匀覆冰会导致线路发生覆冰舞动、短路跳闸或更严重的短路烧伤事件。在温度升高时,若融冰过程中气温达不到使覆冰全部溶解的温度,融化的水和凝结的冰凌均会导致绝缘子的绝缘特性降低,增大绝缘性故障发生的可能。
雷电集中发生在湿度温度双高的环境中,此时云层形成的既快又厚,易产生雷电。相较于由风害和冰害导致的输电线路机械类故障,雷害导致的机械类故障通常是在发生绝缘类故障后,因绝缘损害导致金具遭到不可逆的破坏,而非使金具受到直接的机械性损害。
1.2 气象信息间的注意力关系
以上的分析表明,输电线路与天气有关的故障主要是由风害、覆冰以及雷电灾害造成的。形成这些气象灾害的基础气象条件间的物理化学作用机理复杂且难以量化,温度、湿度、风速、日照强度等基础气象条件的不同组合,可能会诱发不同的灾害气象。注意力机制可以选择性地关注部分输入数据,对样本中的不同特征赋予不同的权重分配,实现神经网络对输入特征的动态分析,并将加权求和后的信息输入神经网络学习,适于反映常规气象条件在极端气候形成时的权值。
多头注意力机制指在注意力机制的基础上进行多次并行运算,使网络能够从多维的角度挖掘相关性,集成单次注意力运算的拟合效果,能有效防止网络过拟合。因此,本文使用多头注意力机制来建立气象信息间的相互影响和气象信息对故障的影响。
2 考虑气象条件的输电线路故障概率深度预测模型
2.1 注意力机制
注意力机制的计算本质藏匿在查询Q、键K、值V三个向量中[31]。首先使用单个特征对应的查询向量Q和所有与该特征有相关的特征的键向量K进行相似度计算得到两者间相关性的权重值,反映各键向量对应的特征对查询向量Q所对应特征的影响大小。常用于计算Q、K间相关性权重值的函数有向量点积、矩阵转换、向量拼接等。接着使用softmax函数将计算所得权重映射到(0,1),令所有权值相加为1,并将权重和对应的每个特征的值向量相乘并求和,给出所有特征对该查询向量影响的概率乘性,以此得到当前查询向量的注意力值,如式(1)所示。在本模型中选用向量点积作为相似度计算函数,如式(2)所示。
(1)
f(Q,Ki)=QTKi
(2)
式中:fsoftmax(·)为softmax函数;Ki为第i个输入的键向量;Vi为第i个输入的值向量;f(·)为相似度函数。
注意力机制中,将查询向量来自某组输入本身,提取输入对象间相关性的方法称作自注意力机制。Q、K、V都是由原先的输入向量通过矩阵变换或网络变换得到的,如式(3)所示。Q向量最大限度地保留了输入本身的特点;K向量是为了区别于Q向量来放大输入数据间的异同,为计算各输入间相似度和相关性构建的向量;V向量与Q向量相似,用于反映输入的特征。在进行Q、K向量的相似度以及加权计算后,所得结果与V向量相乘即得最后自注意力机制的输出。
(3)
式中:X为输入向量,在本文中为由气象数据组成的向量X=[x1,x2,…,xn],其中xi(i=1,2,…,n)表示第i个气象特征,n为气象特征的个数;WQ为查询向量系数矩阵;WK为键向量系数矩阵;WV为值向量系数矩阵。
多头注意力机制通过将并行运算得出的D维结果拼接在一起,再由多头系数矩阵进行线性转换来从更多维的角度挖掘输入间的隐含关系,从而得到最终的多头注意力值。其表达式如式(4)所示:
(4)

2.2 故障概率预测模型注意力特征挖掘
在本文所提出的预测模型中,多头注意力运用在模型的2个部分。第1部分的输入是各类气象特征,称为MHA1层,其目的是建立各类气象特征间的相关性,输出隐含气象特征向量;第2部分的输入是MHA1层输出的各类隐含气象特征向量和故障特征向量,称为MHA2层,其目的是建立各类气象特征与故障特征间的相关性。
图1为MHA1层的示意图。输入的气象特征向量以自身的查询向量Q为基准,与其余气象特征的键向量K、值向量V进行注意力运算,并行进行N次运算后得到的隐含气象特征向量即为第一个多头注意力网络的输出。通过MHA1层,各类气象特征相互间复杂的物理化学作用机理被隐性地包含在隐含气象特征向量中。

图1 气象间注意力特征挖掘网络Fig.1 Inter-meteorological attention feature mining network
图2为MHA2层的示意图。隐含故障特征向量和总气象隐含向量进行水平拼接后得到上下文向量h′c,h′c以自身的查询向量Q为基准,与其余隐含气象特征向量的键向量K、V进行注意力运算。h′c作为既包含了气象特征也包含了故障特征的向量,在其余气象特征向量与其做注意力计算时能够反映各类气象特征对故障的影响程度,还能够让2倍维度的拼接向量回归隐含向量的维度大小。

图2 气象与故障间注意力特征挖掘网络Fig.2 Attentional feature mining network between meteorological and faults
MHA2层的输出作为单头注意力层的输入。数据在单头注意力层中并未进行完整的注意力机制运算,而只进行各隐含气象特征与上下文向量的相似度计算,表示各气象特征对故障特征的影响力大小,最终以softmax函数归一化处理后的数值作为各气象特征造成线路故障状态的概率值的大小。
2.3 故障概率预测模型网络结构
网络整体结构如图3所示,首先将预处理后的气象数据通过一个多头注意力层网络和一个前馈(feed forward,FF)层网络进行气象数据相关性的信息挖掘和维度扩充,并在这2层结构后分别增设残差归一化(add and norm,AN)层,该层的结构能够提升网络的训练效率,使气象信息在网络层传递时依旧保持良好的梯度传播功能,避免由于网络较深,而在传递过程中丢失最初网络气象输入的特征。
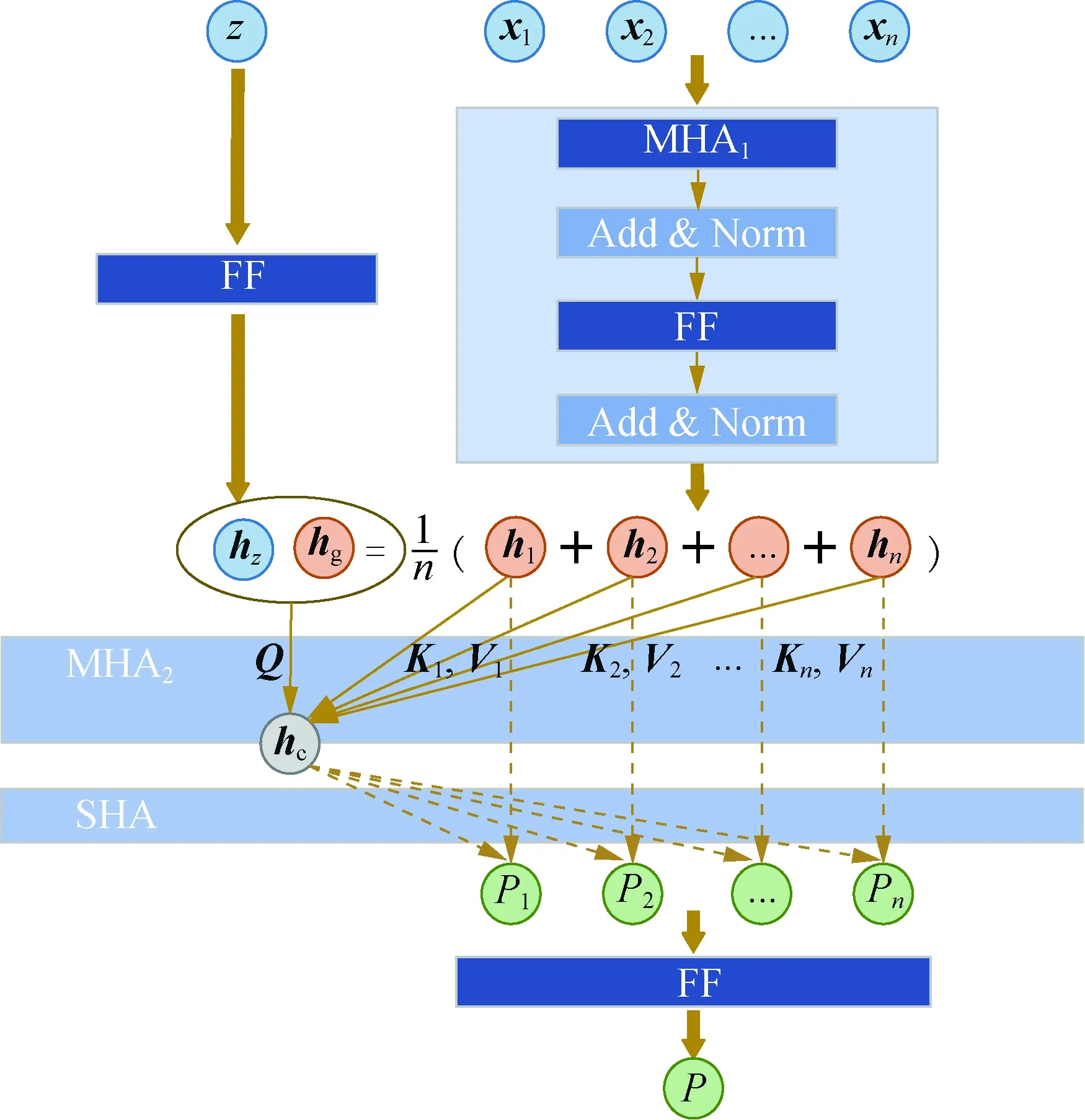
图3 故障概率预测网络总结构示意图Fig.3 Schematic diagram of total structure of fault probability prediction network
经过这4层网络结构后得到的向量称为隐含气象特征向量,其中包含了气象间相互影响,如式(5)所示。计算隐含气象特征向量的平均值,如式(6)所示,即得到包含所有气象特征的总气象隐含向量。
hi=fAN(fFF{fAN[fMHA1(Qi,K,V)]})
(5)
(6)
式中:Qi为第i个输入的查询向量;fMHA1(·)为多头注意力MHA1层过程函数;fAN(·)为残差归一化函数;fFF(·)为前馈层过程函数。
为了挖掘故障次数与气象数据间的关系,将故障数据z作为另一输入通过一个前馈层网络扩充其维度使其与隐含气象特征向量维度相同,得到的输出向量称为隐含故障特征向量,如式(7)所示。将隐含故障特征向量hz和总气象隐含向量hg进行水平拼接,得到包含气象及故障所有信息在内的上下文向量h′c,如式(8)所示。
hz=fFF(z)
(7)
h′c=[hz,hg]
(8)
在得到上下文向量后,将此向量再输入另一个多头注意力层MHA2。该层的目的与MHA1层并不同,MHA2层注重挖掘各隐含气象特征向量对拼接向量的影响程度,得到隐含拼接向量hc,如式(9)所示。此时的hc为将故障特征和气象特征纳入考虑的综合向量,其维度与隐含气象特征向量维度相同。
hc=fMHA2[h′c,(h1,…,hn)]
(9)
式中:fMHA2(·)表示多头注意力MHA2层过程函数。
在注意力机制的计算过程中,网络通过计算各输入相互间的权重并对输入加权求和得到输出,其中的权值代表输入间的影响力。为得到各气象特征在综合向量中的权重,在MHA2层后添加一个单头注意力(single-head attention,SHA)层来计算各隐含气象特征向量对隐含拼接向量hc的相似度,即各个气象因素对此次故障发生的影响占比,如式(10)所示:
Pi=fSHA(hc,hi)
(10)
式中:Pi表示第i个输入对应的故障概率;fSHA(·)表示单头注意力层过程函数。
最后,将各个气象特征造成故障发生的影响占比P1,…,Pn在前馈层网络中进行维度的伸缩变换,得到该气象特征下线路故障的概率,如式(11)所示:
P=fFF(P1,…,Pn)
(11)
本文所提出的预测模型中,用于深度拟合的前馈层有2个作用:一是对信息进行前馈传播,加深网络深度,增强网络的拟合能力;二是对信息进行维度变换,使网络最终输出单个故障概率值。
3 算例分析
3.1 数据集分析
停电算例数据来源于美国华盛顿州西雅图市,数据包括该市共5 664天的气象数据及对应天气下的线路停电次数,7个气象特征分别为日照长度、平均温度、平均湿度、最大风速、平均风速、最大阵风和降水。表1为因自然气象灾害影响导致的故障事件统计数据。

表1 算例数据统计Table 1 Case data statistics
如表1所示,该市受自然气象灾害影响较大,因天气条件发生的故障事件极多。发生1~3次停电事故和发生4次及以上停电事故的天数分别占数据总量的21%和48%。由于该市5 664天的电网停电数据相对来说数量较大,因此可先将此数据中正常、轻微故障事件(1~3次)及严重故障事件(4次及以上)发生的频率值近似看作概率值的先验,人为对该数据进行离散概率赋值。
3.2 气象和故障信息预处理
在神经网络训练中,若特征之间具有不同的值范围,不仅会使神经元的权重在不同的范围内波动,导致权值相乘时产生数值问题,还会使梯度在传播时发生梯度爆炸或消失等问题。因此,在数据输入网络之前需对数据进行归一化处理,以满足网络稳定求解的需要。
根据式(12)将原始的气象数据处理为标准正态分布的数据:
(12)
式中:μi为气象特征i的均值;σi为气象特征i的方差;x′i表示气象特征i归一化后的数值。
相较于将线路故障事件采用故障与否的二元分类的方法,根据输电线路历史运行数据将故障程度划分为3个区段能更直观地体现出线路故障程度。利用概率学中的大数定律,将每种事件发生的频率值Y1,Y2,Y3近似看作概率值的先验,人为对该数据进行离散的概率赋值。在发生的频率区间范围内进行随机赋值:
(13)
式中:ynormal为正常故障概率标签;yslight为轻微故障概率标签;ysevere为严重故障概率标签。
由此,每条日气象数据均在对应的频率区间内被赋予了故障概率标签值y。
3.3 输电线路故障概率预测
将5 664条日气象数据随机打乱后进行数据集分割,前4 000条气象故障数据作为该预测模型的训练集,后1 664条气象故障数据作为该预测模型的测试集,分别使用测试集和训练集计算模型的准确率。
通过对比预测网络模型的输出概率值所在的先验概率分布的三类区间(正常概率为0~0.31、轻微故障概率为0.31~0.52、严重故障概率0.52~1.00)与标签概率对应区间是否相同来判断预测结果是否相对准确,将判断准确的数据量占总体数据量大小的百分数作为模型的准确度。
采用BP网络与本文所提注意力机制模型做对比,所得损失值和准确率如表2和图4—6所示。从图4可知,BP网络与本文所提模型均能够有效收敛,但本文所提模型具有更好的收敛性。结合图5、6与表2可知,2种模型在训练收敛时对训练集均有较好的拟合能力。但在训练过程中,BP网络训练集准确度逐步上升时,测试集准确度出现下降趋势。这表明BP网络在训练收敛时存在严重的过拟合现象。而融合注意力机制网络训练准确度曲线和测试准确度曲线在训练中较为同步,具有更好的泛化性能。
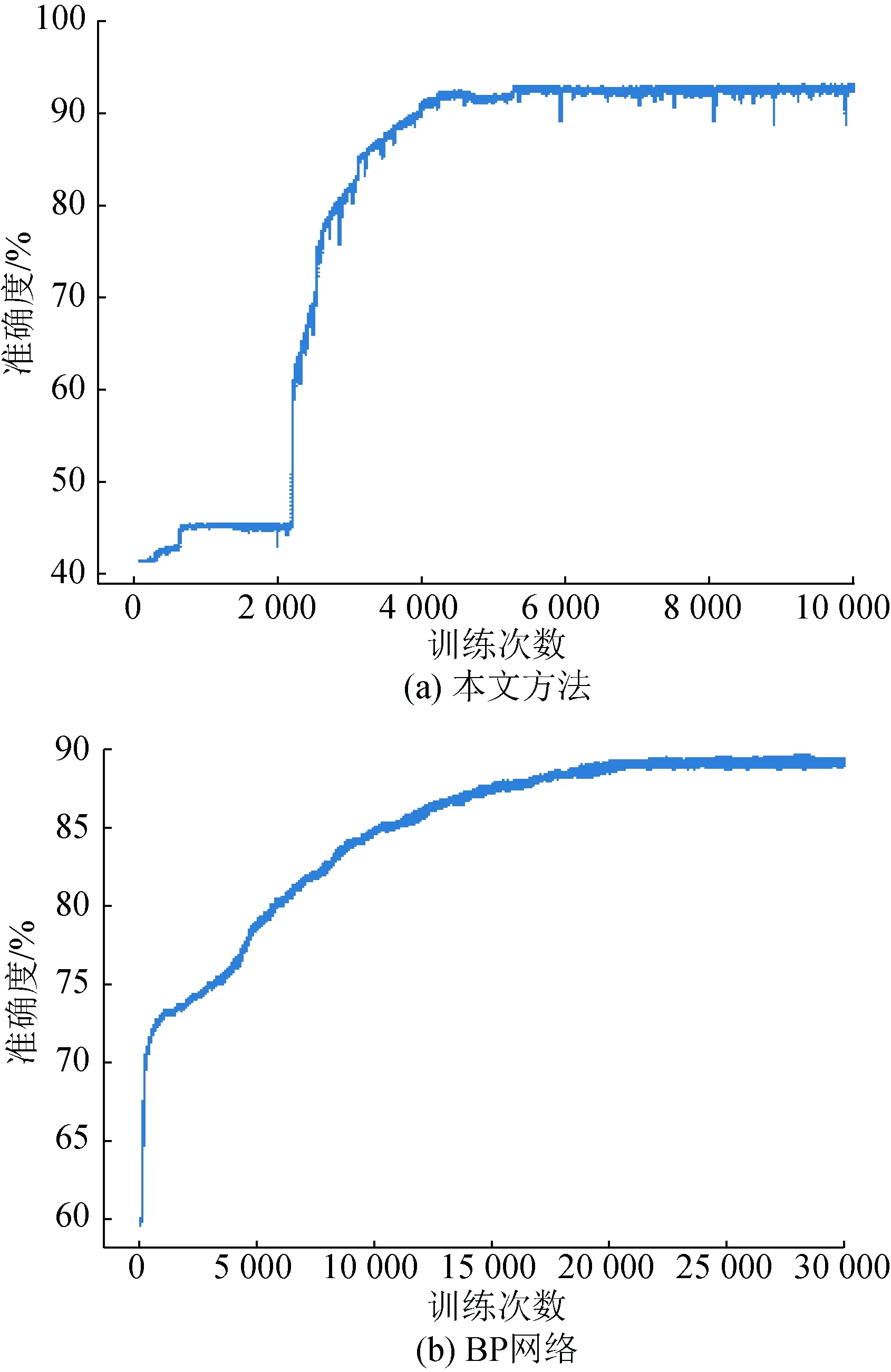
图5 本文网络与BP网络训练集准确度对比Fig.5 Comparison of the accuracy of the training set between the proposed network and BP network

表2 本文网络和BP网络效果对比Table 2 Effect comparison between the proposed network and BP network

图4 本文网络与BP网络训练损失对比Fig.4 Comparison of training loss between the proposed network and a BP neural network
表3提取了部分数据作为模型效果展示,前3条数据中日照强度相同,因第1天和第3天有降雨,对应日均湿度较第2天更大,日均气温更小。第2天的日最大阵风风速达到了23.9 m/s,达到9级风力,预测的故障概率值为41.7%,实际造成了电网1次故障。第3天日最大风速达到了17.1 m/s,达到7级风力,由于同时伴有低温和小雨,增大了输电线路特殊部分受风害及冰害的可能性,预测的故障概率为67.2%,实际造成了电网10次故障。同样,由于第5天的气象条件相较于第4天有更强的13级大风并伴有中雨,环境湿度更大,预测故障概率为42.8%,实际导致了西雅图市在当天共发生了2次停电故障。
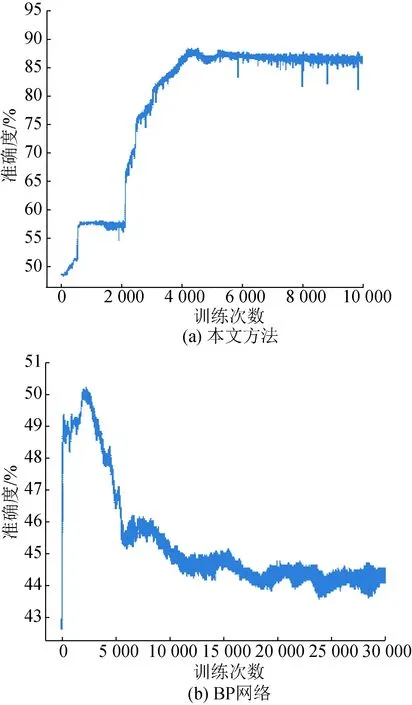
图6 本文网络与BP网络测试集准确度对比Fig.6 Comparison of the accuracy of the test set between the proposed network and BP network

表3 典型数据对比Table 3 Comparison of typical data
数据结果证明了该融合了注意力机制的神经网络模型在西雅图市算例中能对线路故障概率进行较准确的预测,可以为电力公司制定运维和修缮计划提供支持。
4 结 论
本文提出了一种融合注意力机制的线路故障概率预测模型,经过算例分析,可得以下结论:
1)相较于传统BP模型,注意力机制可以有效提取重要的特征信息,具有更好的预测精度与泛化能力;
2)相较于传统统计学模型,本文模型在进行概率预测时不依赖于对预测目标先验概率分布知识的掌握;
3)相较于对故障进行二元分类的分类模型,本文模型用概率值表示系统故障程度的大小能够提供更直观的预警信息。
此次工作依旧存在一些不足:本文对模型的参数解释不够,忽略了模型中注意力层的参数效果;数据集正常状态的样本较故障状态的样本更少,与实际中故障发生的频率存在一定差异,外推能力较弱。后续研究可以从以上所提缺陷出发,依次对模型进行修改与完善。
