双重耗能机制框架剪力墙结构地震响应分析
2022-03-18罗维刚刘纪斌宋江朋
罗维刚, 刘纪斌, 宋江朋, 祁 盼
(1.兰州理工大学 土木工程学院,兰州 730050;2.兰州理工大学 西部土木工程防灾减灾教育工程研究中心,兰州 730050;3.深圳市建筑设计研究总院有限公司,广东 深圳 518031)
摇摆墙是一种墙底具有特殊构造的墙体[1],墙底约束被放松,地震作用下可降低上部结构本身的延性需求和破坏,减小基础在倾覆力矩作用下的抗拉设计需求。Housner[2]发现水槽结构整体摇摆可免遭地震作用的破坏。Priestley等[3]通过一个摇摆结构模型进行振动台试验,验证了Housner摇摆结构减小地震响应的有效性。研究表明[4-7],框架-摇摆墙结构与传统框架结构相比楼层层间变形更趋均匀,可有效防止柱脚层屈服机制;吴守君等[8]进一步提出了框架-摇摆墙结构的分布参数模型。Midorikawa等[9-15]在摇摆墙体与基础之间设置耗能减震装置可有效减小结构的地震响应,并可抑制了高阶振型对结构响应的影响。
另一方面,Murase等[16-17]研究了一种新型的混合被动控制系统,即在基础隔震建筑物与自由墙体之间设置阻尼器,该结构系统对脉冲式和长持时地震动具有良好的抑制作用,且具有较高的冗余性和鲁棒性。
综上所述,本文提出了一种双重耗能的框架剪力墙结构体系,即利用水平地震作用下框架与剪力墙的“剪切型”和“弯曲型”不同变形模式,在框架与剪力墙之间设置耗能单元,同时在剪力墙底部也设置耗能单元形成可控摇摆剪力墙,通过调整匹配两种耗能单元技术参数,控制结构的动力属性,并实现减振控制和能量耗散,减小结构的地震动响应和抗震需求,以及实现遭受强震后结构功能可恢复,损伤单元可更换,快速恢复使用功能的需求。从而响应吕西林等[18]在第16届世界地震工程大会上对开发摇摆、自复位和可更换等多种技术组合使用的结构新体系提出的展望。
本文以兰州地区某六层传统混凝土框架剪力墙结构为例,进一步改进为双重耗能机制的框架剪力墙结构体系,采用ABAQUS软件建立2D有限元模型进行非线性动力时程分析,研究该新型结构体系在地震作用下的动力响应以及耗能减震机理。
1 分析模型建立
1.1 原型结构基本信息
原型结构取自兰州地区某六层钢筋混凝土框架剪力墙结构,平面布置如图1所示。结构首层层高为5.1 m,标准层层高为3.1 m;柱截面尺寸为700 mm×700 mm;梁截面尺寸为300 mm×500 mm;连梁截面尺寸为300 mm×750 mm;楼板厚度150 mm;设防烈度为8度,场地类别为II类,设计地震分组为第三组,设计基本地震加速度为0.3g,混凝土采用C35,钢筋采用HRB400。
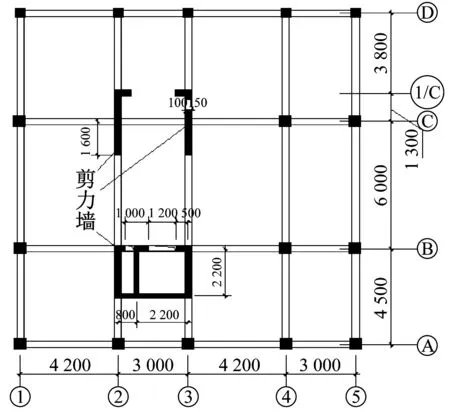
图1 框架剪力墙平面布置图
1.2 有限元模型建立
将原结构剪力墙按抗侧移刚度等效为一榀总剪力墙,并均匀分配至三榀框架结构,取其一榀利用ABAQUS建立2D有限元模型。考虑现浇楼板与配筋对框架梁的影响,以及减小高阶模态的干扰,保证框架结构以剪切型的第一阶模态振动,将有限元模型框架梁柱线刚度比取为10,以满足规范对刚性楼板的假定。本文通过保持梁截面尺寸不变,把梁的弹性模量放大来实现。楼板质量通过附加质量源分配至梁柱节点上。
有限元模型如图2所示,剪力墙等效厚度为250 mm,长度为4 m,用S4R壳单元模拟。框架梁、柱和连梁均采用B31纤维梁单元模拟。混凝土本构模型采用陆新征课题组开发并公开的PQ-Fiber材料库中忽略混凝土抗拉强度的模型Uconcrete01。框架剪力墙间的耗能单元采用防屈曲支撑(buckling-restrained brace, BRB),墙底耗能单元取金属阻尼器(metallic damper, MD),两种耗能单元具体参数设置与分布考虑如下。
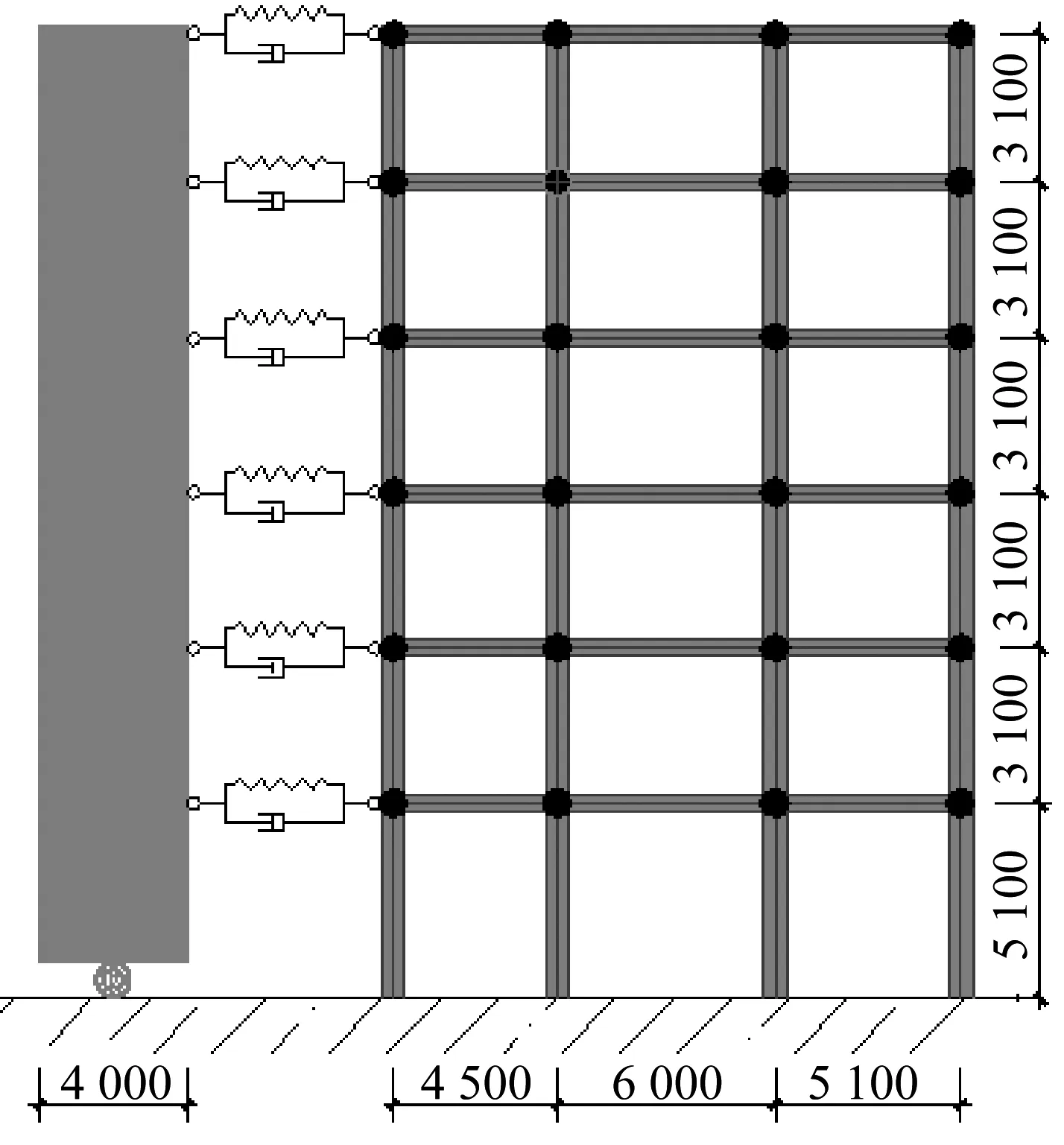
图2 结构分析模型
1.2.1 BRB参数设置与沿高度分布
BRB屈服强度取值和初始刚度参数沿高度设置,考虑了结构在水平地震作用下重力框架所产生的惯性力通过BRB传递于可控摇摆剪力墙,及考虑到新型结构体系抗震设计方法以传统框架剪力墙结构为基准进行的想法,将传统框架剪力墙结构在中震(0.3g)作用下动力时程分析获取的剪力墙基底剪力按倒三角沿结构高度分配至每层(与第一阶模态振动相匹配,已获得最大的效率),将每层获得的水平剪力作为该层BRB的屈服强度值,顶层标识为fy,其它各层从高到低沿高度成比例减小。为了便于初步分析,减小参数变量,BRB屈服变形暂取为0.003 5 m[19],由此求出各层BRB的初始刚度,亦成倒三角沿结构高度成比例变化。该模型可称为BRB基准模型。该基准模型顶层设置的BRB本构采用双线性随动硬化本构,如图3所示。参数包括屈服强度fy和初始刚度K0,而屈服后刚度K1取初始刚度的5%。

图3 基本模型中BRB本构关系
为了分析结构地震响应随BRB屈服强度的变化规律,本文建立了不同参数的BRB耗能单元框架剪力墙结构模型,即各模型顶层BRB屈服强度依次为0.1fy、0.3fy、0.5fy、0.7fy、0.9fy和fy,各模型其他层BRB亦与顶层按高度成比例关系,共计6个变化模型。取屈服强度比α为各模型与BRB基准模型屈服强度的比值,则α依次为0.1、0.3、0.5、0.7、0.9和1。
1.2.2 墙底MD参数设计
墙底耗能单元采用金属阻尼器(MD),用ABAQUS有限元中的非线性弹簧单元模拟。单元参数的选取考虑了混凝土剪力墙塑性铰区的抗倾覆承载能力和不同性能水准的塑性铰转动能力,即期望MD在小震时处于弹性阶段,而在中震(0.3g)时进入屈服。
(1) 剪力墙塑性铰区的抗倾覆承载力。为计算钢筋混凝土剪力墙塑性铰区的抗倾覆弯矩,需确定混凝土塑性铰区的高度lp,依据文献[20]
lp=(0.20+0.044H/h0)h0
(1)
式中:H为剪力墙总高度;h0为剪力墙截面宽度。
在本文传统框架剪力墙结构中剪力墙的剪跨比λ=1.28<1.5,参考文献[21]推荐的公式计算剪力墙底部塑性铰的抗剪承载力为V=1.7×106N,抗倾覆弯矩为Mu=Vlp=2.9×106N·m。
(2) 屈服转动角确定。参考FEMA356[22]给出的三个性能水平对应的剪力墙底部塑性铰转角值,如表1所示。墙底MD参数设置考虑在中震时屈服,取使用良好水平的塑性铰转角0.002 rad为MD屈服转角。

表1 不同性能水平的塑性铰转角限值
1.2.3 MD本构确定
基于结构在小震弹性,中震进入屈服的思路,MD本构选取为双线性随动强化模型,如图4所示。屈服后转动刚度取0.05。令Mu为防止倒塌水平抗倾覆弯矩,则使用良好水平的抗倾覆弯矩为MD的屈服弯矩My,即My=2×106N·m,计算弹簧转动初始刚度为C=1×109N·m/rad。该MD参数模型称为MD基准模型。
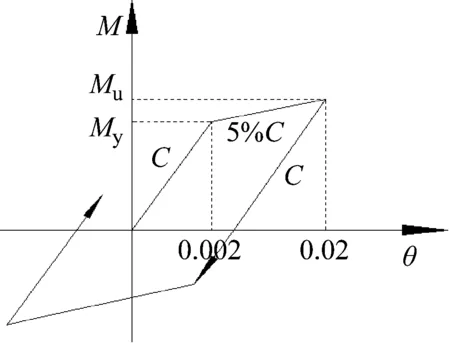
图4 MD本构关系
同样,为了研究结构地震响应随MD屈服弯矩与初始转动刚度变化的规律,建立不同MD参数的可控摇摆剪力墙模型,各模型MD初始刚度依次取为0(铰接),0.1C,0.5C,0.7C,C,3C,5C和10C,屈服转角不变,屈服弯矩与初始刚度等比例变化,共计8个变化模型。取转动刚度比β为各模型与MD基准模型转动刚度的比值,即β依次为0,0.1,0.5,0.7,1,3,5和10。
1.3 组合分析模型
框架与可控摇摆剪力墙之间连接BRB,同时在摇摆墙底部设置MD,以实现在地震作用下的双重耗能机制,两两组合建立了54个分析模型依次进行非线性动力时程分析,编号如表2所示。

表2 分析模型编号
2 地震波的选取
由于该双重耗能机制的框架摇摆墙结构为新型结构体系,地震动记录类型和数量的选取考虑了一定的统计特征,考虑地震动的类型、强度、持时、震中距和场地等因素,选取了9条天然波和3条人工波,如表3所示,并调幅至0.3g。图5为调幅后地震动加速度反应谱。
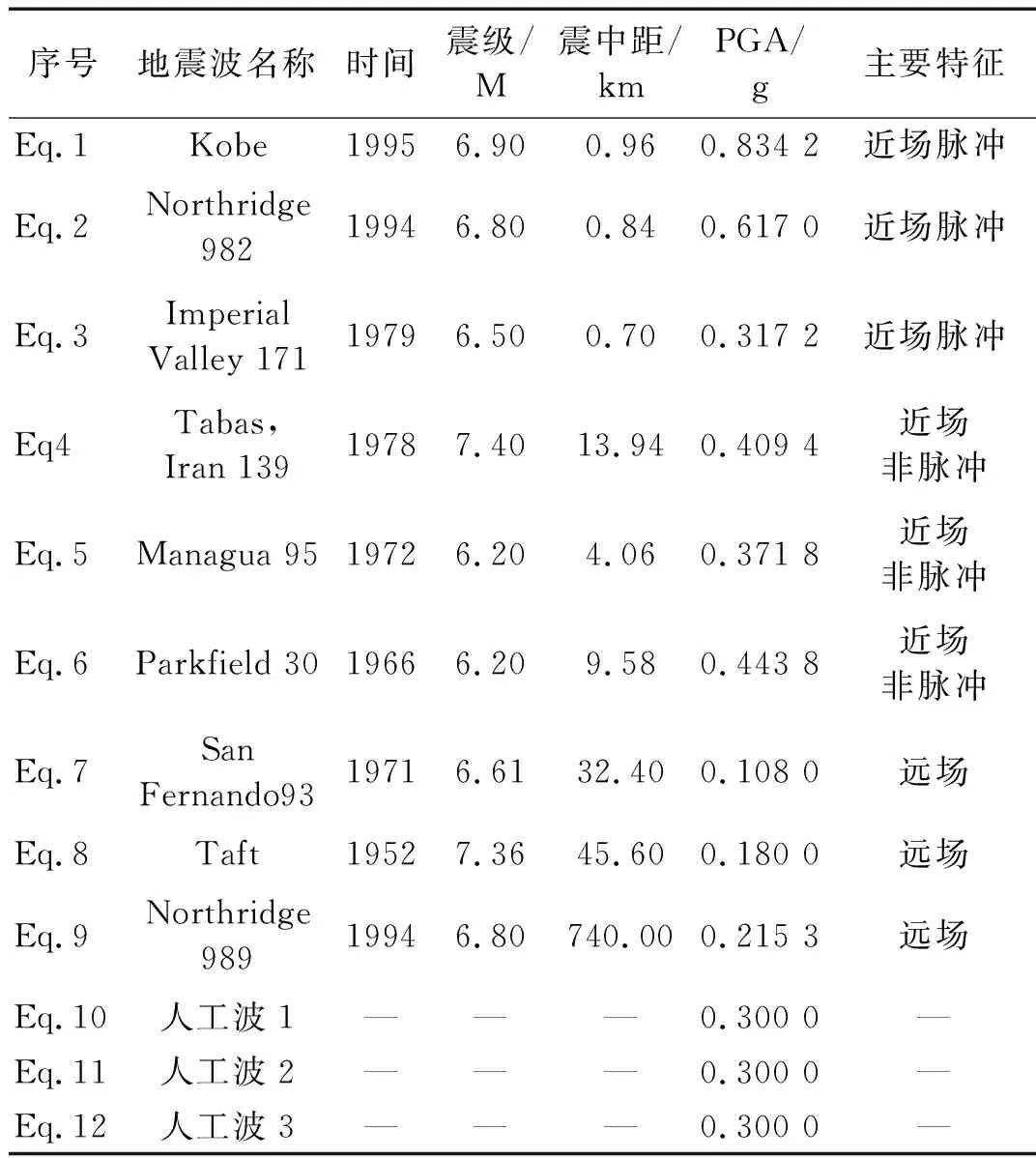
表3 地震动记录选取

图5 加速度反应谱
3 动力分析结果
分别对传统框架剪力墙结构与54个耗能结构进行非线性动力时程分析,讨论结构的侧向位移、峰值加速度、基底剪力、基底弯矩与框架侧向位移角等响应参数,分析BRB与MD两种耗能单元共同作用时整体结构的动力响应。便于分析讨论,各耗能结构各响应参数最大值均表达为与传统框架剪力墙结构对应数据的比值。
在以下绘制的三维视图中,BRB坐标轴表示为BRB屈服强度的变化。MD坐标轴表示墙底约束的变化,其中坐标轴刻度1表示为传统结构;刻度2表示剪力墙固接的单纯BRB耗能框架剪力墙结构;刻度为 3~10时,依次表示扭转刚度比β从0~10的结构。Z轴表示为耗能结构的各响应参数,为12条地震动记录计算获得最大值与原结构该响应最大值比值的平均值,此时原结构的地震响应均取为1。
3.1 结构框架侧向位移
双重耗能结构体系中框架顶点侧向位移随BRB和MD的变化如三维曲面图如图6所示,表明框架顶点侧向位移随BRB和MD的刚度变化呈现出高低起伏变化,当两者的刚度同时达到最大时,结构框架顶点侧向位移比传统结构大了21.2%;另外从图中可以看到三个深色区域,双重耗能结构响应比传统结构响应减小了25%左右,第一个出现在MD轴刻度为2的墙底固接单纯设置BRB,且BRB屈服强度在0.1fy~0.4fy之间变化的区域,因为此时墙底固接,说明仅依靠BRB耗能,双重耗能结构体系框架顶点侧向位移有所减小;其次MD坐标轴上刻度为4~7,即MD刚度在0.1C~1C变化,同时BRB屈服强度在0.1fy~0.3fy之间变化的区域;其三MD刚度在0.5C~1C(即图示中MD坐标轴5~7,以下均按MD刚度表述)变化且BRB在0.1fy~0.3fy之间变化时区域,后两个区域则是因为MD和BRB共同耗能协同作用引起的。三个区域中当MD为0.7C且BRB为0.7fy时框架结构顶点侧向位移相比原结构降低幅度最大,为36.3%。

(a) 主视图
3.2 结构框架顶点峰值加速度
双重耗能结构框架顶点峰值加速度的三维曲面图如图7所示。表明当MD坐标轴为2时的墙底固接单纯BRB耗能结构、坐标轴为3(β=0)的摇摆墙结构、坐标轴在4~8(MD在0.1C~5C)之间的MD耗能结构,当BRB在0.1fy~1fy之间变化时,峰值加速度均比传统结构减小20%以上。降低幅度达到了40%,主要分布在MD为0.1C~8C,且BRB在0.1fy~0.3fy之间。在这两个区域内框架顶点峰值加速度相比传统结构降低的最大幅度为54.7%。
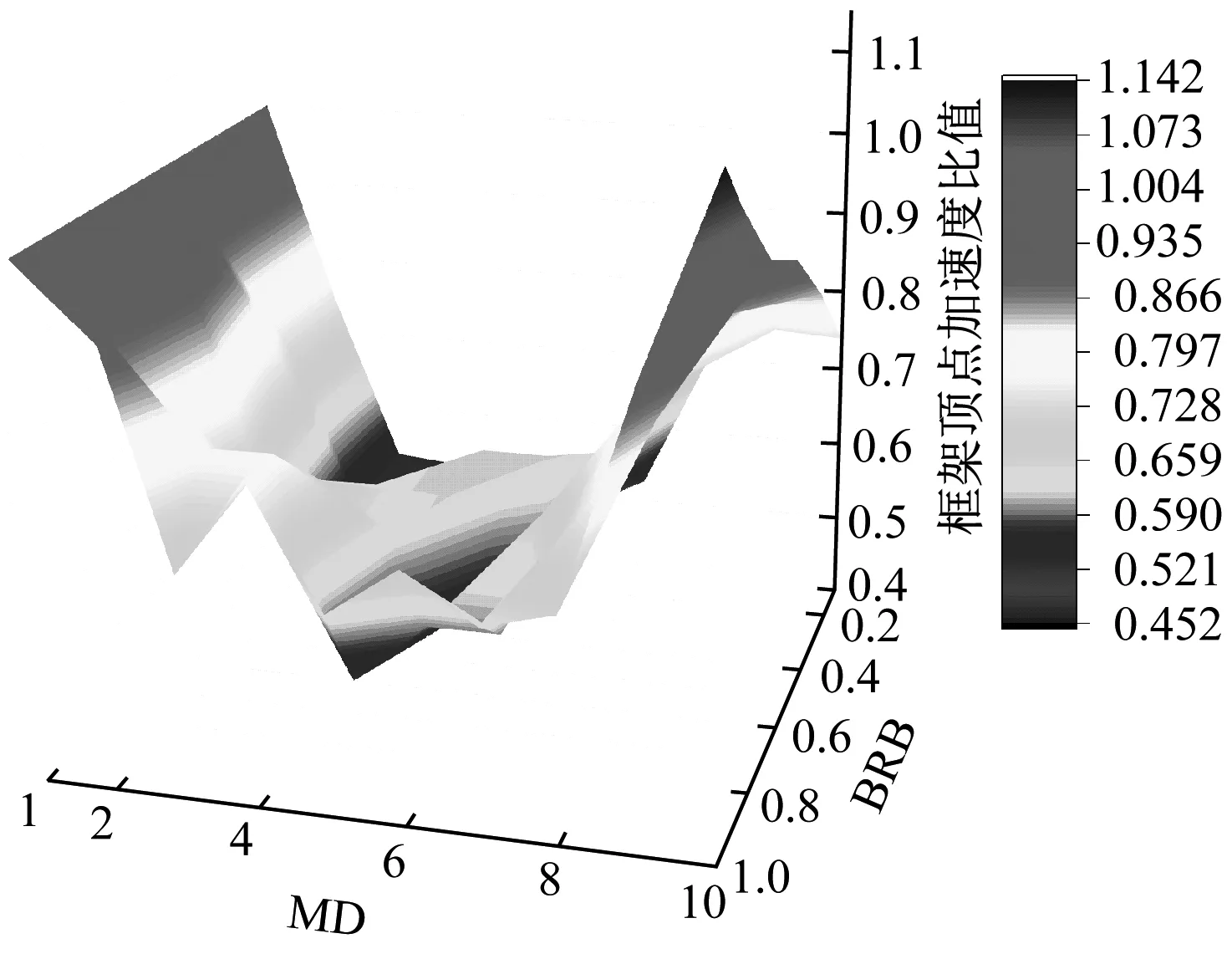
(a) 主视图
3.3 结构基底剪力
3.3.1 结构整体总基底剪力
如图8所示为双重耗能结构基底总剪力的三维曲面图,主视图中呈现出两边高中间低的一个凹槽状,主要分布在两个区域:一个是MD刚度在0~1C之间变化和BRB屈服强度在0.1fy~0.4fy变化形成的一个三角形区域;另一个是MD刚度在0.5C~1C变化和BRB在0.5fy~0.9fy变化形成的一个矩形区域,在这两个区域结构的基底总剪力相比传统结构平均降低了43.5%。此外,除了在BRB与MD参数均较大时的区域外,其他区域结构的基底总剪力也比传统结构有所降低,表明设置双重耗能单元的框架摇摆墙结构,MD和BRB的参数取值合理时,结构的基底剪力能够得到显著的降低。

(a) 主视图
3.3.2 摇摆墙基底剪力
如图9所示为墙底剪力三维曲面图,变化趋势和结构总基底剪力变化类似,但底部更为平滑,设置BRB的框架剪力墙双重结构由于BRB的切断机制,相比原结构的墙底剪力有所降低;在墙底完全铰接时,墙体基底剪力达到最小,随着MD的刚度增大,意味着逐渐限值墙体自由转动,故墙体的抗侧移刚度增大,在地震动作用下,剪力是按结构抗侧移刚度比分配的,因此墙体的剪力又增大了。在俯视图中则可以明显看到这些变化,墙体的剪力并不是只受MD刚度控制的,同时也受BRB参数的影响,在BRB强度比较小时,同样墙体剪力也小,这是由于BRB屈服强度小,地震作用下进入屈服状态耗散了地震能量,结构总剪力减小了,故墙体分配的剪力也相应减小。中间凹槽区域是BRB强度为0.1fy~1fy及MD刚度为0~1C形成的,剪力值相比较原结构下降了75%左右。
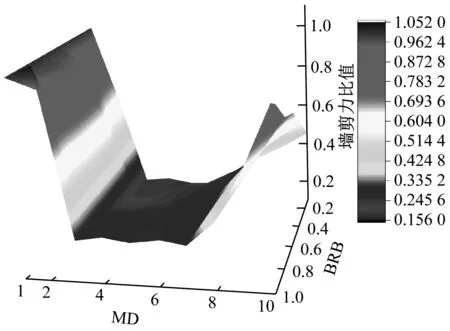
(a) 主视图
3.3.3 框架基底剪力
如图10所示为框架基底剪力三维曲面图,主视图相结合俯视图可以发现,所有工况的框架基底剪力值均小于原结构,但是由于耗能构件的参数属性不同,导致曲面呈现出锯齿状;MD刚度为0~0.1C及BRB强度为0.7fy~1fy时,框架基底剪力趋于原结构,分析可知此时MD的刚度过小,墙体接近自由摆动,同时BRB屈服强度过大,地震动下未能全部进入屈服状态,使得框架基底剪力增大;在MD刚度为5C~10C及BRB强度为0.5fy~1fy时,此时MD刚度和BRB的屈服强度过大,两个耗能构件未能全部进入屈服阶段,耗散的能量有限,使得框架柱基底剪力值趋于原结构。在其它区域,结构框架的基底剪力相比传统结构下降明显,最多下降达到了39%,且双重耗能单元相比单一耗能单元的框架摇摆墙结构的框架基底剪力更小。
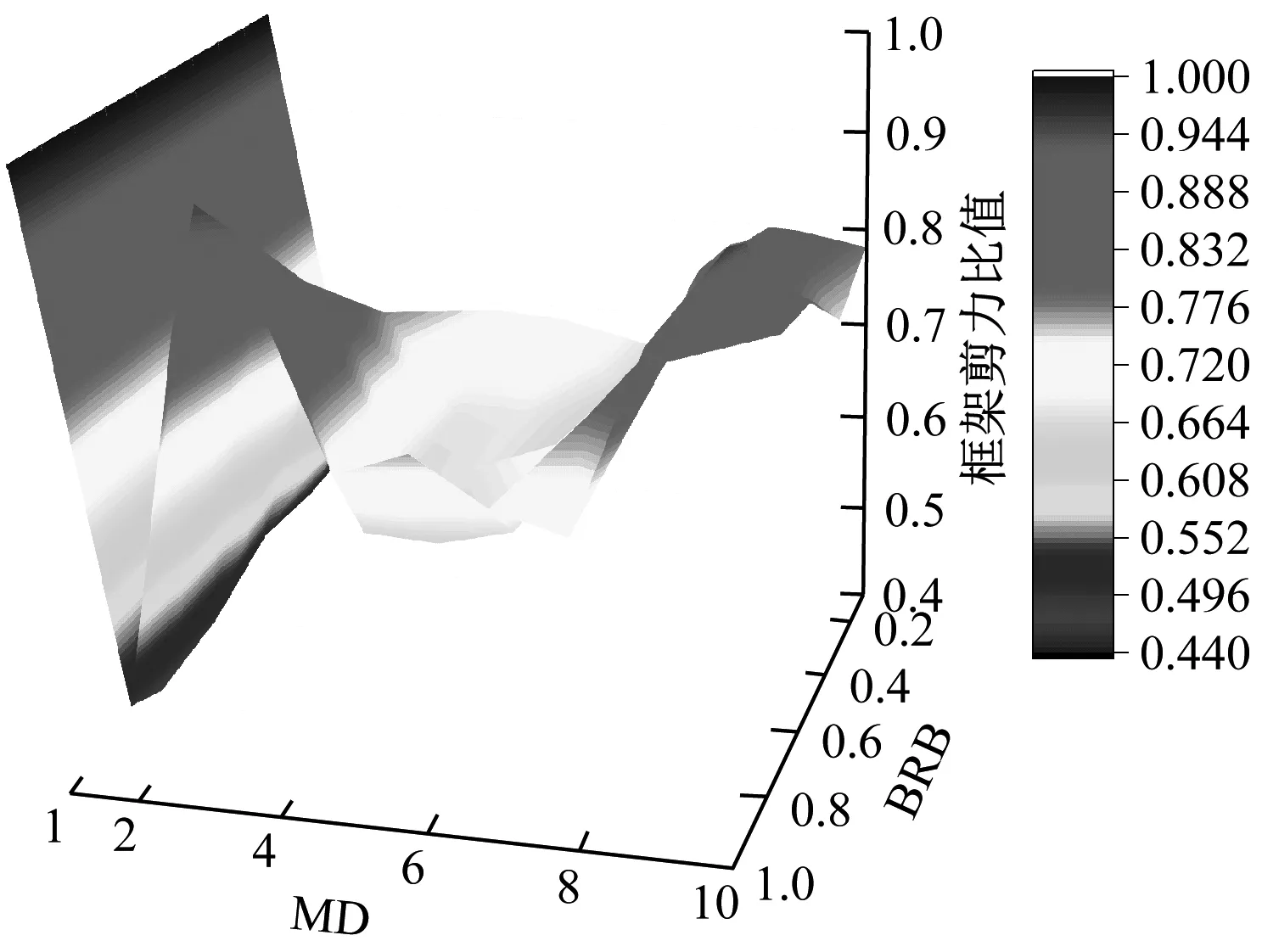
(a) 主视图
3.4 结构基底总弯矩
如图11所示为结构基底总弯矩的三维曲面图,从俯视图中观察到所有结构的基底总弯矩均小于传统结构,表明设置了耗能单元后,所有工况模型均能够降低结构的倾覆力矩;其次,在MD刚度为0时,BRB屈服强度为0.1fy~0.5fy时,有一个深色下凹区域,这是由于墙底完全铰接,墙底弯矩为0导致基底总弯矩下降比较多;此外MD刚度在0.5C~1C变化和BRB强度在0.5fy~0.9fy变化形成的一个深色的矩形区域,结构的基底弯矩相比传统结构也下降明显,由于MD和BRB协同作用共同耗能导致结构在此区域的基底弯矩显著降低,相比原结构最大降低了75.3%。
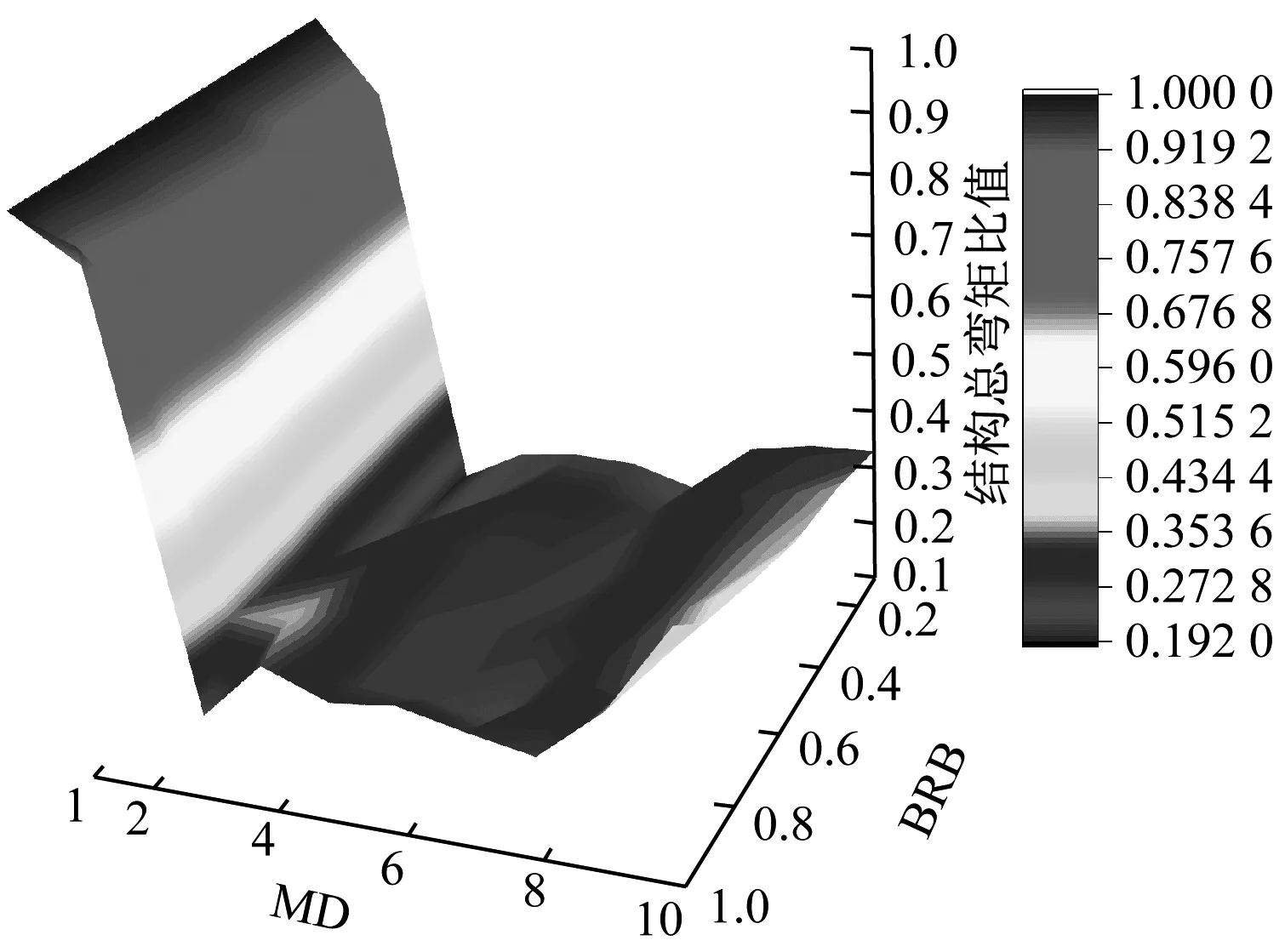
(a) 主视图
3.5 层间位移角分析
通过一系列动力响应分析结果得知,MD刚度在0.1C~1C之间和BRB强度在0.1fy~0.3fy之间变化形成的一个深色下凹三角形区域;以及MD刚度在0.5C~0.7C之间和BRB强度在0.7fy~0.9fy之间变化形成的一个深色下凹矩形区域,这两个区域范围内结构的各地震响应均最小。在这两个区域的工况一共有九个,其中在三角形区域内的有工况13、工况14、工况19、工况25及工况31,在矩形区域内的有工况22、工况23、工况28及工况29。
为分析在这两个区域内的结构层间位移角是否超过限值,现把以上九个工况的层间位移角和传统结构的层间位移角相对比,如图12所示,所有工况的层间位移角均优于原结构,尤其是原结构底层变形过大的缺点得到有效控制,设置双重耗能构件后的框架摇摆墙结构各层的层间变形趋于均匀,结构避免了薄弱层的产生。此外可以看到工况22及工况28的部分层间位移角超过了弹性限值,此时对应的BRB屈服强度均为0.7fy,两个工况均是在矩形区域内;其它工况均处于弹性层间位移角限值内,结构变形未进入塑性阶段,表明MD刚度在0.1C~1C之间和BRB强度在0.1fy~0.3fy之间变化形成的一个深色下凹三角形区域内的组合,框架摇摆墙结构的层间变形更加趋于均匀。
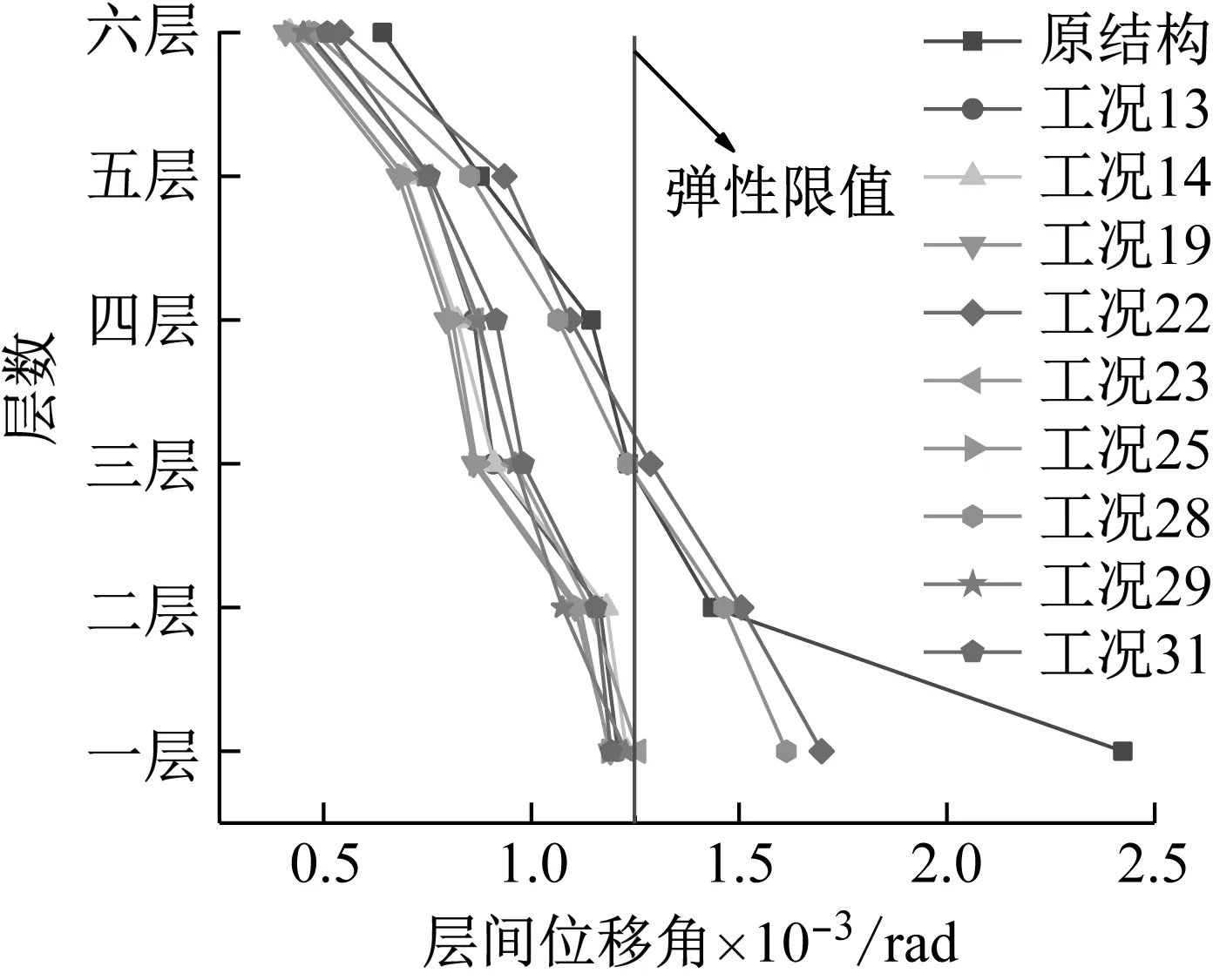
图12 不同工况层间位移角图
4 结 论
本文通过对一个六层框架剪力墙,设置不同屈服强度的BRB和不同刚度的墙底MD后,进行弹塑性动力时程分析,对比了各模型在地震动作用下结构地震响应,得到如下结论:
(1) 设置不同参数的MD和BRB的框架摇摆墙结构动力响应变异性增大,二者存在着相互耦联的作用,其中当MD刚度在0.1C~1C之间和BRB强度在0.1fy~0.3fy之间变化形成一个三角形区域内的最优区间时,双重耗能机制框架摇摆墙结构的动力响应减小,控制效果最好。
(2) 相比传统结构,MD和BRB的参数在最优的区间内时,结构框架顶点侧移下降了36.3%,框架顶点峰值加速度下降了54.7%,基底剪力下降了43.5%,基底弯矩下降了75.3%,可见双重耗能单元体系的框架摇摆墙结构的抗震需求明显减小。
(3) 本文通过变化不同刚度的MD及BBR组合,使得双重耗能机制的框架摇摆墙结构的抗震性能最优,但MD与BRB之间是如何协同作用的仍需进一步研究。
