理论设计ZnTiS3化合物光电性能的第一性原理计算
2022-03-18宁土荣周嘉欣凌诗武苏锟仁陈星源徐祥福林尔庆韩太坤祁玲敏赖国霞
宁土荣,周嘉欣,凌诗武,苏锟仁,陈星源,徐祥福,王 国,林尔庆,韩太坤,祁玲敏,赖国霞
(广东石油化工学院理学院,应用物理系,茂名 525000)
0 引 言
具有ABO3通式(A、B为金属阳离子)的金属氧化物钙钛矿通常是一种重要的铁电材料,常见的有BaTiO3、PbTiO3、BiFeO3和LiNbO3等。LiNbO3(LN)结构的铁电化合物,属于R3c空间群,而且绝大多数的LiNbO3型铁电化合物无法在温和条件下合成,需要高温高压的条件辅助[1-3]。LN-ZnSnO3(LN结构的ZnSnO3)由于较大的剩余极化强度,使其在应变传感器[4]、气体传感器[5-6]等领域有广阔的应用前景,但其禁带较宽,基本不吸收可见光。Kolb和Kolpak[7]通过把LN-ZnSnO3的O原子替换成S原子,设计出具有LiNbO3结构的铁电硫化物ZnSnS3,发现ZnSnS3的带隙直接由ZnSnO3的3.0 eV[8]降到1.3 eV,且其光伏特性也得到显著提高。与大多数ABO3型铁电氧化物一样,LN-ZnTiO3的带隙也较大,无论实验[9]还是理论计算[10-11],其禁带宽度均超过3 eV。LN-ZnTiO3和LN-ZnSnO3同属于R3c空间群材料,具有相似的结构和性质,其硫化物LN-ZnTiS3是否也具有较窄的带隙,可以使之成为潜在的光伏材料?本文通过第一性原理,计算LN-ZnTiO3及其对应硫化物LN-ZnTiS3的晶体结构、力学和电子性质,发现ZnTiS3满足力学稳定性条件,其带隙由于硫原子的替代得到降低,促进了可见光吸收,使其成为潜在的光伏材料。
1 理论模型与计算方法
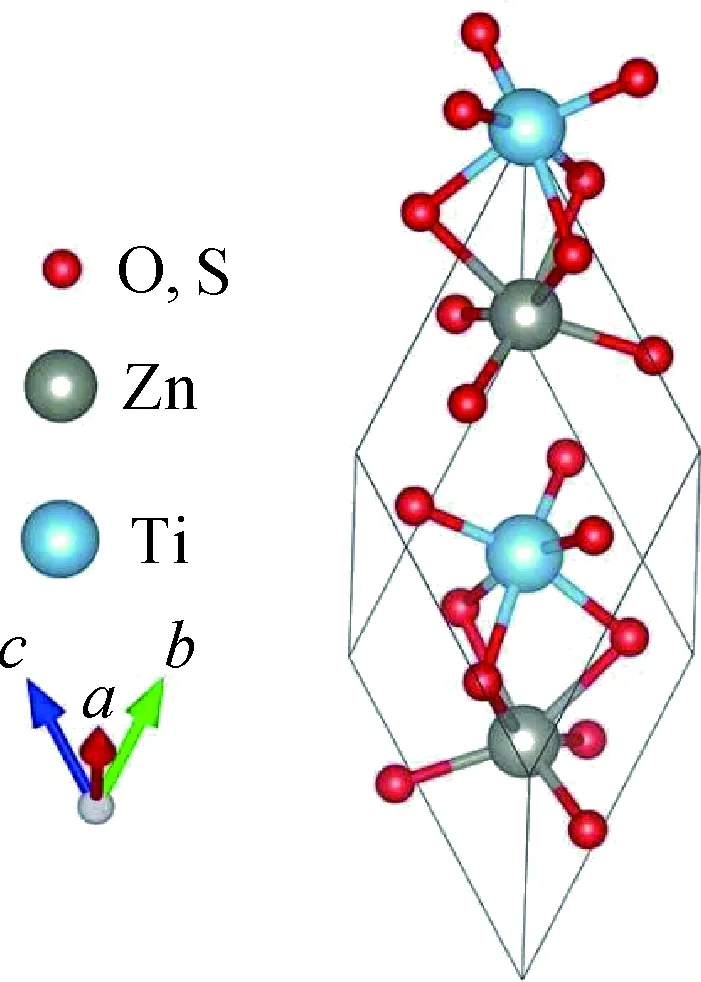
图1 LN-ZnTiO3型铁电氧化物及其硫化物的计算模型Fig.1 Calculation model of LN-ZnTiO3 type ferroelectric oxide and its sulfide
所有的计算均采用基于密度泛函理论赝势平面波ViennaAb-initioSimulation Package (VASP)[12-13]程序完成。采用投影缀加波(PAW)赝势[14]方法来描述电子与原子核之间的相互作用,电子与电子之间的交换关联泛函采用广义梯度近似(GGA)的Perdew-Burke-Ernzerhof (PBE)[15]来处理,PBE方法一般会低估材料的带隙,因此采用Modified Becke-Johnson (MBJ)[16-17]方法计算带隙和吸收光谱。LN-ZnTiO3体系和LN-ZnTiS3体系计算的平面波截断能分别取为520 eV和360 eV,布里渊区内的K点取样为0.3 nm-1。Zn、Ti、O、S的赝势分别取了d10p2、d3s1、s2p4和s2p4的外层价电子构型。电子迭代的收敛标准设为10-6eV,力的收敛判据设为0.1 eV/nm。计算的体系属于R3c空间群,模型含有10个原子,如图1所示。
表1为计算稳定结构的晶格常数及参考文献的计算值或实验值。对于LN-ZnTiO3铁电化合物,本文计算的晶格常数比实验值[3]大1.33%,与早期的理论计算结果接近[11],这证明了本研究方法的可靠性。

表1 LN-ZnTiO3型铁电氧化物及其硫化物晶格常数的计算值和实验值Table 1 Calculated and experimental values of lattice constants of LN-ZnTiO3 type ferroelectric oxide and its sulfide
2 结果与讨论
2.1 稳定性分析
弹性特性在材料科学、物理学、化学等领域是一个非常重要的研究对象,它与体系的各种物理特性有关,如状态方程、熔点、声子光谱等[18]。弹性常数Cij可以描述晶体的弹性性质,反映出晶体材料的刚度和稳定性。三角菱形晶体的弹性系数具有八个分量C11、C12、C13、C14、C33、C44、C65和C66。其中C65=C14,C66=1/2(C11-C12),因此,三角晶体实际上只有六个独立弹性系数[19]。表2列出了基于PAW-PBE方法计算钙钛矿LN- ZnTiO3及其硫化物LN-ZnTiS3的弹性系数。根据Born[20]准则,三角菱形晶体在零压下的力学稳定标准由不等式组(1)给出[20-21]:
(1)
表2中计算LN- ZnTiO3以及LN- ZnTiS3的弹性常数均满足不等式组(1),说明该体系满足力学稳定条件。

表2 LN- ZnTiO3型铁电氧化物及其硫化物弹性系数的计算值Table 2 Calculated elastic coefficients of LN-ZnTiO3 type ferroelectric oxide and its sulfide /GPa
三角菱形晶体的体积模量B和剪切模量G最大值可由Voigt[22]近似方法得到,其最小值则由Reuss[23]近似方法得到。Hill[24]认为应该把Voigt和Reuss近似方法的算术平均值作为估计多晶模量的标准值,提出了Voigt-Reuss-Hill近似,根据该近似得到LN-ZnTiO3与LN-ZnTiS3晶体材料的体积模量B、剪切模量G、杨氏模量E和泊松比ν等力学参数的计算值如表3所示。

表3 LN-ZnTiO3型铁电氧化物及其硫化物体积模量B、剪切模量G、杨氏模量E、泊松比v和B/G的计算值Table 3 Calculated bulk modulus B, shear modulus G, Young’s modulus E, Poisson ratio v and B/G of LN-ZnTiO3 typeferroelectric oxide and its sulfide
从表3数据可知,LN-ZnTiS3的体积模量B、剪切模量G、杨氏模量E计算数据均比LN-ZnTiO3小,说明其抗体积形变等能力比ZnTiO3弱,力学性能差。计算结果恰好表明氧原子的电负性比硫原子大这一事实。
根据Pugh[25]的相关理论,体积模量和剪切模量的比值B/G和泊松比ν是反映材料韧性或脆性的重要参数。计算结果表明,LN-ZnTiS3晶体材料具有较好的韧性和塑性。
LN-ZnTiS3的声子谱如图2(a)所示,该结构的声子谱没有任何虚频,进一步说明LN-ZnTiS3化合物是满足力学稳定条件的。

图2 第一性原理计算LN-ZnTiS3结构的声子谱(a)、与主要竞争相的平衡化学势相图(b)和不同压力下的形成焓(c)Fig.2 First-principles calculation of the phonon spectra of the LN-ZnTiS3 structure (a), equilibrium chemical potential phase diagram (b) and the formation enthalpy (c) under various pressure with its major competing phases
为了判断LN-ZnTiS3的热力学稳定性,计算了ZnTiS3的化学势平衡相图。表4给出了ZnTiS3及其主要竞争相的形成能计算值。要使得化合物ZnTiS3稳定存在,必须满足化学势的热力学平衡条件[26-27],依据这些条件,可以作出ZnTiS3体系稳定存在时的四面体相图,为直观起见, 将该四面体相图投影在ΔμZn、ΔμTi平面上, 投影是一个三角形,如图2(b)所示。
图2(b)显示ZnTiS3体系的相图没有稳定的化学势区域,说明常压下ZnTiS3很难在热平衡条件下稳定存在,表明合成ZnTiS3需要在高压的条件下进行。为此,计算了ZnTiS3与其主要竞争相在不同压力下的形成焓H=E0+PV,其中H和P分别代表形成焓和外部压力,E0和V是第一性原理计算零压下体系的能量和体积。计算结果显示,LN-ZnTiS3的相变压力出现在15.8 GPa处,表明当外部施加的压力大于15.8 GPa时,LN-ZnTiS3可以稳定形成。该方法计算类似体系LN-ZnXO3(X=Ge、Sn、Pb)在高压下的相变压力和实验趋势基本一致[2,28-30]。总的来说,化学势平衡相图和不同压力下的形成焓的计算结果表明,LN-ZnTiS3可以在高压条件下合成。

表4 ZnTiS3体系与其主要竞争相的单胞体积和形成能Table 4 Unit cell volume and formation energy of ZnTiS3 system and its major competing phases
2.2 能带与态密度分析
图3为用MBJ方法计算LN-ZnTiO3以及LN-ZnTiS3的能带结构图。图3(a)显示ZnTiO3的带隙为3.04 eV,与早期实验报道[9]和理论计算[11]数据接近,基本不吸收可见光。本文设计的LN-ZnTiS3,如图3(b)所示,其带隙计算结果为1.04 eV,说明硫原子替代LN-ZnTiO3的氧原子所形成的LN-ZnTiS3,能有效降低禁带宽度,促进体系电子的跃迁和可见光的吸收。
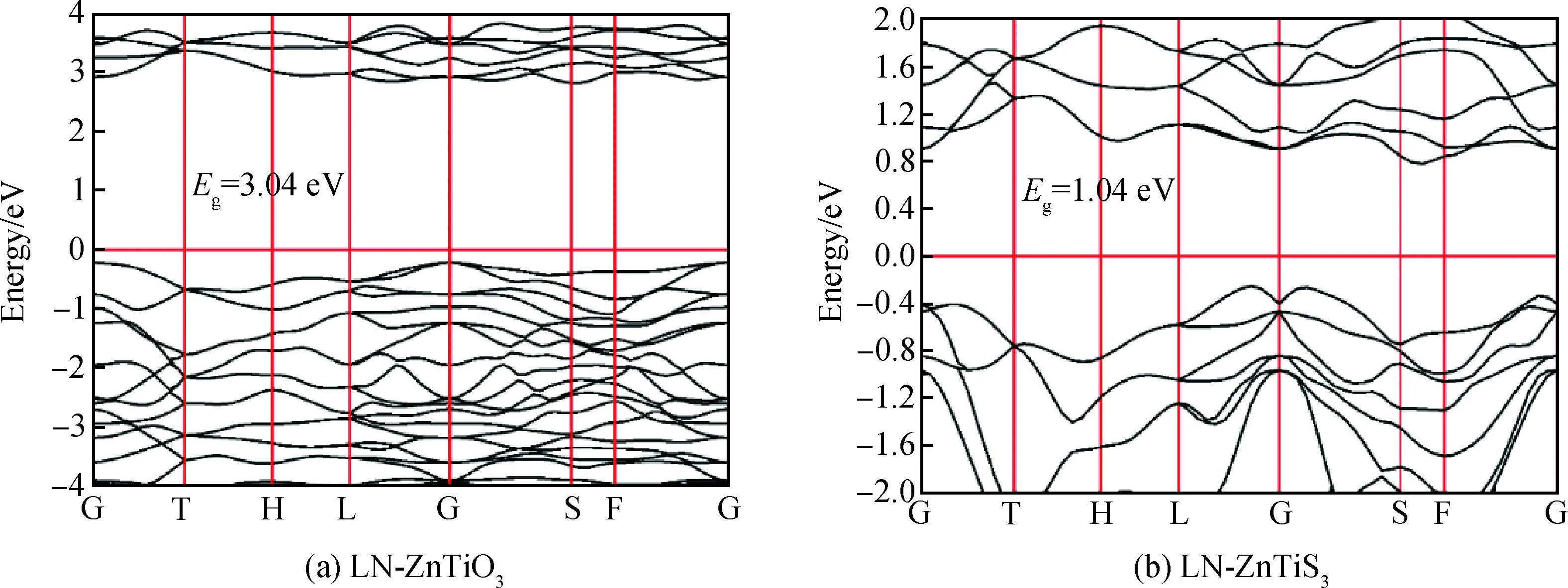
图3 LN-ZnTiO3 (a)和LN-ZnTiS3(b)铁电化合物能带结构理论计算Fig.3 Theoretical calculation of the band structure of LN-ZnTiO3 (a) and LN-ZnTiS3 (b) ferroelectric compounds
为了探究LN-ZnTiS3带隙降低的原因,计算了两种材料的分波态电子状态密度(PDOS),如图4所示。图4(a)LN-ZnTiO3的态密度显示,该体系价带顶(valence band maximum, VBM)的能级主要由O-p轨道组成,而导带底(conduction band minimum, CBM)则由Ti-d轨道组成,其轨道密度非常大,原因是Ti原子最外层的d轨道数目多,可容纳更多的电子。LN-ZnTiO3禁带宽度超过3 eV,使其难以对可见光产生响应。LN-ZnTiS3的态密度如图4(b)所示,VBM的能级主要由S-p轨道组成,而CBM则由Ti-d轨道组成。从图4(b)中可以看出,S与Ti在-2 eV到-3 eV有较强杂化,说明S与Ti充分成键,降低了Ti的非占据态能量,导带Ti-d轨道向低能级移动,从而降低LN-ZnTiS3的带隙,促进其对可见光的吸收。
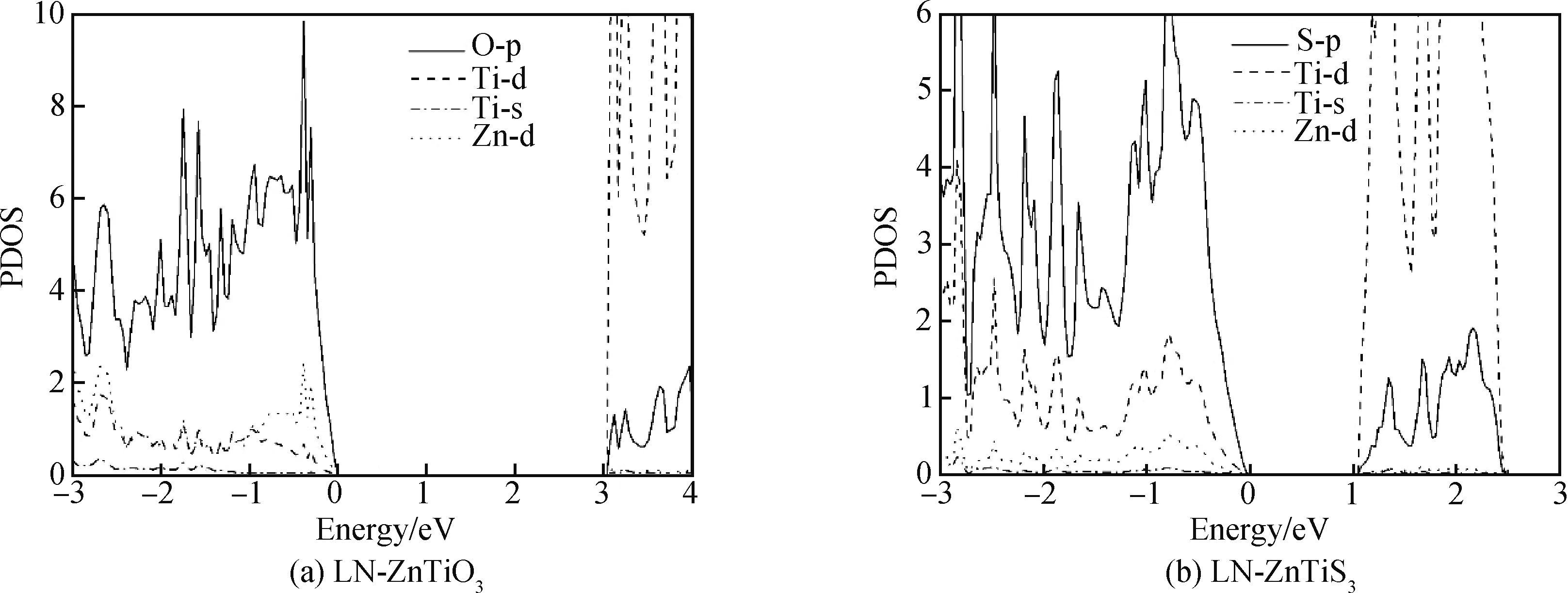
图4 LN-ZnTiO3 (a)和LN-ZnTiS3(b)铁电化合物态密度理论计算Fig.4 Theoretical calculation of the density of states of LN-ZnTiO3 (a) and LN-ZnTiS3 (b) ferroelectric compounds
2.3 光吸收性质分析
光波作为一种电磁波在介质中传播,当需要考虑吸收的影响时,用复介电函数ε(ω)[31]来描述。其表达式为:
ε(ω)=ε1(ω)+iε2(ω)
(2)
式中:ε2(ω)为虚部,由占据态与非占据态波函数矩阵元得到;ε1(ω)为实部,通过虚部ε2(ω)所满足的Kramers-Kronig关系[31]得到:
(3)
(4)
式中:p为积分的主值。光学吸收系数α(ω)与介电函数的关系由公式(5)给出[32]:
(5)

图5 ZnTiO3与ZnTiS3介电函数实部(a)、虚部(b)和吸收光谱(c)Fig.5 Real part (a), imaginary part (b) of the dielectric function and absorption spectra (c) of ZnTiO3 and ZnTiS3
图5(a)、(b)分别给出了ZnTiO3和ZnTiS3体系介电函数实部和虚部曲线,由图5(a)可知,ZnTiO3的介电常数为ε1(0)=5.426,ZnTiS3的介电常数增加到ε1(0)=12.948,相比于ZnTiO3,ZnTiS3的静态介电常数得到了极大提高,表明ZnTiS3的极化能力更强,硫原子的替代可以有效地改善ZnTiS3体系的光吸收特性。ZnTiS3两个主峰位于能量为1.360 eV和7.440 eV附近,ZnTiO3相较于ZnTiS3峰值有所减少。介电函数虚部反映了电子的跃迁能力,其峰值越大说明电子吸收能力越强。图5(b)显示,在光子低能区0~3.0 eV范围内,ZnTiS3的数值要远大于ZnTiO3,说明ZnTiS3材料对可见光区和红外光区光子的吸收能力要远强于ZnTiO3材料。介电函数的计算结果表明,ZnTiS3的实部和虚部均比ZnTiO3要大,ZnTiS3的光电性能优于ZnTiO3。
图5(c)表明, ZnTiO3在可见光的范围内吸收系数较小,而且增速平稳,直到入射光子的能量达到3.5 eV时,其吸收系数才急速增加,可见LN-ZnTiO3基本对可见光无响应。当入射光子的能量达到1.0 eV时,ZnTiS3的吸收系数就开始呈指数式增大,在可见光范围内,ZnTiS3的吸收系数明显比ZnTiO3大,说明硫原子的替代可以极大促进LN-ZnTiO3对可见光的吸收,与能带和态密度的计算结果相符合。
3 结 论
基于实验上已有的铁电材料LN-ZnTiO3,用第一性原理的方法设计了新型的铁电硫化物LN-ZnTiS3。计算结果表明LN-ZnTiS3化合物满足力学稳定条件。在化学势平衡相图计算中,发现LN-ZnTiS3在常压下不会形成稳定结构,但在外部超过15.8 GPa的高压下可以形成稳定结构。电子态密度和带隙的计算结果表明,LN-ZnTiS3的价带顶(VBM)主要由S-p轨道组成,导带底(CBM)则由Ti-d轨道组成,硫原子的替代可以促进体系费米能级以上的电子状态大幅度下降到较低的能级,从而降低LN-ZnTiS3的带隙,LN-ZnTiS3的带隙计算值为1.04 eV。在吸收光谱的计算中发现,当入射光子的能量达到1.0 eV时,LN-ZnTiS3的吸收系数就开始呈指数式增加,在可见光范围内,LN-ZnTiS3的吸收系数明显比LN-ZnTiO3大,与能带和态密度的计算结果相符合,相关的计算结果表明LN-ZnSnS3是潜在的高效率光伏材料。
